Python 中的图神经网络

介绍和分步实施

图机器学习领域近年来发展迅速，该领域的大多数模型都是用 Python 实现的。本文将介绍图作为一个概念以及一些使用 Python 处理它们的基本方法。之后，我们将创建一个图卷积网络，并让它在 PyTorch 的帮助下在现实世界的关系网络上执行节点分类。此处描述的整个工作流程可作为 Colab Notebook 使用。[0]

什么是图表？

图，在其最一般的形式中，只是节点的集合以及节点之间的一组边。形式上，图 G 可以写为 G = (V, E)，其中 V 表示节点，E 表示相应的边集。图有两种主要类型，有向图和无向图。有向图的边从原点 u 节点指向目标节点 v，而无向图中的边没有方向，使得 (u, v) ∈ E ⇔ (v, u) ∈ E。图可以通过邻接来表示矩阵 A. 这个矩阵可以通过让每个节点索引一个特定的行和列来创建。然后可以将边的存在表示为邻接矩阵中的条目，这意味着如果 (u, v) ∈ E 和 A[u, v] = 0，则 A[u, v] = 1，否则。如果图仅由无向边组成，则邻接矩阵将是对称的，但如果图是有向的，则不一定是这种情况。

为了在 Python 中操作图，我们将使用非常流行的 networkx 库 [1]。我们首先创建一个空的有向图 H：

import networkx as nxH = nx.DiGraph()

然后我们将向图中添加 4 个节点。每个节点都有 2 个附加功能，颜色和大小。机器学习问题中的图通常具有具有特征的节点，例如社交网络中人的姓名或年龄，然后模型可以使用这些特征来推断复杂的关系并进行预测。 Networkx 带有一个内置的实用程序函数，用于用节点作为列表填充图形，除了它们的特性：

H.add_nodes_from([
  (0, {"color": "gray", "size": 450}),
  (1, {"color": "yellow", "size": 700}),
  (2, {"color": "red", "size": 250}),
  (3, {"color": "pink", "size": 500})
])for node in H.nodes(data=True):
  print(node)> (0, {'color': 'gray', 'size': 450})
> (1, {'color': 'yellow', 'size': 700})
> (2, {'color': 'red', 'size': 250})
> (3, {'color': 'pink', 'size': 500})

图中的一条边定义为包含原点和目标节点的元组，例如边 (2, 3) 将节点 2 连接到节点 3。由于我们有一个有向图，因此也可以有一条边 (3, 2）它指向相反的方向。可以将多个边作为列表的一部分添加到图中，其方式与节点类似：

H.add_edges_from([
  (0, 1),
  (1, 2),
  (2, 0),
  (2, 3),
  (3, 2)
])print(H.edges())> [(0, 1), (1, 2), (2, 0), (2, 3), (3, 2)]

现在我们已经创建了一个图表，让我们定义一个函数来显示有关它的一些信息。我们验证该图确实是有向的，并且它具有正确数量的节点和边。

def print_graph_info(graph):
  print("Directed graph:", graph.is_directed())
  print("Number of nodes:", graph.number_of_nodes())
  print("Number of edges:", graph.number_of_edges())print_graph_info(H)> Directed graph: True
> Number of nodes: 4
> Number of edges: 5

绘制您正在使用的图表也很有帮助。这可以使用 nx.draw 来实现。我们使用节点的特征为每个节点着色，并在图中为每个节点赋予自己的大小。由于节点属性以字典的形式出现，并且 draw 函数只接受列表，我们必须先转换它们。结果图看起来应该有 4 个节点、5 条边和正确的节点特征。

node_colors = nx.get_node_attributes(H, "color").values()
colors = list(node_colors)node_sizes = nx.get_node_attributes(H, "size").values()
sizes = list(node_sizes)nx.draw(H, with_labels=True, node_color=colors, node_size=sizes)

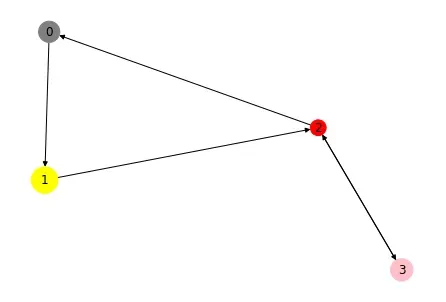
让我们将有向图 H 转换为无向图 G。之后我们再次打印有关该图的信息，我们可以看到转换成功，因为输出表明它不再是有向图了。

G = H.to_undirected()
print_graph_info(G)> Directed graph: False
> Number of nodes: 4
> Number of edges: 4

边缘的数量奇怪地减少了一个。如果我们仔细观察，我们可以看到边 (3, 2) 已经消失，这是合理的，因为无向边只能由一个元组表示，在这种情况下是 (2, 3)。

print(G.edges())> [(0, 1), (0, 2), (1, 2), (2, 3)]

当我们可视化无向图时，我们可以看到边的方向已经消失，而其他一切都保持不变。

nx.draw(G, with_labels=True, node_color=colors, node_size=sizes)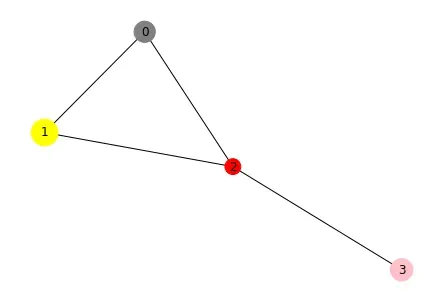

空手道俱乐部网络

现在我们已经对如何在 Python 中处理图有了更高层次的理解，我们将看看一个真实世界的网络，我们可以使用它来定义机器学习任务。为此选择了 Zachary 的空手道俱乐部网络 [2]。它代表了 W. Zachary 在七十年代研究的空手道俱乐部成员之间的友谊关系。如果两个人在俱乐部之外进行社交，则图中的一条边将他们连接起来。

空手道俱乐部数据集可通过 PyTorch Geometric (PyG) [3] 获得。 PyG 库包含用于对图和其他不规则结构进行深度学习的各种方法。我们首先检查数据集的一些属性。它似乎只包含一个图表，这是意料之中的，因为它描绘了一个俱乐部。此外，数据集中的每个节点都分配有一个 34 维特征向量，该向量唯一地表示每个节点。俱乐部的每个成员都是 4 个派系之一，或者机器学习术语中的课程。

from torch_geometric.datasets import KarateClubdataset = KarateClub()
print("Dataset:", dataset)
print("# Graphs:", len(dataset))
print("# Features:", dataset.num_features)
print("# Classes:", dataset.num_classes)> Dataset: KarateClub()
> # Graphs: 1
> # Features: 34
> # Classes: 4

我们可以进一步探索数据集中唯一的图。我们看到该图是无向的，它有 34 个节点，每个节点有 34 个特征，如前所述。边表示为元组，共有 156 个。然而，在 PyG 中，无向边表示为两个元组，每个方向一个元组，也称为双向，这意味着空手道俱乐部图中有 78 条独特的边。 PyG 只包含 A 中非零的条目，这就是为什么边这样表示的原因。这种类型的表示称为坐标格式，通常用于稀疏矩阵。每个节点都有一个标签 y，其中包含有关相应节点属于哪个类的信息。数据还包含一个 train_mask，其中包含我们在训练期间知道地面实况标签的节点的索引。有 4 个真值节点，每个派系一个，然后手头的任务是推断其余节点的派系。

data = dataset[0]print(data)
print("Training nodes:", data.train_mask.sum().item())
print("Is directed:", data.is_directed())> Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34])
> Training nodes: 4
> Is directed: False

我们将空手道俱乐部网络转换为 Networkx 图，这允许我们使用 nx.draw 函数对其进行可视化。节点根据它们所属的类别（或派别）进行着色。

from torch_geometric.utils import to_networkxG = to_networkx(data, to_undirected=True)
nx.draw(G, node_color=data.y, node_size=150)

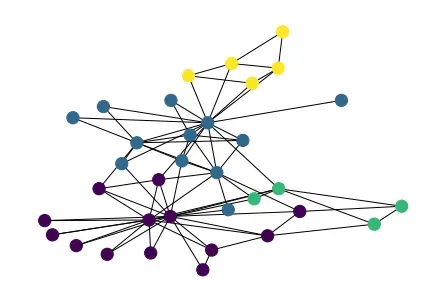
半监督节点分类

在训练模型以执行节点分类时，可以将其称为半监督机器学习，这是用于在训练期间结合标记和未标记数据的模型的通用术语。在节点分类的情况下，我们可以访问图中的所有节点，甚至是那些属于测试集的节点。唯一缺少的信息是测试节点的标签。

图卷积网络（GCN）将用于对测试集中的节点进行分类。做一个简单的理论介绍，图神经网络中的一个层可以写成一个非线性函数 f：

将图的邻接矩阵 A 和（潜在）节点特征 H 作为输入，用于某个层 l。图神经网络的简单逐层传播规则如下所示：

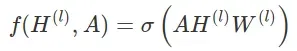
其中 W 是第 l 个神经网络层的权重矩阵，σ 是非线性激活函数。将权重与邻接矩阵相乘意味着对每个节点的所有（1 跳）相邻节点的所有特征向量进行求和和聚合。但是，不包括节点本身的特征向量。

为了解决这个问题，Kipf 和 Welling [4] 将单位矩阵添加到邻接矩阵并表示这个新矩阵 Â = A + I。邻接矩阵的乘法也会改变特征向量的尺度。为了抵消这个 Â 对称地乘以它的对角度矩阵，得到最终的 GCN 传播规则：

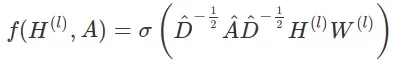
GCN 层已经是 PyG 的一部分，它可以很容易地作为 GCNConv 类导入。与在普通神经网络中可以堆叠层的方式相同，也可以堆叠多个 GCN 层。拥有 3 层 GCN 将导致三个连续的传播步骤，导致每个节点都使用 3 跳以外的信息进行更新。模型的第一层必须具有与每个节点具有的特征数量一样多的输入单元。根据原始 GCN 论文，潜在维度设置为 4，除了最后一个设置为 2。这允许我们稍后将学习到的潜在嵌入绘制为二维散点图，以查看模型是否设法学习属于同一类的节点的相似嵌入。双曲正切激活函数在 GCN 层之间用作非线性。输出层将二维节点嵌入映射到 4 个类中的 1 个。

from torch.nn import Linear
from torch_geometric.nn import GCNConvclass GCN(torch.nn.Module):
  def __init__(self):
    super(GCN, self).__init__()
    torch.manual_seed(42)
    self.conv1 = GCNConv(dataset.num_features, 4)
    self.conv2 = GCNConv(4, 4)
    self.conv3 = GCNConv(4, 2)
    self.classifier = Linear(2, dataset.num_classes)  def forward(self, x, edge_index):
    h = self.conv1(x, edge_index)
    h = h.tanh()
    h = self.conv2(h, edge_index)
    h = h.tanh()
    h = self.conv3(h, edge_index)
    h = h.tanh()
    out = self.classifier(h)
    return out, hmodel = GCN()
print(model)> GCN(
>   (conv1): GCNConv(34, 4)
>   (conv2): GCNConv(4, 4)
>   (conv3): GCNConv(4, 2)
>   (classifier): Linear(in_features=2, out_features=4, bias=True)
> )

我们使用交叉熵作为损失函数，因为它非常适合多类分类问题，并将 Adam 初始化为随机梯度优化器。我们创建了一个标准的 PyTorch 训练循环，并让它运行 300 个 epoch。请注意，虽然所有节点确实都对其节点嵌入进行了更新，但仅针对训练集中的节点计算损失。在训练过程中损失急剧减少，这意味着分类效果很好。来自最后一个 GCN 层的 2 维嵌入存储为一个列表，以便我们可以在训练期间动画嵌入的演变，从而深入了解模型的潜在空间。

criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)def train(data):
  optimizer.zero_grad()
  out, h = model(data.x, data.edge_index)
  loss = criterion(out[data.train_mask], data.y[data.train_mask])
  loss.backward()
  optimizer.step()
  return loss, hepochs = range(1, 301)
losses = []
embeddings = []for epoch in epochs:
  loss, h = train(data)
  losses.append(loss)
  embeddings.append(h)
  print(f"Epoch: {epoch}\tLoss: {loss:.4f}")> Epoch: 1    Loss: 1.399590
> Epoch: 2    Loss: 1.374863
> Epoch: 3    Loss: 1.354475
> ...
> Epoch: 299  Loss: 0.038314
> Epoch: 300  Loss: 0.038117

Matplotlib 可用于动画节点嵌入的散点图，其中每个点都根据它们所属的派系着色。对于每一帧，除了该时期的训练损失值外，我们还显示该时期。最后，动画被转换为下面可见的 GIF。

import matplotlib.animation as animationdef animate(i):
  ax.clear()
  h = embeddings[i]
  h = h.detach().numpy()
  ax.scatter(h[:, 0], h[:, 1], c=data.y, s=100)
  ax.set_title(f'Epoch: {epochs[i]}, Loss: {losses[i].item():.4f}')
  ax.set_xlim([-1.1, 1.1])
  ax.set_ylim([-1.1, 1.1])fig = plt.figure(figsize=(6, 6))
ax = plt.axes()
anim = animation.FuncAnimation(fig, animate, frames=epochs)
plt.show()gif_writer = animation.PillowWriter(fps=20)
anim.save('embeddings.gif', writer=gif_writer)

GCN 模型设法线性分离几乎所有不同类的节点。考虑到每个派系仅给出一个标记示例作为输入，这令人印象深刻。

希望您发现这个关于图神经网络的介绍很有趣。 GNN 是非常通用的算法，因为它们可以应用于复杂数据并解决不同类型的问题。例如，通过使用一些置换不变池（例如我们神经网络末端的均值）简单地聚合节点特征，它可以对整个图进行分类，而不是对单个节点进行分类！

[1] A. Hagberg、D. Schult 和 P. Swart，“使用 NetworkX 探索网络结构、动力学和功能”，SciPy2008，2008，networkx.org[0]

[2] W. Zachary，“小群体冲突和裂变的信息流模型”，J. Anthropol。水库，1977 年，doi：10.1086/jar.33.4.3629752[0]

[3] M. Fey 和 J. Lenssen，“使用 PyTorch Geometric 进行快速图形表示学习”，ICLR，2019 年，pyg.org，麻省理工学院许可证[0]

[4] T. Kipf 和 M. Welling，“图卷积网络的半监督分类”，ICLR，2016，arXiv：1609.02907[0]