ConvNext
1.drop path
1.1.复习下dropout
早些时候学习过drop out,先回顾下drop out的原理。
简单来说,就是在训练过程中随机“失活”部分神经元。,如图所示:
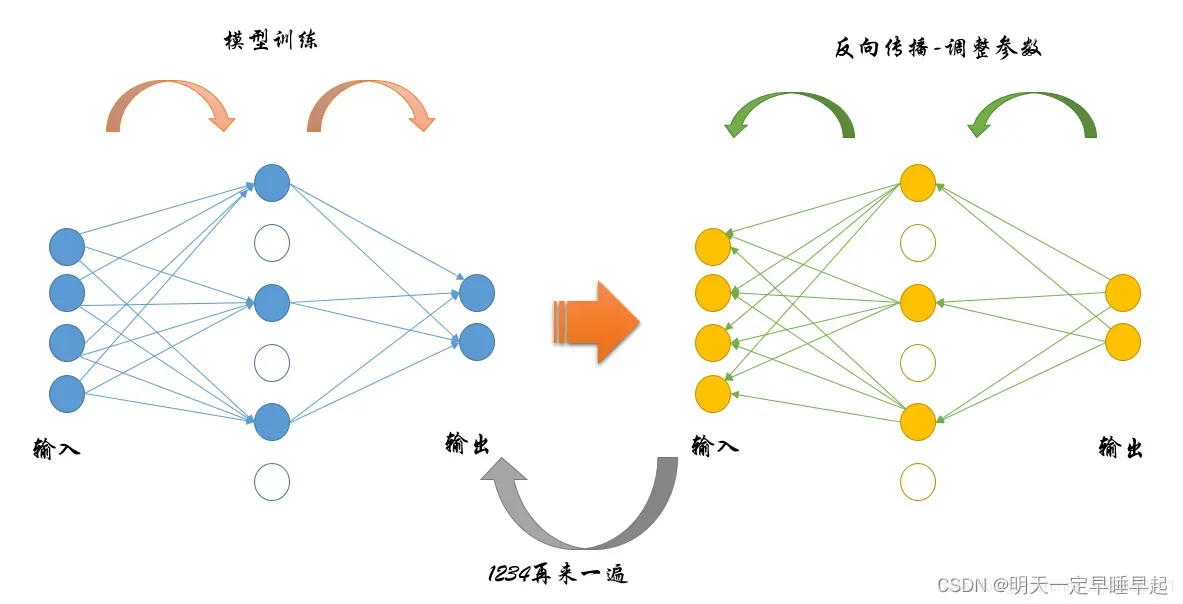
所谓失活,就是将神经元的输出值置0。
更具体来说,我们现在所用的dropout都是Inverted Dropout,即训练过程中除去失活的神经元外,对剩余的神经元进行缩放。
那么我们为什么要进行缩放呢?这就不得不提到早先时候dropout原始论文所提到的“朴素版”,也称为Vanilla Dropout
早先Vanilla Dropout,在训练的过程中不对剩余的神经元进行缩放,举个例子,我们假设在训练时输入以
的概率被丢弃,那么输入的期望就是
| x | 0 | |
|---|---|---|
| P | 1-p | p |
相当于训练的时候,我们输入的整体期望变小了。而如果在测试时我们不对输入x(假设这个输入x与训练时的输入x相同)也做对应缩放,会导致训练和测试输入的期望不一致,也就是说相同的输入在训练和测试时的输出可能不一致,这不是我们期望的。因此Vanilla Dropout会在测试时对输入进行
倍的系数缩放。此时测试输入的期望为
||(1-p)x|
|—|—|—|
|P|1|
可以看到,对测试输入也进行缩放后,训练与测试的输入总期望变一致了。但是这样做的一个问题是,测试过程需要根据训练过程进行调整,一不小心可能就会出错。
因此Inverted Dropout应运而生,只需要训练过程中除去失活的神经元外,对剩余的神经元进行缩放,在测试时无需根据训练过程进行调整。
那么我们该对剩余神经元缩放多少呢?回到我们的公式
我们的目的是,希望在测试时输入的期望与训练时输入的期望
相等。我们不希望对测试的输入做缩放,因此
,即我们希望在训练的时候使用dropout以后,仍有
观察上面两个公式,是不是知道已经该怎么做了?没错,就是在训练的时候对输入缩放倍。这时候你可能会有疑问:不是说只需要训练过程中除去失活的神经元外,对剩余的神经元进行缩放就可以了吗?为什么这里提到的对输入进行缩放就有一种对全部神经元进行缩放的意思呢?矛盾了吗?
其实并不矛盾,因为对神经元失活其实就是对神经元输出的值置0,我们对0进行缩放得到的结果仍然是0。所以,Inverted Dropout所描述的训练过程中除去失活的神经元外,对剩余的神经元进行缩放其实也可以理解成训练过程中对所有神经元进行缩放。
公式推导如下
小结一下,dropout就是按概率p失活部分神经元,同时对剩余的神经元进行缩放。
1.2.回到droppath
那么,什么是droppath呢?这里引用视频10.1 EfficientNetV2网络详解中21:21的讲解图
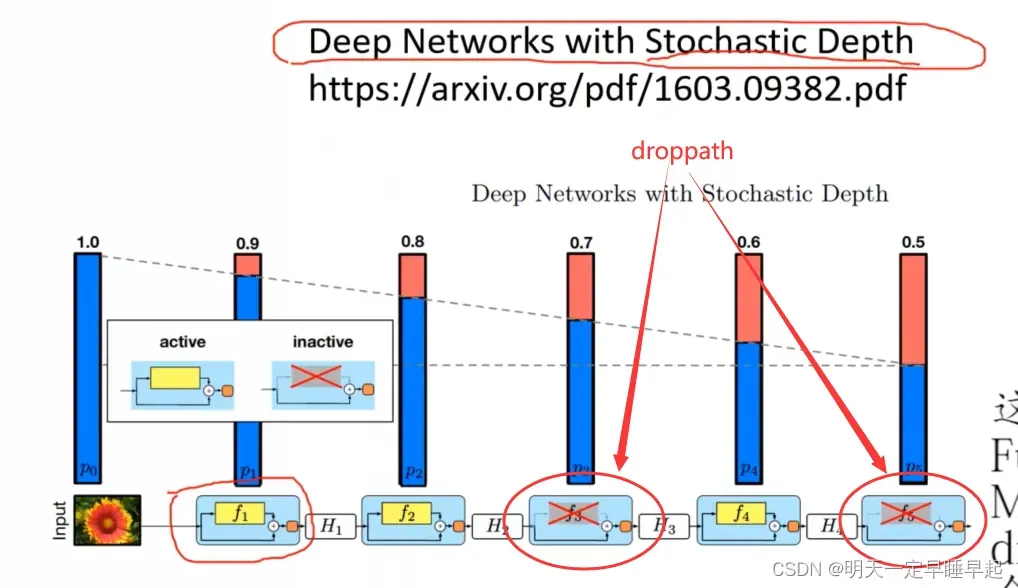
droppath出自论文《Deep Networks with Stochastic Depth》,其效果是将深度学习模型中的多分支结构随机“删除”,如图中红色圈出的打叉的部分所示,由于分支被删除,因而网络的层数也就减少,也就达到了论文所提到的Stochastic Depth(随机深度)的目的。
droppath与dropout的操作类似,都是先删除(失活)某一部分,再对剩余部分进行缩放。
1.3.源码实现及比较
1.3.1.dropout
接下来我们从代码层面讲解droppath的实现以及dropath和dropout的区别。
我们首先来看dropout的代码,这里引用视频15、Dropout原理以及其TF/Torch/Numpy源码实现中25:41秒开始的内容,如图所示
由于dropout的底层实现比较复杂,这里只是粗略的讲解下dropout的代码(C++实现)
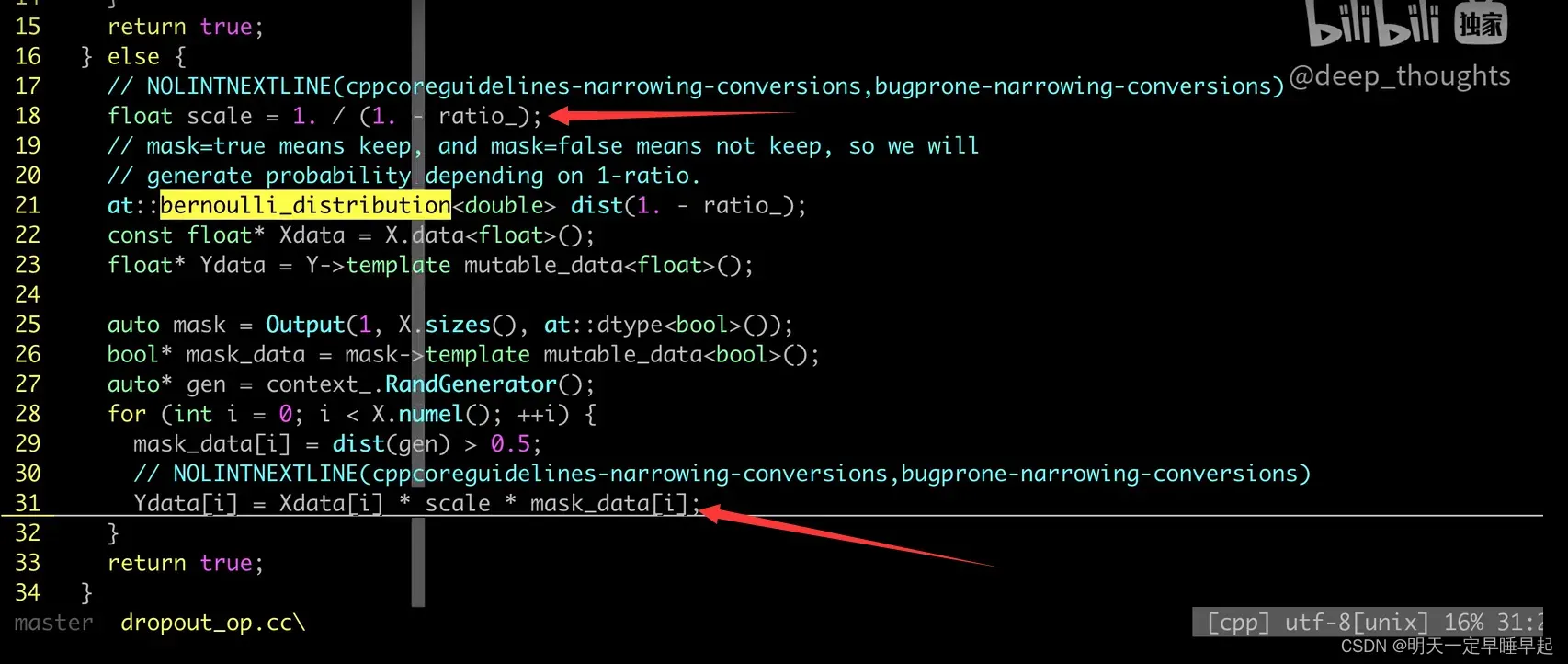
重点关注箭头所指的部分,Xdata表示输入矩阵,就是drop的概率,
就是我们要对输入进行缩放的比例。mask_data我们可以理解成一个仅由0和1组成且与Xdata的shape一样的矩阵。Xdata和mask_data的相乘我们可以理解成矩阵对应位置的元素相乘,这样我们就保留了Xdata中的部分元素。于是就得到了输出矩阵Ydata。dropout的原理大致如上。
1.3.2.droppath
droppath的python实现如下:
def drop_path(x, drop_prob: float = 0., training: bool = False):
"""Drop paths (Stochastic Depth) per sample (when applied in main path of residual blocks).
This is the same as the DropConnect impl I created for EfficientNet, etc networks, however,
the original name is misleading as 'Drop Connect' is a different form of dropout in a separate paper...
See discussion: https://github.com/tensorflow/tpu/issues/494#issuecomment-532968956 ... I've opted for
changing the layer and argument names to 'drop path' rather than mix DropConnect as a layer name and use
'survival rate' as the argument.
"""
if drop_prob == 0. or not training:
return x
keep_prob = 1 - drop_prob
shape = (x.shape[0],) + (1,) * (x.ndim - 1) # work with diff dim tensors, not just 2D ConvNets
random_tensor = keep_prob + torch.rand(shape, dtype=x.dtype, device=x.device)
random_tensor.floor_() # binarize
output = x.div(keep_prob) * random_tensor
return output
参数含义如下:
- x:输入,第一个维度通常表示batchsize
- drop_prob:以概率p删除分支
- training:判断模型是训练模式还是推理模式
我们重点关注前两个参数,首先x表示输入,通常第一个维度是batchsize,例如[B,C,H,W]或者[B,N,C]等。第二个参数表示按概率p执行删除分支。由于pytorch当中模型存在train模式和eval模型,这两个模式会改变nn.Module中的training属性,而pytorch中的Droppath类继承自nn.Module,前向计算函数当中调用的就是drop_path函数,因此第三个参数其实是跟着模型的模式走的,也就是说,当你的模型设置为train模式时,这个参数自动为True,设置为eval时为False。
首先我们对输入的drop_prob进行判断,如果drop_prob等于0,我们就直接返回输入x,如果模型处于eval模式,我们也会直接返回输入x,这点和Inverted Dropout是类似的。
接下来我们计算缩放系数keep_prob,后面我们对输入进行缩放时会用到它。
我们需要定义一个shape变量,它的值只保留batchsize维度,其它值均为1,这是为了在batchsize维度上与输入进行对应位置运算。
使用均匀分布生成一个范围在0-1之间的随机数,shape使用我们上面计算得到的shape。加上keep_prob得到random_tensor。
对random_tensor进行向下取整,因为keep_prob和我们均匀分布随机生成的数范围都在0-1之间,两个0-1之间的数相加是有概率大于1和小于1的。大于1的数向下取整得到1,小于1的数向下取整得到0,也就是说random_tensor是由0和1组成的,这点和dropout的实现也比较类似。
最后我们对输入x的每个值都进行缩放,即除以keep_prob(与dropout的缩放方式一致),乘以random_tensor得到输出output。举个例子,比如说输入x的batchsize为2,可以理解成这组输入由两组样本,样本1和样本2的值有概率全部被置0。
再举一个极端的例子,如果我们设置batchsize为1,也就是说每次我们只输入1个样本,这1个有概率全部被置0。如果我们在某个分支使用droppath,该分支的输出可能为0,从网络结构上来看这个分支就相当于被删除掉了。
代码讲解详细见视频
作用
使用dropout,droppath方法可以减少神经元提取的特征,分支之间的耦合度(也就是减少相互依赖的程度)。可以防止过拟合。但是前提是设置的超参数一定要合理。
2.layer normalization
总觉得论文源码,或者说pytorch官方实现的LN有问题?
因为根据何凯明的论文《Group Normalization》来看
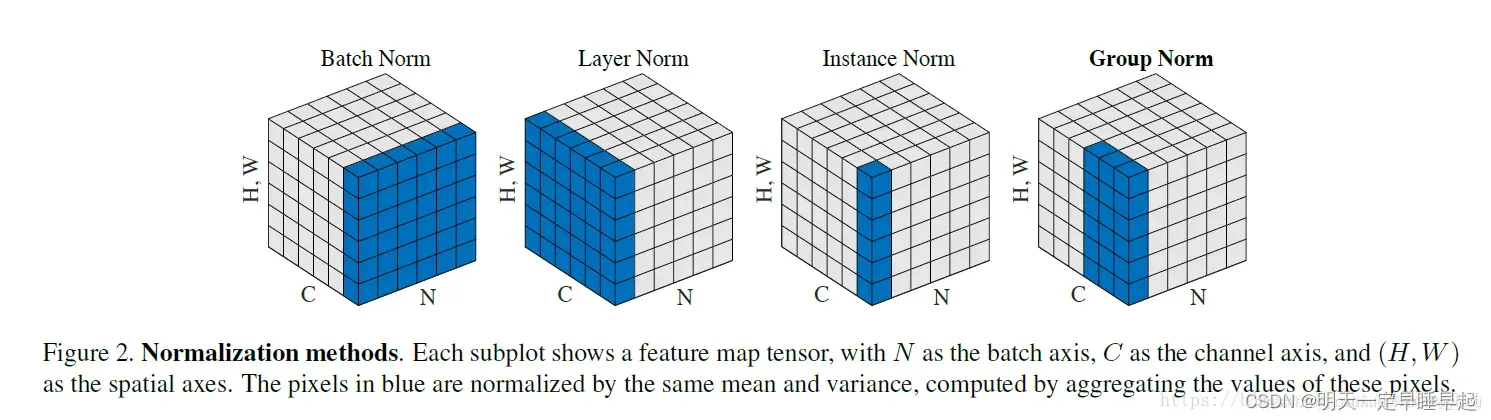
即每个像蓝色这样的区域会计算出一个均值和方差,在这个蓝色区域内的元素都会用这个均值和方差进行归一化。
LN相当于计算bachsize中每个batch的均值和标准差,按理来说应该最后计算出batchsize个均值和方差。但是根据官方实现的源码(以channel first为例,假设输入的shape是)
u = x.mean(1, keepdim=True)
s = (x - u).pow(2).mean(1, keepdim=True)
x = (x - u) / torch.sqrt(s + self.eps)
可以看到均值计算是按照索引1也就channel维度来计算的。但是这样子导致的结果就是会计算出个均值和标准差,和上面论文的图对应不上。如果按照源码计算的方式,那么图片应该改成这个样子:
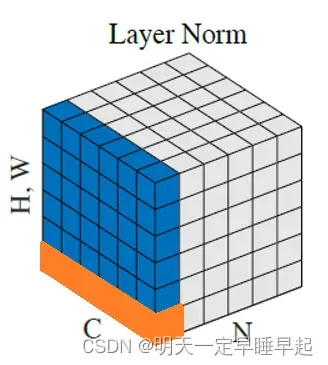
注意图片里面橙色的部分,这部分才是pytorch实现的LN计算的均值和标准差所使用的元素。即每个像橙色这样的区域会计算出一个均值和方差,在这个橙色区域内的元素都会用这个均值和方差进行归一化。
还有一点需要注意的是,官方实现的LN当中有一个参数elementwise_affine
如果elementwise_affine设置为True,则对归一化后的batch进行仿射变换,即乘以模块内部的weight(初值是[1., ]*dim)然后加上模块内部的bias(初值是[0., ]*dim),这两个变量会在反向传播时得到更新。
如果elementwise_affine设置为False,则LayerNorm中不含有weight和bias两个变量,只做归一化,不会进行仿射变换。
3.Depthwise Convolution
目标检测 — Depthwise Convolution(深度可分离卷积)原理与思考这篇文章已经讲的非常通俗易懂了。但是这里要吐槽一下,Depthwise Convolution和深度可分离卷积应该不是一回事。准确来说深度可分离卷积是Depthwise separable convolution,而Depthwise separable convolution是由Depthwise Convolution和Pointwise Convolution组成。具体可以参考深度可分离卷积(Depthwise separable convolution)
实际调用的时候也发现了Depthwise Convolution的一些细节:
DW卷积主要通过修改nn.Conv2d()中的group参数,group参数默认是1,即输入默认分为1组,表示普通卷积。假设我们输入卷积的特征图通道数为,经过卷积后输出的通道为
。此时相当于所有通道的特征图分别经过
个不同的卷积核计算得到输出特征图的其中一个通道,因此我们共需要
个不同的卷积核。如图所示:
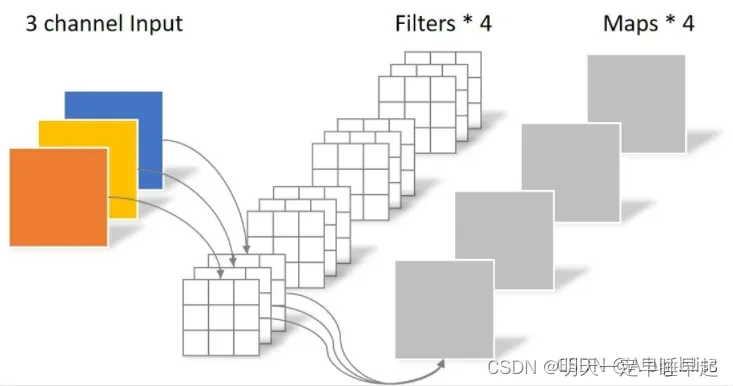
举个例子,我们不考虑偏置,定义如下卷积层并观察权重weight的shape
conv = nn.Conv2d(3, 6, kernel_size=1, padding=0)
conv.weight.shape
输出:
torch.Size([6, 3, 1, 1])
表示的含义是该卷积层共有个
的卷积核。
当group不为1时,我们直接上代码举个例子。
# 定义输入的值和shape
x=torch.range(1,3*2*2).reshape(1,3,2,2)
# 定义DW卷积
dwconv = nn.Conv2d(3, 6, kernel_size=1, padding=0, groups=3)
# 设置DW卷积的权重便于分析
dwconv.weight.data=torch.range(1,6).reshape(6,1,1,1)
# 令偏置为0
dwconv.bias.data=torch.tensor([0.0]*6)
output=dwconv(x)
输出:
x=tensor([[[[ 1., 2.],
[ 3., 4.]],
[[ 5., 6.],
[ 7., 8.]],
[[ 9., 10.],
[11., 12.]]]])
dwconv.weight.data=tensor([[[[1.]]],
[[[2.]]],
[[[3.]]],
[[[4.]]],
[[[5.]]],
[[[6.]]]])
output=tensor([[[[ 1., 2.],
[ 3., 4.]],
[[ 2., 4.],
[ 6., 8.]],
[[15., 18.],
[21., 24.]],
[[20., 24.],
[28., 32.]],
[[45., 50.],
[55., 60.]],
[[54., 60.],
[66., 72.]]]], grad_fn=<MkldnnConvolutionBackward>)
假设我们的输入x的shape为,我们可以理解成1张2*2的3通道图片,手绘一个图以便理解计算过程
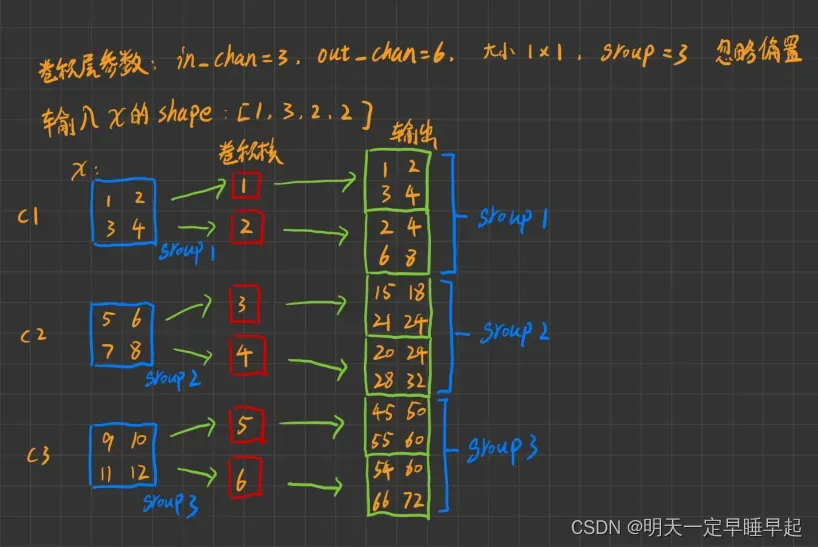
我们再来思考一个问题,我们要怎么知道DW卷积使用了多少个卷积核呢?我们不妨换个角度来看待DW卷积。已知in_chan=3,out_chan=6,group=3,我们可以把输入和输出的chan都分为group组。这样,我们输入的group1、group2、group3均由1个通道表示,输出的group1,group2,group3均由2个通道表示。我们仅观察输入和输出的1个group,比如输入和输出的group1。此时我们再把输出看成是输入执行普通卷积的结果,也就是说,相当于输入通道数1,经过普通卷积之后通道数变成2,因此需要个卷积核。如图所示

这只是group1的情况,我们共有3个group,因此DW卷积的卷积核个数为。
更一般的情况下,DW卷积使用的卷积核数量公式如下
而普通卷积需要的卷积核个数为
作用不言而喻,减少了参数量,使得网络可以加深。不过也有一些帖子讨论到代价是提升了IO的读取次数(大约100倍)。而且要注意一点,out_chan和in_chan必须整除group,否则会报错。
好像mobilenet、Xception和efficientnet都有使用到。
另外根据ConvNeXt网络详解中提到的,论文作者认为depthwise convolution和self-attention中的加权求和操作很相似。这一部分不理解。
4.结构层面
先引用ConvNeXt网络详解里面讲的一段话:
为什么现在基于Transformer架构的模型效果比卷积神经网络要好呢?论文中的作者认为可能是随着技术的不断发展,各种新的架构以及优化策略促使Transformer模型的效果更好,那么使用相同的策略去训练卷积神经网络也能达到相同的效果吗?抱着这个疑问作者就以Swin Transformer作为参考进行一系列实验。
接下来再做一些补充。
4.1.MLP to Inverted Bottleneck
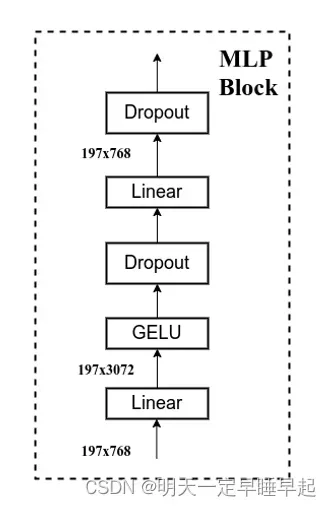
回顾MLP Block,我们重建关注特征图通道数的变化:,我们可以把它理解成两头细中间粗。作者认为Transformer block中的MLP模块非常像MobileNetV2中的Inverted Bottleneck模块,如图所示:
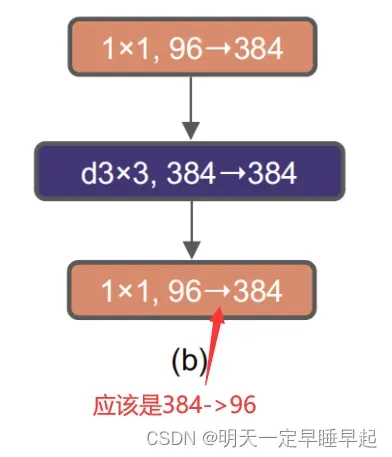
图中紫色的33卷积应该就是DW卷积,剩下11卷积就是普通卷积。注意到Inverted Bottleneck也同样是96->384->384->96两头细中间粗。
但是convnext最终采用的是
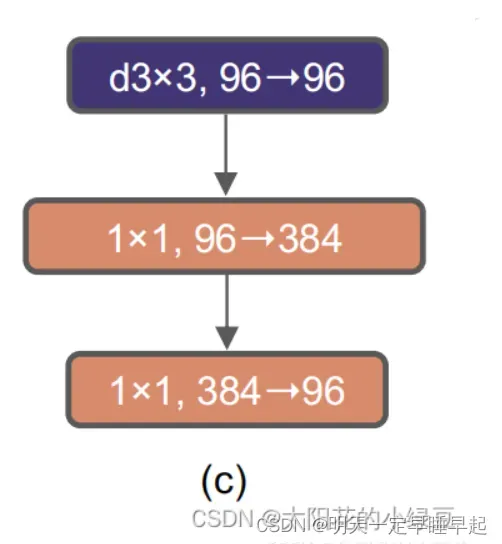
交换了33卷积和11卷积的位置是因为在Transformer中,MSA模块(multihead self-attention)是放在MLP模块之前的,所以这里进行效仿,将depthwise conv上移。也就是说用33的DW卷积效仿MSA,后面两个11卷积效仿MLP。
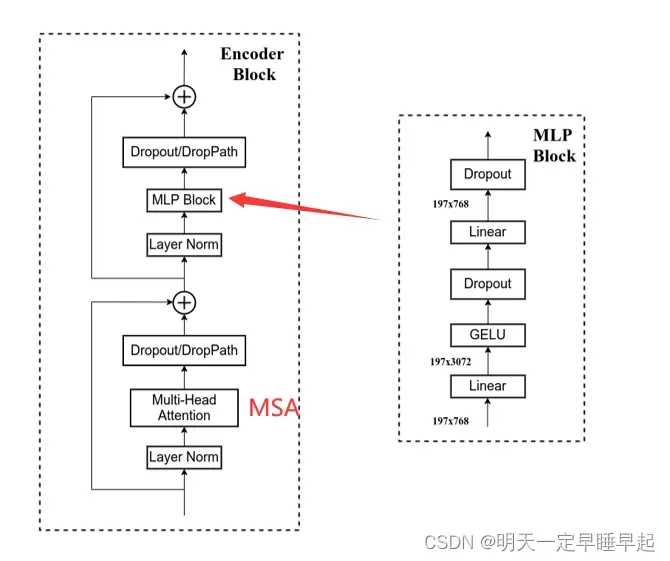
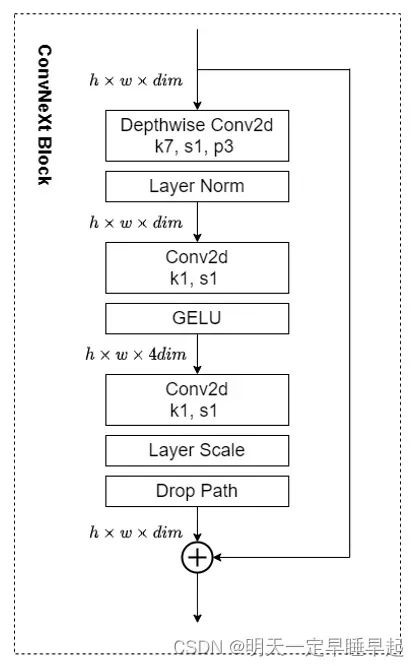
对比下还是有些异曲同工之妙的,区别是convnext block相比VIT encoder还少了一部分残差。具体也可以看下面对比图
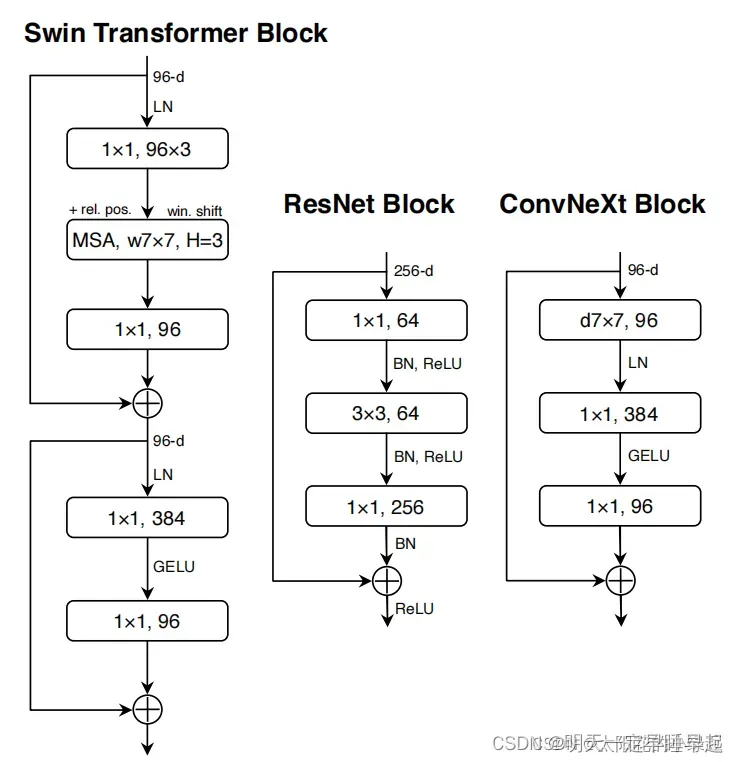
4.2.整体对比
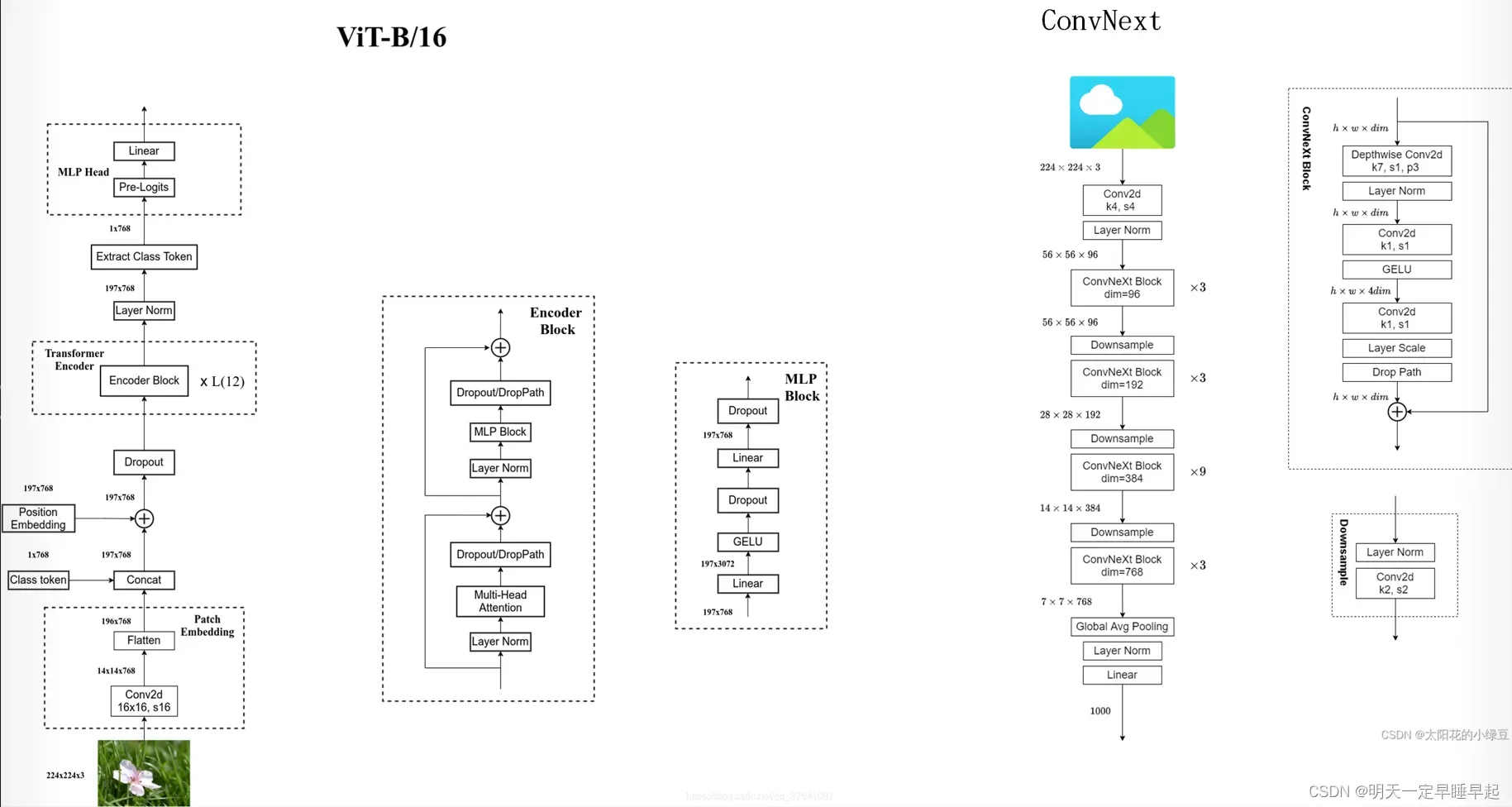
左边是VIT,右边是ConvNext。convnext的第一个(k4,s4)卷积层可以看做VIT的patch embed。convnext block可以看作是encoder block。堆叠的convnext block可以看作是VIT堆叠的encoder block(其实应该以swin transformer做参考)。
5.代码
代码写的太优雅了,各种技巧妙用。代价就是为了增强拓展性牺牲了一些可读性。
比如avgpool是手动实现的,不明白为什么不直接调用API。不过写的也很巧妙
return self.norm(x.mean([-2, -1])) # global average pooling, (N, C, H, W) -> (N, C)
N表示batchsize,C表示通道数,H,W表示图像宽高。
画个图理解下:
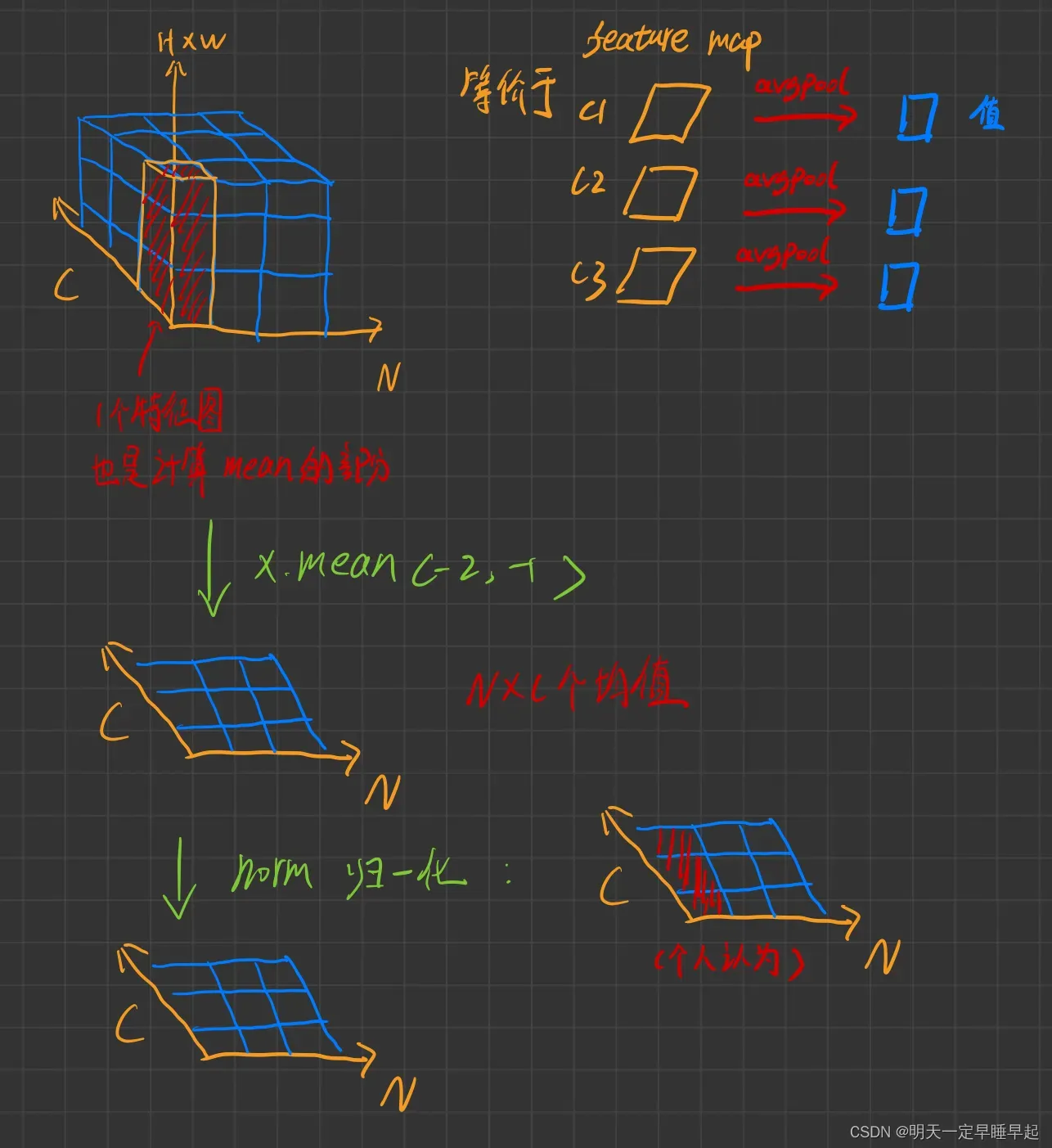
注意最后的norm归一化对应代码里面的self.norm,其实是一个LN层。个人认为它的计算方式应该是图中的那样(红字个人认为那里)。以红色区域的元素计算均值和标准差,然后红色区域的每个元素在根据这个均值和标准差进行归一化。
参考:
- 深度学习:Dropout如何解决过拟合
- Dropout
- 神经网络Dropout层中为什么dropout后还需要进行rescale?
- 10.1 EfficientNetV2网络详解
- 【正则化】DropPath/drop_path用法
- 15、Dropout原理以及其TF/Torch/Numpy源码实现
- 深入理解NLP中LayerNorm的原理以及LN的代码详解
- 目标检测 — Depthwise Convolution(深度可分离卷积)原理与思考
- Depth-wise Convolution
- 深度可分离卷积(Depthwise separable convolution)
- ConvNeXt网络详解
- pytorch LayerNorm参数详解,计算过程
文章出处登录后可见!
