第八章——降维
一、降维
降维定义
降维dimensionality reduction:通过某种数学变换将原始高维属性空间转变为一个低维空间。

降维可以增加计算效率,提高计算精度。在数据压缩,噪音消除、图像识别等领域有着广泛的应用。
事实上,很多高维数据都处在一个低维超平面上,其本质维数都非常低!!!
单个人脸的近似本质维度等于4
降维与特征选择
🍎 特征选择:直接选择特征子集用于模型训练,保留的特征没有发生任何改变
三种技术:过滤式(与学习任务无关),包裹式(特征选择依赖于学习器),嵌入式(特征选择与模型学习融为一体,模型中暗含子集选择)
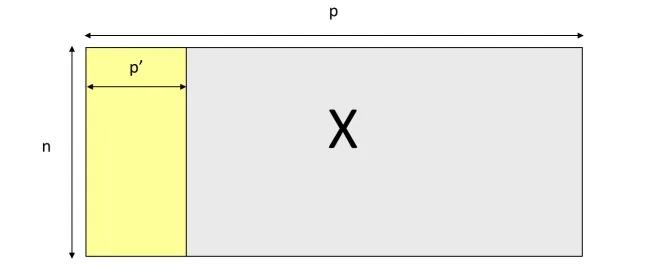
🍑 降维:通过某种数学变换将原始高维属性空间转变为一个低维空间,在低维的空间表示一般是稠密的。
降维没有抛弃掉任何原始特征,不是原始特征集的子集
降维方法分类
线性降维方法
PCA(Principal Component Analysis):主成分分析
FA(Factor Analysis) 因子分析
CCA(Canonical correlation analysis)典型相关性分析
非线性降维方法
Kernel PCA
LLE(Locally Linear Embedding)
Isomap (Isometric mapping)
t-SNE:画图降维
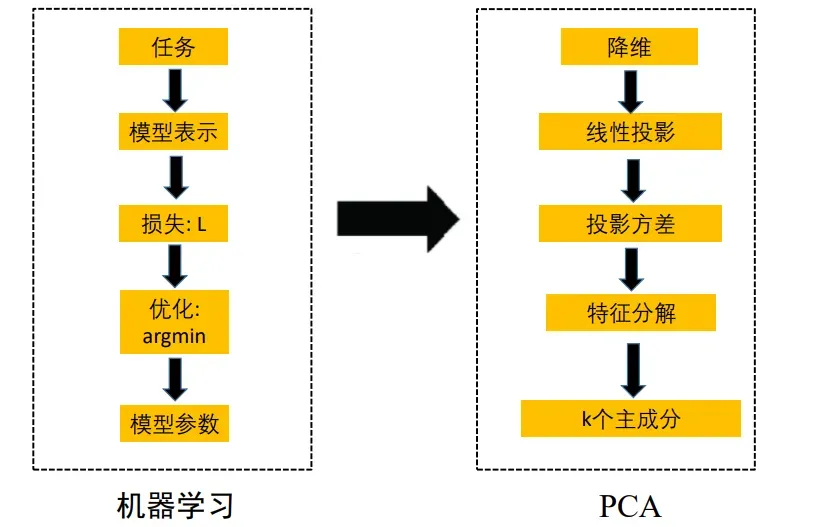
二、PCA
、
引入
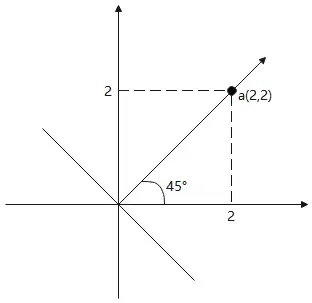
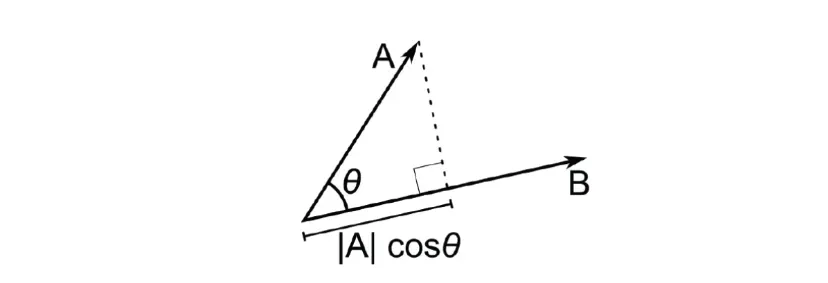
点乘:
假设|B|=1,则
投影向量即:
将数据点投影到新的低维空间
KaTeX parse error: Undefined control sequence: \ at position 137: …是一个p\times m的矩阵\̲ ̲
1️⃣ 数据居中处理:
中心化以后:
2️⃣ 选择一组长度为1的正交基 (𝒘𝟏, ⋯ , 𝒘𝒌)——k<p 时,就是降维处理
3️⃣ 点在新坐标系下(新的基向量)的坐标通过点乘表示
4️⃣ 在新基下的数据表示(重构)
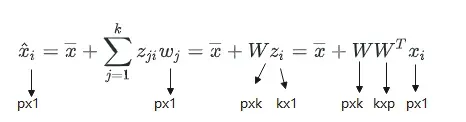
举例说明:
PCA——主成分分析技术
PCA基本思想:构造原始特征的一系列线性组合形成的线性无关低维特征,以去除数据的相关性,并使降维后的数据最大程度地保持原始高维数据的方差信息。
右图比较好
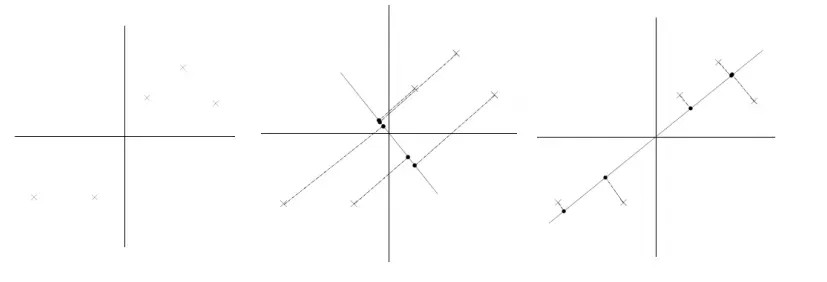
最大投影方差
思想:给定高维空间数据,找到低维子空间使得数据在此 空间投影后,信息(方差)能尽可能大的保持
表现度量:最大投影方差
最小投影距离
思想:给定高维空间数据,找到低维子空间使得数据在此空间投影后,投影数据与原数据之间的最小平方距离尽可 能小(尽可能重建原数据)
表现度量:最小投影距离
最大投影方差
第一主方向:最大方差投影方向
第一主成分:数据在第一主方向上的投影
方差
目标函数即:
利用了
最后有:
可以构造朗格朗日函数:
所以w是A的特征向量,当w为协方差矩阵的最大特征值对应的特征向量时,方差α取到最大值
已经求出第一个主方向,之后的主方向:依次与前面的主方向正交,且方差尽可能地大
第二主成分的目标函数如下:
可以推导出:第k个主成分的目标函数的最大值为第k大特征值对应的特征向量
所以综合k个主成分,可以得到最终的目标函数:
矩阵的迹,数学、线性代数名词,在线性代数中,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)。
PCA主方向 = 数据协方差矩阵的特征向量
更大特征值对应的特征向量更加重要
降维的结果为:
重构的结果为:
PCA算法步骤
目标:计算数组k个主方向
1️⃣ 数据居中
2️⃣ 计算居中数据的协方差矩阵
3️⃣ 计算协方差矩阵最大k个特征值对应的特征向量,组成矩阵
输出降维结果:
降维后,信息有所损失。但是如果特征值非常小,损 失的信息很少
举例说明
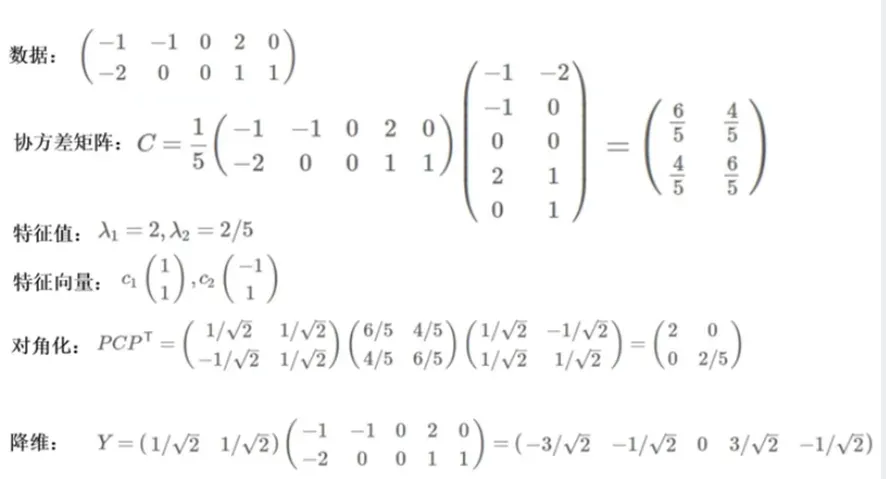
归一化后得到W即
重构后:
最小投影距离
目标函数:最小化与
之间的距离
最小原数据与投影数据间距离与最大投影方差等价
三、PCA应用:人脸识别
人脸识别:对所有人脸计算其子空间,然后在其计算 子空间坐标投影,利用低维坐标进行识别
训练数据X:图片尺寸*图片个数

人脸重构:使用特征脸(主成分)重构的效果
每一个人脸都是特征脸(主成分)的线性组合
算法步骤
给定一张新的图片x:
将其投影到前k个主成分张成的低维空间中
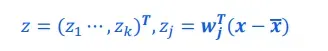
计算重构图片和重构误差

如果重构误差大于某个阈值,认为图片不是人脸图片
若重构误差小于阈值,认为该图片是人脸图片。在k-维空 间中,利用最近邻对新图片进行分类
SVD分解
非常大,通常大于10000
通过使用SVD进行加速
加速原理:通过计算
的特征值和特征向量,得到
的特征向量,即特征脸。
奇异值分解:
对于任意一个p×m的矩阵A,不妨假设p>m(维度大于个数), 它可以被分解为

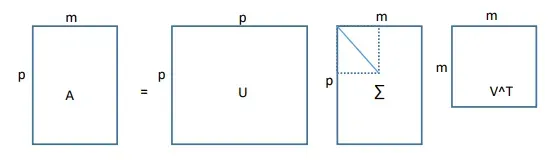
奇异值分解得到的矩阵U,Σ,V 满足如下性质:
U是
所有特征向量组成的矩阵
∑中对角线元素的值是矩阵
特征的平方根
V是
所有特征向量组成的矩阵

文章出处登录后可见!
