指纹是一种非常有用的低分辨率的分子表征,其形式多种多样。在过去几十年中,指纹已被应用于解决各种问题。扩展连通性指纹(Extended Connectivity Fingerprints,ECFP)是当下最广受使用用于构建化合物定量构效关系(QSAR)模型的分子指纹。
ECFP 于 2000 年随着 Pipeline Pilot 的发布而首次引入。在 RDKit 中,ECFP 指纹又叫 Morgan 指纹,其原因为ECFP的核心思想来自于 Morgan 算法,该算法试图为分子中的每个原子分配一个唯一的、连续的编号。独特的原子编号是所有广泛使用的分子识别方法(包括InChI、SMILES、CAS registry等)的基础。
需要注意的是:以下“编号”实际对应的英文名为Identifier,也就是标识符,是指用来标识某个实体的一个符号,在不同的应用环境下有不同的含义。“编号”不仅仅是1、2、3、4、5,这里为了好理解,均翻译为编号。
1. Morgan算法的原理
Morgan 算法名字来源于1965年 Morgan 发表的论文,该算法分两步进行:
**第一步:**枚举所有可能的原子编号,遵循规则为:
(1)开始位置随机:
如下面图片所示,选择一个随机原子并标记为“1”。
(2)遵照一定的顺序,相邻原子编号相连:
原子1的每个未标记的相邻原子都按随机顺序迭代,并分配给该原子下一个最高的可用数字(“2”、“3”,以此类推)。例如,如果选择了A为1,B就是2。如果选择B为1,A、C、D均可以为2,如果A为2,C和D其中一个为3;如果C为3,则D为4;如果D为3,则C为4。
(3)每个原子只分配一个唯一的编号:
每个新标记的原子按照其编号进行迭代,并按照步骤2对其相邻原子进行编号。这个过程一直持续到所有原子都被编号为止,其结果是分子中的每个原子都有一个唯一的编号。
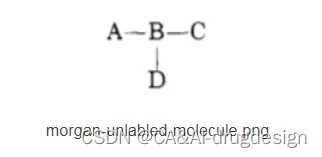
图1 例子
如上图所示,可能出现12种分配方案

图2 分配方案
**第二步:**将上述所有的分配方案进行一一去除,直到只剩下一种分配方案。
在去除时,需要计算每个原子的连通性(Connectivity value),这也是扩展连通性指纹命名的由来。连通性,简单来说就是原子的连接情况。如何计算原子的连通性呢?首先,分子中的每个原子被分配一个初始的 “连接值”,该值等于与之相连的原子的数量。然后,进行迭代,用一个新的”连接值”取代之前的”连接值”,这个新的”连接值”是由相邻的”连接值”之和计算出来的。如下面例子,values为这些”连接值”的多样性,即多少个唯一的值,当 values开始下降则停止迭代。如下图的例子,当 n为6时,发现 values不再变化,则使用n=6的情况。
最后一轮的”连接值”被用来消除分配方案,最终使得分子中原子都具有唯一的原子编号。如下图,按照蓝色箭头右边的顺序分配原子的序号,比如最右边的C为第1位,接着是与之相连的C(3),在这个分叉口,如果按照随机原则,我们可以选择双键的O,也可以选择单键的O。但是,有了这个优先级,我们可以确定直接用双键O(1),因为双键O(1)的顺序要由于单键O(9)。
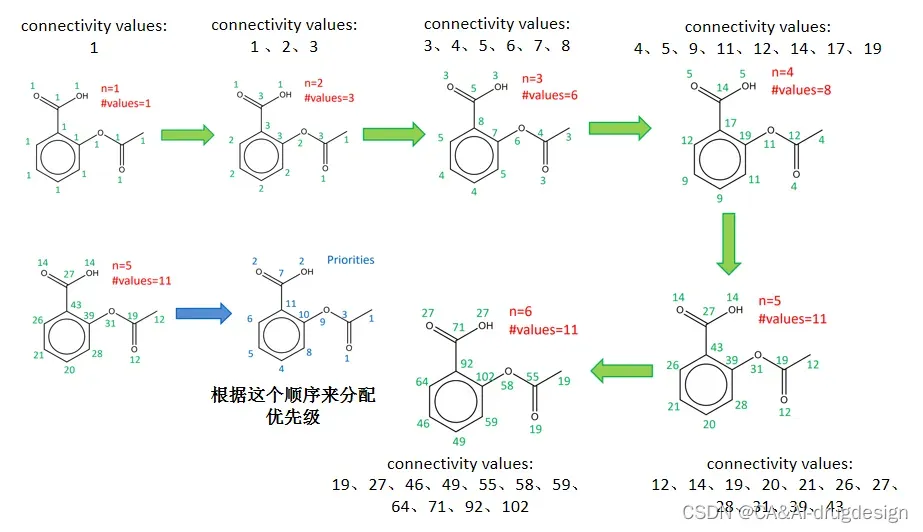
图3 如何去除分配方案
Morgan算法也有些不足的地方:
(1)不变量非常简单
(2)最初无法区分不同原子类型的键序
(3)数值爆炸
(4)并不是所有的原子都能被很好地区分……
Weininger et al.等人提出了CANGEN 算法来克服这些不足:
(1)改进的不变量
(2)“稳定”优先级
(3)避免组合不变量引起的歧义
(4)解决“对称”原子
类似的程序用于通过 CANGEN 算法生成唯一的 SMILES。然而,在这种情况下,分配给每个原子的初始值要考虑到以下的原子不变量:
(1)原子连接数。
(2)非氢键的数量。
(3)原子数。
(4)电荷的符号。
(5)绝对电荷。
(6)连接氢的数量。
这些属性可以方便地被编码为整数值。尽管CANGEN论文中使用的术语是 “不变”,在本文中这些值将被称为 “原子标识符”(个人定义,原子编号)。我们以下结构为例介绍如何通过 CANGEN 算法生成唯一的 SMILES。
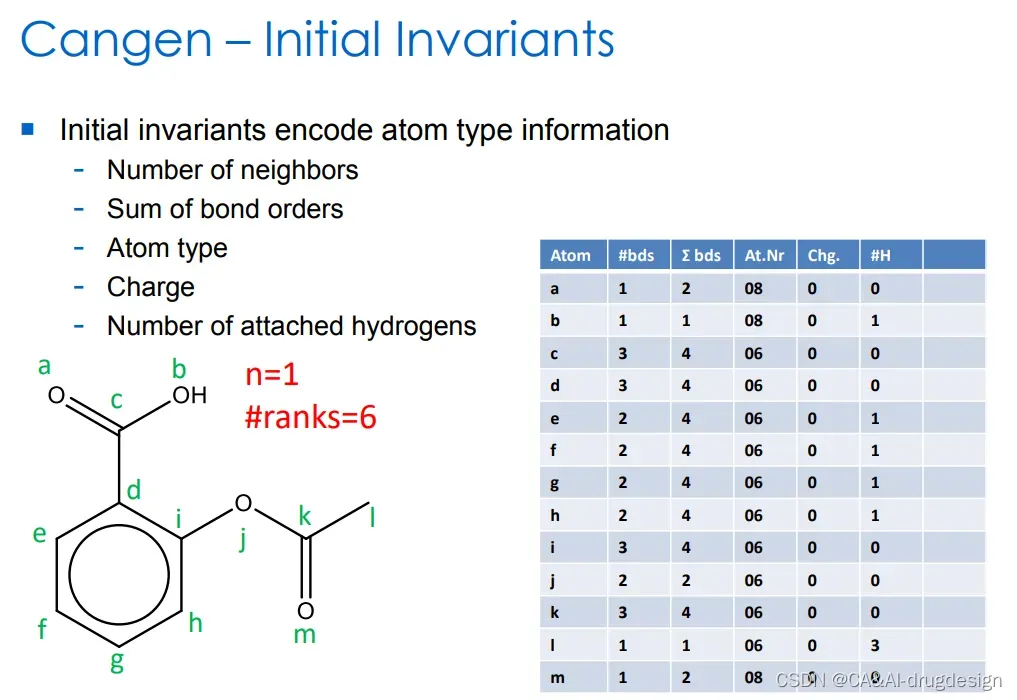
图4 起始不变量
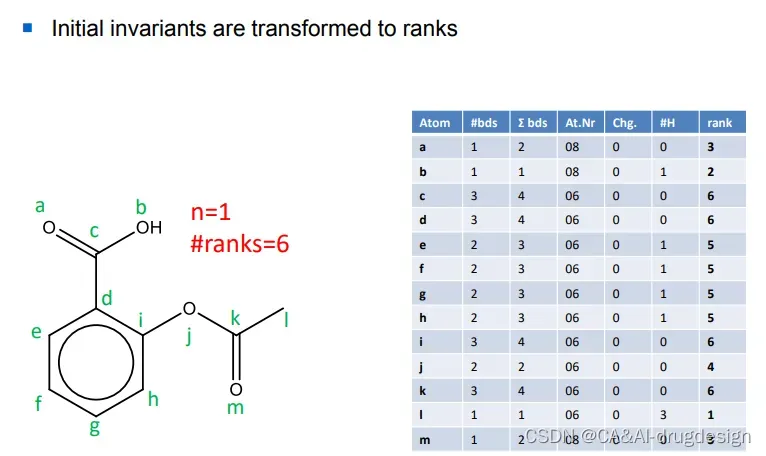
图5 起始不变量转变为排序(rank)
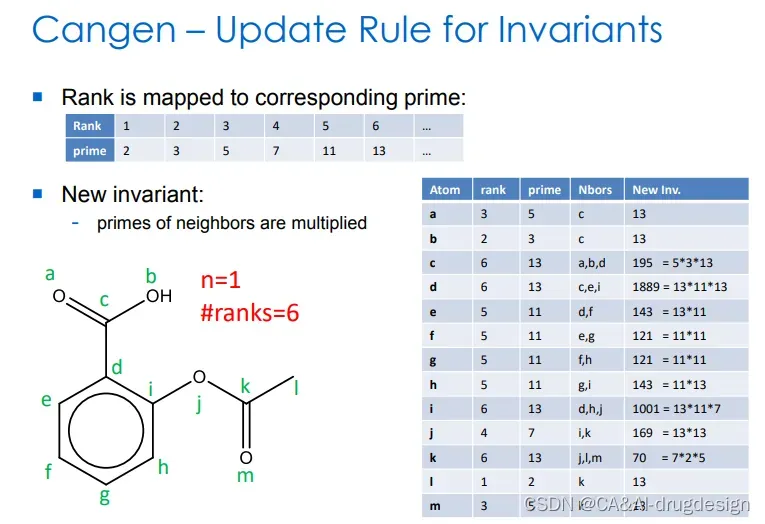
图6 对不变量更新规则

图7 得到新的排序(new rank)
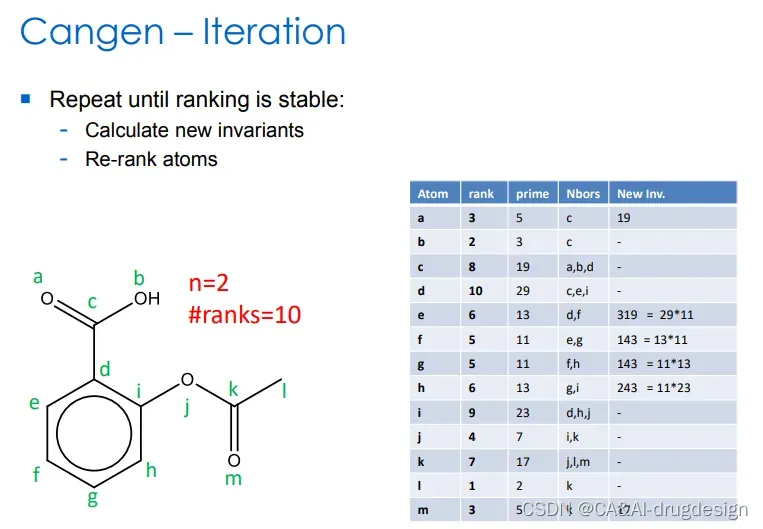
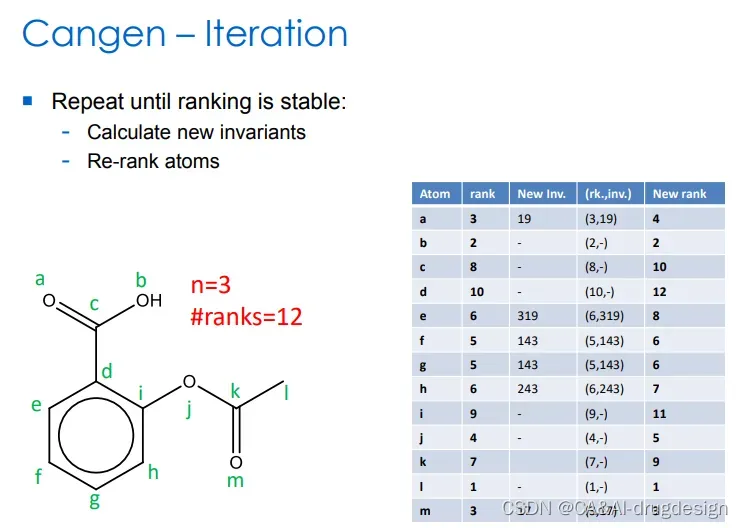
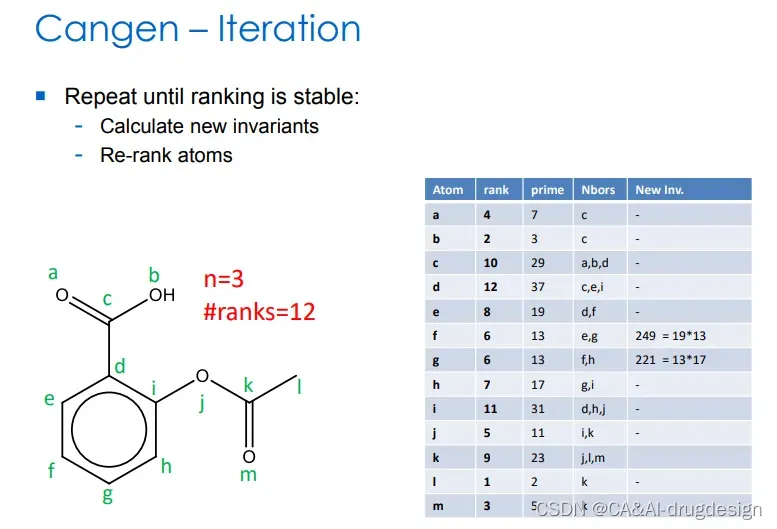
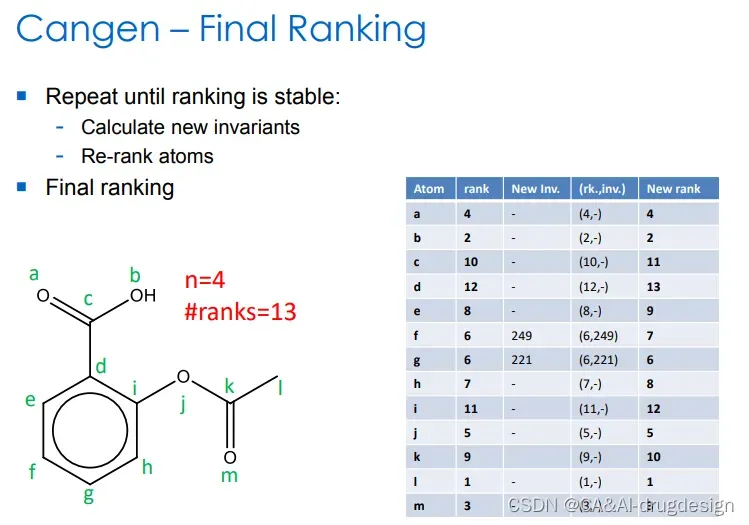
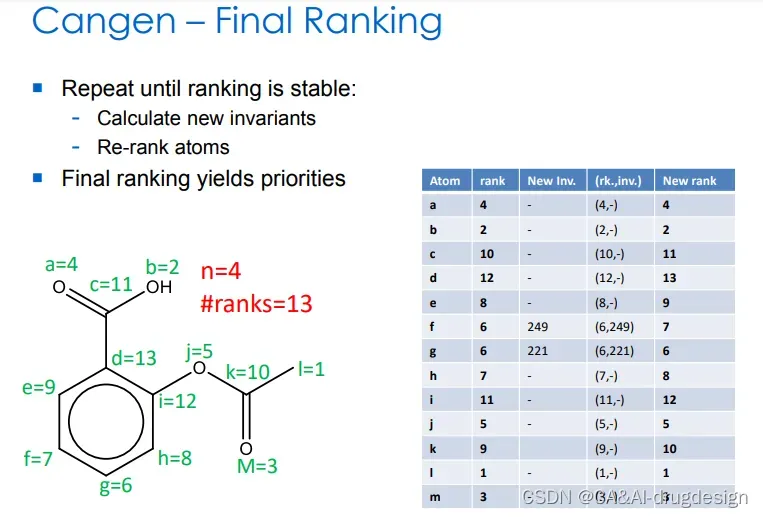
图8 重复,直到新的排序稳定
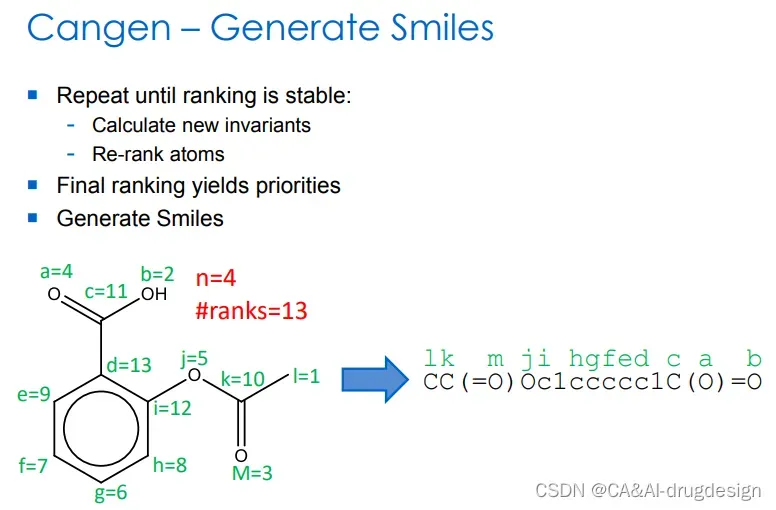
图9 生成smiles
2. ECFP的原理
ECFP是一种环形指纹(Circular fingerprint),术语 “扩展连接 “(Extended Connectivity)和 “环状 “(Circular)暗示了ECFP和Morgan算法之间的潜在联系。在ECFP中,分子中的每个原子都可以被看作是一个环形的中心。我们可以通过首先检查某原子相邻的原子,然后是这些相邻原子的相邻原子,依此类推,迭代地收集该原子的信息。然而,生成ECFP的算法在两个重要方面与Morgan的算法不同:
- 存储中间原子的原子编号。
- 不需要一组完全唯一的原子编号,这使得我们可以进行进一步优化。
一个 ECFP 被定义为每个感知半径的所有原子编号的集合,直到极限 n。 随着感知半径的扩大(n 增加),这个集合包括在以前和当前迭代中发现的所有原子编号。例如,n=0时,ECFP由一组唯一的原子编号组成,也就是说只考虑原子本身。n=1 时,我们检查每个原子及其直接相邻原子,来计算原子编号,从而扩充 n=0 的集合,以组成n=1的 ECFP。n增大时,依此类推。n=1 时称之 ECFP_2,n=2 时为 ECFP_4,以此类推。
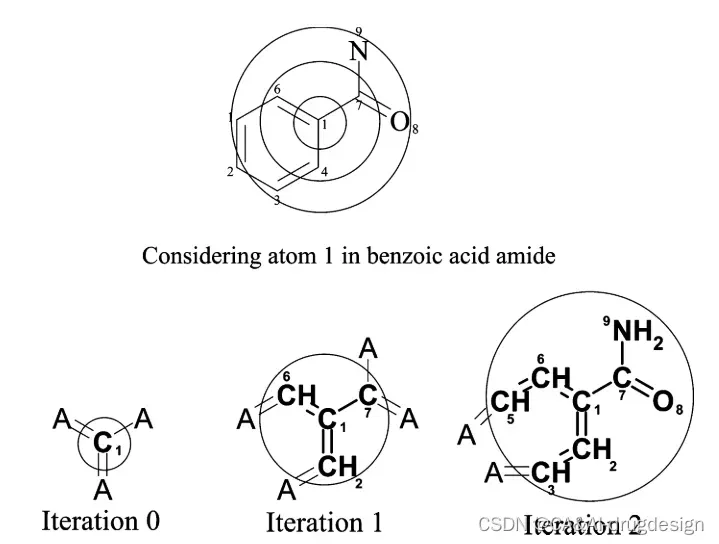
图10 感知半径的意义
迭代更新对原子编号表示的信息的影响的说明。 在这里,我们考虑苯甲酸酰胺中的原子 1。 如图顶部所示,每次迭代的效果是创建一个原子编号,该编号代表中心原子周围越来越大的圆形子结构。 在第 0 次迭代(即初始原子编号)时,原子仅表示有关原子 1 及其连接的键的信息,并且可以由左下角的子结构表示(“A”表示除氢以外的任何类型的原子)。经过一次迭代,原子编号现在包含有关原子 1 的直接相邻原子的信息(如图底部中心子结构所示)。 经过两次迭代,所代表的子结构进一步增长,现在完全结合了酰胺基团以及大部分芳环,如右下角所示。
因此,ECFP原子编号可以被看作是一种特殊的子结构钥匙。这里,”子结构 “指的是一个中心原子和它的相邻原子(该相邻原子按照与中心原子的距离分组)。一个密钥的存在表明,相应的分子包含产生该密钥的子结构。
可以使用任何方便的方法来存储原子编号。 例如,某些应用程序可能使用类似集合的数据结构,例如 ES6 和 Python 中的 Set 类或 Java 的 java.util.Set 实现提供的数据结构。另外,也可以使用概率性的二进制数据结构,如布鲁姆过滤器等。
3. 计算ECFP
ECFP 计算分三个阶段进行:
(1)初始化。即给每个原子都分配一个整数编号。
(2)迭代更新。将该原子的相邻原子信息增加到该原子上。
(3)重复处理。同一特征的多个实例要么被删除,要么被计数。
仅仅从这个描述中就可以开发出简单的ECFP算法。例如,我们可以将ECFP建立在原子质量上。在步骤1中,我们将分子中每个原子的质量存储在一个集合中。这个集合成为Iteration 0(迭代0)的ECFP。
Iteration 1的ECFP可以通过继续该算法来准备。在已经获得的原子集上,我们再增加一组,该组由中心原子的原子质量和其近邻原子的质量之和组成。
根据具体的应用,重复的原子编号可能会被删除或计数。例如,如果一个应用只要求记录一个原子编号的存在,则可以删除重复项。另一方面,如果一个应用要求计算原子编号的出现次数,则可以使用计数器。
我们可以迭代地继续添加原子编号,直到任意感知半径 n。请注意,随着 n 的增加,每个原子编号携带的原子信息离中心原子越来越远。
ECFP的计算步骤
上一节中描述的简化算法省略了很多潜在的有用信息。在实践中,ECFP原子编号不仅仅是原子质量,还有其他更广泛的各种属性。下面是一种ECFP生成算法,可以处理任意的原子和键的属性:
(1)创建一个集合 (S),用于存储原子编号。
(2)使用32位的整数来标记每个原子,比如可以使用 Morgan 算法或者 CANGEN 算法(确保每个原子有一个唯一的编号),然后将他们哈希化。
(3)将每个原子编号添加到S中。
(4)如果n=0,算法结束。否则继续到步骤(5)。
(5)对于每个原子,创建一个“键列表”储存该原子周边原子的信息,该列表先根据键级(单键、双键、三建)排序,再根据周边原子编号大小排序。
(6)用如下信息填充上述列表:内容为 [n, identifier, bo1, aid1, bo2, aid2, …],其中 n 为迭代次数,开始为0,identifier为原子编号,bo1 为第 1 根键的键级,aid1 是第 1 根键所连原子的编号。
(7)计算第 6 步中的特征列表的哈希值,作为该原子新的编号。
(8)如果新算出的编号在结构上与 S 中的不重复,则加入到 S 中。
(9)如果 n>=2,则重复5的步骤,进入下一个迭代。
这里所谓结构上不重复,原论文给出了一个例子,从 O 出发和从 N 出发,当 n=2 时,都会出现图中圈出的子结构,由于他们“起始”原子不同,所以原子编号肯定也不同,但从结构的角度,他们是一样的,所以需要去除。
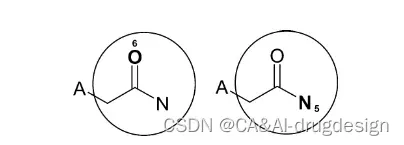
图11 重复结构
以氧(左)和氮(右)为中心进行两次迭代后的特征区域。由于这两个区域包含完全相同的原子和化学键,它们代表了重复的信息,尽管它们hash的原子编号值不同。
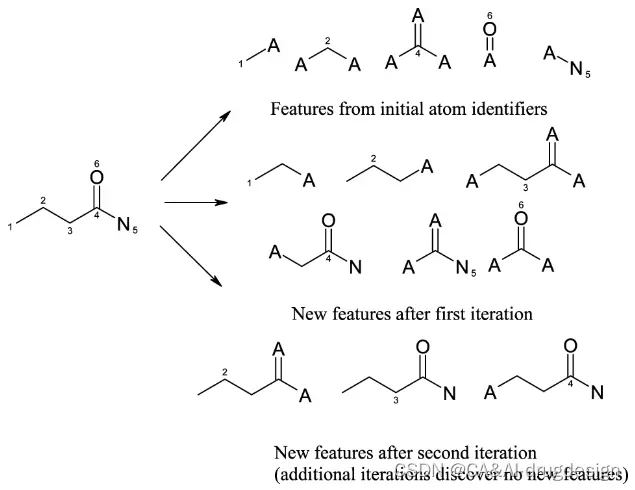
图12 丁酰胺的特征在去除重复后所代表的结构。该分子在初始赋值阶段产生五个特征(即唯一的原子标识符),在一次迭代后产生六个额外的特征,在两次迭代后产生三个特征。进一步的迭代没有产生新的特征。(图中的中心原子通过显示其原子编号来表示)。
4. Hash功能
Rogers和Hahn对要使用的哈希函数的问题有这样的说法。我们不描述在我们的计算中使用的特定哈希函数,因为任何 “合理的 “哈希函数都可以使用,而且结果的科学性是相同的。最重要的是让哈希函数将整数数组随机、均匀地映射到所有可能的整数的232大小的空间中;如果没有均匀的覆盖,碰撞率可能会增加,导致信息的损失。
换句话说,所需要的只是一个能够生成在足够大范围内均匀分布的标识符(编号)的哈希函数。
一个很好的候选者是循环冗余检查(CRC)函数之一,如广泛使用的CRC-32。这个哈希函数是由Alex Clark首次明确记录的,用于化学开发工具包的循环指纹实现。
CRC-32给定一个任意的字节数组,返回一个有符号的32位整数。大多数语言都有相应的实现。例如,CRC-32 Node JS包的工作原理如下。
一个很好的候选是循环冗余校验(CRC)函数之一,例如广泛使用的 CRC-32。这个散列函数首先由 Alex Clark 明确记录,用于化学开发工具包的环状指纹实施。
给定任意字节数组,CRC-32 返回一个有符号的 32 位整数。大多数语言都有实现。例如,CRC-32 Node JS 包的工作原理如下:
import hash from 'crc-32';
const feature = [ 1, 2, 3, 4 ];
const identifier = hash.buf(feature); // -1237517363
5. 联想
像任何指纹的实现一样,ECFP需要特别注意联想形式。特别是,必须为同一分子的所有联想形式生成相同的 ECFP。有两种概念上的方法是可行的:
(1)在计算 ECFP 指纹之前找到一个规范的联想形式。
(2)避免使用明确的键信息。
在这两种方法中,(2)似乎是最实用的。例如,对上面概述的针对键的算法做两点改变就可以消除联想形式简并。首先,确保原子不变量的计算包括原子的不饱和度。 其次,将步骤(6)替换为:
用如下信息填充上述列表:内容为 [n, identifier, aid1, aid2, …],其中 n 为迭代次数,开始为0,identifier为原子编号,aid1 是第 1 根键所连原子的编号。(我理解就是去掉了键的信息)
6. FCFP
如前一节所述,基本的 ECFP 算法可以进行修改。 “功能类指纹”(FCFPs,Functional-Class Fingerprints)与 ECFP 类似,都是通过迭代的方式将原子周围环境编译成一个分子指纹,与 ECFP 不同的是初始化时的原子特征。在 ECFP 中,原子的初始编号使用 CANGEN 算法中的方法,即由原子本身的几个性质得到,包括:
(1)原子连接数
(2)非氢化学键数
(3)原子序号
(4)原子电荷正负
(5)原子电荷绝对值
(6)连接氢原子个数
RDKit 中具体实现方法仅仅是用了(1)、(3)、(5)和(6)
FCFP使用了一个六位编码,其中设置一个位表示存在一个 “药效 “属性,这些”药效 “属性很像药物化学中的药效团,:
(1)氢键受体;
(2)氢键供体;
(3)负离子化;
(4)可正离子化;
(5)芳香原子;以及
(6)卤素
类似的方法可用于根据其他特征类的存在来分配原子编号,包括图形属性(例如,ring membership、氢的数量或立体化学构型)或物理属性(例如,pKa、电负性、同位素质量)。
RDKit 使用预先定义的 SMARTS来匹配该原子是否满足上述六种性质。可见 FCFP 所描述的原子本身信息更少,仅仅是描述原子所处的官能团环境,随着迭代的过程,FCFP 似乎在描述几个官能团之间的拓扑关系,比如 FCFP4 将反映距离为2根键内的药效团组合,如 O=C-Cl 这样。
7. 总结
ECFP主要有三个特点,这些特点最能反映出其优势:
(1)简单性。基本的ECFP算法是由很少的单元组成的,实现简单。
(2)灵活性。基本算法的许多变化都是可能的。
(3)易于计算。感知半径可以改变,以便在计算的复杂性和功能之间取得平衡。
参考文章:
- https://www.zealseeker.com/archives/ecfp-introduction/
- https://depth-first.com/articles/2019/01/11/extended-connectivity-fingerprints/#hash-function
3.https://bigchem.eu/sites/default/files/Martin_Vogt_algorithms_in_cheminformatics_150519.pdf - Rogers, David Hahn, Mathew. Extended-connectivity fingerprints. Journal of Chemical Information and Modeling. 2010.50(5).742-754.
文章出处登录后可见!
