目录

前言

一、回归定义

二、回归建模步骤

1.模型假设-线性模型（Linear Model）

（1）一元线性模型

（2）多元线性模型

2.模型评估-损失函数（Loss Funtion）

3.最佳模型-梯度下降（Gradient Descent）

三.常见问题

总结

前言

本文来源于李宏毅老师的机器学习课程。`

回归是一种有监督学习，主要是从中发现变量之间的相关性，确定变量间的关系式，从而预测输出的变量值。

一、回归定义

回归问题主要用于预测某连续变量的数值，例如：预测PM2.5、预测房屋价格、电商用户购买可能性等。

二、回归建模步骤

1.模型假设-线性模型（Linear Model）

（1）一元线性模型

对于输入变量只有一个，即单个的特征，线性回归表示如下：

代表y轴上的截距，代表特征的权重系数。

（2）多元线性模型

当输入变量不止一个时，即多个特征，线性回归表示如下：

在多元线性模型中，通过学习和

图片来源：李宏毅机器学习ppt 

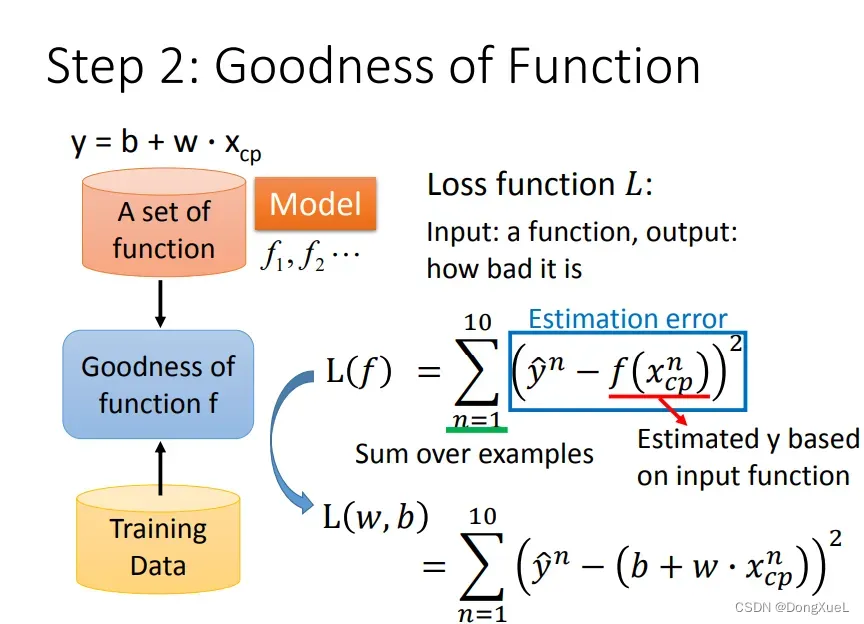
2.模型评估-损失函数（Loss Funtion）

Loss Funtion评价模型所产生的预测结果的一个函数，衡量一组参数的好坏，在线性回归则是中和的好坏，损失函数的反馈值是机器学习调整参数的重要依据。

• 输入：当前function
• 输出：当前function的好坏

对于回归问题，采用以下几种损失函数：

• 均方误差（MSE）

• 均方根误差（RMSE）

• 平均绝对值误差（MAE）

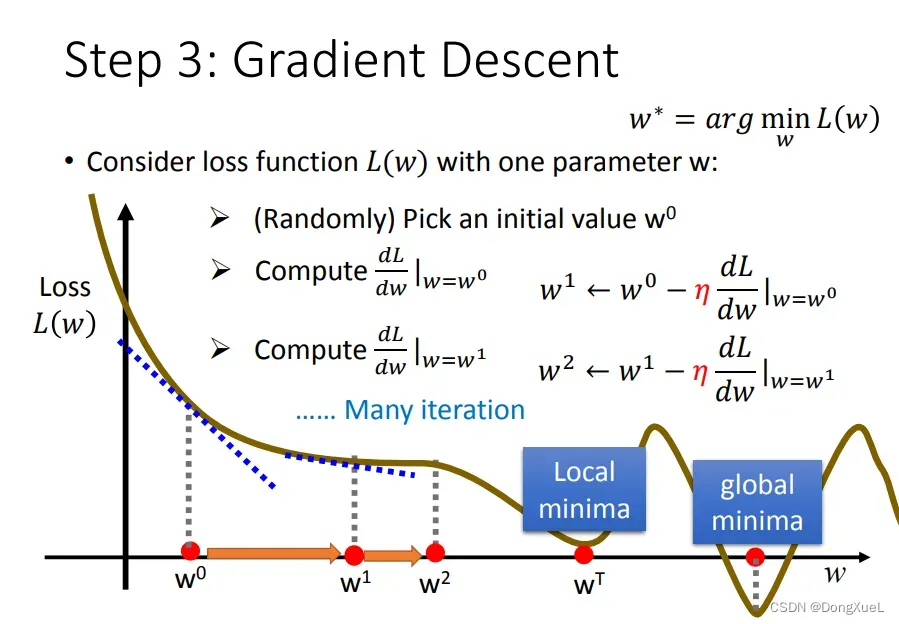
3.最佳模型-梯度下降（Gradient Descent）

选择损失函数值最小的作为最佳模型，公式表示为：

寻找习和常用方法：梯度下降法，其步骤如下：

• step1：随机选取一个点；
• step2：计算参数对损失函数的微分，即切线斜率。切线斜率为负，增加值；切线斜率为正，减少值；

代表学习速率(learning_rate)，即单次更新步长。如果太小更新速率太慢则很难到达；如果太大则容易直接越过极值点。

• step3：重复之前步骤，直到找到最低点

 常见梯度下降的方法：小批量梯度下降（MBGD）、Adam算法、动量加速梯度下降、Adagrad算法、RMSProp算法等。

 图片来源：李宏毅机器学习ppt

三.常见问题

欠拟合（underfitting）：学习器对训练样本未学习好，预测误差较大。（bias）

解决方法：增加特征数量、选用更复杂的模型。

过拟合（overfitting）：学习器把训练样本学习得过好，导致新样本进来后效果不佳，即训练集效果好，测试集不佳，模型泛化能力差。（方差）

解决方法：减少特征数量、增加训练数据、加入正则化、调整过于复杂模型。

总结

偏差、梯度下降在后续学习中再总结。