目录
前言
第一个典型的卷积神经网络(Convolutional Neural Network, 以下简称CNN)是由LeCun等人于1998年提出LeNet网络，是一种用于手写体字符识别的非常高效的卷积神经网络，是CNN的开山之作；但真正让CNN大放异彩的是AlexNet网络，在2012年在全球知名的图像识别竞赛 ILSVRC 中，AlexNet 横空出世，直接将错误率降低了近 10 个百分点，这是之前所有机器学习模型无法做到的，由此，开启了CNN席卷了各大视觉领域的狂热之旅，CNN也正式成为AI领域最重要的符号，成为从事AI人员竞相学习对象，随着CNN的蓬勃发展，众多网络模型也相继提出。
卷积神经网络的基本组成结构
近年来，随着人们对CNN的进一步研究，CNN模型结构日趋完善和统一，基本包括以下几个组成部分：卷积层、池化层、激活函数和损失函数，下面一一介绍。
一.卷积层
1.标准卷积层
卷积层是卷积神经网络的核心层，采用一组卷积核和输入图像进行卷积运算，完成图像的特征提取，图像经过卷积层计算后输出的结果称为输出特征图，特征图通道数与该卷积层使用的卷积核数量相同。
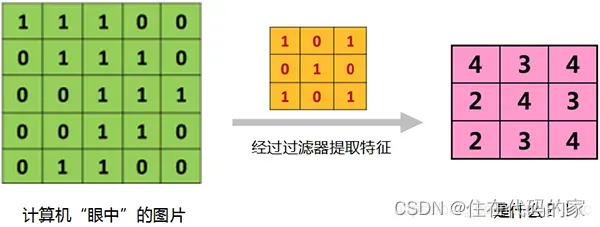
输入图像：上图的绿色矩阵，计算机中用图像的像素矩阵表达
卷积核：上图的黄色矩阵，是训练过程要训练的权重参数，矩阵中的数值可以随机初始化，矩阵的大小也可以自定义，如2×2，3×3，5×5等
输出特征层：上图的紫色部分，是输入图像与卷积层卷积之后的输出结果
以下图表示一个4×4大小的卷积核与一个5×5大小的输入特征图的卷积计算过程
第一步：
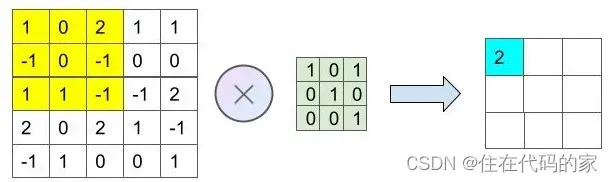
第二步：
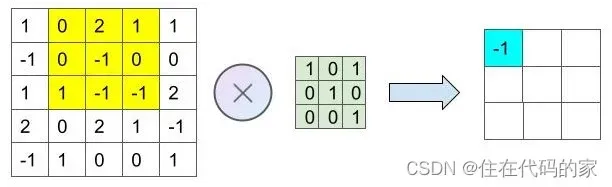
第三步：
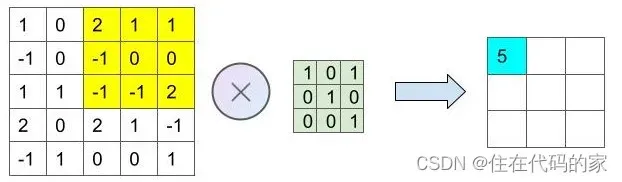
下面是标准卷积的动态计算过程
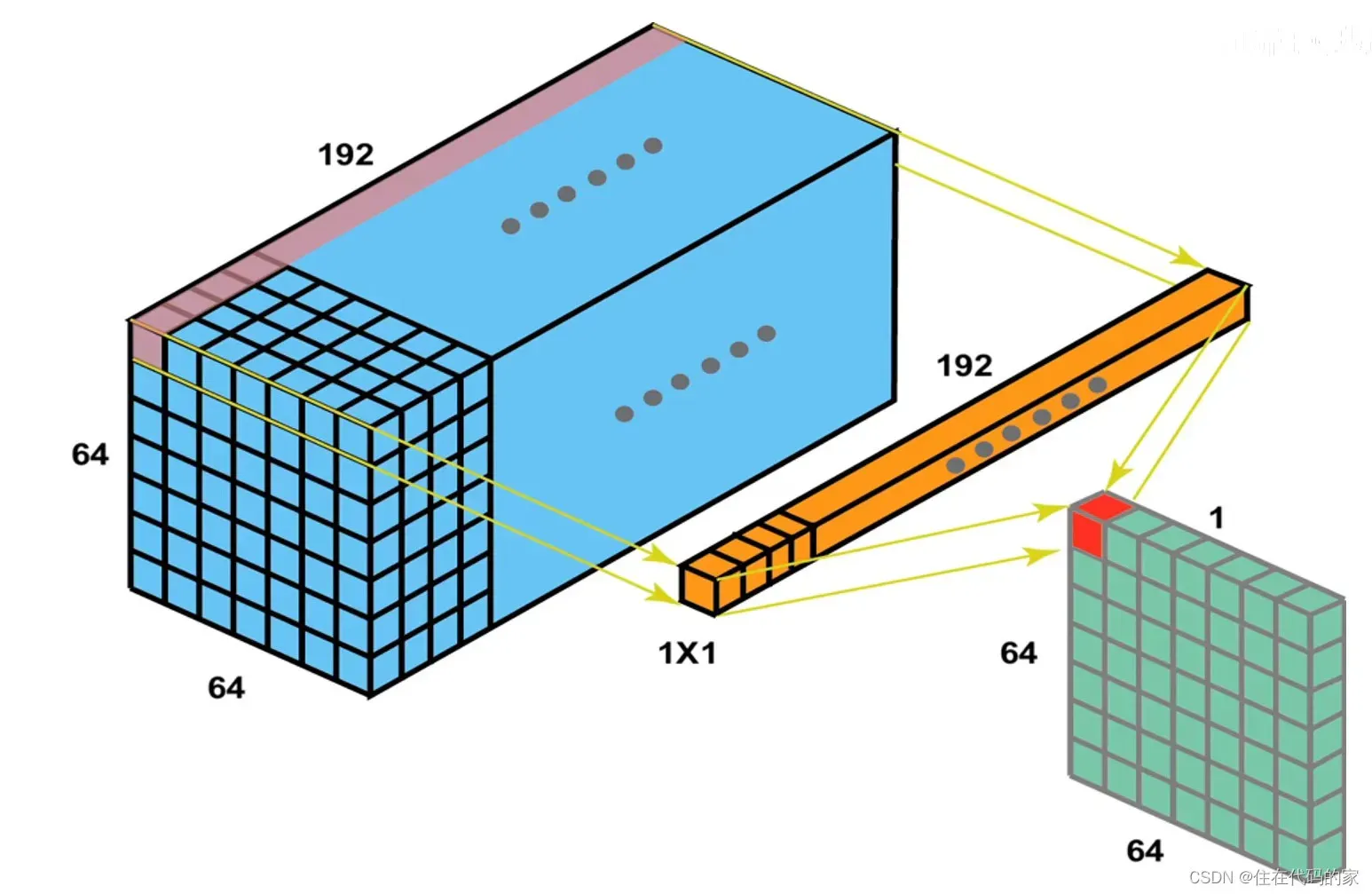
下面是标准卷积的立体特征图的计算过程（实际网络训练的真实过程）
2.形变卷积
定义：形变卷积的是相对于标准卷积的概念而来，在标准卷积操作中卷积核作用区域始终为中心点周围标准卷积核大小的矩形区域内，为了削弱这个限制，研究员们对卷积核中每个采样点的位置都增加了一个偏移的变量，通过这些变量，卷积核就可以在当前位置附近随意的采样，而不再局限于之前的规则格点，这样扩展后的卷积操作被称为可变形卷积。
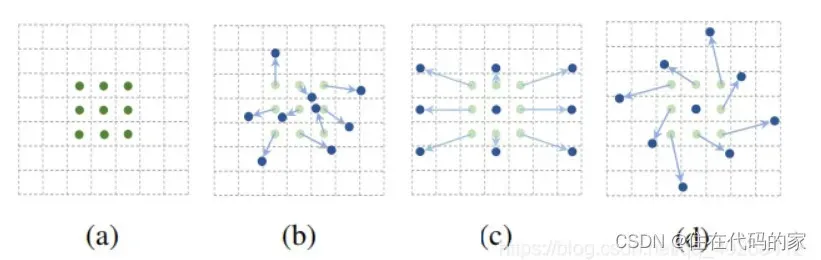
图(a) 为标准卷积，图(b)(c)(d)为形变卷积,可见在采样点附近增加了偏移变量
作用：可变形卷积核的大小和位置可以根据当前需要识别的图像内容进行动态调整，其直观效果就是不同位置的卷积核采样点位置会根据图像内容发生自适应的变化，从而适应不同物体的形状、大小等几何形变。
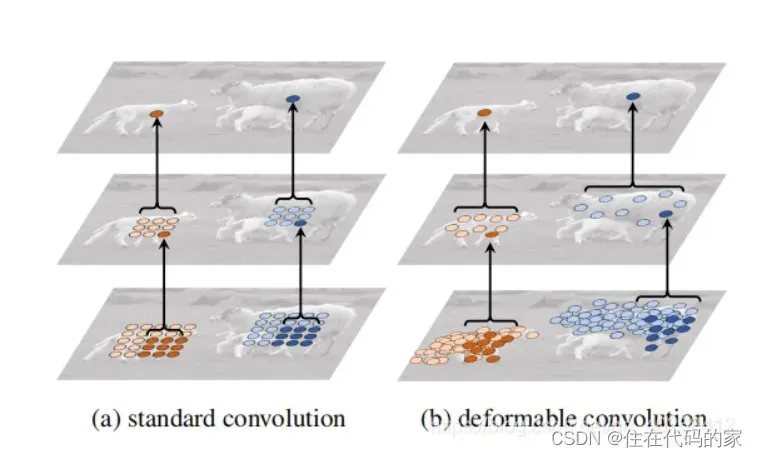
标准卷积和形变卷积卷积计算效果图对比
3.空洞卷积
定义：所谓空洞卷积就是在卷积核的元素之间添加间隔（空洞），是针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积思路。
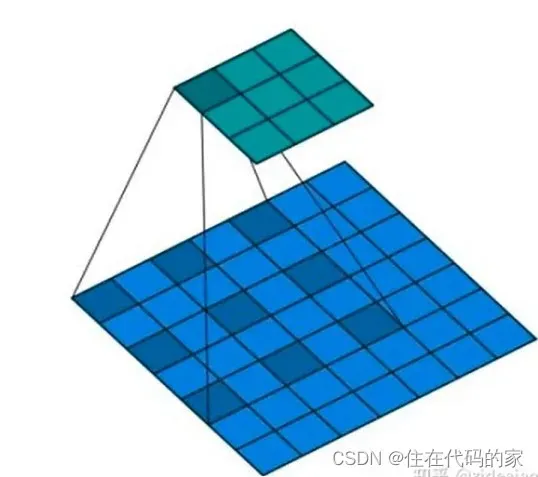
作用：要想获取较大感受野需要用较大的卷积核或池化时采用较大的stride，对于前者计算量太大，后者会损失分辨率。然而想要对图片提取的特征具有较大的感受野，并且又想让特征图的分辨率不下降太多（分辨率损失太多会丢失许多关于图像边界的细节信息），利用标准卷积是无论如何也不能兼顾的，因为二者是矛盾的。而空洞卷积就是用来解决这个矛盾的，即可让其获得较大感受野，又可让分辨率不损失太多，如下图：
空洞卷积中有个参数为rate，是用来控制卷积核元素之间间隔的大小
图一是rate = 1 的空洞卷积，卷积核的感受野为3×3，其实就是标准卷积
图二是rate = 2，padding = 2的空洞卷积，卷积核的感受野为7×7
图三是rate = 4，padding = 4的空洞卷积，卷积核的感受野为15×15
二.池化层
定义：池化层是一种子采样层，通常放置在卷积层之后，本质是对输入图像进行下采样。 池化层会将尺寸较大的特征图缩放成尺寸较小的特征图，使高层特征图获得更大的感受野。经过池化层输出的特征图仅保留输入特征图的主要的特征，降低了后续功能层运算的复杂性，因此池化层在一定程度可避免出现过拟合现象。
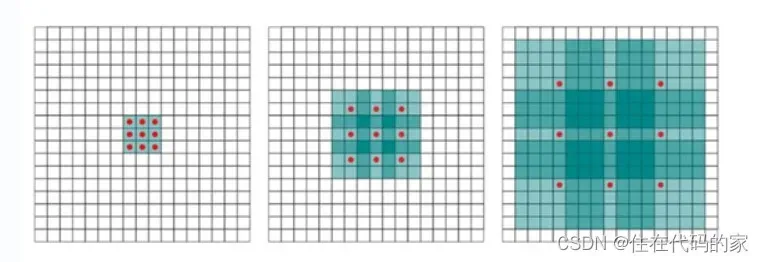
池化层主要包括最大池化层（Max pooling）和平均池化层（Average pooling）
1.最大池化层
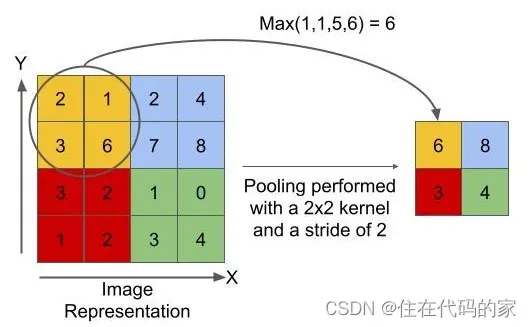
最大池化层的计算是获取滑动区域内数字的最大值作为输出结果
最大池化层能很好的保留纹理特征，一般现在都用最大池化层而很少用平均池化层
2.平均池化层
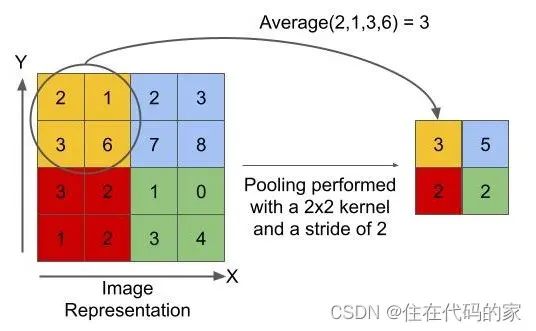
平均池化层的计算是取滑动区域内数字的平均值作为输出结果
平均池化层能很好的保留背景，但容易使得图片变模糊
三.激活函数
在神经网络训练过程中，特征之间的关系都是线性的，但现实世界是复杂的，仅凭这种简单的线性的关系是不能充分表达的，所以需要在各层网络之间添加一些非线性的成分，激活函数就起着这份作用
若想绘制各种激活函数可以查看我上一篇文章，有详细介绍，如下：
https://blog.csdn.net/mazhicheng123456/article/details/124780003?spm=1001.2014.3001.55011.Sigmoid
公式：
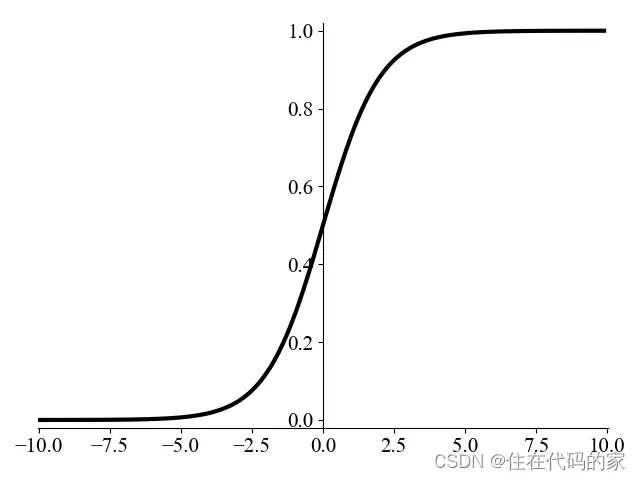
优点：函数连续光滑、处处可导、取值在0-1之间，可用在概率分布
缺点：取值在无穷时导数为零，参数得不到更新，导致梯度消失，这对于训练网络参数反向传播 时是致命的
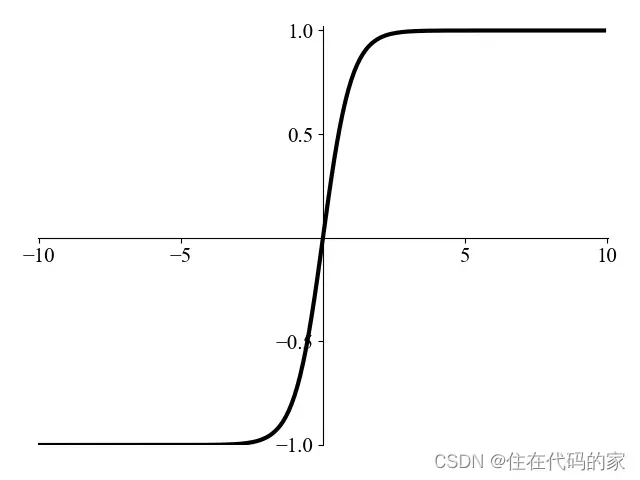
2.Tanh
公式：
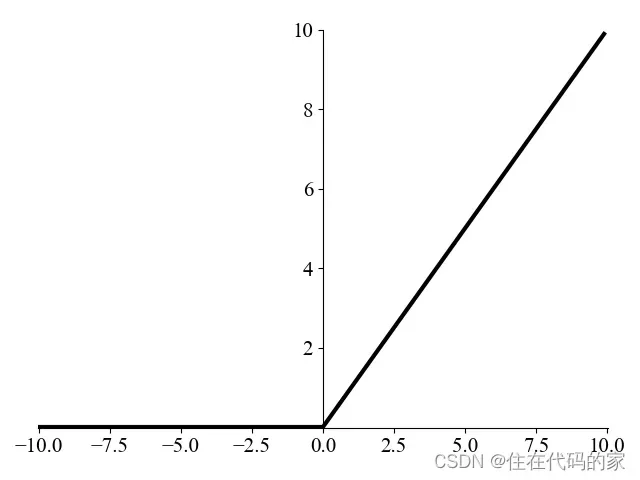
3.ReLU
公式: f(x) = 𝑚𝑎𝑥(0, 𝑥)
优点：导数固定，梯度不变，计算方便 ，计算速度快，缓解了梯度消失、爆炸的问题，适用于做 深度学习
缺点：由于负数部分恒为0，会导致一些神经元无法激活（可通过设置小学习率部分解决）
输出不是以0为中心的
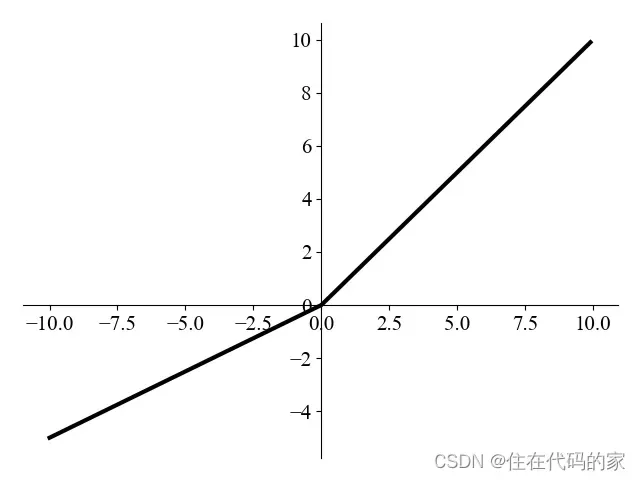
4.Leaky_ReLU
公式：f(x) = max(0,x) + leak*min(0,x)
leak是一个很小的常数，这样就保留了负轴的值，使负轴的信息不会全部丢失，是对ReLU函数的改进
Leaky_ReLU的图像：
5.Mish
公式：
其中, 是一个softmax激活函数和
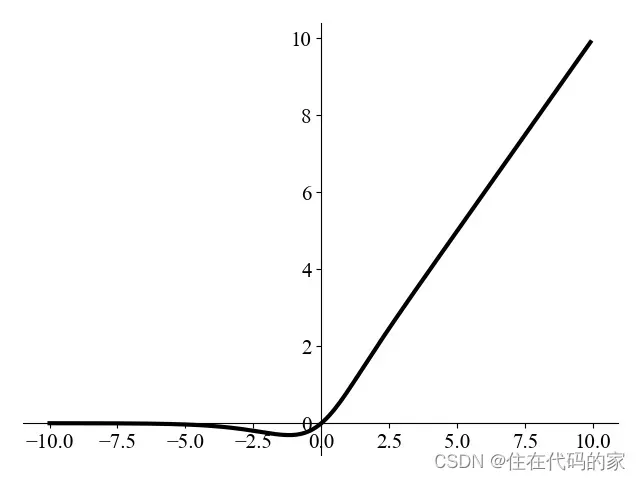
特点：曲线平滑、非单调、上无界、有下界，YOLO V4的Backbone网络中都使用Mish激活函数
四.损失函数
损失函数是神经网络中重要的一环，是一种用来计算网络预测值𝑓(𝑥)与真实值𝑌之间差异程度的函数，这种差异程度称为损失值，用符号𝐿𝑜𝑠𝑠表示。基于损失函数的作用可分为回归损失函数和分类损失函数。
1.回归损失函数
回归损失函数主要包括L1 loss、L2 loss和Smooth L1 loss，下面链接写得可参考了解学习：
2.分类损失函数
交叉熵损失函数(CrossEntropy Loss)
交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度，在机器学习中就表示为真实概率分布与预测概率分布之间的差异，交叉熵在分类问题中常常与softmax是标配，softmax将输出的结果进行处理，使其多个分类的预测值和为1，再通过交叉熵来计算损失，交叉熵的值越小，模型预测效果就越好。
公式： 
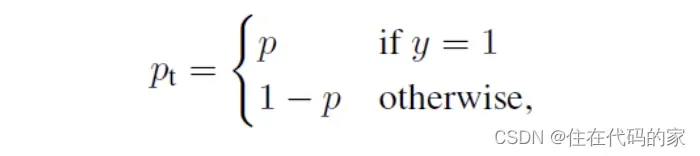
下面举例说明交叉熵损失函数是如何计算的：
假设输入一张狗的图片：
| 猫 | 狗 | 羊 | |
|---|---|---|---|
| label | 0 | 1 | 0 |
| pred | 0.2 | 0.7 | 0.1 |
那么这个网络的损失值为：
loss=−(0∗log(0.2)+1∗log(0.7)+0∗log(0.1))=0.36
平衡交叉熵损失函数（Balanced Cross Entropy）
平衡交叉熵损失函数是对交叉熵损失函数的改进，在目标检测和分类任务中要区分物体和背景，一张图片中，物体的存在是少数，这就导致正负样本极不均衡，这个损失函数正是基于这一问题提出的。
公式：
参数是平衡正负样本的，
取0~0.5之间，是增大负样本的权重，
取0.5~1之间，是增大正样本的权重
Focal Loss
面对目标检测时类别不均衡问题，何凯明等人提出了新的损失函数Focal Loss，并设计了一个网络模型RetinaNet，在同期一阶段网络速度相同的前提下，其检测精度比同期最优的二阶段网络还要高。
公式：
引入了 权重，为了改善正负样本不平衡，提高了些精度；
是为了调节难易样本的权重，当一个边框被误分类时，
接近1其损失几乎不受影响；当pt接近于1时，表明其分类结果较好，是简单样本，
接近于0，因此其损失被调低了；
是调制因子，
越大，简单样本损失越低
希望能帮到大家，如有问题可与我积极交流！
文章出处登录后可见！
