P3Depth: Monocular Depth Estimation with a Piecewise Planarity Prior
面向可解释深度网络的单目深度估计
0 Abstract
单目深度估计对于场景理解和后续任务至关重要，本文致力于改进监督方法，其中地面真值只在训练的时候使用。基于对真实3D场景高度规则性的了解，我们提出了一种学习有选择地利用共面像素信息来提升预测深度的方法。我们引入了一种分段平面性先验知识，即对于每个像素，有一个种子像素和前者共享相同的平面3D曲面。基于此，我们设计了一个两个头的网络。第一个投输出像素平面级系数，而第二个头输出密集偏移向量场，该向量场识别种子像素的位置，然后使用种子像素的平面稀疏来预测每个位置的深度，预测结果通过学习置信度自适应的和第一个头的初始预测进行融合，已解释与精准局部平面度的潜在偏差。所提方法可以实现预测规则的深度贴图，在遮挡边界处具有锋利的边缘。
1 Introduction
深度估计是计算机视觉的一个基本问题。其被广泛用于机器人视觉和自动化驾驶骑车，有相关数据表明，深度信息是执行动作和语义分割最重要的视觉水平线索。监督单目深度最主要的问题是尺度模糊，因为相同图像的输入具有无限多3D场景的生成。
目前解决这项任务的的趋势是使用完全卷积的神经网路哟啊来输出密集的深度预测，常用的方法有标准的监督深度和基于重建视图的自监督单目深度估计。目前大多数监督方法都是基于像素级的损失约束，这种方法忽略了3D世界的高度规则性，会生成分段平滑的深度贴图。
对3D世界几何结构最常见的模型是采用平面描述，平面是局部可微深度图的局部一节泰勒近似，可以很容易的采用三个独立的系数进行参数化描述。一旦像素和平面相关联，改像素的深度可以从关联平面的系数中恢复，在一些方法中，这样的平面系数可以用来预测学习表示平面。
本文采用了上述的平面表示方法，但本文并不是并不是用其来进行显式的平面预测，而是用该方法来作为基于平面性的先验知识，以定义像素之间的交互适当输出空间。本文网络的第一个头部用来输出密集的平面系数，然后将其转化为深度图。在理想情况下，属于同一平面上的两个像素点应该具有相同的平面系数和不同的深度。因此，如果p，q处以同一个平面，使用p的平面系数来预测q的深度应该是正确的结果。（呃。。。为什么不直接用q的平面系数来预测q的深度呢，只是单纯的为了增加约束吗）
我们通过学习识别与检测像素共享同一平面的种子像素来利用这一特征。这种方法是由一种分段平面性先验知识来驱动的。对于关联3D平面的每一个像素p，在p的领域内存在一个种子像素q，像素q与像素p的平面相关。为了使用上述特性，我们需要预测p-q之间的便宜量来识别（1）先验知识有效的区域（2）区域内的种子像素。因此，我们设计了第二个网络头，用来输出密集向量偏移图和置信度图。预测的偏移用于对来自第一头部的平面系数进行重采样，并生成第二深度预测。然后，使用置信图来作为权重参数进行两个深度预测的融合权重，并主要依赖于分段平面性先验无效区域的基本深度预测。最后，我们提出了一个平均平面损失，用来加强我们预测的3D曲面和真实世界的一阶一致性。
2 Related work
监督单目深度估计是假设地面真值可以用来训练，通过对单幅图像进行推理来预测深度信息。早期的方法是Mark3D，它在场景中手工绘制了一个分段平面结构，并使用马尔可夫随机场局部学习相关参数。Eigen提出的多尺度网络通过学习从图像到深度图的端到端映射，率先在深度图中使用cnn。目前的研究工作主要在一下几个方向。（1）更先进的网络结构，例如残差网络，卷积神经场、频域多尺度融合登。（2）更适合深度损失的约束，如反向Huber损失、分类损失、顺序回归损失、成对排序损失登。（3）使用法线和语义标签联合学习深度。我们的方法属于这一类，通过利用场景的规律性来讲深度信息投放到合适的位置。其他深度话估计包括无监督和半监督的深度估计以及基于立体的深度估计。（下面是一些方法的描述，此处略过）几何先验知识受到了广泛的关注，分段平面性先验知识传统上用于多视图立体和三维重建。这些方法设计显式深度平面，并将这些平面拟合到3D点云的超像素上。
3 Method
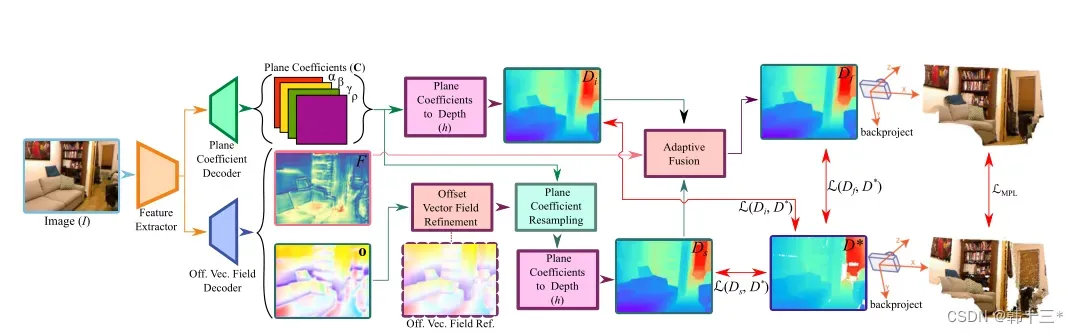
一个编码器对应两个解码器，第一个解码器用来预测平面系数，并通过平面系数得到深度图Di,第二个解码器输出密集像素偏移量O和置信图F，通过细化偏移量后查找种子像素，并通过种子像素的平面系数来预测深度图Ds,通过置信图F将深度图Di和Ds进行加权融合得到深度图Df,将深度图Di，Ds和Df与真值D*进行损失计算，构建约束。
本文网络通过选择性地组合每个像素和种子像素的深度来估计深度，本文采用了一种平面系数表示来实现像素深度和平面信息的通用表示法，并推到了平面系数和深度信息之间的解析关系。平面系数表示法的主要优点是，假设两个像素位于同一个平面上，可以通过不同像素的平面系数直接计算像素中的深度信息。最后本文提出了一个面片级的平均平面损失，有助于网络独立学习规则深度图。
监督深度估计可以看作是从二维像素中预测深度信息，其种I（u，v）为图片，D(u,v)为其对应的深度图，fθ为映射过程，其中θ为参数，T为训练集，L为损失函数，用来约束预测和实际图片D*之间的偏差，整体过程可以描述为以下公式。
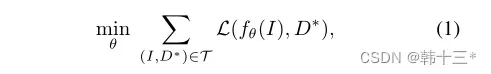对于一个给定深度图D（u，v）的图片,我们可以采用反向投影将每个像素点投影到3D空间，例如，给定焦距fx,fy和主点（u0，v0），每个像素p（u，v）的三维点P（X，Y，z）满足如下条件。
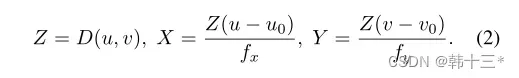
假设反向投影的3D点P对应3D场景的平面部分，点-法形式中的关联方程可以写成nP+d=0，其中n=（a，b，c）为平面的法向量，d为该点到平面的距离。将P点坐标带入公式后可以得到以下公式。
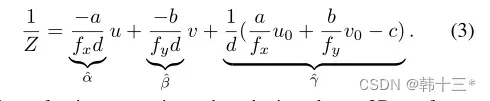
通过公式简化后可以得到如下公式，其中α, β, γ, ρ都是和平面相关的参数，所以引入C=（α, β, γ, ρ），将C称为平面系数，所以深度信息Z=h（C，u，v），其中h为映射函数。
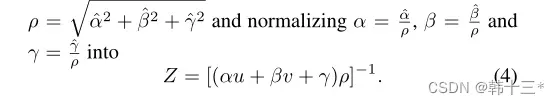
本文并不是直接预测深度，且预测平面信息的间接方式也不会带来直接优势。但位于统一平面的两个像素，往往具有相同的平面系数C，但是具有不同的深度，这使得我们可以采用种子像素的平面系数来预测目标像素的深度。
我们假设像素p位于3D空间的平面上，这个平面都有相同的C，在理想的情况下，我们只需要预测一个像素q就可以计算出平面上的所有深度，这个像素q被描述为种子像素，为了准确的定义种子像素和其相同深度的区域，我们使用神经网络来完成这一过程。
基于分段平面性先验，对于具有关联平面的像素点p，在其领域内存在一个种子像素点q，该点也和平面相关联，定义p，q之间的偏移量为O（p）=p-q，由于p，q具有相同的平面系数，所以就要C（p）=C（q），即C（p）=C（p+O（p）），通过双线性插值可以得到重新采样的平面系数计算深度预测的公式如下所示。
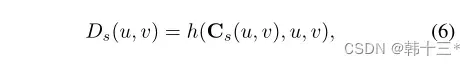
然而基于种子位置的深度信息并不都是准确的，所以第二个编码器也输出了置信图F∈[0,1],最终的深度图由两个深度图加权得到。
平均平面损失如下。
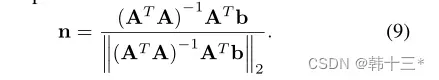
4 Experimental results
NYU数据对比。
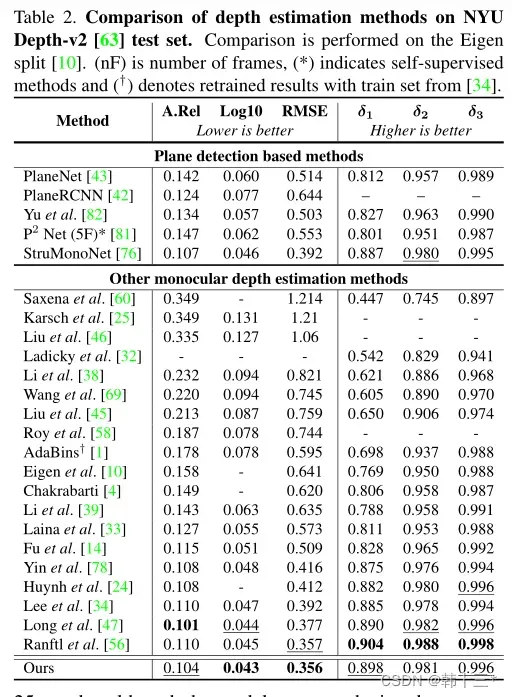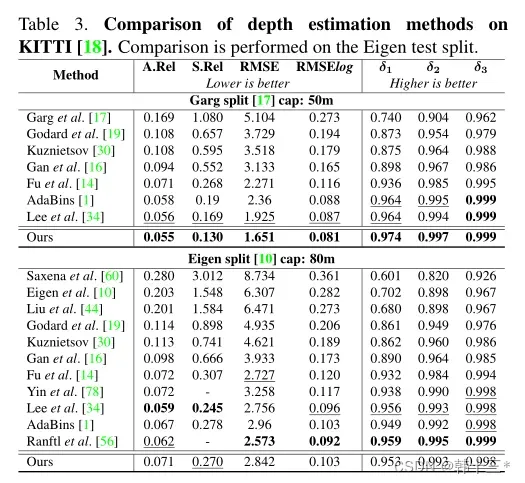
Kitti数据对比。
文章出处登录后可见！
