一、背景

数据驱动建模通常与理论驱动建模相对，但它们的集成也被认为是一种重要的方法，称为灰盒或混合建模。机器学习中的灰盒/混合建模在学习鲁棒模型方面具有相当大的前景，具有改进的外推能力，超出了它们在训练期间接触到的分布。此外，就模型可解释性而言，它可以带来显著的好处，因为模型的部分在语义上基于具体的领域知识。

将物理模型集成到机器学习中已经在各种情况下被考虑过(例如[44,40]和本文的第4节)，但现有的大多数研究都集中在预测或预测任务上，不能直接适用于其他任务。更重要的是，对基于物理和数据驱动的组件的精心编排没有加以考虑。

这篇文章的目标是整合不完整的物理模型到深度生成模型。在本文的VAE中，解码器由基于物理的模型和可训练的神经网络组成，其中一些潜在变量以物理模型的参数为语义基础。这种VAE，如果经过适当的训练，从理论上讲是可以部分解释的。此外，本文提出了一个正则化的学习框架，以确保物理模型的有意义的使用，并在物理集成的VAEs中保留潜在变量的语义。经验表明，本文的方法可以学习一个具有更好的泛化性的模型，更重要的是，可以在非分布情况下进行稳健的外推。

二、Physics-integrated VAEs模型框架

首先假设物理模型可以用合理的代价来解析或数值求解，并且(近似)解对于解所依赖的量是可微的。另外，为了便于讨论，假设一个VAE解码器由两部分组成：物理模型 $f_P$ 和可训练辅助函数 $f_A$ 。

2.1、潜在变量和先验

考虑两种潜在变量： $z_P$ 和 $z_A$ ，分别用于 $f_P$ 和 $f_A$

$p(z_P):=\mathcal{N}(z_P|m_P,v^2_PI)\ \ and\ \ p(z_A):=\mathcal{N}(z_A|0,I)$

其中 $m_P$ 和 $v^2_P$ 是根据fp参数的先验知识定义的。

2.2、解码器

解码器包含两种类型的函数： $f_P:\mathcal{Z}_P\rightarrow \mathcal{Y}_P\ \ and\ \ f_A:\mathcal{Y}_P\times \mathcal{Z}_A\rightarrow \mathcal{Y}_A$ 。为了便于标记，考虑一个函数 $\mathcal{F}$ ，它计算 $f_P$ 和 $f_A$ ，如果有方程，则解一个方程，得出观测x(x可以是序列，图像等等)。用函数 $\mathcal{F}$ 表示解码过程，其参数为 $f_P$ 和 $f_A$ 以及z，即 $\mathcal{F}[f_P,f_A;z_P.z_A]$ 。在 $\mathcal{F}$ 内部，函数可以通过各种方式连接， $\mathcal{F}$ 可以包括

(1)in-equation augmentation solve $(f_P + f_A = 0)$ or solve $(f_A\circ f_P = 0)$ .

(2)out-equation augmentation $f_A(solve(f_P = 0))$ .

(3)它们的任意组合，即， $f_{A,3}(solve(f_{A,2}(f_P + f_{A,1}) = 0))$ .

2.3、编码器

编码器包含两部分： $z_P$ 的后验推断和 $z_A$ 的后验推断。考虑以下对近似后验的分解:

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ q_\psi (z_P, z_A | x) := q_\psi (z_A | x)q_\psi (z_P | x, z_A), \\ where\ \ q_\psi (z_A | x):=\mathcal{N} (z_A | g_A (x), \Sigma _A),q_\psi (z_P | x, z_A):=\mathcal{N} (z_P | g_P (x,z_A), \Sigma _P)$ .

$g_A : \mathcal{X} \rightarrow\mathcal{Z}_A$ 和 $g_P:\mathcal{X}\times \mathcal{Z}_A\rightarrow \mathcal{Z}_P$ 是识别网络。

2.4、Evidence lower bound

$ELBO(\theta, \psi ; x) = E_{q_\psi}(z_P,z_A|x) log\ p_\theta(x | z_P, z_A)- \\ \ \ \ \ \ \ \ \ \ \ D_{KL}[q_\psi(z_A | x)||p(z_A)] - E_{q_\psi}(z_A|x)D_{KL} [q_\psi (z_P | x, z_A)||p(z_P)]$

三、正则化：在物理模型和可训练模型之间取得平衡

本文提出了一个正则化的学习目标，用于物理集成的VAEs。它包括两种类型的正则器。第一个是正则化函数近似器(如神经网络)不必要的灵活性；第二个是接地编码器输出物理参数。

3.1、可训练函数的过剩灵活性正规化

作者认为，如果物理集成VAE的可训练成分(即 $f_A$ )具有丰富的表达能力，就像深度神经网络通常的情况一样，仅仅最大化ELBO并不能保证基于物理的组件(即 $f_P$ )将以有意义的方式使用;例如 $f_P$ 可能会被忽略。

为了确保 $f_A$ 不会不必要地支配整个模型的行为， $f_P$ 也不会被忽略，作者借鉴了后验预测检验(PPC)的思想，这是一种检验统计模型有效性的程序。标准ppc检查的是模型和数据分布之间的差异，而本文计算的是模型和它的“纯物理”简化版本之间的差异，下面提出的正则化就是为了最小化这个差异。

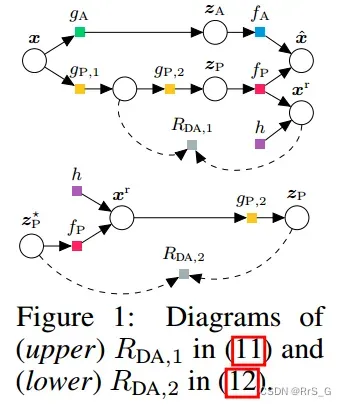
首先给出“纯物理”简化版本的定义：解码器用一个基函数 $h_A : \mathcal{Y}_P\rightarrow \mathcal{Y}_A$ 替换了原始模型中的 $f_A:\mathcal{Y}_P\times \mathcal{Z}_A\rightarrow \mathcal{Y}_A$ ，解码过程为 $\mathcal{F}[h_A, f_P; z_P]$ ，省略掉了 $z_A$ ，因此相关的编码器直接使用了先验 $p(z_A)$ ，具体为 $q^r_\psi (z_A, z_P | x) := p(z_A)\int q_\psi (z_P, z_A | x)dz_A$ 。

有了模型，然后为了最小化两个版本之间的差异即最小化两个后验预测分布的差异，即最小化下面的式子：

$D_{KL} [p_{\theta,\psi}(\widetilde{x}| X) || p^r _{\theta^r,\psi }(\widetilde{x} | X)]$ .

解析计算上式通常是棘手的。因此，取其上界，具体如下。

$D_{KL}[p_{\theta,\psi}(\widetilde{x}|X) || p^r_{\theta^r,\psi}(\widetilde{x}|X)]\leq \\ \mathbb{E}_{p_d (x|X)}[\mathbb{E}_{q_\psi(z_P,z_A|x)}D_{KL}[p_ \theta || p^r_ \theta ] + D_{KL}[q_ \psi(z_A|x) || p_A] + \mathbb{E}_{q_ \psi (z_A|x)}D_{KL}[q_ \psi (z_P|z_A,x) || p_P]]$ .

用 $\mathbb{E}_{p_d (x|X)}\hat{D}(\theta,param(h),\psi;x)$ 表示上式右边项，即上界。则抑制可训练函数不必要灵活性的正则化就定义为下式的最小化：

$R_{PPC}(\theta,param(h),\psi) := \mathbb{E}_{p_d (x|X)}\hat{D}(\theta,param(h),\psi;x)$

3.2、基于物理数据增强的接地物理编码器

作者认为，为了正确学习物理集成的VAEs，只最小化 $R_{PPC}$ 可能不够,因为推断 $z_P$ 可能仍然毫无意义但让 $R_{PPC}$ 不是很大，然后优化可能无法逃脱局部最小值。为此，作者提出以下解决方案。

该方案思想是使用物理模型作为数据扩充的信息源，这有助于将PI-VAE中的识别网络 $g_P$ 的输出与 $f_P$ 的参数联系起来。作者想要采样一些 $z_P$ ，将其提供给物理模型 $f_P$ (以及一个求解器)，并在训练期间使用生成的信号作为额外数据。实现这一目标的一个技术挑战是，由于物理模型可能不完整，它产生的人工信号和真实信号可能具有不同的性质。

首先为了弥补这种差异，作者安排了一个物理编码器 $g_P$ 的特殊功能：让 $z^*_P$ 表示从先验 $p(z_P)$ 中抽取的样本，然后通过向上述纯物理简化模型当中输入 $z^*_P$ 生成 $x^r(z^*_P)$ ，也就是 $x^r(z^*_P) := \mathcal{F}[h_A,f_P;z_P = z^*_P]$ 。

然后，作者希望在给定相关 $x^r(z^*_P)$ 的情况下，识别网络 $g_P$ 可以成功估计出 $z^*_P$ ，这就说明，由 $g_P$ 推断的结果是基于 $f_P$ 的参数的。

但是，一般来说，真实数据x和增强数据 $x^r(z^*_P)$ 具有不同的性质，因为 $f_P$ 可能会错过真实数据生成过程的某些方面。针对这一问题，作者考虑了识别网络 $g_P$ 的具体设计：将 $g_P$ 分解为两个阶段，即 $g_P(x, zA) = g_{P,2}(g_{P,1}(x, z_A))$ ，一方面， $g_{P,1}$ 应该将真实数据x转换为类似于基于物理的增强信号 $x^r$ ，换句话说， $g_{P,1}$ 应该将真实数据“净化”成虚拟的“纯物理”版本，作者通过使其输出接近以下值来执行 $g_{P,1}$ 的这种功能，即 $x^r(g_P(x,z_A))=\mathcal{F}[h_A,f_P;z_P=g_P(x,z_A)]$ 。另一方面， $g_{P,2}$ 应该接收这种“清理”的输入，并返回 $z_P$ 的后验分布。如果 $g_{P,1}$ 的功能成功实现，那么就可以使用 $x^r(z^*_P)$ 对 $g_{P,2}$ 进行自我监督，因为这时候 $x^r(z^*_P)$ 和 $x^r(g_P(x,z_A))$ 应该有相似的性质。

综上所述，作者定义了一对正则器来设置 $g_{P,1}$ 和 $g_{P,2}$ 的功能，如下所示：

定义：设sg[·]为停止梯度算子。基于物理的数据增强的正则化定义为最小化

$R_{DA,1}(\psi):=\mathbb{E}_{p_d (x|X)q(z_A|x)}||g_{P,1}(x,z_A)-sg[x^r(g_P(x,z_A))]||^2_2$ and

$R_{DA,2}(\psi):=\mathbb{E}_{z^*_P}||g_{P,2}(sg[x^r(z^*_P)])-z^*_P||^2_2.$

对应的计算示意图如下图所示：

3.3、整体规划的学习目标

本文提出的物理集成VAEs的整体正则化学习目标如下:

$\min_{\theta,param(h),\psi}-\mathbb{E}_{p_d (x|X)}ELBO(\theta,\psi;x)+\alpha R_{PPC}(\theta,param(h),\psi)+\beta R_{DA,1}(\psi)+\gamma R_{DA,2}(\psi)$

文章出处登录后可见！

已经登录？立即刷新

Physics-Integrated Variational Autoencoders forRobust and Interpretable Generative Modeling