训练深层神经网络是十分困难的,特别是在较短的时间内使他们收敛更加棘手。 在本节中,我们将介绍批量规范化(batch normalization),这是一种流行且有效的技术,可持续加速深层网络的收敛速度,但一般不改变模型精度。
为什么需要使用批量归一化呢?
总结来说:使用浅层模型时,随着模型训练的进行,当每层中参数更新时,靠近输出层的输出较难出现剧烈变化。而对深层神经网络来说,随着网络训练的进行,前一层参数的调整使得后一层输入数据的分布发生变化,各层在训练的过程中就需要不断的改变以适应学习这种新的数据分布。所以即使输入数据已做标准化,训练中模型参数的更新依然很容易导致后面层输入数据分布的变化,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去,最终造成靠近输出层输出的剧烈变化。这种计算数值的不稳定性通常令我们难以训练出有效的深度模型。如果训练过程中,训练数据的分布一直在发生变化,那么将不仅会增大训练的复杂度,影响网络的训练速度而且增加了过拟合的风险。
批量归一化应用于单个可选层(也可以应用到所有层),其原理如下:在每次训练迭代中,我们首先规范化输入,即通过减去其均值并除以其标准差,其中两者均基于当前小批量处理。 接下来,我们应用比例系数和比例偏移。
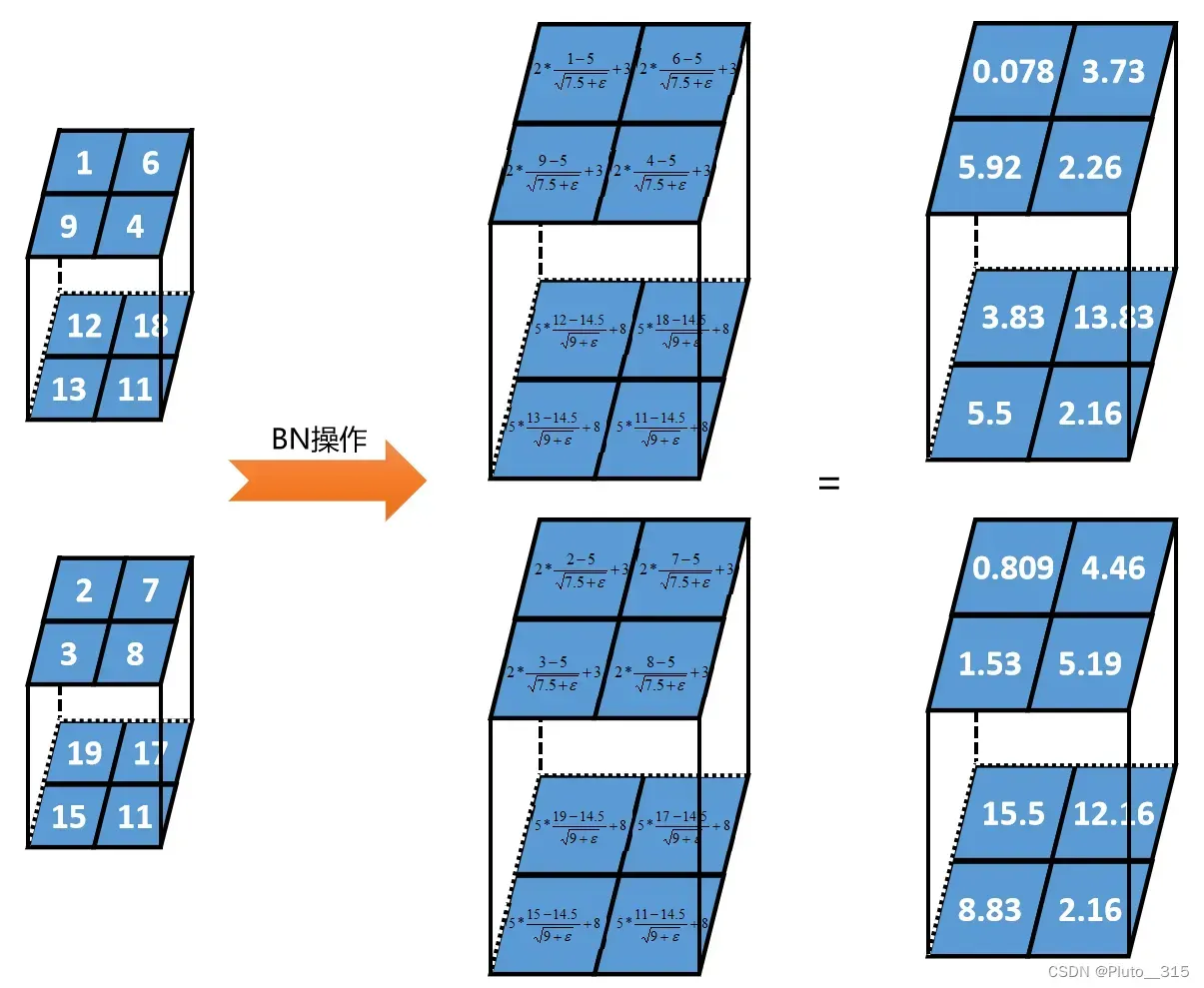
在模型训练时,在应用激活函数之前,先对一个层的输出进行归一化,将所有批数据强制在统一的数据分布下,然后再将其输入到下一层,使整个神经网络在各层的中间输出的数值更稳定。从而使深层神经网络更容易收敛而且降低模型过拟合的风险。
批量归一化的优势:
- 使得后一层网络不必不断去适应底层网络中输入的变化,从而实现了网络中层与层之间的解耦,允许每一层进行独立学习,有利于提高整个神经网络的学习速度。
- 可以选择比较大的初始学习率,无需慢慢调整学习率,学习率的衰减速度也很大。
- 改善正则化策略:作为正则化的一种形式,轻微减少了对dropout的需求。
- 可以把训练数据彻底打乱,提高网络泛化性能。神经网络学习过程本质上就是为了学习数据分布,如果训练数据与测试数据的分布不同,网络的泛化能力就会严重降低。
- 随着网络深度加深或者在训练过程中,特征输入值整体分布逐渐往非线性函数的取值区间的上下限两端靠近,这会导致反向传播时低层神经网络的梯度消失,BN就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布,可以缓解S型激活函数反向传播中的梯度消失的问题。
批量规范化和其他层之间的一个关键区别是,由于批量规范化在完整的小批量上运行,因此我们不能像以前在引入其他层时那样忽略批量大小。 下面讨论这两种情况:全连接层和卷积层,他们的批量规范化实现略有不同。
如果批量归一化作用在全连接层,那么它是作用在特征维,比如shape (batchsize, features_num) 那么求均值后就是(, features_num)。批量归一化是对批量进行归一化,而不是一个样本里的特征做归一化。而批量归一化在卷积里面是作用在通道维的。因为卷积的shape是 (batchsize, channel, height, width) 这里的每一个channel实际上就是一个特征维度。
全连接层
通常,我们将批量规范化层置于全连接层中的仿射变换和激活函数之间。 设全连接层的输入为u,权重参数和偏置参数分别为W和b,激活函数为ϕ,批量规范化的运算符为BN。 那么,使用批量规范化的全连接层的输出的计算详情如下:
h=ϕ(BN(Wx+b)).
卷积层
同样,对于卷积层,我们可以在卷积层之后和非线性激活函数之前应用批量规范化。假设我们的小批量包含m个样本,并且对于每个通道,卷积的输出具有高度p和宽度q。 那么对于卷积层,我们在每个输出通道的m⋅p⋅q个元素上同时执行每个批量规范化。 因此,在计算平均值和方差时,我们会收集所有空间位置的值,然后在给定通道内应用相同的均值和方差,以便在每个空间位置对值进行规范化。
预测时的批量归⼀化
训练:以batch为单位,对每个batch计算均值和方差。
预测:用移动平均估算整个训练数据集的样本均值和方差。
小结
- 在模型训练过程中,批量规范化利用小批量的均值和标准差,不断调整神经网络的中间输出,使整个神经网络各层的中间输出值更加稳定。
- 批量规范化在全连接层和卷积层的使用略有不同。批量归一化作用在全连接层,那么它是作用在特征维;批量归一化在卷积里面是作用在通道维的。
- 批量规范化层和暂退层一样,在训练模式和预测模式下计算不同。在训练时,是对每一批的训练数据进行归一化,也即用每一批数据的均值和方差。 而在测试时,比如进行一个样本的预测,就并没有batch的概念,因此,这个时候用的均值和方差是全量训练数据的均值和方差,这个可以通过移动平均法求得。
文章出处登录后可见!
