矩阵A可以LU分解的充要条件是
.
如果矩阵A可以LU分解, 分解的唯一性需要通过下式分析
,
.
下面给出一个分解算法.
- INPUT
- FOR
DO
- IF
THEN
- ELSE
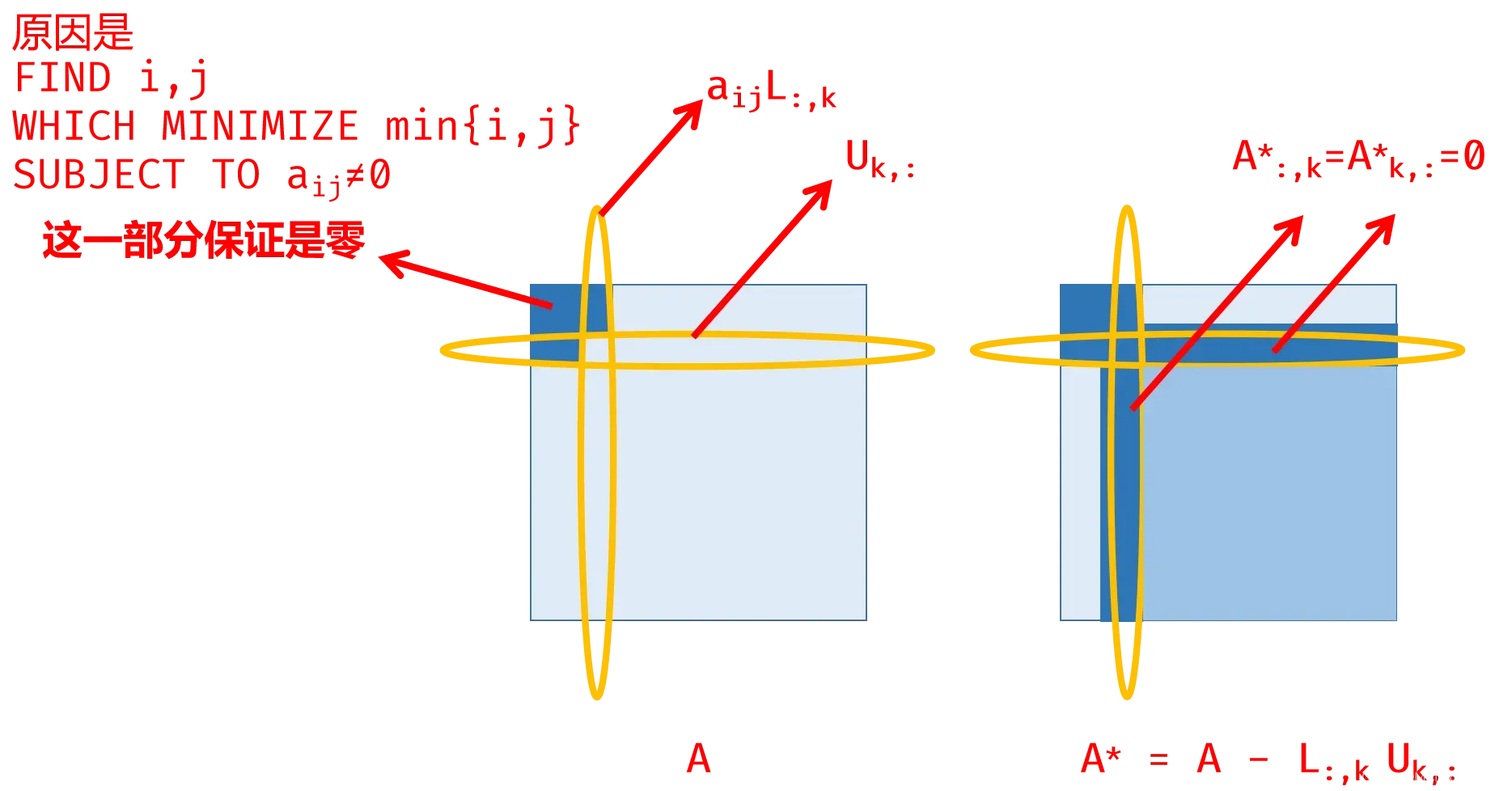
- FIND
WHICH MINIMIZE
SUBJECT TO
- END IF
- END FOR
- OUTPUT
,
,
参考文献
Pavel Okunev, Necessary And Sufficient Conditions For Existence of the LU Factorization of an Arbitrary Matrix.
书上的定理7.3是
矩阵A可以LU分解的充分条件是
的顺序主子式
(
)
此时分解是唯一的.
文章出处登录后可见!
已经登录?立即刷新
