本文资料来源(配图):EMPossible_CEM
1、课件资料:https://empossible.net/academics/emp5337/
2、视频资料:
youtube:https://www.youtube.com/watch?v=JOgtCeUMIAc
bilibili:https://www.bilibili.com/video/BV1ck4y1m73u?p=2
一、电磁场中的一维结构
将三维结构降为一维结构:
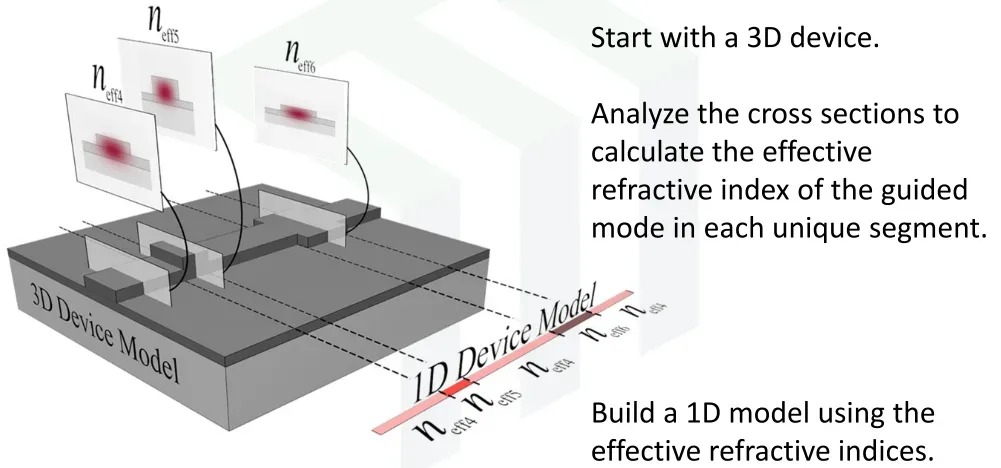
二、传递矩阵法
1、模型结构
模型结构的建立是基于上一节的内容,也就是通过将三维结构降为一维结构来进行分析的,类似于切片的方法。如下图所示,假设有一束光打在由四层介质板构成的器件上。
将Layer1最靠前一侧的界面0(z=0处)的电磁场定义为E0和H0,将Layer1靠后一侧的界面1的电磁场定义为E1和H1。当发射电磁波时,对于这个器件而言,我们假设电磁波是从界面0出发,经过Layer1后,到达界面1的,因此若要建立起两个界面电磁场之间的关系,关键就在于对Layer1层的分析。
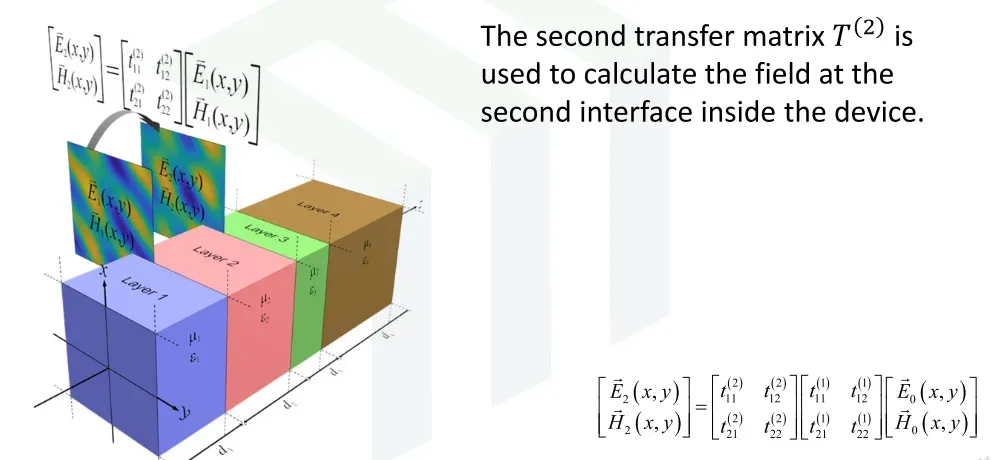
而传输矩阵(Transfer Matrix,通常称为T矩阵),就是我们用来构建起两个界面电磁场之间关系的一个矩阵,即E0和H0经过T矩阵的变换后变为了E1和H1,也由此我们可以认为:事实上,T矩阵是表征了Layer1自身的一些属性(如:电导率、磁导率等)对电磁波产生的影响。
基于此,我们可以用一个简单的公式来表示两个界面电磁场间的关系,即:[E1, H1]=T1 • [E0, H0],T为矩阵;同样地,对于界面2的电场E2和界面1的电场E1,我们也可以获得关系式:[E2, H2]=T2 • [E1, H1]=T2 • T1 • [E0, H0],即如上图所示。
按照以上的方法,对整个器件涉及到的界面关系均进行推导,我们即可以获得输入界面和输出界面之间的电磁场关系,如下图所示。对于该关系中所有涉及到的T矩阵的累乘,我们将之称为全局传输矩阵(Global Transfer Matrix)。

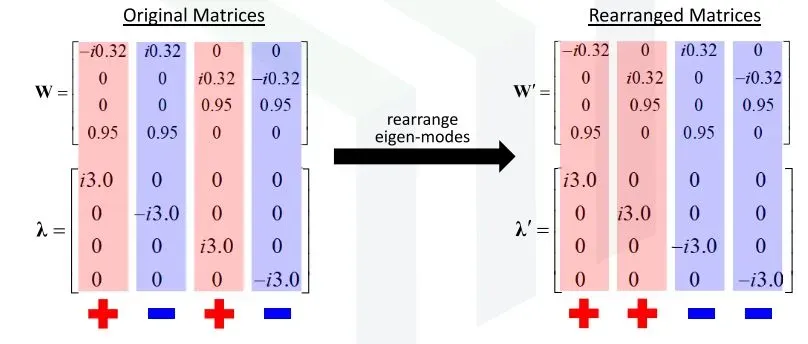
此时问题的关键,就变为了要如何推导出T矩阵? 这里,我们先给出结果(下图),再对过程进行分析。由下图可以看出,有两种方法可以获取最终的解,一种方法是需要 sort(分类)的,在这个方法过程中需要使用到4×4矩阵;另一个方法是不需要 sort 的,其使用到的是2×2矩阵。
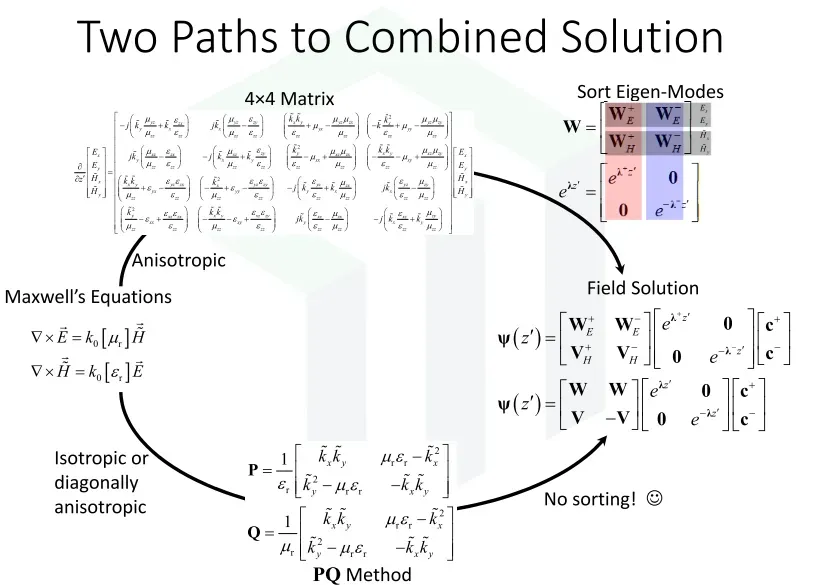
2、4×4矩阵方法(需要sort)
(1)前提内容
在均匀介质中,假设电磁波的入射方向是 +z 方向,则: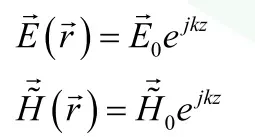
同理,在均匀介质中,假设电磁波的入射方向是 方向,则:
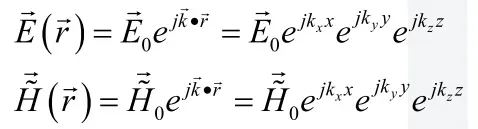

但由于沿z方向结构的非均匀性,故而其不能直接进行求导:
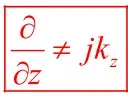
(2)4×4矩阵方程式(用于求解电磁场方程)
在 Lecture 1 学习笔记 (1) 中,通过对麦克斯韦方程组的变形和展开,得到了一组关于 E 和 H 在三个方向的等式,它们是通常用于计算电磁学中的麦克斯韦方程组,我们将之称为Starting Point for CEM,即:
需要注意的是:这些等式对应的是LHI的情况( []=
,[
]=
)
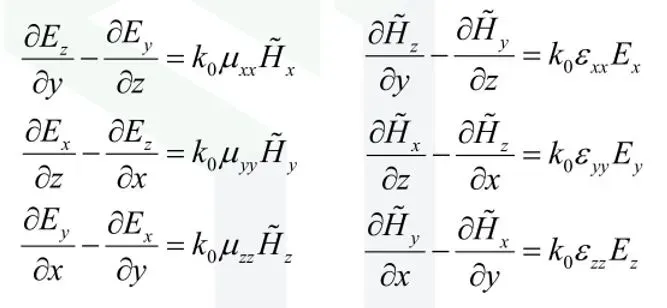
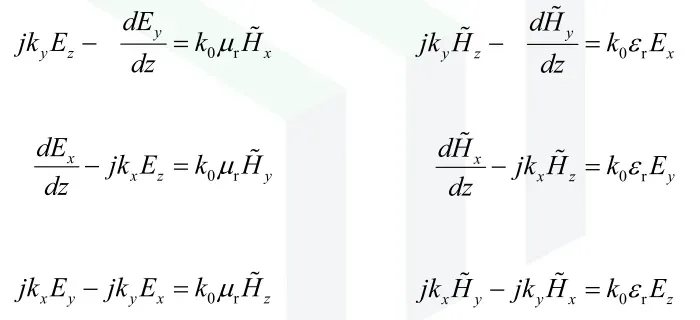
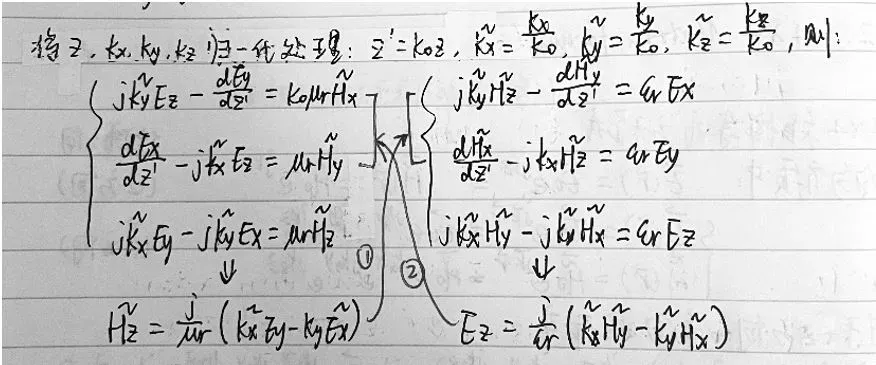
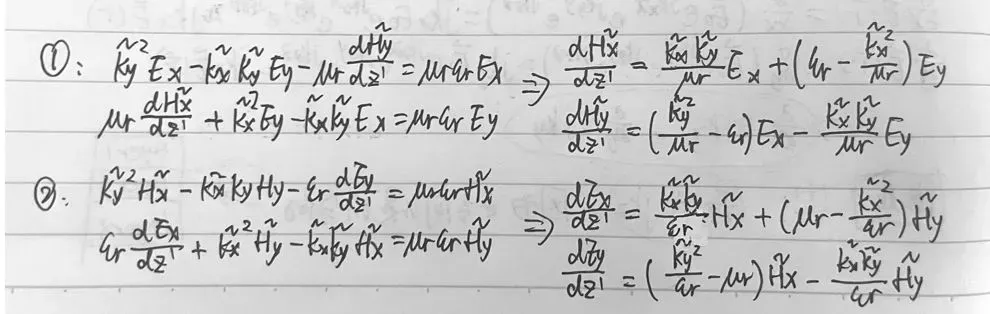
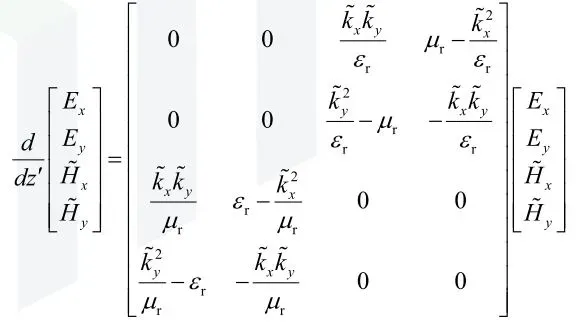
(3)LHI 情况下的解
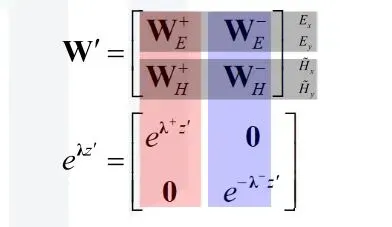
将上式的表达形式进行简化:
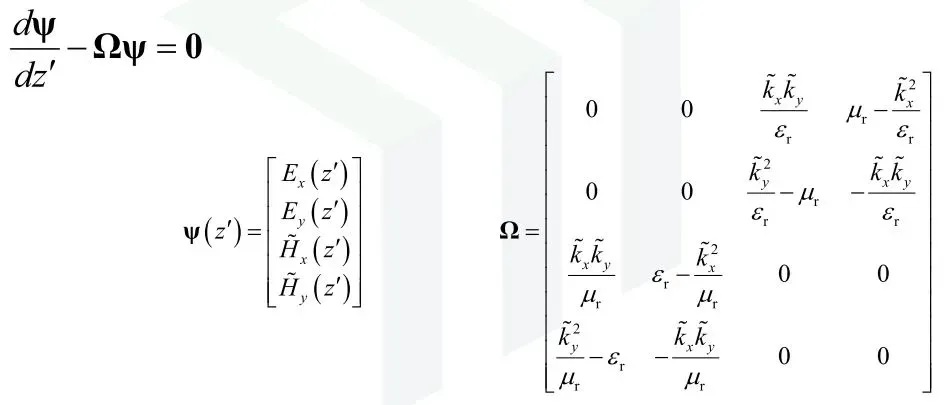
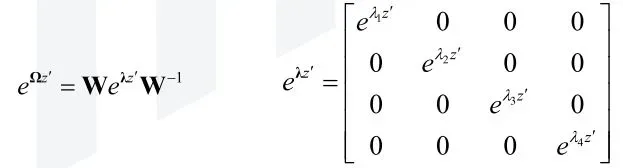
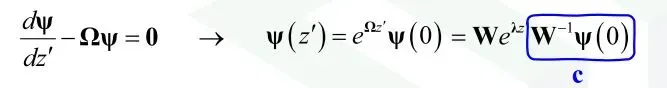
(4)计算传输矩阵T
在获取到电场和磁场的表达式后,需要引入边界条件来对器件边界情况进行一个约束。
根据器件建立的模型(如下图所示),以Layer i 为例,其存在左右两个界面,因此有两个边界条件,再将表达式代入,可以得到:
① ——->
① ——->
由于,因此可以得到变换矩阵
:
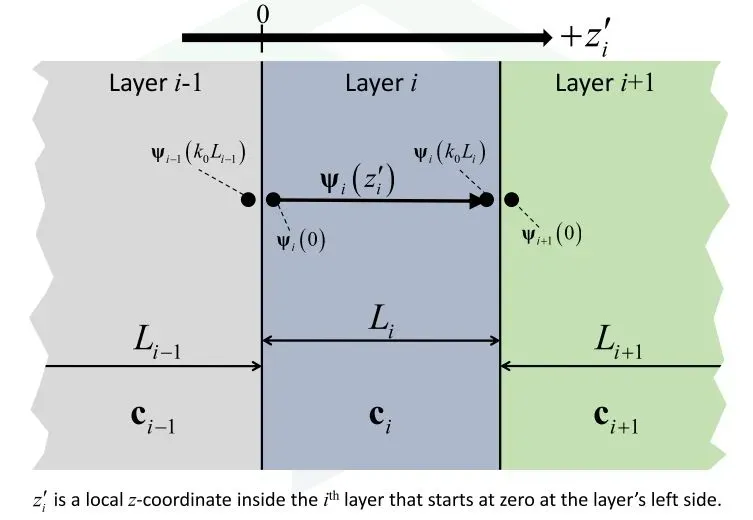
(5)稳定性问题
我们从麦克斯韦方程组开始,推导出了用来表征电磁场随变化情况的场方程等式;而后使用一阶微分方程通解公式和矩阵性质,求出了该场方程的表达式;随后,利用各层之间的边界条件对各界面进行约束,求解出了传输矩阵 T。虽然看起来已经求得了我们需要的结果,但事实上,我们通过该方法得出的结果是不稳定的,或者说这个模型是不稳定的。
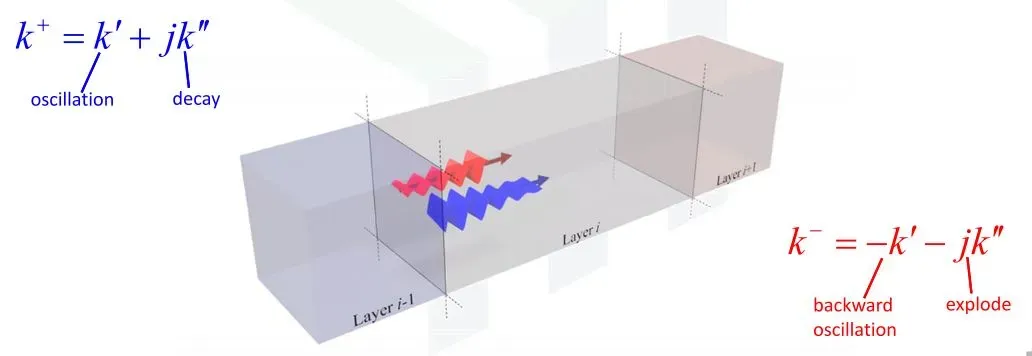
在一开始,我们写平面波的电场和磁场方程的时候,我们将其入射方向设为的是,但是k波矢通常是一个复数。对于前向传播(forward propagation)的电磁波来说,其可以展开为
;对于反向传播(backward propagation)的电磁波来说,其可以展开为
,其中
表现为波的振荡,
表现为波的衰减或增强,这两种波都会存在于实际的器件层中,如下图。
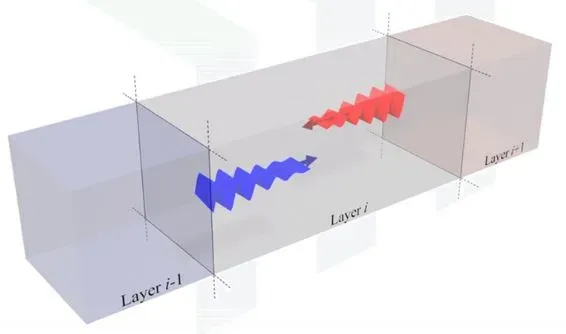
但是在我们的模型中,是默认所有波为前向传播的,因为我们的方程是:(前向),而没有考虑到
(反向)。所以,为了让反向波能够像前向波一样被处理,我们将
的表达式变为:
,如下图所示。如果我们假设原来的
是衰减的,那么
在指数上则是成增长的态势,是非常不稳定的。
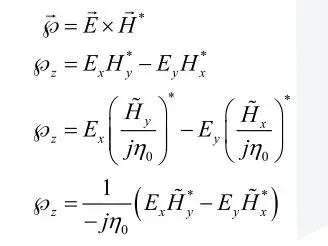

如有错误,欢迎指正…
文章出处登录后可见!
