【Applied Algebra】求解布尔方程(Boolean Equations)的4个高效baseline算法

求解布尔方程(Boolean Equations)的4个高效baseline算法

求解布尔方程(Boolean Equations)是理论计算机中的基本问题之一;事实上,求解上个变量的个非线性多项式方程组是一个基础的数学问题,受到了包括密码学界在内的各个理论计算机研究方向的广泛关注;众所周知,AI领域的计算机视觉和自然语言处理就有许多具体任务(比如人脸识别,语义分割)的baselines(也就是提供参考对比的基线模型/算法),那么自然研究求解布尔方程也有对应的baselines,今天我们就介绍当前最佳的4个高效baseline算法.

布尔方程组求解问题(Boolean PoSSo (polynomial system solving) Problem):给定一组布尔多项式:

目标是找到解 对于 , 满足 . 其中:

它限定了每个变元的取值也在 上;

算法分类

布尔方程组求解问题和计算机科学里的许多其他 NP-hard 问题都有联系(比如SAT问题,MILP整数规划问题等等);因此求解思路大致分为搜索求解,代数方法求解,问题变换求解三种基本思路,按照这样的划分,本文要介绍以下4种baseline算法:

• BCS算法(Boolean Characteristic Set Algorithm)[1]:基于经典代数消元方法吴消元法的求解算法;
• Groebner基算法[2]:基于多项式理想构造算法Groebner Basis的求解算法(基于SAGE V9.2的Polybori库实现);
• FESLib库(Fast Exhaustive Search Algorithm)[3]:基于分治+解空间搜索的求解算法(复杂度是指数级别);
• 转SAT算法(Boolean Equations to SAT Algorithm)[4]:将布尔方程组问题转化为等价的SAT问题再使用SAT求解器求解的算法(基于Cryptominisat实现);

在本文中,我们主要侧重实现(所有代码均在Linux下编译实现),理论部分可以详见参考文献(如有需要,我会另外写博客来分别介绍这4篇工作的技术细节部分);

BCS算法(Boolean Characteristic Set Algorithm)

BCS算法 [1] 虽然基于吴消元法计算特征列,但是巧妙利用了布尔多项式的加法特点,克服了原方法里多项式膨胀的问题:

在 中做拟除 Pesudo-division: 利用多项式 去消元 中的 . 计算:

其中均为多项式,因此这样的运算会导致快速的多项式阶和项数的膨胀(这样的膨胀每次消元都会发生);

本文防止消元的多项式膨胀的方法主要依赖以下两点:

• 零点分解,作情况分支:
  

• 上加法消元: .

更具体的算法可以参考原文,下面给出代码实现(源代码:https://github.com/hzy-cas/BCS);算法实现依赖CUDD包,该包主要实现了表示布尔函数的二元决策图数据结构 BDD(Binary Decision Diagram)及其相应算法,在选取初式时会更快;CUDD包的编译(使用cudd-2.4.2):

首先是修改Makefile里的XCFLAGS(对应主机的gcc版本):

XCFLAGS	= -mtune=native -DHAVE_IEEE_754 -DBSD -DSIZEOF_VOID_P=8 -DSIZEOF_LONG=8

尔后就是make,我没有make install,之后的依赖编译都是手动路径;下面是编译BCS算法的代码的Makefile(编译的cudd放在”/download/my_install/cudd-2.4.2″):

CFILES = main.cpp
INSTALL_DIR = /download/my_install/cudd-2.4.2
INCLUDING_PATH = /download/my_install/cudd-2.4.2/include
OBJFILES = main.o binary.o IO.o zddrcs.o zddrp.o zddrps.o zddrpss.o
CFLAGS = -pg
CFLAGS = -g -I$(INCLUDING_PATH) -L$(INSTALL_DIR)/cudd -L$(INSTALL_DIR)/epd -L$(INSTALL_DIR)/mtr -L$(INSTALL_DIR)/st -L$(INSTALL_DIR)/util
CC = g++
LIBS = -lcudd -lmtr -lst -lutil -lepd
DDDEBUG = -DDD_STATS

wu_char: main.o binary.o IO.o zddrcs.o zddrp.o zddrps.o zddrpss.o 
	$(CC) -o wu_char $(CFLAGS) $(OBJFILES) $(LIBS)

binary.o: binary.cpp 
	$(CC) -c $(CFLAGS) binary.cpp

IO.o: IO.cpp 
	$(CC) -c $(CFLAGS) IO.cpp

zddrcs.o: zddrcs.cpp 
	$(CC) -c $(CFLAGS) zddrcs.cpp

zddrp.o: zddrp.cpp 
	$(CC) -c $(CFLAGS) zddrp.cpp

zddrps.o: zddrps.cpp 
	$(CC) -c $(CFLAGS) zddrps.cpp

zddrpss.o: zddrpss.cpp 
	$(CC) -c $(CFLAGS) zddrpss.cpp

main.o: main.cpp 
	$(CC) -c $(CFLAGS) main.cpp

clean: 
	\rm -f $(OBJFILES)

用BCS算法求解一个变元数的二次型布尔方程组:

[hanss@Mint]$ ./wu_char
--------------BCS algorithm by Zhenyu Huang, Version 1.2----------------
Please choose the RUNNING MODE:
0 for PoSSo mode(obtian all solutions );
1 for SAT mode (obtain one monic triangular set);
2 for Counting mode (Counting zero number);
0
-----------------Solving Mode: Obtain all solutions-------------------
Please input the name of the file containing the input polynomial system:
n16m32.poly
... ...
x1+1,x2+1,x3,x4+1,x5,x6+1,x7,x8,x9+1,x10+1,x11,x12+1,x13,x14,x15,x16

其中”x1+1″代表,”x3″代表,以此类推;

Groebner基算法(PolyBori in SageMath V9.2)

定义(Groebner基): 多项式组 称为 Groebner 基, 如果范式 对所有 都是惟一的. 称 为多项式组 或理想 的 Groebner 基, 如果 是 Groebner 基, 且 .

每个理想都有一个由有限多个多项式构成的 Groebner 基. 这一点可以由 下面的 Hilbert 基定理保证(每个多项式理想 都是有限生成的). 后面我们将会看到, 一个理想的约化 Groebner 基 (附加一定条件的 Groebner 基) 在某种意义下是惟一的. 所以, 通常在提到理想的 Groebner 基时, 总认为它是有限的. 而 Groebner 基本质上也是具有良好性质(对约化/消元/理想成员判定有利)的理想;

利用 Groebner 基算法求解多项式方程组,本质上是在求原多项式方程组的消元理想;消元理想定义为:

它意味着已经从多项式方程组中被消去了,这个过程进行到单个变元时,方程就被求解了;

基于 SageMath V9.2 的 PolyBori 的实现,求解变元数的二次型布尔方程组(完整代码):

from sage.sat.converters.polybori import CNFEncoder
from sage.sat.solvers.dimacs import DIMACS

BOOLEAN_RING.<p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13,p14,p15,p16,p17,p18,p19,p20,p21,p22,p23,p24,p25,p26,p27,p28,p29,p30,p31,p32,p33,p34,p35,p36,p37,p38,p39,p40> = BooleanPolynomialRing()
ITEMS_BOOLEAN = [p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13,p14,p15,p16,p17,p18,p19,p20,p21,p22,p23,p24,p25,p26,p27,p28,p29,p30,p31,p32,p33,p34,p35,p36,p37,p38,p39,p40];

EQUATIONS_MQ = mq_coeff_2_poly(SAVED_PATH + "/mq_eqs_"+str(1)+".coeff",ITEMS_MQ + [1]);

IDEAL_MAIN = ideal(EQUATIONS_MQ);
GB_MAIN = IDEAL_MAIN.groebner_basis();
print_equations(GB_MAIN);

求解结果及含义和BCS算法一样:

GB_MAIN = [p1 + 1,p2,p3 + 1,p4,p5 + 1,p6,p7 + 1,p8,p9 + 1,p10 + 1,p11 + 1,p12,p13 + 1,p14,p15,p16];

转SAT算法(Boolean Equations to SAT Algorithm)

求解上二次多元方程(MQ问题)是NP-困难的,另一个NP-困难的问题是逻辑表达式可满足性问题(SAT问题).因为所有的NP-完全问题都是多项式可归约的,所以用SAT问题的有效求解工具(如SAT求解器)等可以求MQ问题的解.

例(布尔方程和命题逻辑表达式的转换):布尔方程 可以翻译成如下等价的一组命题逻辑合取范式表达式全部取真:

比如 true 和 true, 这就导致若欲使子句 (2) 为真, 须令 true 才能满足. 同理,若 false, true and true, 原布尔方程虽然满足但是子句 (1) 产生 conflict 为假.

因此将布尔方程(Algebraic Normal Form (ANF))转化为命题逻辑合取范式(CNF)再用 SAT 求解器求解属于转换求解;实现如下(完整代码):

from sage.sat.converters.polybori import CNFEncoder
from sage.sat.solvers.dimacs import DIMACS

# --- 变元声明 ---
BOOLEAN_RING.<p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13,p14,p15,p16,p17,p18,p19,p20,p21,p22,p23,p24,p25,p26,p27,p28,p29,p30,p31,p32,p33,p34,p35,p36,p37,p38,p39,p40> = BooleanPolynomialRing()
ITEMS_BOOLEAN = [p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13,p14,p15,p16,p17,p18,p19,p20,p21,p22,p23,p24,p25,p26,p27,p28,p29,p30,p31,p32,p33,p34,p35,p36,p37,p38,p39,p40];

# --- 读取布尔方程组 ---
EQUATIONS_MQ = mq_coeff_2_poly(SAVED_PATH + "/mq_eqs_"+str(1)+".coeff",ITEMS_MQ + [1]);

# --- ANF转换为CNF表达式并存储为.cnf文件 ---
TMP_FILE   = tmp_filename();
SAT_SOLVER = DIMACS(filename=TMP_FILE);
ANF2CNF_ENC = CNFEncoder(SAT_SOLVER, BOOLEAN_RING);
for POLYNOMIAL in EQUATIONS_MQ:
    ANF2CNF_ENC.clauses_dense(POLYNOMIAL);
WRITED_FILE = SAT_SOLVER.write();
WRITED_FILE = open("baseline_cryptominisat.cnf",'w');
print(open(TMP_FILE).read(),flush=True,file=WRITED_FILE);

# --- 调用 cryptominisat 求解 ---
os.system('cryptominisat5 --verb 0 baseline_cryptominisat.cnf');

求解一个问题的toy级别的布尔方程组,转SAT的过程中由于需要切割多项式,会以多项式级别的复杂度新增一些新变元,求解结果里,如”44″代表,”-41″代表,以此类推:

[hanss@Mint]$ /App/SageMath/SageMath/sage baseline_cryptominisat.sage
s SATISFIABLE
v 1 -2 3 4 5 -6 7 -8 -9 -10 -11 -12 -13 -14 -15 -16 -17 -18 -19 -20 -21 -22 -23 
v -24 -25 -26 -27 -28 -29 -30 -31 -32 -33 -34 -35 -36 -37 -38 -39 -40 -41 42 43 
v 44 45 -46 -47 -48 -49 -50 51 52 -53 54 55 56 -57 -58 59 -60 -61 -62 -63 64 
v -65 66 -67 68 -69 -70 -71 -72 -73 -74 -75 76 77 -78 -79 -80 81 82 -83 -84 -85 
v -86 -87 -88 -89 90 -91 -92 93 94 95 -96 97 98 -99 100 101 102 -103 104 -105 
v 106 -107 108 109 110 111 -112 113 114 -115 -116 -117 118 119 -120 -121 -122 
v 123 124 125 -126 127 -128 129 130 131 132 -133 -134 135 -136 -137 -138 -139 
v 140 141 -142 143 144 145 -146 147 148 149 -150 -151 152 153 0
[Finished in 4.0s]

基于解空间搜索的FESLib库(Fast Exhaustive Search Algorithm)

这篇工作首先定义了 上的求导概念(这可以在解迭代过程中有效减少位操作次数加速搜索):

定义(Derivatives on ): 令 上对应第 个变元的求导 为 . 那么对于任意解向量 , 有:

其中即为第位为1的解向量(one-hot 向量);那么解空间搜索的初始化操作INIT()和迭代操作NEXT()可以形式化为:

cmake_minimum_required(VERSION 3.10)

project(feslite VERSION 1.0 
	LANGUAGES C ASM)

include(CTest)

if(NOT CMAKE_BUILD_TYPE AND NOT CMAKE_CONFIGURATION_TYPES)
  message(STATUS "Setting build type to 'Debug' as none was specified.")
  set(CMAKE_BUILD_TYPE "Debug" CACHE STRING "Choose the type of build." FORCE)
endif()

add_compile_options(-Wall -Werror -O3 -Wno-unused-function)

set(CMAKE_C_STANDARD 99)
set(CMAKE_C_STANDARD_REQUIRED True)

find_package(OpenMP)

if (DEFINED ENV{NO_SSE})
    message(STATUS "As per $NO_SSE, disabling all simd intrinsics")
else()
    include("config/sse2.cmake")
    include("config/avx2.cmake")
    include("config/avx512.cmake")
endif()
if (DEFINED ENV{NO_NEON})
    message(STATUS "As per $NO_NEON, disabling all ARM NEON intrinsics")
else()
    include("config/neon.cmake")
endif()

configure_file(src/feslite-config.h.in src/feslite-config.h)

add_subdirectory(src)
add_subdirectory(benchmark)

if(BUILD_TESTING)
  add_subdirectory(test)
endif()

make的过程中有对源代码中含”#pragma GCC unroll 64″这句指令的文件报错,这是一句加速循环的指令,可能和主机系统有关,只能注销掉:

[hanss@Mint]$ sed "s/#pragma GCC unroll 64/\/\/#pragma GCC unroll 64/g" -i ./src/*.c

然后再make即可,我们重点展示一下怎么使用它解一个变元数的布尔方程组(关键部分我做了注释,生成方程组.dat文件的代码和计算代码见完整代码):

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "feslite.h"
#include "cycleclock.h"

int main()
{
    int n = 32; // num of variables;
    int k = 32; // num of quadratic boolean equations;
    int m = 16;

    /* Reading Numbers from File */
    u32 Fq[496]; // Quadratic terms num = C(2,32); Think about why not 496*m?? The fact is that any two systems in m systems have the same quadratic terms(which can be veritified by computing examples);
    u32 Fl[33 * m]; // Linear terms num = num of variables + 1;
    // === Reading The Equations from file fq_and_fl_array.dat ===
    FILE *FILE_IO_COUNT,*FILE_IO_READ;char TMP_CHAR;char NUM_CHAR[20];char READ_CHAR[20];int TMP_NUM;
    FILE_IO_COUNT = fopen("fq_and_fl_array.dat","r");FILE_IO_READ = fopen("fq_and_fl_array.dat","r");
    for (int INDEX_i = 0; INDEX_i < 496; ++INDEX_i)
    {
        int COUNT_BIT = 0;TMP_CHAR = fgetc(FILE_IO_COUNT);
        while(TMP_CHAR != ','){COUNT_BIT++;TMP_CHAR = fgetc(FILE_IO_COUNT);}
        fgets(NUM_CHAR, COUNT_BIT+1, FILE_IO_READ);
        fgets(READ_CHAR, 2, FILE_IO_READ);
        Fq[INDEX_i] = char2u32(NUM_CHAR);
    }
    for (int INDEX_i = 0; INDEX_i < 33*m; ++INDEX_i)
    {
        int COUNT_BIT = 0;TMP_CHAR = fgetc(FILE_IO_COUNT);
        while(TMP_CHAR != ','){COUNT_BIT++;TMP_CHAR = fgetc(FILE_IO_COUNT);}
        fgets(NUM_CHAR, COUNT_BIT+1, FILE_IO_READ);
        fgets(READ_CHAR, 2, FILE_IO_READ);
        Fl[INDEX_i] = char2u32(NUM_CHAR);
    }
    // === Reading End ===

    /* solve */
    u32 solutions[256 * m]; // Stored solutions;
    int size[m]; // Record how many solutions can be found of each system;
    uint64_t start = Now(); // Record the start time;
    feslite_solve(n, m, Fq, Fl, 256, solutions, size); // Solving m systems once;
    uint64_t stop = Now(); // Record the stop time;

    /* report */
    int kernel = feslite_default_kernel(); // Solver kernel;
    const char *name = feslite_kernel_name(kernel); // Which kernel used;
    printf("%s : %d lanes, %.2f cycles/candidate\n", 
        name, m, ((double) (stop - start)) / m / (1ll << n)); // Print time cost;
    for (int i = 0; i < m; i++)
    printf("Lane %d : %d solutions found\n", i, size[i]); // Print solving results;
    return EXIT_SUCCESS; // Ending;
}

这里我在看源代码时一直有个疑惑,这不是在求解 上的方程组吗,为什么系数数组 Fq[] 和 Fl[] 的类型是无符号32位整数 u32 ??于是我发邮件询问了作者,作者回复:

Here is an explanation:
Fl[0] contains the constant term
Fl[i + 1] contains the coefficient of the linear monomial x_i (variables are x_0, …, x_{n-1}).
Fq[idxq(i,j)] contains the coefficient of the quadratic monomial x_i*x_j, with i < j. The function idxq() is defined in fes.h
Now, all these coefficients are indeed 0/1. The trick is that there are 32 equations, and that the code uses “bitslicing”. It uses a single array of 32-bit words to represent the 32 equations. The j-th bit of Fl[0] contains the constant term of the j-th equation ; the j-th bit of Fl[i+1] contains the coefficient of x_i in the j-th equation, etc.
So, the statement :
Fq[i] = lrand48() & ((1ll << k) - 1);
Initializes randomly the coefficient of a quadratic monomoial in k simultaneous equations.

妙啊,也就是说它作了位切割,一个u32整数实际上代表的是整个方程组里确定项序下同一个项的所有系数,这里我自己画了图来说明:

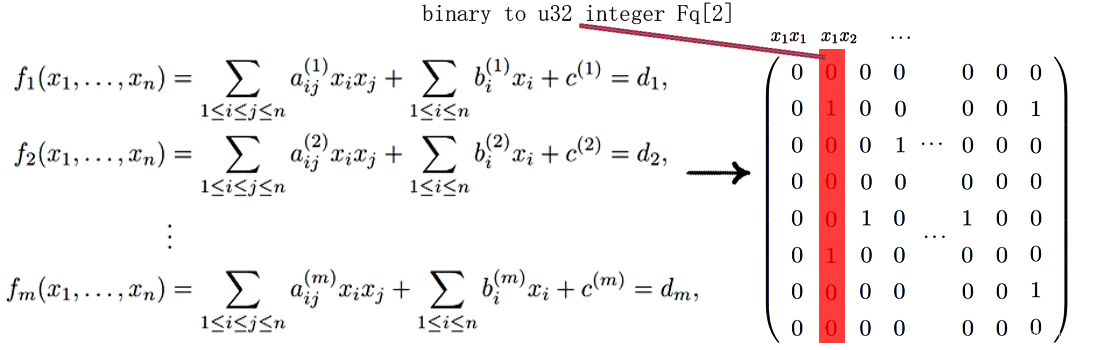
feslite_solve(n, m, Fq, Fl, 256, solutions, size);

后来发现论文使用了一个简单的分治策略,比如在求解的方程组时,遍历的解,则可以把原方程分支为个规模的方程组,这也是接口函数里 m 的含义(分支和写入.dat文件的sage代码见完整代码);那么编译运行:

[hanss@Mint]$ gcc solver_n40.c -o exe -I/download/my_install/libfes-lite-10years/src -L/download/my_install/libfes-lite-10years/build/src -lfeslite
[hanss@Mint]$ ./exe
avx2_16x16 : 16 lanes, 0.06 cycles/candidate
Lane 0 : 0 solutions found
... ...
Lane 15 : 1 solutions found

参考文献

[1] Zhenyu Huang, Yao Sun, Dongdai Lin, On the efficiency of Solving Boolean Polynomial Systems with the Characteristic Set Methods, Journal of Symbolic Computation, 2019.
[2] Michael Brickenstein and Alexander Dreyer, PolyBoRi: A framework for Gröbner-basis computations with Boolean polynomials, Journal of Symbolic Computation, 2009;
[3] Bouillaguet, Charles and Chen, Hsieh Chung and Cheng, Chen Mou and Chou, Tung and Yang, Bo Yin, Fast Exhaustive Search for Polynomial Systems in F2, Cryptographic Hardware and Embedded Systems, CHES 2010, 12th International Workshop, Santa Barbara, CA, USA, August 17-20, 2010.
[4] Soos M., Nohl K., Castelluccia C.: Extending SAT Solvers to Cryptographic Problems. In: Kullmann O.(eds) Theory and Applications of Satisfiability Testing – SAT 2009. SAT 2009. Lecture Notes in Computer Science, vol 5584. Springer, Berlin, Heidelberg, 2009.