从开放集分类的角度重新思考基于Softmax的人脸识别
GB-CosFace: Rethinking Softmax-based Face Recognition from the Perspective
of Open Set Classification
1摘要:
- 背景:目前最先进的人脸识别方法通常采用多分类管道,并采用基于softmax的损失进行优化。
- 问题:尽管这些方法取得了巨大的成功,但从开放集分类的角度来看,基于softmax的损失有其局限性:训练阶段的多分类目标与开放集分类测试的目标并不严格匹配。
- 提出方案:在本文中,我们得出了一个新的损失,名为全局边界CosFace(GB-CosFace)。我们的GB-CosFace引入了一个自适应的全局边界来确定两个人脸样本是否属于同一身份,这样,从开放集分类的角度来看,优化目标与测试过程是一致的。同时,由于损失公式来自于基于softmax的损失,我们的GB-CosFace保留了基于softmax的损失的优良特性,而且CosFace被证明是所提出的损失的一个特例。我们从几何学的角度分析和解释了所提出的GB-CosFace。在
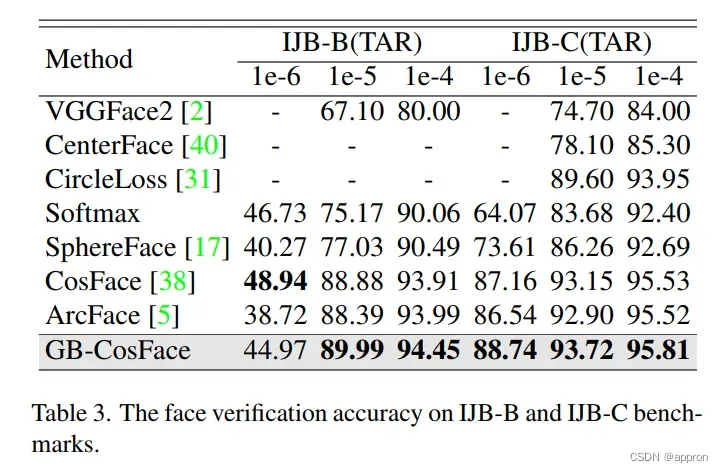
- 效果:多个人脸识别基准上的综合实验表明,所提出的GB-CosFace在主流人脸识别任务中优于目前先进的人脸识别损失。与CosFace相比,我们的GB-CosFace在TAR@FAR=1e-6、1e-5、1e-4的IJB-C基准上提高了1.58%、0.57%和0.28%。
2引言:
对人脸识别(FR)的训练目标的研究有效地提高了基于深度学习的人脸识别的性能[32, 34, 39, 40]。根据是用代理来代表一个人的身份还是一组训练样本,人脸识别方法可以分为无代理方法[4, 8, 12, 22-24, 27, 29, 30,35,42,48]和基于代理的方法[3,5,15,17,20,31, 33, 36-38, 47]。
- 无代理的方法直接压缩类内距离,并基于成对学习[4, 12, 30, 35]或三联学习[8, 22, 23, 27, 29, 42, 48]扩大类间距离。然而,当处理大量的训练数据时,对无代理方法至关重要的硬挖掘操作变得非常困难。
- 最近,基于代理的方法取得了巨大的成功,并在大数据训练中显示出优势。它们中的大多数采用了基于softmax的多分类管道,并使用交叉熵损失作为优化目标。在这些方法中,训练集中的每个身份都由一个原型来代表,这个原型是最终全连接层的权重向量。
在本文中,我们将这类方法称为基于软键的人脸识别方法。
传统的为近似集多分类问题设计的softmax-cross-entropy loss并不适合人脸识别这样的开放集分类问题。目前基于softmax的人脸识别方法已经对训练目标进行了各种改进。其中最关键的改进是将人脸特征归一到超球上,以便进行统一的比较[17, 37]。通常情况下,两个样本之间的相似性由其相应的特征向量的余弦相似性来表示。给定训练样本的特征向量和训练身份的原型,训练目标是压缩特征向量与相应原型之间的距离,并将其他原型从特征向量中推开。为了进一步压缩类内距离和扩大类间距离,人们提出了基于大边际的方法[5,17,36,38]。最近,对尺度参数[44]和边际参数[16,20]的动态方案进行了研究,进一步提高了模型性能。

尽管基于softmax的人脸识别取得了巨大的成功,但从开放集分类的角度来看,这种策略有其局限性[9, 10, 26, 43]。如图1(a)所示,基于softmax的多分类法的训练目标是使目标类别的预测概率大于其他类别。然而,人脸识别是一个开放集分类问题,测试类别一般不存在于训练类别中[39]。对人脸识别模型的一个典型要求是通过比较两个样本与全局阈值T的相似度来确定它们是否属于同一身份,如图1(b)所示。(即人脸比对)训练和测试目标的不一致限制了性能。基于这种考虑,我们认为在训练和测试期间目标的一致性需要在损失设计中加以考虑。
在本文中,我们提出了一种新的人脸识别损失,名为全局边界CosFace(GB-CosFace)。在我们的GB-CosFace框架中,通过引入由拟议的自适应边界策略确定的全局边界,训练目标与测试过程保持一致。
- 首先,我们比较了基于softmax的损失和人脸识别测试过程之间的目标差异。
- 然后,我们从开放集分类的角度抽象出合理的训练目标,并推导出拟议损失的反类型。
- 此外,我们将基于softmax的损失的优秀特性与提议的antetype损失相结合,得出最终的GB-CosFace表述,并证明CosFace[36,38]是提议的GB-CosFace的一个特殊情况。
- 最后,我们对提出的GB-CosFace进行了几何学上的分析和解释。
本文的贡献总结如下。
- – 我们提出了用于人脸识别的GB-CosFace损失,它符合开放集分类问题测试过程的目标,同时继承了基于softmax损失的优点。
- – 我们分析了GB-CosFace与一般基于softmax的损失之间的区别和联系,并给出了合理的几何解释。
- – 我们的GB-CosFace明显改善了基于softmax的人脸识别的性能(例如,与CosFace相比,在TAR@FAR=1e-6、1e-5、1e-4的IJB-C基准上提高了1.58%、0.57%和0.28%)。
3.基于softmax的人脸识别
为了更好地理解所提出的GB-CosFace,本节回顾了基于softmax的一般人脸识别方法。
3.1框架
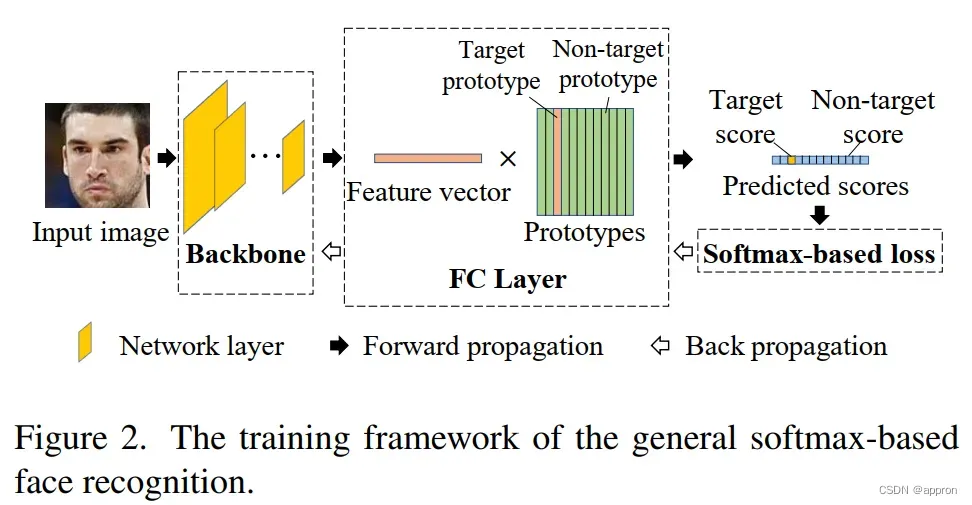
基于softmax的人脸识别的训练框架如图2所示。在这个框架中,训练集中的每个身份都有其相应的原型。原型由最后的全连接层的权重向量表示。给定一个训练样本,我们把代表该样本身份的原型称为 “目标原型”,而把其他原型称为 “非目标原型”。在骨干的面部特征提取之后,通过最后的全连接层(FC层)计算代表特征向量和每个原型之间相似性的预测分数。特征向量与目标原型之间的相似度被称为 “目标分数”,其他预测分数被称为 “非目标分数”。一般来说,输出特征向量和原型被归一化为单位超球。因此,预测分数通常由特征向量和原型的余弦表示。在训练中,通过反向传播,采用基于softmax的损失来优化骨干层和最终的FC层。
3.2目标
对于n类人脸识别训练中的每一次迭代,给定一个训练样本和它的标签y,一般基于softmax的损失如下。
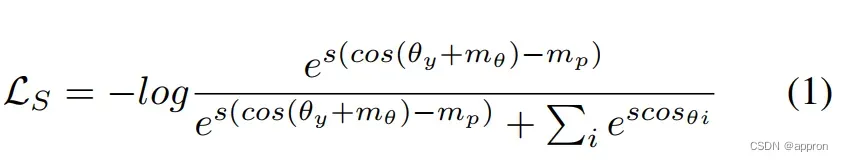
其中,θ y是预测特征向量与目标原型之间的弧线,θi是预测特征向量与非目标原型之间的弧线,y是目标身份的索引,i是非目标身份的索引,i 2 [1; n],i 6= y。有三个超参数:尺度参数 “s”,以及两个边际参数 “mθ “和 “m p”。
我们可以从等式中得出几个常见的基于softmax的损失。1.例如,如果mθ和mp都设置为0,就可以达到归一化的softmax损失。如果我们分别将mp和mθ设置为0,就可以达到ArcFace和CosFace。 基于软性最大的损失可以被视为以下优化目标OS的平滑形式。
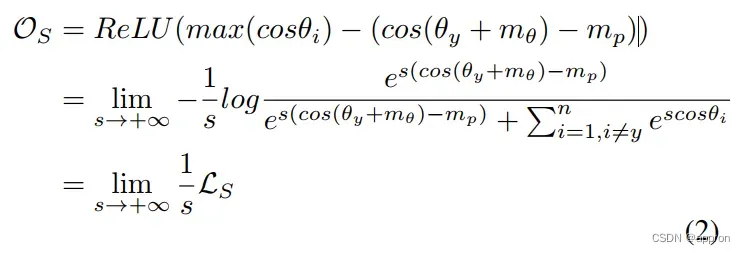
从这个角度来看,我们可以发现,训练目标OS约束目标分数要大于最大的非目标分数。引入保证金是为了更严格的约束。然而,这种约束与测试过程的目标并不完全一致。 基于公式2,我们可以直观地看到决策边界。2,我们可以直观地看到二元分类情况下的归一化softmax loss[37]、CosFace[36,38]和ArcFace[5]的决策边界,如图3(a)-(c)所示。在测试阶段,需要固定余弦相似度的全局阈值T来判断两个样本是否属于同一个人,如图3(d)所示。我们可以看到,即使增加了一个保证金,基于softmax的损失的决策边界也不完全符合测试的预期边界。
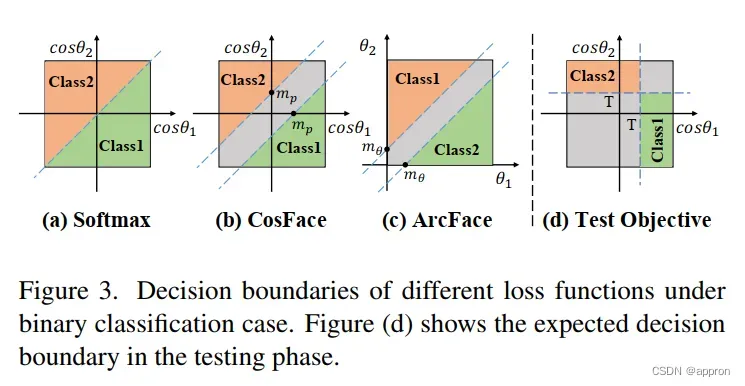
注:训练目标针对的是各个margin,即cosθ1-cosθ2>margin,测试时目标是maxθ>T,只关注最大类,而不关注与其他类的关系.
属性:
目前的人脸识别模型并没有直接应用OS作为训练目标。一方面,max(-)运算符只关注最大值,梯度将只反向传播到目标分数和最大非目标分数。另一方面,如果RELU函数的参数小于0,则没有梯度被反向传播。作为OS的一种平滑形式,基于softmax的损失可以避免上述问题。基于softmax的损失的成功是由于其出色的特性。
属性1. 非目标分数的梯度与它们的softmax值成正比。对于基于softmax的损失,反向传播的梯度将根据其softmax值分配给所有非目标分数。这一属性保证了每个非目标原型都能在训练中发挥作用,而硬的非目标原型会得到更多的关注。
属性2. 目标分数的梯度和所有非目标分数的梯度之和具有相同的绝对值和相反的符号。
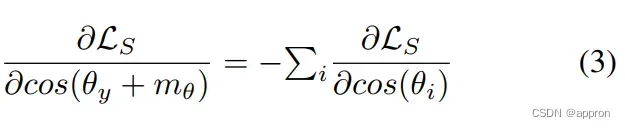
基于Softmax的损失对目标分数和非目标分数具有平衡的梯度。考虑到这两个特性在人脸识别训练中的关键作用,我们希望在损失设计中继承它们。在本文中,我们通过引入一个自适应的全局边界,将训练和测试的一致性加入到损失设计中。从预期的训练目标出发,我们推导出我们的GB-CosFace框架,并证明与CosFace的兼容性。这种兼容性使得所提出的损失继承了一般基于softmax的损失的优良特性,同时解决了训练和测试目标之间的不一致性。
4.GB-CosFace框架
4.1Antetype Formulation
基于图3(d)所示的人脸识别测试过程,我们建议引入一个全局阈值pv作为目标分数和非目标分数的边界。目标分数需要大于pv,而非目标分数的最大值则需要小于pv。2如下。
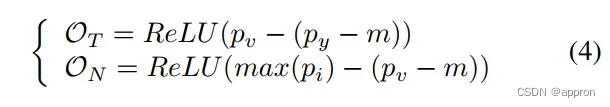
其中,我们将训练目标分为目标分数和非目标分数的OT和ON,py是目标分数,py=cosθy,pi是非目标分数,pi=cosθi,m是为了更严格的约束而引入的保证金参数。训练目标是使OT和ON最小化。 受基于softmax的损失的成功启发,与公式2相似,我们采用平滑的形式。2,我们将OT和ON的平滑形式作为拟议损失的反类型。
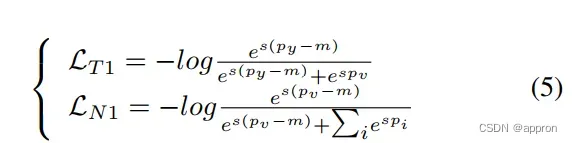
其中,目标分数和非目标分数的损失分别表示为LT 1和LN1,pv是全局边界超参数,也意味着 “虚拟分数”。对于LT 1,pv是一个虚拟的非目标分数。 对于LN1,pv是一个虚拟的目标分数。由于我们把log P exp(-)作为max(-)的平滑形式,非目标分数的梯度分布继承了基于softmax的损失的属性1.(在第2.3节陈述)。
首先,不恰当的pv设置会导致严重的梯度不平衡问题。由于我们将目标分数和非目标分数的约束分开,目标分数和非目标分数的梯度平衡被打破,反类型损失不再保留属性2。第二,考虑到指数函数的快速上升和超参数 “s “的放大效应,该模型对超参数pv的选择极为敏感,如图4所示,pv的轻微变化就会导致目标分数py和非目标分数pi的梯度之间出现数量级的差异。第三,考虑到每个样本的预测分数在训练过程中是动态的,理想的阈值pv也应该是一个动态参数以适应不同的训练阶段。因此,一个全局边界的自适应方案是必要的
4.2自适应决策边界
为了控制梯度平衡,使全局边界适应不同的训练阶段,我们提出了一种自适应全局边界方法。我们认为一个理想的全局边界应该满足以下条件:a)在这个边界设置下,从全局角度看,目标分数和非目标分数的梯度应该是大致平衡的;b)全局边界在训练过程中应该缓慢变化,以保持训练的稳定性,同时适应不同的训练阶段。基于这两个条件,我们做了如下设计。
梯度平衡控制
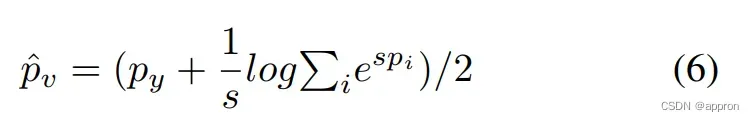
每个样本的平均pv
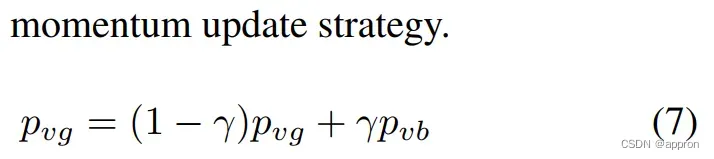 移动平均pvg:上一个阶段的pvg 和本批次pvb的加权平均
移动平均pvg:上一个阶段的pvg 和本批次pvb的加权平均
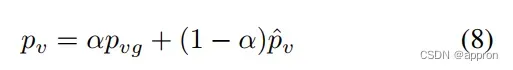
移动平均pv:本阶段的pvg和本样本pv的加权平均.
最终的损失
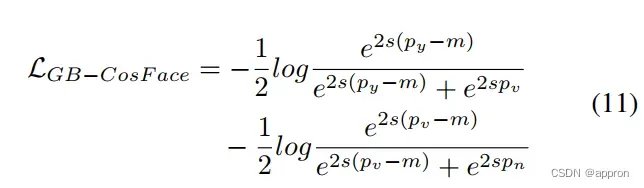
核心是单独优化每个目标到边界。
实验结果
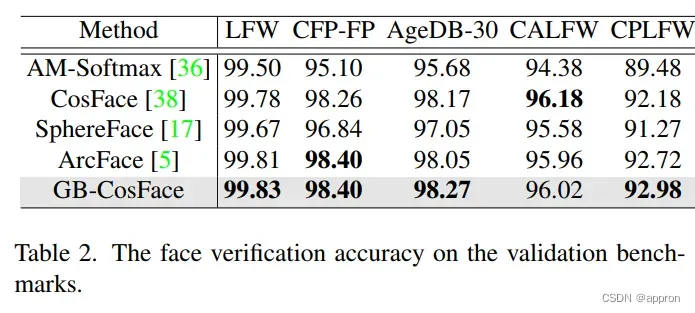
文章出处登录后可见!
