最近认真阅读了一份商业分析的咨询报告案例,并分析了其写作思路,有兴趣请戳:商业分析、咨询报告思路详细解读(CASE R001) – 知乎
在仔细分析完这份报告中,发现商业领域中的咨询报告都逃不过“市场规模预测”的部分,而市场规模预测通常又与统计学中时间序列预测的内容脱离不了干系。所以,来恶补一下时间序列分析的内容,并探究如何在R中实现时间序列的预测。本内容来源于Rob J Hyndman 和 George Athanasopoulos的《Forecasting:principles and practice》。这本书是免费的,电子书资源网站:预测: 方法与实践
本文是时间序列预测在R中的应用的第一部分,涉及到目录中1 Introduction以及2 预测的工具及部分。
目录
1 Introduction
每个环境都是在变化的,并且一个优秀的预测模型会捕捉事物变化的方式。根据时间跨度、确定实际结果的因素、数据模式的类型以及许多其他方面,预测情况会有很大的不同。预测方法可以非常简单,例如使用最近一次观测作为预测(被称为“朴素方法”),也可以很复杂,例如神经网络和联立方程的计量经济系统。
1)进行预测的步骤
- 定义问题。此步骤需要了解怎样运用预测方法,谁需要这个预测,以及预测效果如何满足需要这个预测的机构。
- 收集信息。一般会收集统计数据和专家经验建议。
- 初步(探索性)分析。通常会使用数据可视化的方式来对数据结构进行初步探索。我们通过可视化可以发现有明显的长期趋势吗?季节性重要吗?是否有证据表明商业周期存在?数据中是否包含需要专业知识解释的异常值?用于分析的变量之间的相关性有多强?
- 选择及拟合模型。目前已有多种模型供我们选择,我们可以根据探索性分析中对数据结构的把握,来选择合适的模型进行时间序列预测。如回归模型、指数平滑方法、Box-Jenkins ARIMA模型、动态回归模型、分层预测,以及其他各种方法,包括计数时间序列、神经网络的向量自回归。
- 使用及评估预测模型。模型的预测效果只有用于预测的数据得到之后才能得到正确的评价。
可以看出,与一般数据建模的思路相同:建模过程都要从所需解决的问题入手,再到收集数据、探索性分析、选择拟合模型、模型评估调整的步骤。
2)预测数据和方法
数据决定了选择什么样的模型进行预测。大多数定量预测问题都使用时间序列数据 (按时间间隔定期收集) 或横截面数据 (在一个时间点收集)。我们在日常生活中,主要专注于时间序列的领域:
时间序列数据:
任何按照时间顺序观察的事物都是时间序列。在预测时间序列数据时, 目的是估计观测序列将如何持续到未来。
最简单的时间序列预测方法只用了预测变量的信息,而不去寻找影响预测变量的因素。因此,这些方法可以推断趋势部分和季节性部分,但是它们会忽略掉所有其他的信息。关于时间序列的预测模型,可能有如下三种类型:
①解释模型:我们可以考虑一些其他有关外部变量的信息,而不仅仅是要预测的变量的。这类包含其他变量的模型可以称之为“解释模型”,例如:
ED=f(当前气温,经济实力,人口当日时间,星期几,误差)
②时间序列模型:对未来的预测是基于变量的历史值,而不是基于可能影响系统的外部变量。
EDt+1=f(EDt,EDt−1,EDt−2,EDt−3,…,误差)
t表示当前的时间,t+1表示下一个小时,t−1表示前一个小时,t−2表示前两个小时,以此类推
③混合模型:结合了上述两种模型的特点。例如, 它可能有如下形式:
EDt+1=f(EDt,当前气温,当日时间,星期几,误差)
虽然解释模型看起来非常有用,但是在实际运用中,预测者通常会选择使用时间序列模型:不仅仅因为其他模型太过复杂、难以理解和衡量、缺少和实践中管理行为的练习,最为关键的一点事,时间序列模型可以提供比解释或混合模型更准确的预测。在预测中使用的模型取决于可用的资源和数据、模型的准确性以及预测模型的使用方式。
3)统计预测观点
在大多数预测情况下,随着事件的临近,预测对象的相关变动较小。换句话说,预测的越早,预测结果越不稳定。
我们进行预测的过程实际是寻找随机变量可能取值范围内的中间值。通常情况下,预测会伴随着一个预测区间,给出一个随机变量具有较高概率的范围值。例如,95%的预测区间包含一系列的值,这个预测区间包含实际未来值的概率为95%。
2 时间序列基本可视化操作和工具集
1)时间序列图形
①ts对象:时间序列是一组按照时间发生先后顺序进行排列,并且包含一些信息的数据点序列。在R中,这些信息可以被储存在ts对象中。在下列代码中,z为已经储存的月度数据。
y <- ts(z, start=2003, frequency=12)②时间图:是进行时间序列分析最基本的图形。可以帮助我们判断数据的趋势和季节性因素。时间图是用将观测值与观测时间点作图,散点之间用直线连接。
library(fpp2)
autoplot(melsyd[,"Economy.Class"]) +
ggtitle("墨尔本 - 悉尼经济舱乘客客流量") +
xlab("年份") +
ylab("千")+
theme(text = element_text(family = "STHeiti"))+
theme(plot.title = element_text(hjust = 0.5))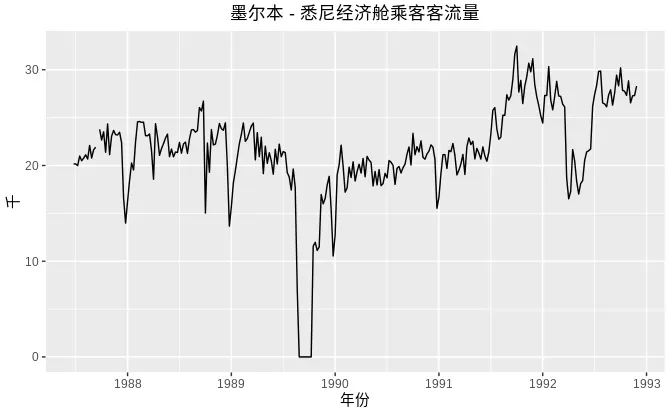
例如,在如上的时间图中,我们可以明显的发现乘客客流量随时间变化的波动,在描述时间序列时,我们通常使用如下词语:
- 趋势:当一个时间序列数据长期增长或者长期下降时,表示该序列有 趋势 。
- 季节性:当时间序列中的数据受到季节性因素(例如一年的时间或者一周的时间)的影响时,表示该序列具有 季节性。季节性总是一个已知并且固定的频率。
- 周期性:当时间序列数据存在不固定频率的上升和下降时,表示该序列有 周期性 。
③季节图:针对观察数据的“季节性”绘制的。
ggseasonplot(a10, year.labels=TRUE, year.labels.left=TRUE) +
xlab("月份")+
ylab("百万(美元)") +
ggtitle("季节图:降糖药物销量")+
theme(text = element_text(family = "STHeiti"))+
theme(plot.title = element_text(hjust = 0.5))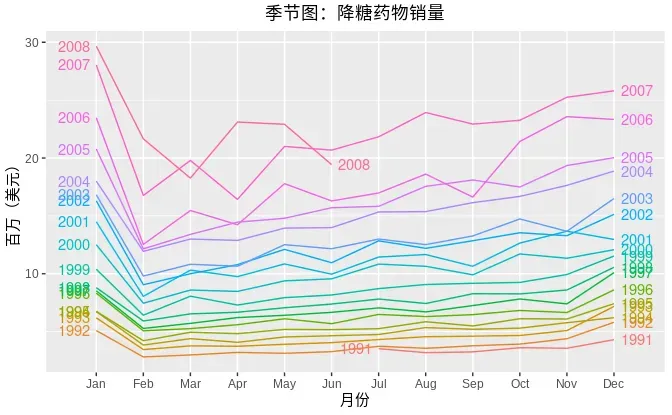
同时,我们可以通过ggsubseriesplot()函数着重描绘在相同月份数据的同比变化情况 。子系列季节图可以清晰的描绘出数据的潜在季节性形态,并且显示了季节性随时间的变化情况。这类图可以很好地查看各时期内数据的变化情况。
ggsubseriesplot(a10) +
xlab("月份")+
ylab("百万(每月)") +
ggtitle("子序列季节图:降糖药物销量")+
theme(text = element_text(family = "STHeiti"))+
theme(plot.title = element_text(hjust = 0.5))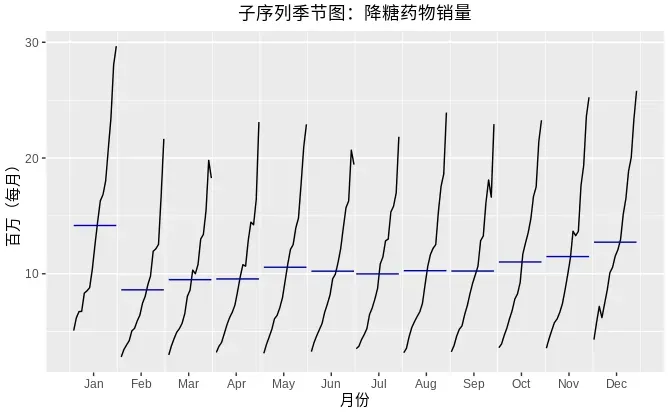
③散点图:多个时间序列的可视化。例如,我们可以在一张图上绘制两个时间序列的散点图来研究用电量和温度之间的关系。
qplot(Temperature, Demand, data=as.data.frame(elecdemand)) +
ylab("用电量 (千兆瓦)") + xlab("温度 (摄氏度)")+
theme(text = element_text(family = "STHeiti"))+
theme(plot.title = element_text(hjust = 0.5))不同变量间的关系可以使用相关系数r来衡量:
r的值始终在-1到1之间。当两个变量完全负相关时,r值为-1;当两个变量完全正相关时,r为1
④滞后图:滞后图的横轴表示时间序列的滞后阶数。通过观察滞后阶数是否具有正相关关系,可以用来说明数据是否具有很强的季节性。
⑤自相关:正如相关系数可以衡量两个变量之间的线性相关关系一样,自相关系数可以测量时间序列 滞后值 之间的线性关系。通过绘制自相关系数图可以描绘 自相关函数 或者是ACF。如果T是时间序列的长度,k为滞后值,当k=1时,可以使用r1衡量 yt和 yt−1 之间的关系;当k=2时,r2衡量 yt和yt−2 之间的关系,以此类推。
自相关系数图示例
ggAcf(beer2) +
ggtitle('') 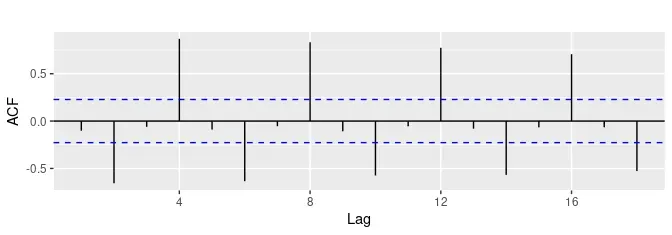
⑥白噪声 :“白噪声”是一个对所有时间其自相关系数为零的随机过程。如果一个序列中有较多的自相关值处于边界之外,那么该序列很可能不是白噪声序列,如果基本都在边界值之内,那么该序列很有可能属于白噪声序列。白噪声序列的特点表现在任何两个时点的随机变量都不相关,序列中没有任何可以利用的动态规律。
set.seed(30)
y <- ts(rnorm(50))
autoplot(y) + ggtitle("白噪声") +
theme(text = element_text(family = "STHeiti"))+
theme(plot.title = element_text(hjust = 0.5))2)预测者的工具集
有时候这些最简单的方法可能会是最好的预测方法,但是在很多情况下,这些方法只是作为基准方法而不是被直接运用。也就是说,我们提出的任何预测方法都会和这些简单方法比较,以保证其预测结果优于这些简单方法,否则,新的方法就不值得考虑。
①均值法:此方法中,所有未来值的预测值等于历史数据的平均值。
meanf(y, h)
# y 历史数据时间序列
# h 预测期数②Naïve 方法:在 naïve 预测方法中,我们简单地将所有预测值设为最后一次的观测值。
naive(y, h)
rwf(y, h) # 二者等价③季节性 Naïve 方法:我们将每个预测值设为同一季节的前一期观测值(例如:去年的同一个月)。
snaive(y, h)④漂移法:相对于 Naïve 方法,趋势法(漂移法)允许预测值随着时间的推移增大或减小,并且我们假定单位时间改变量(称作 “漂移”)等于历史数据的平均改变量,这相当于把第一个观测点和最后一个观测点连成一条直线并延伸到未来预测点。
rwf(y, h, drift=TRUE)本小结在R语言中的练习:
本部分是针对以上内容的训练,可以巩固本节所学到的内容
#2 时间序列图形练习
#设置环境\加载所需要的包
getwd()
setwd('D:/Code material/R/Time series')
getwd()
install.packages('ggfortify' )
install.packages('fpp2')
install.packages('readxl')
library('ggplot2')
library('ggfortify')
library('readxl')
library('forecast')
#读取文件、观察数据结构
tute1 <- read.csv("tute1.csv", header=TRUE)
View(tute1)
#将数据转化为时间序列格式
mytimeseries <- ts(tute1[,-1], start=1981, frequency=4)#使用[,-1]可以移除第一列的数据
autoplot(mytimeseries)
retaildata <- read_excel("retail.xlsx", skip=1)#package name::functionname的用法,一是可以在需要用某个函数时临时直接加载包,不用事先library。另一点更重要的是尽可能减少library带来的附带作用,这一点在开发R包时影响较大。
?read_excel
myts<-ts(retaildata[,"A3349873A"],frequency = 12,start = c(1982,4))
autoplot(myts)#时间图
ggseasonplot(myts)#季节图
ggsubseriesplot(myts)#子系列季节图
gglagplot(myts)#滞后图
ggAcf(myts)
#画出以下时间序列的格式
??bicoal
??chicken
??goog
autoplot(fma::bicoal)
autoplot(fma::chicken)
autoplot(fma::dole)#观察季节特征绘图练习
#writing
ggseasonplot(fma::writing)#8月会有剧烈下降
ggsubseriesplot(fma::writing)
#fancy
ggseasonplot(fma::fancy)#每年10月前平缓上升,第四季度开始显著攀升
ggsubseriesplot(fma::fancy)
#a10
??a10
ggseasonplot(fpp2::a10)#每年2月有较大幅度下降,后续月份缓慢攀升
ggsubseriesplot(fpp2::a10)
#hsales
??hsales
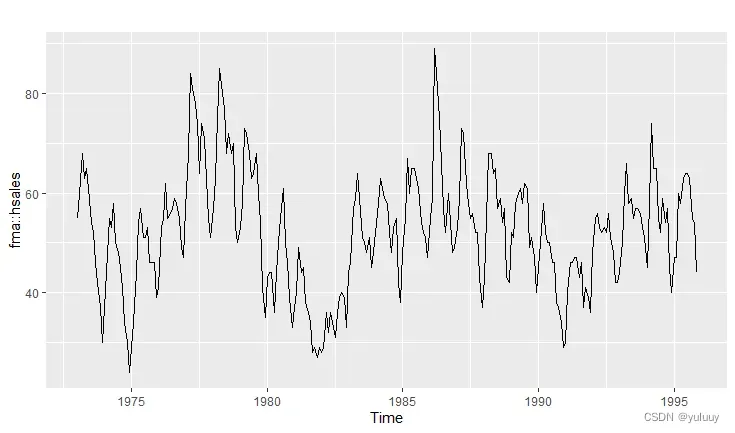
autoplot(fma::hsales)
ggseasonplot(fma::hsales)
ggsubseriesplot(fma::hsales)
gglagplot(fma::hsales)
ggAcf(fma::hsales)下面是以hsales为例,生成的时间序列图如下:
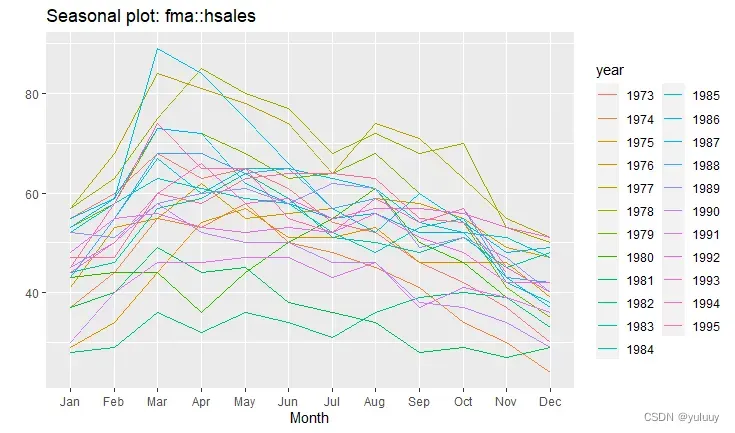
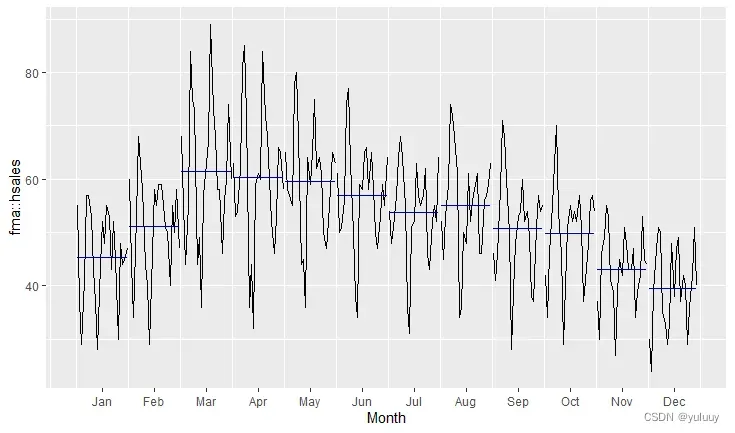
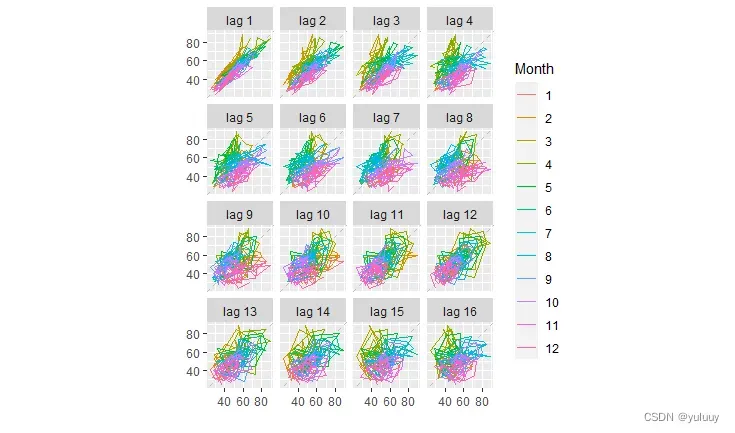
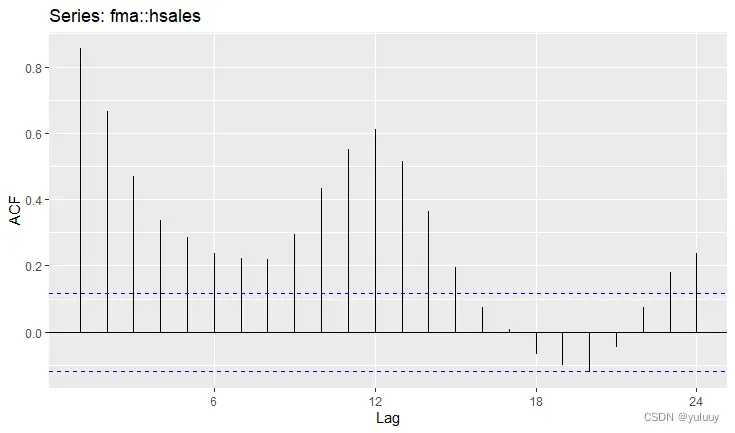
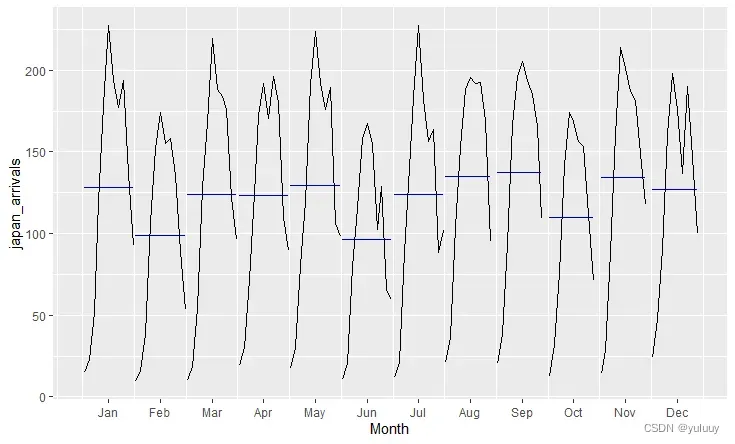
#arrivals数据包括从日本、新西兰、英国和美国到达澳大利亚的人数(千),比较不同国家到达澳大利亚人数的异同
??arrivals
View(fpp2::arrivals)
japan_arrivals<-ts(fpp2::arrivals[,"Japan"],frequency = 12)
NZ_arrivals<-ts(fpp2::arrivals[,"NZ"],frequency = 12)
UK_arrivals<-ts(fpp2::arrivals[,"UK"],frequency = 12)
US_arrivals<-ts(fpp2::arrivals[,"US"],frequency = 12)
#Japan
autoplot(japan_arrivals)
ggseasonplot(japan_arrivals)
ggsubseriesplot(japan_arrivals)
#NZ
autoplot(NZ_arrivals)
ggseasonplot(NZ_arrivals)
ggsubseriesplot(NZ_arrivals)
#UK
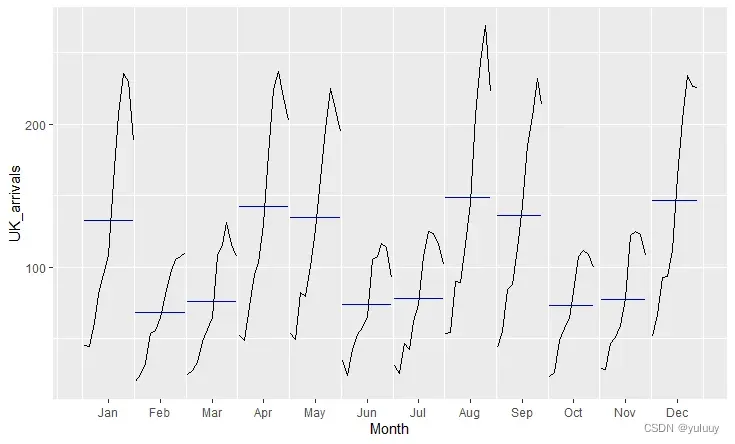
autoplot(UK_arrivals)
ggseasonplot(UK_arrivals)
ggsubseriesplot(UK_arrivals)
#US
autoplot(US_arrivals)
ggseasonplot(US_arrivals)
ggsubseriesplot(US_arrivals)
由于篇幅限制,这里只放出子系列季节图,来比对不同国家的客流量异同:
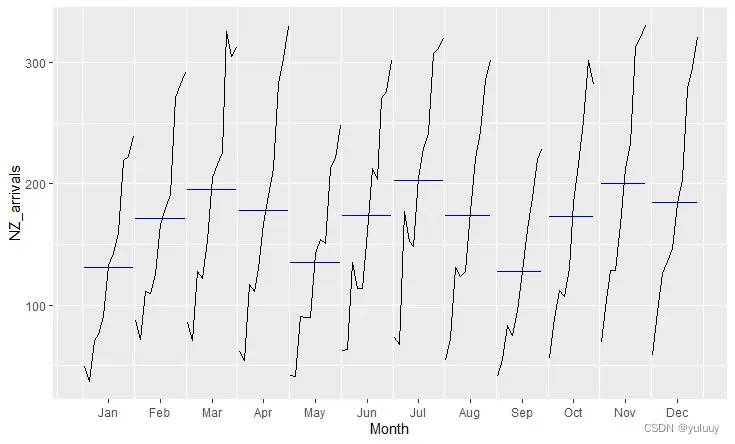
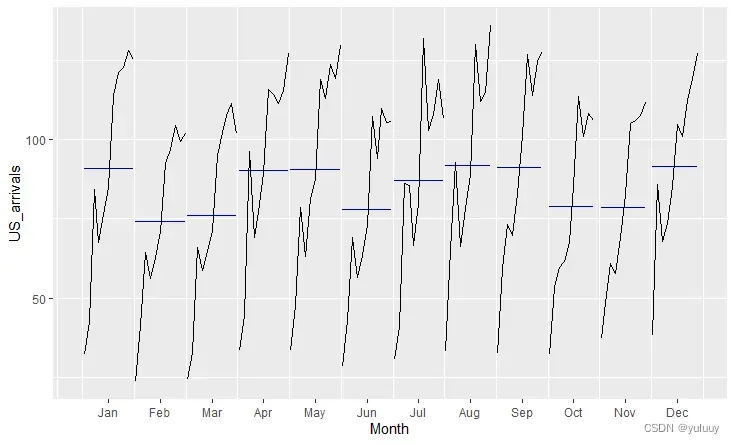
#dj道琼斯指数的日变化类似一个白噪声吗?
ddj<-diff(dj)#道琼斯指数的日变化量
autoplot(ddj)
ggAcf(ddj) 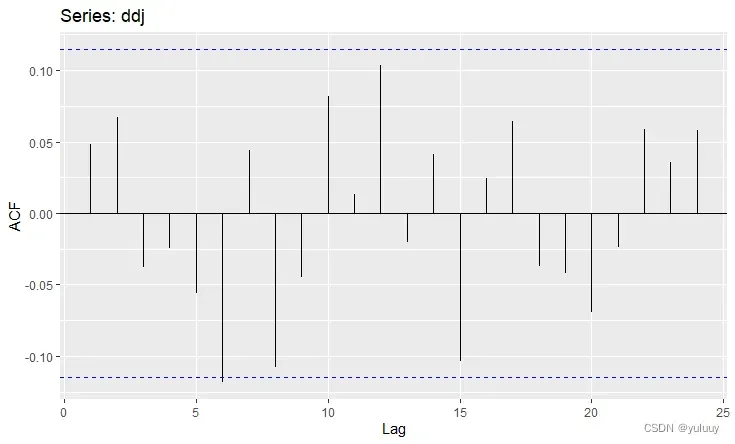
由图所示,道琼斯指数的自相关值基本都处在边界值之内, 所以很有可能是一个白噪音序列,表明序列中没有任何可以利用的动态规律。
文章出处登录后可见!