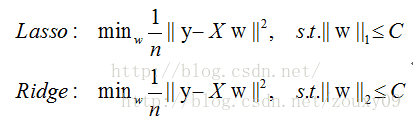正则化的相关理解

正则化（Regularization）是机器学习中一种常用的技术，其主要目的是控制模型复杂度，减小过拟合。

我们结合前面讨论过的损失函数的定义来讨论正则化问题，下面是加入正则项的损失函数：

$\sum_{i=1}^{N}\left ( y_{i}-f(x_{i}) \right )^{2}+r(w)$

正则化的本质是为损失函数加入一个正则项（Regularization）这里是 $r(w)$ ，这个正则项可以理解为一个惩罚项，它的自变量是权重向量 $\omega$ ，我们的最终目的是为了最小化loss function，也就是说我们也需要最小化正则项的影响。

但是这里有一个需要注意的点，我们如何减小loss function呢？当然是通过 $f(x_{i})$ 去拟合训练集的数据分布，越要拟合训练集的数据分布我们可能需要越多的多项式项，也就需要越多的参数 $w$ ，于是我们的正则项 $r(w)$ 就会越大，loss function就会越大，这和我们的本意减小loss function相冲突，于是我们需要找到 $f(x_{i})$

接下来我们从正则项的目的去对它进行探究，我们都知道正则化的目的是为了避免过拟合

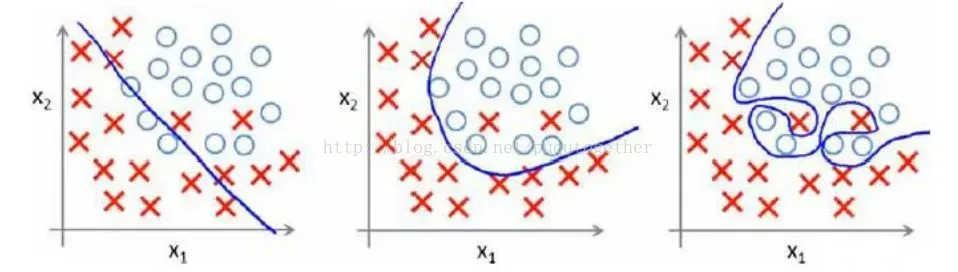
首先，用一个例子来理解什么是过拟合，假设我们要根据特征分类{男人X，女人O}。

请看下面三幅图，x1、x2、x3；

1、图x1明显分类的有点欠缺，有很多的“男人”被分类成了“女人”。

2、图x2虽然有两个点分类错误，但是能够理解，毕竟现实世界有噪音干扰，比如有些人男人留长发、化妆、人妖等等。

3、图x3分类全部是正确的，但是看着这副图片，明显觉得过了，连人妖都区分的出来，可想而知，学习的时候需要更多的参数项，甚至将生殖器官的形状、喉结的大小、有没有胡须特征等都作为特征取用了，总而言之f(x)多项式的N特别的大，因为需要提供的特征多，或者提供的测试用例中我们使用到的特征非常多(一般而言，机器学习的过程中，很多特征是可以被丢弃掉的)。

好了，总结一下三幅图：

x1我们称之为【欠拟合】

x2我们称之为【分类正拟合】，随便取的名字，反正就是容错情况下刚好的意思。

x3我们称之为【过拟合】，这种情况是我们不希望出现的状况，为什么呢？很简单，它的分类只是适合于自己这个测试用例，对需要分类的真实样本而言，实用性可想而知的低。

为了避免过拟合，我们需要尽量简化f(x)的形式，也就是需要尽量少的多项式项x，也就意味着需要尽量少的参数w。

现在知道这些信息之后，如何去防止过拟合，我们首先想到的就是控制多项式的数量，即让N最小化吧，而让N最小化，其实就是让W向量中项的个数最小化吧？

其中， $W=([w_{0},w_{1},w_{2}...])$

PS: 可能有人会问，为什么是考虑W，而不是考虑X?很简单，你不知道下一个样本想x输入的是什么，所以你怎么知道如何去考虑x呢？相对而言，在下一次输入 $x^{^{k}}$ ,即第k个样本之前，我们已经根据次测试样本的输入计算(学习)出了W.

L0正则，L1正则和L2正则分布又是什么呢？

L0正则化的值是模型参数中非零参数的个数。

L1正则化表示各个参数绝对值之和。

L2正则化标识各个参数的平方的和的开方值

L0正则我们可以很好理解，当模型参数w为0是，输入的特征项无论是多少都不会体现在拟合曲线上，因为 $0x_{i}$ 没有啥意义，说明 $x_{i}$ 项没有任何权重。从直观上看，利用非零参数的个数，可以很好的来选择特征，实现特征稀疏的效果，具体操作时选择参数非零的特征即可。但因为L0正则化很难求解，是个NP难问题，因此一般采用L1正则化。L1正则化是L0正则化的最优凸近似，比L0容易求解，并且也可以实现稀疏的效果。

L1正则化 $r(w)=\gamma\left | x \right |_{1}$ 在实际中往往替代L0正则化，来防止过拟合。在江湖中也人称Lasso。L1正则化之所以可以防止过拟合，是因为L1范数就是各个参数的绝对值相加得到的，我们前面讨论了，参数值大小和模型复杂度是成正比的。因此复杂的模型，其L1范数就大，最终导致损失函数就大，说明这个模型就不够好。

L2正则化 $r(w)=\frac{\gamma }{2}\left \| x \right \|^{2}$ 可以防止过拟合的原因和L1正则化一样，只是形式不太一样。

L2范数是各参数的平方和再求平方根，我们让L2范数的正则项最小，可以使W的每个元素都很小，都接近于0。但与L1范数不一样的是，它不会是每个元素为0，而只是接近于0。越小的参数说明模型越简单，越简单的模型越不容易产生过拟合现象。L2正则化江湖人称Ridge，也称“岭回归”

L1正则我们可理解为每次权重w更新是减去一个常数，它是又可能减到0的，所以它可以达到稀疏的效果；而L2正则是每次更新权重w按照百分比减，它无法减到0，所以无法达到稀疏。

总结：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。在所有特征中只有少数特征起重要作用的情况下，选择Lasso比较合适，因为它能自动选择特征。而如果所有特征中，大部分特征都能起作用，而且起的作用很平均，那么使用Ridge也许更合适。

在机器学习中我们会将原本的损失函数 $\sum_{i=1}^{N}\left ( y_{i}-f(x_{i}) \right )^{2}$ 叫做经验风险，而正则项和前者的组合 $\sum_{i=1}^{N}\left ( y_{i}-f(x_{i}) \right )^{2}+r(w)$ 叫做结构风险，所以顺其自然的正则化就是我们将结构风险最小化的过程。