1，无约束优化问题（unconstrained optimization）

$\underset{x{\in}\mathbb{R}^{n}}{min}f(x)$

无优化约束问题：即找 $f(x)$ 函数在 $x\in \mathbb{R}^{n}$ 上的最小化的最优解 $x^{\ast }$ ， $f(x^{\ast })$ 问题

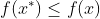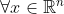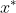（1）如果 $f(x^{\ast })\leq f(x)$ 且 $\forall{x\in \mathbb{R}^{n}}$ ，则 $x^{\ast }$ 为全局最优点—最小值点

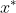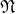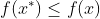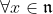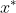（2）如果存在 $x^{\ast }$ 的一个邻域 $\mathfrak{N}$ ，使得 $f(x^{\ast })\leq f(x)$ 且 $\forall{x\in \mathfrak{n}}$ ，则称 $x^{\ast }$ 为局部最优点—极小值点

Theorem.1：局部极小值点，一阶导为0

Theorem.2： $\bigtriangledown^{2}f(x)$ ，海瑟矩阵半正定（positive semidefinite）

Theorem.3：（二阶充分条件）若 $\bigtriangledown{f(x^{\ast })}=0$ ， $\bigtriangledown^{2}f(x^{\ast })$ is positive definite，则 $x^{\ast }$ 是局部极小值点—判断最优解的法则

Theorem.4：若 $f$ 为凸函数，则任意一个极小值点为全局极小值点

note：非凸函数—遗传算法/离子群算法（启发式方法，无理论）

期待跳出局部极值，达到全局极值

2，线搜索方法（line search）

（1）概念：

构造一系列收敛序列 $\left \{ x_{k} \right \}$ 收敛到最优点 $x^{\ast }$ ，每次对于当前的状态 $x_{k}$ ，选择优化方向 $P_{k}$ ，以及最优步长 $\alpha$ ，最终使得 $\underset{\alpha > 0}{min}f(x_{k}+\alpha P_{k})$

${\color{Red} x_{k}\rightarrow x^{\ast }}$ ${\color{Red}x_{k+1}=x_{k}+\alpha P_{k} }$

（2）方法：

在线搜索（line search）方法中，主要的迭代为

$x_{k+1}=x_{k}+\alpha P_{k}$

成功的线搜索方法取决于方向 $P_{k}$ 和步长（step length） $\alpha _{k}$ 的选择。

大多数线搜索算法中，要求 $P_{k}$ 是一个下降方向（descent direction），即 $P_{k}^{T}\bigtriangledown{f_{k}}< 0$ （梯度与 $P_{k}$ 点积小于0），一般而言，要求线搜索的方向有下述形式

$P_{k}=-B_{k}^{-1}\bigtriangledown{f_{k}}$

其中 $B_{k}$ 是一个对称正定的满秩矩阵（symmetric and nonsingulear）， $\bigtriangledown{f_{k}}| _{x=x_{k}}$ 是梯度（梯度是上升最快的方向）

【1】steepest descent method：I（单位矩阵） $-\bigtriangledown{f_{k}}$ — 最速下降法

【2】Newton’s method：the exact Hessian $\bigtriangledown^{2}f(x_{k})$ — 海瑟矩阵估计法

【3】Quasi-Newton method：an approximation to the Hessian that is updated at every iteration by means of a low-rank formula. — 拟牛顿法（为了避开海瑟矩阵求逆）

note：点积 $\left \langle a;b \right \rangle=\left \| a \right \|\left \| b \right \|cos(a,b)$ ，正负取决于 $\overrightarrow{a}$ ， $\overrightarrow{b}$ 的夹角（象限左边为负，右边为正）