目录
线性判别分析
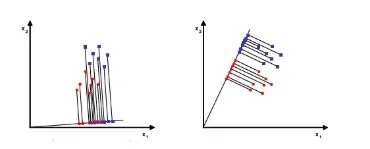
线性判别分析(LDA)是一种有监督的线性降维算法。与PCA不同,LDA是为了使降维后的数据点尽可能地容易被区分。
线性判别分析(LDA)的原理是对于给定的训练集,设法将样本投影到一条直线上,使得同类的投影点尽可能接近,异类样本的投影点尽可能远离;在对新样本进行分类时,将其投影到这条直线上,再根据投影点的位置来确定新样本的类别。PCA主要是从特征的协方差角度,去找到比较好的投影方式。LDA更多地考虑了标注,即希望投影后不同类别之间数据点的距离更大,同一类别的数据点更紧凑
LDA的降维过程
1、计算数据集中每个类别下所有样本的均值向量
2、通过均值向量,计算类间散布矩阵和类内散布矩阵
3、依据公式进行特征值求解,计算的特征向量和特征值
4、按照特征值排序, 选择前k个特征向量构成投影矩阵U
5、通过的特征值矩阵将所有样本转换到新的子空间中
案例:鸢尾花(Iris)
应用LDA技术对鸢尾花(Iris)的样本数据进行分析,鸢尾花数据集是20世纪30年代的经典数据集,它由Fisher收集整理,数据集包含150个数据集,分为3类,每类50个数据,每个数据包含4个属性。可通过花萼长度、花萼宽度、花瓣长度和花瓣宽度4个属性预测鸢尾花卉属于山鸢尾(Iris Setosa)、杂色鸢尾(Iris Versicolour)、维吉尼亚鸢尾(Iris Virginica)中的哪种类别,将类别文字转化为数字类别。

数据集中有4个特征,萼片长、萼片宽、花瓣长和花瓣宽,总共150行,每一行是一个样本,这就构成了一个4×150的输入矩阵,输出是1列,即花的类别,构成了1×150的矩阵。分析的目标就是通过LDA算法将输入矩阵映射到低维空间中进行分类。
代码演示
import pandas as pd
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv('iris.data.txt', header=None)
df[4] = df[4].map({'Iris-setosa':0, 'Iris-versicolor':1, 'Iris-virginica':2})
print(df.tail())
y, X = df.iloc[:, 4].values, df.iloc[:, 0:4].values
X_cent = X - X.mean(axis=0)
X_std = X_cent / X.std(axis=0)
import numpy as np
def comp_mean_vectors(X, y):
class_labels = np.unique(y)
n_classes = class_labels.shape[0]
mean_vectors = []
for cl in class_labels:
mean_vectors.append(np.mean(X[y==cl], axis=0))
return mean_vectors
def scatter_within(X, y):
class_labels = np.unique(y)
n_classes = class_labels.shape[0]
n_features = X.shape[1]
mean_vectors = comp_mean_vectors(X, y)
S_W = np.zeros((n_features, n_features))
for cl, mv in zip(class_labels, mean_vectors):
class_sc_mat = np.zeros((n_features, n_features))
for row in X[y == cl]:
row, mv = row.reshape(n_features, 1), mv.reshape(n_features, 1)
class_sc_mat += (row-mv).dot((row-mv).T)
S_W += class_sc_mat
return S_W
def scatter_between(X, y):
overall_mean = np.mean(X, axis=0)
n_features = X.shape[1]
print("n_features",n_features)
mean_vectors = comp_mean_vectors(X, y)
S_B = np.zeros((n_features, n_features))
for i, mean_vec in enumerate(mean_vectors):
n = X[y==i+1,:].shape[0]
mean_vec = mean_vec.reshape(n_features, 1)
overall_mean = overall_mean.reshape(n_features, 1)
S_B += n * (mean_vec - overall_mean).dot((mean_vec - overall_mean).T)
print("S_B:",S_B)
return S_B
def get_components(eig_vals, eig_vecs, n_comp=1):
n_features = X.shape[1]
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)
print("eig_pairs:",eig_pairs)
W = np.hstack([eig_pairs[i][1].reshape(4, 1) for i in range(0, n_comp)])
return W
S_W, S_B = scatter_within(X, y), scatter_between(X, y)
print(S_W)
eig_vals, eig_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
W = get_components(eig_vals, eig_vecs, n_comp=2)
print('EigVals: %s\n\nEigVecs: %s' % (eig_vals, eig_vecs))
print('\nW: %s' % W)
plt.xlabel('LD1')
plt.ylabel('LD2')
X_lda = X.dot(W)
for label,marker,color in zip(np.unique(y),('^', 's', 'o'),('blue', 'red', 'green')):
plt.scatter(X_lda[y==label, 0], X_lda[y==label, 1], c=color,edgecolors='black', marker=marker,s=640)
plt.show() #LD数
数据集
5.1,3.5,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
5.0,3.6,1.4,0.2,Iris-setosa
5.4,3.9,1.7,0.4,Iris-setosa
4.6,3.4,1.4,0.3,Iris-setosa
5.0,3.4,1.5,0.2,Iris-setosa
4.4,2.9,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.4,3.7,1.5,0.2,Iris-setosa
4.8,3.4,1.6,0.2,Iris-setosa
4.8,3.0,1.4,0.1,Iris-setosa
4.3,3.0,1.1,0.1,Iris-setosa
5.8,4.0,1.2,0.2,Iris-setosa
5.7,4.4,1.5,0.4,Iris-setosa
5.4,3.9,1.3,0.4,Iris-setosa
5.1,3.5,1.4,0.3,Iris-setosa
5.7,3.8,1.7,0.3,Iris-setosa
5.1,3.8,1.5,0.3,Iris-setosa
5.4,3.4,1.7,0.2,Iris-setosa
5.1,3.7,1.5,0.4,Iris-setosa
4.6,3.6,1.0,0.2,Iris-setosa
5.1,3.3,1.7,0.5,Iris-setosa
4.8,3.4,1.9,0.2,Iris-setosa
5.0,3.0,1.6,0.2,Iris-setosa
5.0,3.4,1.6,0.4,Iris-setosa
5.2,3.5,1.5,0.2,Iris-setosa
5.2,3.4,1.4,0.2,Iris-setosa
4.7,3.2,1.6,0.2,Iris-setosa
4.8,3.1,1.6,0.2,Iris-setosa
5.4,3.4,1.5,0.4,Iris-setosa
5.2,4.1,1.5,0.1,Iris-setosa
5.5,4.2,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.0,3.2,1.2,0.2,Iris-setosa
5.5,3.5,1.3,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
4.4,3.0,1.3,0.2,Iris-setosa
5.1,3.4,1.5,0.2,Iris-setosa
5.0,3.5,1.3,0.3,Iris-setosa
4.5,2.3,1.3,0.3,Iris-setosa
4.4,3.2,1.3,0.2,Iris-setosa
5.0,3.5,1.6,0.6,Iris-setosa
5.1,3.8,1.9,0.4,Iris-setosa
4.8,3.0,1.4,0.3,Iris-setosa
5.1,3.8,1.6,0.2,Iris-setosa
4.6,3.2,1.4,0.2,Iris-setosa
5.3,3.7,1.5,0.2,Iris-setosa
5.0,3.3,1.4,0.2,Iris-setosa
7.0,3.2,4.7,1.4,Iris-versicolor
6.4,3.2,4.5,1.5,Iris-versicolor
6.9,3.1,4.9,1.5,Iris-versicolor
5.5,2.3,4.0,1.3,Iris-versicolor
6.5,2.8,4.6,1.5,Iris-versicolor
5.7,2.8,4.5,1.3,Iris-versicolor
6.3,3.3,4.7,1.6,Iris-versicolor
4.9,2.4,3.3,1.0,Iris-versicolor
6.6,2.9,4.6,1.3,Iris-versicolor
5.2,2.7,3.9,1.4,Iris-versicolor
5.0,2.0,3.5,1.0,Iris-versicolor
5.9,3.0,4.2,1.5,Iris-versicolor
6.0,2.2,4.0,1.0,Iris-versicolor
6.1,2.9,4.7,1.4,Iris-versicolor
5.6,2.9,3.6,1.3,Iris-versicolor
6.7,3.1,4.4,1.4,Iris-versicolor
5.6,3.0,4.5,1.5,Iris-versicolor
5.8,2.7,4.1,1.0,Iris-versicolor
6.2,2.2,4.5,1.5,Iris-versicolor
5.6,2.5,3.9,1.1,Iris-versicolor
5.9,3.2,4.8,1.8,Iris-versicolor
6.1,2.8,4.0,1.3,Iris-versicolor
6.3,2.5,4.9,1.5,Iris-versicolor
6.1,2.8,4.7,1.2,Iris-versicolor
6.4,2.9,4.3,1.3,Iris-versicolor
6.6,3.0,4.4,1.4,Iris-versicolor
6.8,2.8,4.8,1.4,Iris-versicolor
6.7,3.0,5.0,1.7,Iris-versicolor
6.0,2.9,4.5,1.5,Iris-versicolor
5.7,2.6,3.5,1.0,Iris-versicolor
5.5,2.4,3.8,1.1,Iris-versicolor
5.5,2.4,3.7,1.0,Iris-versicolor
5.8,2.7,3.9,1.2,Iris-versicolor
6.0,2.7,5.1,1.6,Iris-versicolor
5.4,3.0,4.5,1.5,Iris-versicolor
6.0,3.4,4.5,1.6,Iris-versicolor
6.7,3.1,4.7,1.5,Iris-versicolor
6.3,2.3,4.4,1.3,Iris-versicolor
5.6,3.0,4.1,1.3,Iris-versicolor
5.5,2.5,4.0,1.3,Iris-versicolor
5.5,2.6,4.4,1.2,Iris-versicolor
6.1,3.0,4.6,1.4,Iris-versicolor
5.8,2.6,4.0,1.2,Iris-versicolor
5.0,2.3,3.3,1.0,Iris-versicolor
5.6,2.7,4.2,1.3,Iris-versicolor
5.7,3.0,4.2,1.2,Iris-versicolor
5.7,2.9,4.2,1.3,Iris-versicolor
6.2,2.9,4.3,1.3,Iris-versicolor
5.1,2.5,3.0,1.1,Iris-versicolor
5.7,2.8,4.1,1.3,Iris-versicolor
6.3,3.3,6.0,2.5,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
7.1,3.0,5.9,2.1,Iris-virginica
6.3,2.9,5.6,1.8,Iris-virginica
6.5,3.0,5.8,2.2,Iris-virginica
7.6,3.0,6.6,2.1,Iris-virginica
4.9,2.5,4.5,1.7,Iris-virginica
7.3,2.9,6.3,1.8,Iris-virginica
6.7,2.5,5.8,1.8,Iris-virginica
7.2,3.6,6.1,2.5,Iris-virginica
6.5,3.2,5.1,2.0,Iris-virginica
6.4,2.7,5.3,1.9,Iris-virginica
6.8,3.0,5.5,2.1,Iris-virginica
5.7,2.5,5.0,2.0,Iris-virginica
5.8,2.8,5.1,2.4,Iris-virginica
6.4,3.2,5.3,2.3,Iris-virginica
6.5,3.0,5.5,1.8,Iris-virginica
7.7,3.8,6.7,2.2,Iris-virginica
7.7,2.6,6.9,2.3,Iris-virginica
6.0,2.2,5.0,1.5,Iris-virginica
6.9,3.2,5.7,2.3,Iris-virginica
5.6,2.8,4.9,2.0,Iris-virginica
7.7,2.8,6.7,2.0,Iris-virginica
6.3,2.7,4.9,1.8,Iris-virginica
6.7,3.3,5.7,2.1,Iris-virginica
7.2,3.2,6.0,1.8,Iris-virginica
6.2,2.8,4.8,1.8,Iris-virginica
6.1,3.0,4.9,1.8,Iris-virginica
6.4,2.8,5.6,2.1,Iris-virginica
7.2,3.0,5.8,1.6,Iris-virginica
7.4,2.8,6.1,1.9,Iris-virginica
7.9,3.8,6.4,2.0,Iris-virginica
6.4,2.8,5.6,2.2,Iris-virginica
6.3,2.8,5.1,1.5,Iris-virginica
6.1,2.6,5.6,1.4,Iris-virginica
7.7,3.0,6.1,2.3,Iris-virginica
6.3,3.4,5.6,2.4,Iris-virginica
6.4,3.1,5.5,1.8,Iris-virginica
6.0,3.0,4.8,1.8,Iris-virginica
6.9,3.1,5.4,2.1,Iris-virginica
6.7,3.1,5.6,2.4,Iris-virginica
6.9,3.1,5.1,2.3,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
6.8,3.2,5.9,2.3,Iris-virginica
6.7,3.3,5.7,2.5,Iris-virginica
6.7,3.0,5.2,2.3,Iris-virginica
6.3,2.5,5.0,1.9,Iris-virginica
6.5,3.0,5.2,2.0,Iris-virginica
6.2,3.4,5.4,2.3,Iris-virginica
5.9,3.0,5.1,1.8,Iris-virginica
局部线性嵌入
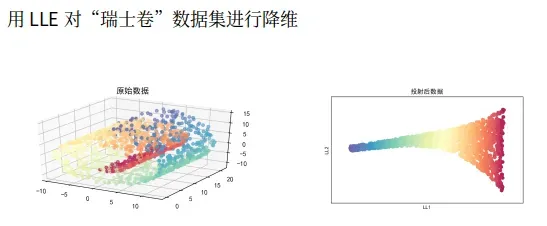
局部线性嵌入(LLE) 是一种非线性降维算法,它能够使降维后的数据较好地保持原有流形结构,每一个数据点都可以由其近邻点的线性加权组合构造得到。
局部线性嵌入寻求数据的低维投影,保留本地邻域内的距离。它可以被认为是一系列局部主成分分析,被全局比较以找到最佳的非线性嵌入。
算法的主要步骤分为三步
首先,寻找每个样本点的k个近邻点。
然后,由每个样本点的近邻点计算出该样本点的局部重建权值矩阵。
最后,由该样本点的局部重建权值矩阵和近邻点计算出该样本点的输出值。
LLE在有些情况下也并不适用,例如数据分布在整个封闭的球面上,LLE则不能将它映射到二维空间,且不能保持原有的数据流形。因此在处理数据时,需要确保数据不是分布在用合的球面或者椭球面上。
文章出处登录后可见!
