梯度下降法常用技巧

1、特征缩放（归一化）

作用：保证特征量在统一尺度

例如，特征x1是房子大小：0-1000平米，x2是卧室数量：1-5个，通过这两个特征得到的代价函数在计算时易导致梯度下降法来回震荡，下降速度较慢，如左图；因此，我们可以对这两组特征先进行归一化处理（除以最大值），将特征约束在0-1的范围：

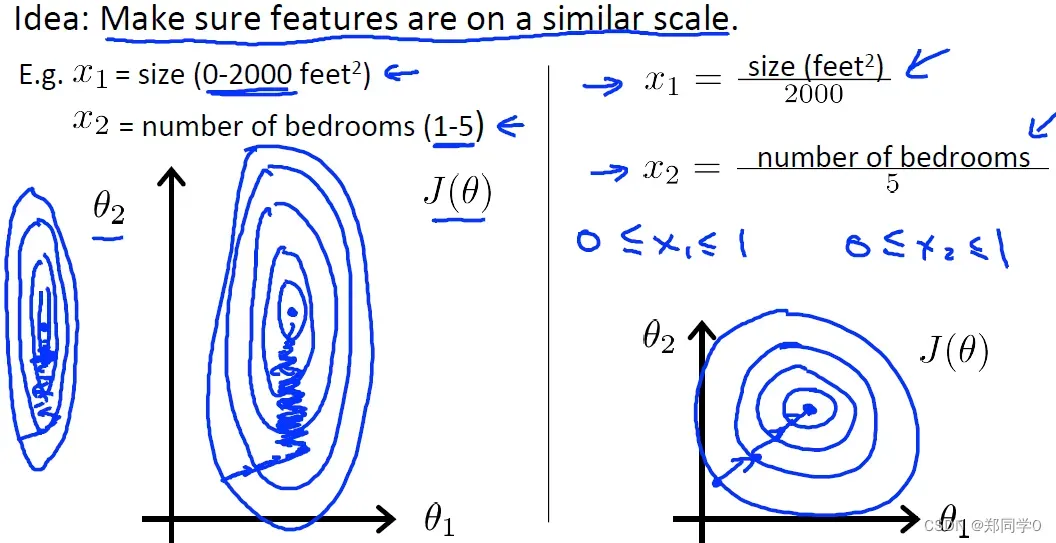
梯度下降法常用技巧

除了以上除以最大值的方法，还可以使用均值归一化：采用 $x_{i}-\mu _{_{i}}$ 代替 $x_{i}$ ，使特征具有接近0的均值：

$x_{1}=\frac{size-1000}{2000}$ ， $x_{2}=\frac{bedroom-2}{5}$

注意，归一化目的是为了运行更快，没必要太精确。

2、学习速率 $\alpha$

在训练时，考虑两个问题，1）如何确定梯度下降法是正常工作的；2）如何确定学习速率 $\alpha$ ；

判断梯度下降法是否收敛：保证每次迭代后的 $J(\Theta )$ 都是下降的。

自动收敛检测：当一次迭代后 $J(\Theta )$ 的下降小于阈值 $\varepsilon$ （通常取10^-3），可以认为达到收敛。但是 $\varepsilon$ 取值通常也是困难的。

对于学习速率 $\alpha$ 的取值，只要其足够小， $J(\Theta )$ 都会趋于min $J(\Theta )$ ，但是学习速率过小会导致收敛速度缓慢；因此，在选取学习速率值时，通常使用{…,0.001,0.003,0.01,0.03,0.1,0.3,1…}数值进行尝试，没选择一个 $\alpha$ ，画出其代价函数曲线，观察下降情况。

3、选择合适的特征

例如对房价进行预测，假设函数写为：

$h_{\theta}(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}$ ，

x1和x2分别表示房子的两个特征：长和宽，通常，我们使用面积来表示房子大小，因此我们可以直接使用面积（size）一个特征代替，假设函数即可转化为：

$h_{\theta}(x)=\theta_{0}+\theta_{1}x$ ，

通过数据观察，选择如下回归模型，能够较好拟合的多项式图像：

$h_{\theta}(x)=\theta_{0}+\theta_{1}x+\theta_{2}x^{2}+\theta_{3}x^{3}$ ，

此时，可以将x,x^2,x^3抽象为三个特征x1,x2,x3，其对应取值范围分别是1-1000，1-1000^2，1-1000^3，因此，要特别注意特征取值的尺度缩放。

4、正规方程法

该方法提供了一种求解参数 $\theta$ 的解析解法，一次性求得 $\theta$ 的最优值。

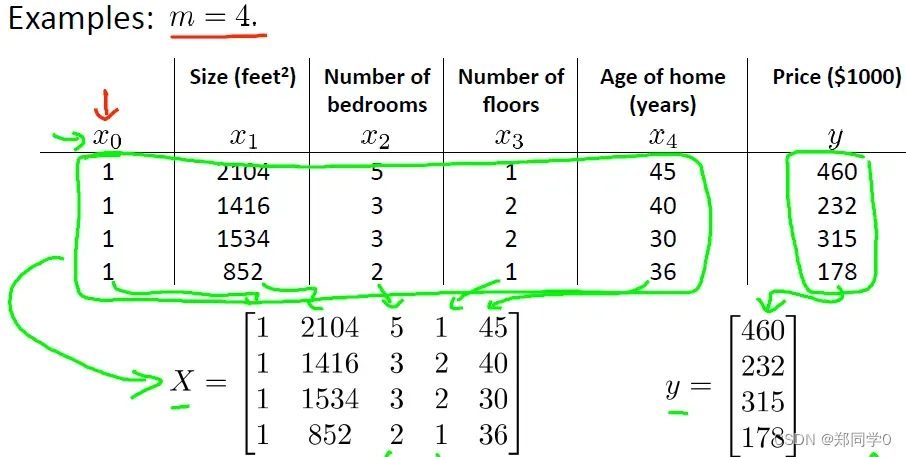
梯度下降法常用技巧

对上述样本数为4的一组数据，可以将特征量和目标量分别写成矩阵形式，然后使用正规方程：

$\Theta =(X^TX)^{-1}X^{T}\vec{y}$ ，求解 $\Theta$ ，并且不需要尺度缩放。

正规方程与梯度下降法相比，各自优缺点：

梯度下降法：	正规方程：
需要选择学习速率	无需选择
需要多次迭代	无需多次迭代
特征数量多时效果好	需要计算矩阵的逆，特征多时较复杂

因此，对于线性回归这种特定模型，在特征数量不大（ $n<10^4$ ）时，正规方程比梯度下降法具有更快的速度。

文章出处登录后可见！

已经登录？立即刷新

梯度下降法常用技巧

相关推荐