
混沌无形
混沌系统是世界本质,无形之中存在规律。机器人智能化发展从线性过渡到混沌,本号将分享机器人全栈技术(感知、规划、控制;软件、机械、硬件等)。
43篇原创内容
公众号
(文末提供原文PDF免费下载(期刊论文版式)
摘要:四轮驱动移动机器人(SSMR)在野外非结构化场景中有着广泛应用,本文对SSMR的运动规律及特性进行了详细分析;接着将SSMR运动模型抽象简化为两轮差速驱动机器人模型,构建了SSMR的运动学模型,并给出了简易的模型参数计算实验方案;最后从实际应用角度对比分析了SSMR和car-like robot、差速驱动机器人的优缺点及其适用范围。
01
![]()
引言
![]()
移动机器人种类繁多,但经典的“款型”也就只有几种,普通场景基本够用了。在野外非结构化环境中,比起《两轮差速驱动机器人》和《Car-like Robot》,四轮滑动转向驱动移动机器人(skid-steering mobile robot, SSMR)算是一匹黑马,把天赋展现得淋漓尽致。
作为本文的主角——四轮驱动移动机器人(SSMR),就是四个轮子都是独立驱动轮(简单想象,就是四个电机驱动对应的四个轮子),这能够提供强劲的马力,也就是越障能力超强,所以能够很好适应野外非结构化场景。需要注意的是,四轮驱动机器人主要分为两类:①滑动转向(Skid-steer Drive),即四个轮子是普通轮胎;②麦克纳姆轮转向,即四个轮子采用麦克纳姆轮。本文主要介绍前者,后者下回分解。
如图 1.1中的NERVA LG Robot就是采用四个电机驱动四个普通轮子,作为移动平台搭载各种传感器等设备,在野外环境执行侦察任务。

图 1.1 NERVA LG Robot
(图片来源: https://www.epequip.com/catalogue/unmanned-systems/unmanned-ground-vehicles/nerva-lg-versatile-light-robotic-system/)
一般地,采用滑动转向的四轮驱动机器人的结构简化后,就如图 1.2所示,其结构非常简单,只需要控制四个电机转动,则可控制机器人灵活运动。
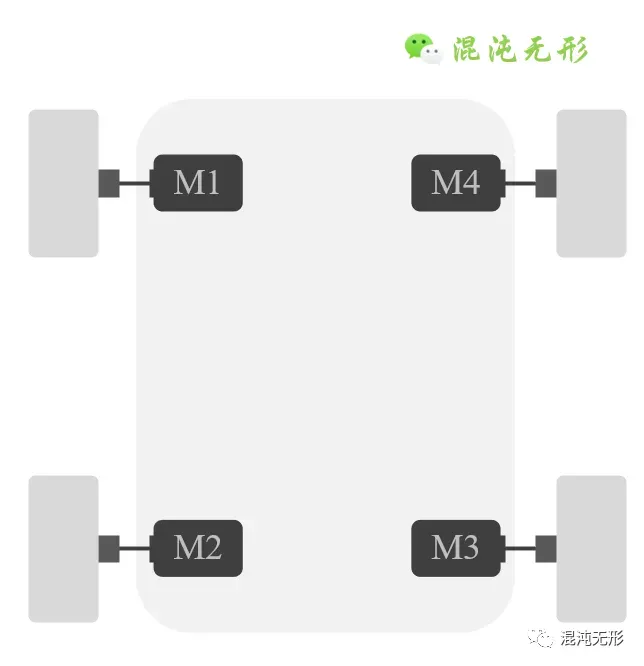
图 1.2 4WD(SSMR) robot构型. M1~4表示四个电机。
1
**问题:**为什么四轮驱动机器人的转向方式是滑动转向呢?
假如机器人的四个轮子速度相同,则机器人肯定是做直线运动;那假如四个轮子的速度不同,则会产生什么效果?这可参考之前的文章《两轮差速驱动机器人》的第二个问答。
如图 1.3所示,只要四个主动轮的转速不同,则会产生转向运动,一旦产生转向运动,意味着存在旋转中心(图中ICR),四个轮子与地面接触点(图中点A)的相对运动速度方向则如图 1.3所示,合速度方向与线段A-ICR相互垂直,而轮胎只能沿着纵向分速度方向转动,做速度分解可知,还存在沿轮子轴向(电机轴向)的横向分速度,由于四个轮胎的横向分速度大小不同,因此机器人会产生旋转分运动,而纵向分速度产生纵向分运动,合成运动则表现为机器人绕ICR做圆周运动。
进一步分析可知,**横向分速度是由轮胎与地面的滑动摩擦力产生的,纵向分速度是由轮胎与地面的滚动摩擦力产生的,所以转向运动是靠滑动摩擦产生的。**此外,还可知电机输出转矩驱动轮子转动,因此滚动摩擦是由电机主动产生的,而滑动摩擦是由于四个轮子速度不一致而被动产生的。
从力和力矩的角度理解:由于四个电机输出力矩不同,导致四个轮胎与地面接触点的作用力不同,尽管电机产生作用与轮胎的力的方向均沿着纵向方向,但大小不同,由于四个力的大小不同,也就意味着机器人不能平稳直线运动,肯定会产生车身的偏转,但由于轮胎只能滚动,所以转向运动就只能靠滑动了。
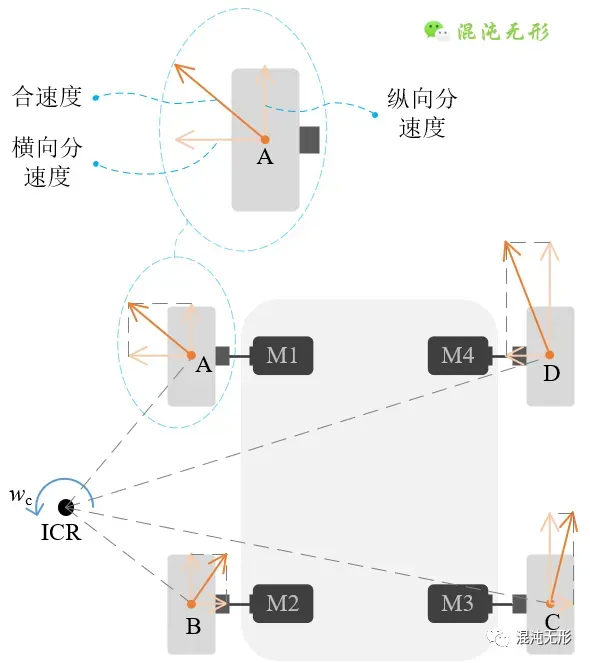
图 1.3 SSMR的速度分解.ICR(Instantaneous Center of Rotation)表示旋转中心.点A表示轮胎与地面的理想接触点.
通过对问题1的分析,我们知道四轮驱动机器人(SSMR)是靠滑动转向的,相比于滚动摩擦,滑动摩擦对轮胎的损耗极大,尤其是在水泥等硬质路面,如图 1.4所示,四轮驱动机器人在水泥路面留下的轮胎磨痕。所以四轮驱动机器人常被用于野外环境,因为泥土地面比较松软,滑动转向时对轮胎的磨损减小,且四个轮胎独立驱动,“抓地力”强,可“轻松”越过一般障碍。

图 1.4 SSMR自旋. 黑色圆圈是在硬质路面运动留下的轮胎磨痕,运动精度高才能画出标准正圆(图片来源:泰安硕宝智能科技有限公司产品)
基于上述分析,四轮驱动机器人(SSMR)做直线或圆周运动是由四个轮子的转速共同决定的,因此需要联合控制四个电机转动。那应该如何控制它按照开发者设定的参数运动呢?
这就需要对四轮驱动机器人(SSMR)进行运动学分析建模,尽管机器人的实际构型随着应用场景需求不同而有相应的变化,但运动模型原理都是一致的。因此,本文第2章将以图 2.1中的机器人构型进行运动模型分析,并抽象简化为图 2.4中的等效两轮差速驱动机器人模型,构建四轮驱动机器人(SSMR)的正逆运动学模型;第3章将结合ROS进行实验分析,并给出参数测量实验方案;第4章对比分析SSMR和car-like robot、差速驱动机器人的特点,最后进行总结和展望。
02
![]()
运动模型分析
![]()
2.1
机器人坐标系说明
在之前的文章中《两轮差速驱动机器人》和《Car-like Robot》均以几何中心为原点建立坐标系,这是因为低速运动状态下,两轮差速驱动机器人和car-like robot的轮子可近似认为几乎不会存在滑动摩擦,仅靠滚动摩擦便可实现旋转、平移等运动,(低速情况)可以不用引入动力学分析,而四轮驱动移动机器人(SSMR)建立坐标系具有一定的特殊性,因为它是通过滑动摩擦实现转向运动的,所以需要考虑机器人质量分布对机器人运动的影响。
为简化运动模型,这里做2个假设:①机器人轮子滚动时不产生空转现象;②机器人本体质量分布均匀,且质心(Center of Mass, COM)位于机器人几何纵向对称线上,但不一定位于几何横向对称线上。
如图 2.1所示,以机器人的几何中心为原点建立坐标系X-CENTER-Y,而以质心COM为原点建立坐标系X-COM-Y,两个坐标系X轴重合,Y轴平行,COM到CENTER的距离为_dcc_。机器人前向运动方向为X轴正方向(红色箭头),与之垂直向左为Y轴正方向(绿色箭头),Z轴垂直于纸面向外,满足右手定则。
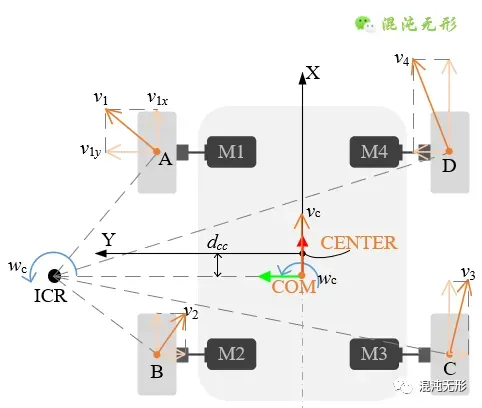
图 2.1 四轮驱动移动机器人(SSMR)运动模型. X-CENTER-Y表示机器人的几何中心坐标系,X-COM-Y表示机器人的质心坐标系.点A、B、C和D分别表示轮胎与地面的理想接触点。
2.2
运动模型规律分析
与两轮差速驱动机器人均存在非全向约束类似,四轮驱动移动机器人(SSMR)也是仅通过线速度、角速度[vc wc]T来描述其运动,二者的速度空间也相近,因此坐标系的建立方式、速度空间的定义和速度方向的约定是一致的,具体详情请回顾文章《两轮差速驱动机器人运动模型及应用分析》。
2
**问题:**为什么四轮驱动机器人(SSMR)的质心(COM)没有横向分速度vy呢?
这里笔者给出一个分析思路:运用我们高中物理知识,分析物体运动时,会找到该物体的质心来简化表达物体的运动。
假如四轮驱动移动机器人(SSMR)的质心存在横向分速度_vy_,意味着机器人(假想为质点)一边向前运动,一边旋转运动,同时还要向左(或右)运动。从前文问题1分析可知,前向运动是由轮子前向滚动产生的,而旋转运动是差速滑动产生的,那横向运动的速度是怎么产生的呢?总需要一个合成力来推动机器人横向运动吧,但是找不到!因为不可能四个轮子同时受到同向的横向摩擦力。
如图 2.1所示,两前轮受到向左的横向力,而两后轮受到向右的横向力,这两组横向力方向相反,恰好使得机器人绕着质心做旋转运动,也就是旋转中心是质心(这是质心的特性),叠加前向分运动,则表现为机器人做圆周运动。(这里可以脑补高中物理中电子在磁场中(或地球近似的)做圆周运动的情形)
通过上述分析可知,点COM只有沿X轴方向的线速度,以及角速度,且ICR位于坐标系X-COM-Y的Y轴上。对ICR位置的分析可参考文章《两轮差速驱动机器人运动模型及应用分析》。
从图 2.1可见,轮胎与地面的理想接触点(A、B、C和D)的合速度方向均垂直于旋转半径的径向方向,并可被分解为沿着轮子滚动方向的纵向分速度和沿着电机轴向的横向分速度。
规律:左(右)侧轮的_vx_是相同的,前(后)端轮的_vy_是相同的。
①左侧轮纵向分速度分析
如图 2.2所示,两个左侧轮与地面接触点的速度可表示为
其中,_v_1和_v_2分别表示点A和B的线速度,_r_1和_r_2分别对应其转弯半径。
而在RT△A-Q-ICR和RT△B-Q-ICR中,使用三角变换对公式(1)进行转换,表示为
式中,_α_1和_α_2分别表示A-ICR、B-ICR与Q-ICR的夹角。
在进一步对公式(2)化简,表示为
式中,_v_1_x_和_v_2_x_分别表示_v_1和_v_2的分速度。
基于上述分析可知,点A和B的纵向分速度是相同的,同理可分析知,点C和D的纵向分速度是相同的,但左侧和右侧轮的纵向分速度是不同的。
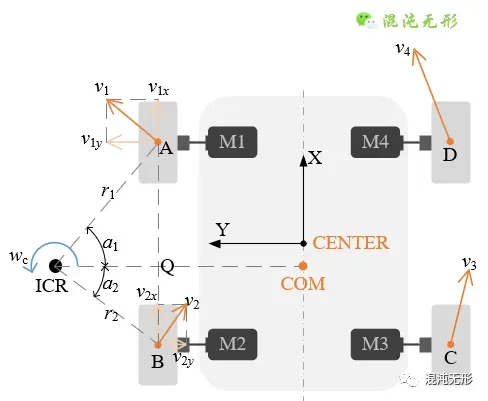
图 2.2 左侧轮纵向分速度示意图.线段AB与ICR-COM的交点为Q.
②前端轮横向分速度分析
采用两侧轮纵向分速度分析方法相同的思路,如图 2.3所示,两个前端轮与地面接触点的速度可表示为
其中,_v_4表示点D的线速度,_r_4对应其转弯半径。
而在RT△A-Q-ICR和RT△D-P-ICR中,使用三角变换对公式(4)进行转换,表示为
式中,_α_1和_α_4分别表示A-ICR、D-ICR与P-ICR的夹角。
因为AQ和DP长度相同,在进一步对公式(5)化简,表示为
式中,_v_1_y_和_v_4_y_分别表示_v_1和_v_4的分速度。
基于上述分析可知,点A和D的横向分速度是相同的,同理可分析知,点B和C的横向分速度是相同的,但前端和后端轮的横向分速度是不同的。
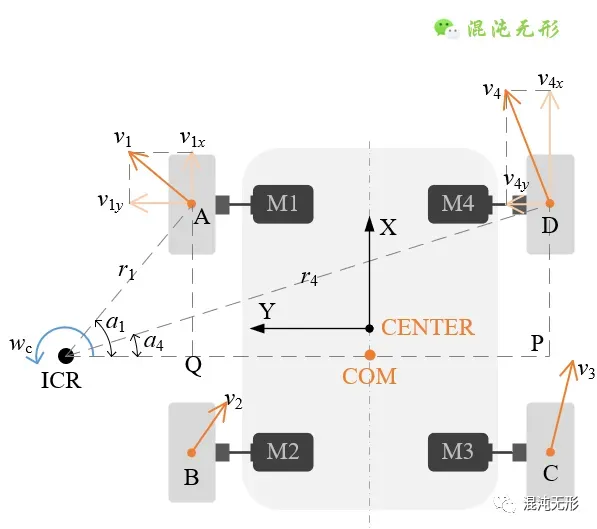
图 2.3 前端轮横向分速度示意图.线段DP与ICR-COM的交点为P.
③规律总结
通过上述①②步分析,其规律转化为下述方程
式中,_v__l_和_vr_分别表示左侧和右侧轮子的纵向分速度,_v__f_和_v__b_分别表示前端和后端轮子的横向分速度(见图 2.4)。
2.3
运动学模型建立
在章节2.2中分析了四轮驱动移动机器人(SSMR)的运动规律,那进一步应该如何建立其运动学模型呢?
这里的做法是将四轮驱动移动机器人(SSMR)的运动模型简化等效处理为两轮差速驱动机器人的运动模型。
如图 2.4所示,以ICR-COM为横轴线,以CENTER-COM为纵轴线,假设了虚拟左右轮的位置分别位于点L和R,这里需要注意的是虚拟轮间距LR的长度不一定等于真实轮间距QP的,且虚拟轮间距LR是动态变化的,笔者的分析如下:
假如没有旋转运动(无滑移),意味着只有_v__l_和_vr_,且_v__f_和_v__b_均为0,此时LR=QP;而如果存在旋转运动,也就是_v__f_和_v__b_不为0,存在滑移现象,则实际情况发生了变化,也就是说按照_v__l_和_vr_及PQ计算出来的角速度,并不是真实的角速度,而旋转分运动不同,滑移(滑动摩擦)程度不同,对实际的角速度影响也不同,因此虚拟轮间距LR是动态变化的,与滑动摩擦相关,因此不同摩擦系数的地面与轮胎接触,对实际旋转运动也是有着不同影响的。(这也是要实现精确控制的难点所在)
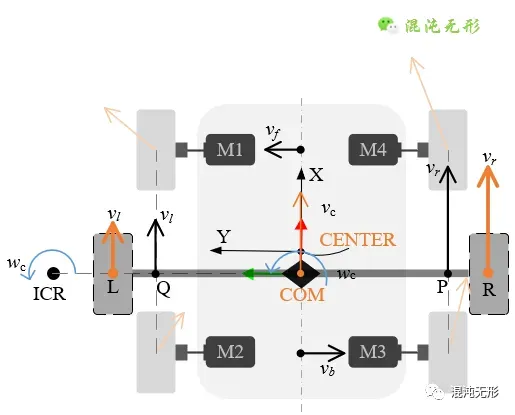
图 2.4 四轮驱动移动机器人(SSMR)模型简化等效示意图
笔者参考文献[2]的方法,对四轮驱动移动机器人(SSMR)进行运动学建模,其简化模型如图 2.5所示,套用《两轮差速驱动机器人运动模型及应用分析》的运动学模型推导方法,可得到下述关系
式中,_d_LR表示虚拟轮间距。
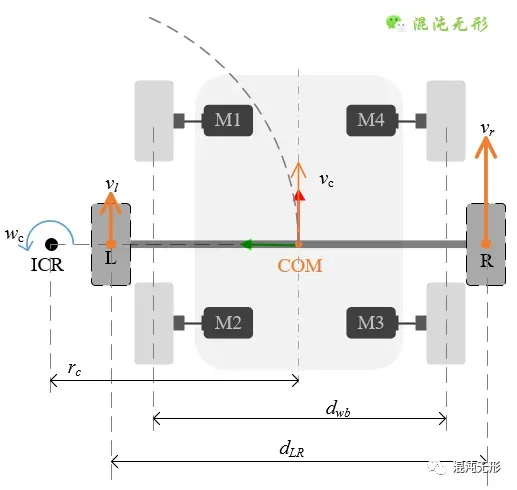
图 2.5 四轮驱动移动机器人(SSMR)简化模型.
若以虚拟的等效模型来表达运动模型,则四轮驱动移动机器人(SSMR)简化模型表示为:
简化正运动学模型是基于虚拟左右驱动轮的速度来计算几何质心COM的速度,可表示为
简化逆运动学模型是基于几何质心COM的速度分解出左右驱动轮的速度,可表示为
若采用公式(9-10)来描述四轮驱动移动机器人(SSMR),这里有两个点需要进一步讨论:
3
**问题:**在正运动学模型(9)中,左右虚拟轮的线速度vl和vr如何得到?
根据公式(7)可知,两左(或右)侧轮的纵向线速度大小与左(或右)虚拟轮的线速度相同。但两轮的实际转速可能不同。
从简化实际运动控制的角度出发,两左(或右)侧轮应该尽可能保持一致。这里做一个假象实验:若机器人的两前轮的速度相同,两后轮的速度相同,但前后轮的速度不同,机器人肯定是以介于前轮速度和后轮速度之间的某一速度直线运动,可想象前轮拖着后轮加快运动,后轮扯着前轮减缓运动。
所以无论前后轮的速度如何变化,机器人只会以一个速度运动,由于前后轮速度不相等会引起轮胎与地面在纵向上同时存在滚动和滑动摩擦,这会加速磨损轮胎,且不利于准确运动控制。所以,结论是尽可能保持两左(或右)侧轮速度相同,用数学语言描述就是:
式中,[_w_M1 _w_M2 _w_M3 _w_M4]表示对应轮子的转动角速度,[_R_M1 _R_M2 _R_M3 _R_M4]表示对应的轮子的半径。
4
**问题:**虚拟轮间距dLR具体是多少?
这也是四轮驱动移动机器人(SSMR)简化模型最难的一个参数,是一个随着工况变化的参数,且无法求得解析解。在参考文献[2]中给出的方法,是引入了无量纲参数_γ_:
式中,_d__wb_表示机器人的轮间距。
问题则转化为如何求_γ_,该参数与机器人的总负载、轮胎与地面的相对摩擦系数、转弯半径及质心位置都是有关系,是一个非常复杂的参数,所以常用的方法就是做实验,控制不再改动的机器人在特定地面上做差速转向运动,采集到多组实验数据后,拟合估算_γ_。
再回过头来看四轮驱动移动机器人(SSMR)运动学模型,基于公式(9-12)可知
正运动学模型为
逆运动学模型为
2.4
运动学模型应用
那问题来了,在实际中这两个模型(13-14)是怎么在实际工程中体现的呢?
套路和两轮差速驱动机器人相似,可参考《两轮差速驱动机器人运动模型及应用分析》。不同之处(也是难点)是需要精确控制4个电机转动,而上述推导是基于机器人质心COM来建模的,若想要基于几何中心CENTER来建立运动学模型,还需要做坐标变换(请读者自行转换)。
03
![]()
实验测试
![]()
ROS官网提供diff_drive_controller软件包[3],已经内置了四轮驱动移动机器人(SSMR)的正逆运动学模型,仅需要根据说明配置好参数后,便可控制Gazabo仿真器中的Husky或自己设计机器人了。diff_drive_controller运行后,会发送geometry_msgs/ Twist.msg,结构体内容包括沿着机器人质心坐标系_x-y-z_轴的线速度和角速度,具体为:
Vetor3 linear
float64 x
float64 y
float64 z
Vetor3 angular
float64 x
float64 y
float64 z
但对于两轮差速机器人而言,仅需两个参数:
沿x轴的线速度:linear. x = vc
绕z轴的角速度:angular.z = wc
如所示,通过[vc wc]T两个参数便可控制机器人在Rviz中运动。具体如何使用diff_drive_controller,以及控制机器人运动,可参考ROS官网,且其他博主也奉献了诸多实战经验和例程。(本文主要分析理论模型)
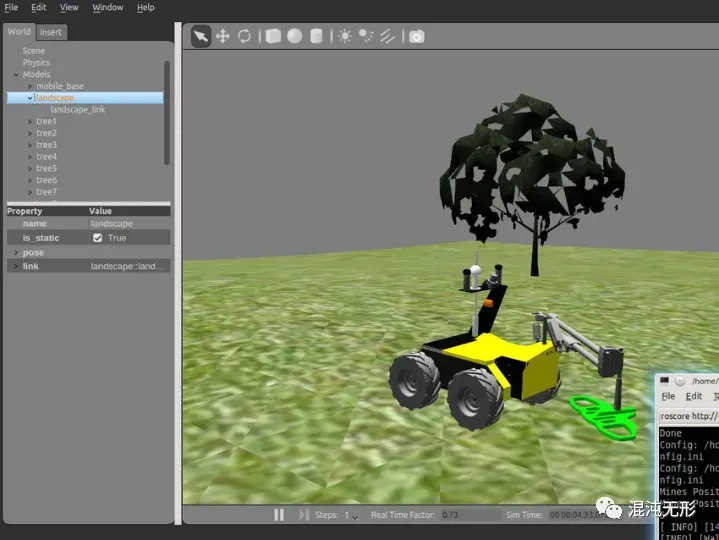
图 3.1 Gazabo中的HUSKY四轮驱动机器人.
(图片来源:https://www.researchgate.net/figure/Screenshot-of-Gazebo-simulating-the-Husky_fig2_283020710)
此外,这里笔者给出一种简单实用的测量参数γ的方法:
①在机器人上安装陀螺仪,用于测量机器人转动过程的角速度_wc_ 。
②精确控制机器人的四个轮子安装设定速度转动,保证两左(右)侧轮的转速相同,并通过编码器反馈数据计算虚拟轮子的线速度,v__l_和_vr。 ③利用公式(8)计算出此时的虚拟轮间距_d_LR,除以_d__wb_得到_γ_。
④绘制_γ_和[(v__l+vr)/( vr– v__l)](或_wc_)的数据图,并对数据曲线进行拟合,得到γ和[(v__l+vr)/( vr– v__l)](或_wc_)的关系表达式。
当机器人一旦转弯时,机载陀螺仪便可反馈实时机器人角速度,根据关系式得到对应的_γ_。当机器人通过陀螺仪采集完数据,且在实际应用时不允许使用陀螺仪,则在数据拟合阶段,对_γ_和[(v__l+vr)/( vr– v__l)]的进行拟合(也就是需要记录[v__l vr]),理论依据可参考公式(8)。
04
![]()
场景应用对比分析
![]()
通过上述对四轮驱动移动机器人(SSMR)的特点的详细分析,接下来对比SSMR与两轮差速驱动机器人、car-like robot的异同。
4.1
运动性能分析
SSMR的四个轮子大小相同,但四个轮子独立驱动,且结构前后、左右对称,因此SSMR的负载性能、越障性能要好于两轮差速驱动机器人和car-like robot。
在转弯过程中,SSMR是靠滑动实现的,这会对轮轴产生扭矩,而两轮差速驱动机器人和car-like robot却不会产生这种情况。
4.2
运动控制分析
从运动控制模型来看,SSMR的运动难以精确控制,因为存在严重的滑移情况,所以需要配合其他传感器来辅助检测机器人的运动情况。相较于两轮差速驱动机器人和car-like robot,SSMR需要同时控制四个电机的精确转动,其难度最高。
由于SSMR的质心和几何中心不重合,且质心位置难以确定,这也会导致控制模型不精确,因此在设计过程中,需要尽可能保证质心与几何中心相重合,可采用配置块来调节。
由于SSMR通过滑动摩擦实现转向,其受到的影响因素众多,这是对SSMR实现精确精确轨迹跟踪的一大挑战,需要考虑动力学进行综合分析。
总体来讲,在应用场景中,SSMR的特点是运动性能好、精确控制困难,因此多用于野外非结构化场景,最好为土质松软的地面(降低磨损),执行侦察、运输等任务。
05
![]()
结论及展望
![]()
本文从四轮驱动移动机器人(SSMR)的运动机理分析其运动规律,建立了四轮驱动移动机器人(SSMR)的运动模型,并深入分析了SSMR独有的运动特性。基于上述分析,将SSMR简化为两轮差速驱动机器人模型,推导了SSMR的较为完整运动控制模型,给出了重要参数计算的实验方案。从运动性能等方面分析了SSMR与car-like robot、两轮差速驱动机器人的异同之处,并说明SSMR的适用场景。
后面会持续更新其他类型的移动平台的分析,敬请期待。
参考资料
[1]https://groups.csail.mit.edu/drl/courses/cs54-2001s/skidsteer.html
[2]Wang T , Wu Y , Liang J , et al. Analysis and Experimental Kinematics of a Skid-Steering Wheeled Robot Based on a Laser Scanner Sensor[J]. Sensors (14248220), 2015, 15(5):9681-9702.
[3] http://wiki.ros.org/diff_drive_controller
福利放送
笔者为小伙伴们整理了期刊论文版式原文PDF,方便收藏和回味
链接:https://pan.baidu.com/s/16ehDAaeQUPkam4kMdwDkeA
提取码:lw05
若链接失效,可在后台回复关键字:13462FC或发送邮件:Zippen-Huang@outlook.com
相关声明
1.如果转载本文,文末务必注明:“转自微信公众号:混沌无形”
2.若有侵权,请联系作者
![]()
全文完,感谢阅读!!如果觉得写的不错,那就点个赞或者“在看”吧。

混沌无形
混沌系统是世界本质,无形之中存在规律。机器人智能化发展从线性过渡到混沌,本号将分享机器人全栈技术(感知、规划、控制;软件、机械、硬件等)。
43篇原创内容
公众号
更多推荐
[
Car-like Robot运动模型及应用分析
](http://mp.weixin.qq.com/s?__biz=MzI3MTIyMjQwNQ==&mid=2247483758&idx=1&sn=751ade69c6323e9f445b2f09619ece81&chksm=eac45284ddb3db927a9435947af9f2ec2881b34d68ae3b92d74be03e5d709538f21f9f85f51d&scene=21#wechat_redirect)
文章出处登录后可见!
