文章目录

       我这次还是写的很细，并且破纪录了(哈哈哈)，虽然很累，但是我相信都是值得的，最后在这说一下我排的顺序，就是写作业的顺序，这样才好一点，就是4.3都写了，才能做出第小一问那个二分类，剩下的是自己根据那个二分类来调代码实现的，这样我感觉连贯一点。

        最后，疫情快过去了，河大加油，希望和老师早日线下见面(哈哈哈).

一、4.3 自动梯度计算

虽然我们能够通过模块化的方式比较好地对神经网络进行组装，但是每个模块的梯度计算过程仍然十分繁琐且容易出错。在深度学习框架中，已经封装了自动梯度计算的功能，我们只需要聚焦模型架构，不再需要耗费精力进行计算梯度。

飞桨提供了paddle.nn.Layer类，来方便快速的实现自己的层和模型。模型和层都可以基于paddle.nn.Layer扩充实现，模型只是一种特殊的层。继承了paddle.nn.Layer类的算子中，可以在内部直接调用其它继承paddle.nn.Layer类的算子，飞桨框架会自动识别算子中内嵌的paddle.nn.Layer类算子，并自动计算它们的梯度，并在优化时更新它们的参数。

pytorch中的相应内容是什么？请简要介绍。

       首先，这里要推出一个这个查了好久，才查到的东西。(个人认为比较好用）

       PyTorch 1.8 与 Paddle 2.0 API映射表-API文档-PaddlePaddle深度学习平台

       这个平台是飞浆官方推出的与torch的对照目录，这次是在几个函数的替代找了好久都没有的情况下，没办法，去网上查，然后问人，才发现了。感觉非常有用，强力推荐。

       好了言归正传，说一说对应的库。(nn.Layer对应的库就是nn.Module)

       这个是那个目录，这很轻易就可以找到想要的，所以强烈推荐。

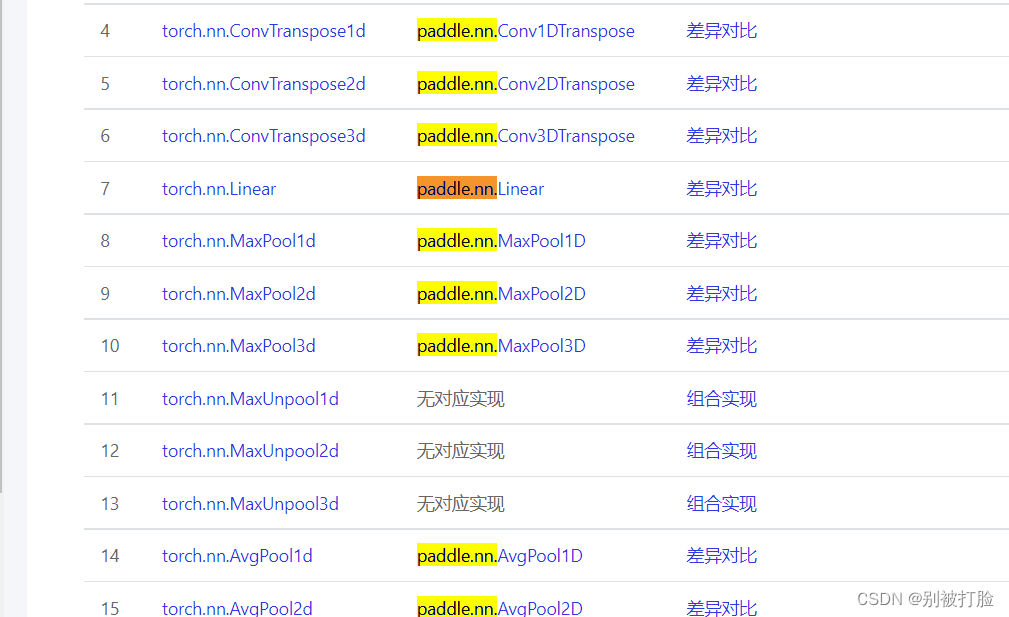
        为了方便大家，我再发一下老师，之前的发过的链接上的对应关系，这个简单些，也方便查一些。(但是，还是建议大家查我上边发的文档）

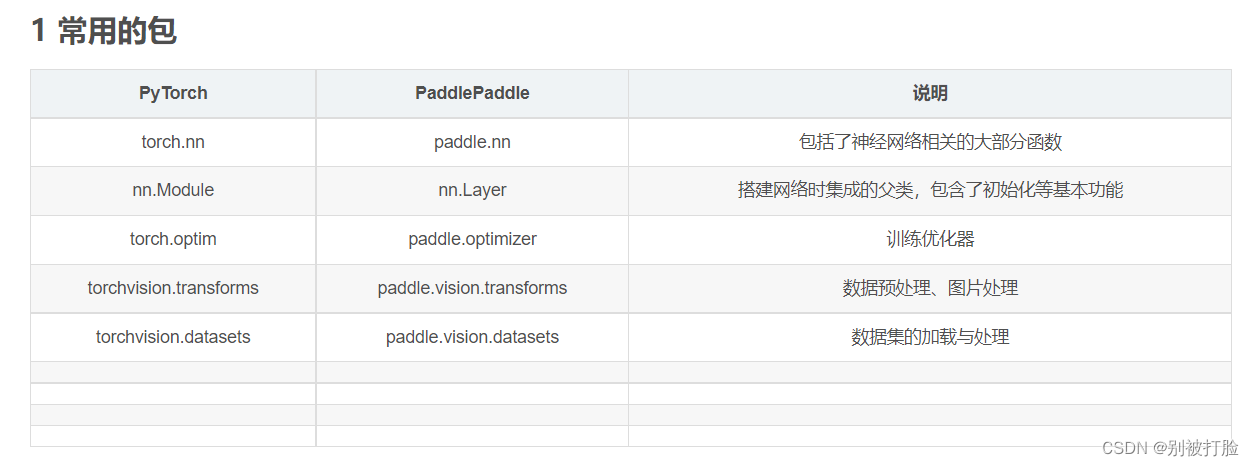
          当然，如果想要具体的看看函数的用法，还是要请出pytorch官方文档。(点飞浆的Linear的文档，也是会跳转到pytorch的。)

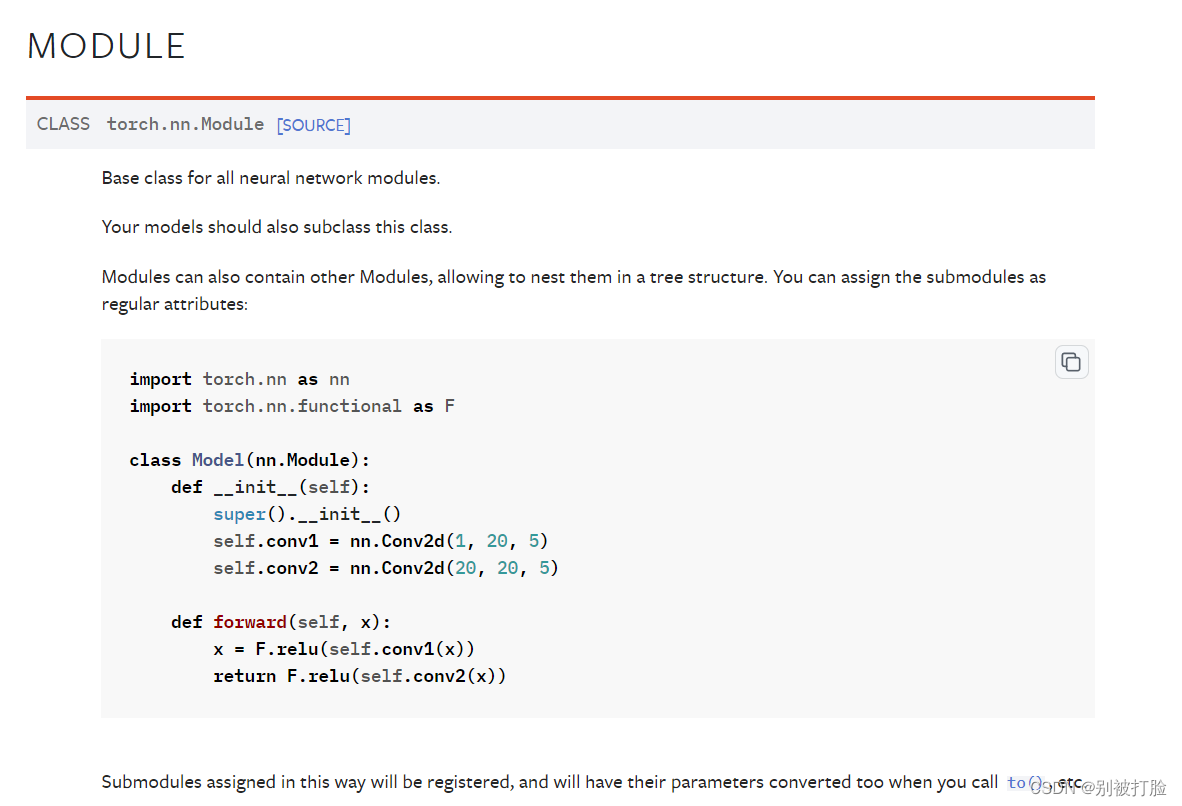
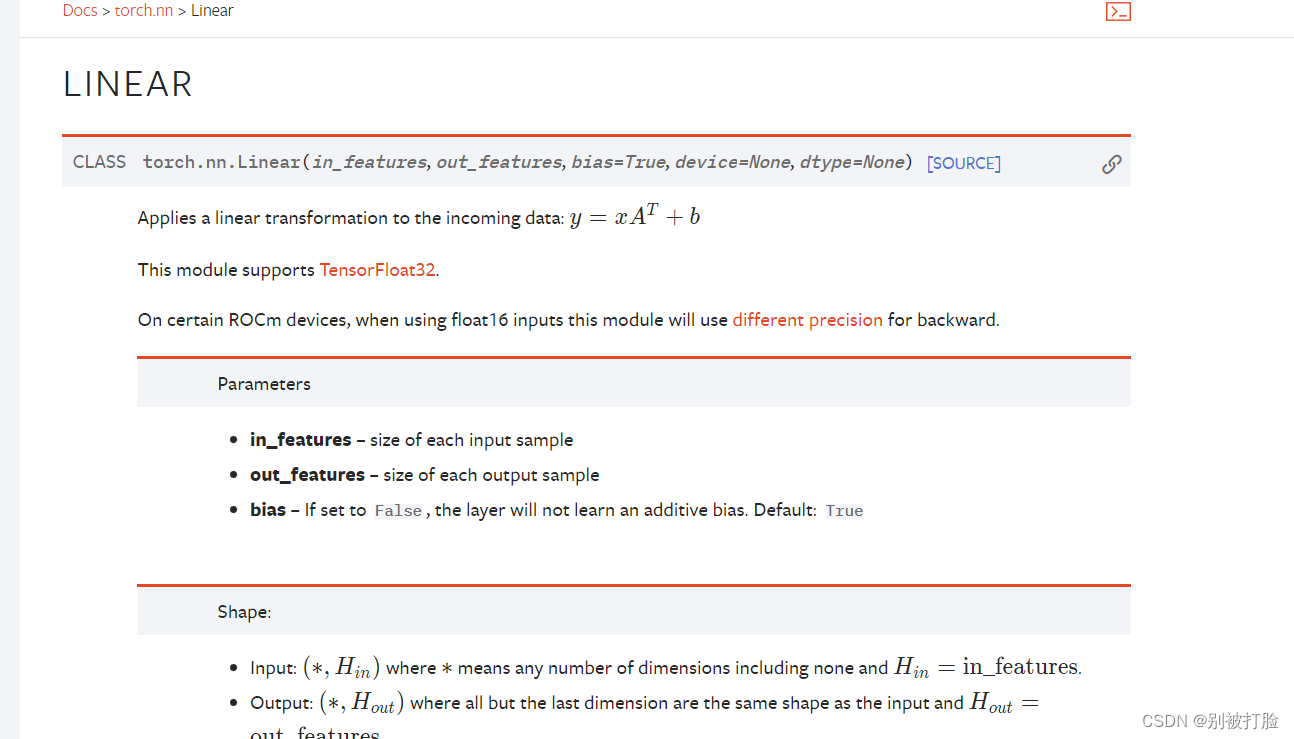
       这个就是了，建议大家去看一看，像linear之前的用法，我在前边的文档中就说过了，现在主要是说一说Module库的好处。

•  包装torch普通函数和torch.nn.functional专用于神经网络的函（torch.nn.functional是专门为神经网络所定义的函数集合）
• 只需要重新实现__init__和forward函数，求导的函数是不需要设置的，会自动按照求导规则求导(Module类里面是没有定义backward这个函数的）
• 可以保存参数和状态信息；

        nn.Module的用法是:

• 最好记住一些类似于named_parameters()这样的函数，这样的函数才能体现优越性。
• 需要继承nn.Module类，并实现forward方法；
• 一般把网络中具有可学习参数的层放在构造函数__init__()中；
• 不具有可学习参数的层(如ReLU)可在forward中使用nn.functional来代替；
• 只要在nn.Module的子类中定义了forward函数，利用Autograd自动实现反向求导。

  4.3.1 利用预定义算子重新实现前馈神经网络 

(1. 使用pytorch的预定义算子来重新实现二分类任务。（必做）)

# coding=gbk
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.init import constant_, normal_, uniform_
import torch
from nndl import make_moons
from metric import accuracy
import matplotlib.pyplot as plt
import math

       这里先说一下，用到的库，并且注意上边#后边的，一定要注意解码方式，最好要规定，要不然写注释的时候，有可能会报错。 

       然后，说一下，定义的神经网络。

class Model_MLP_L2_V2(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V2, self).__init__()
        # 使用'paddle.nn.Linear'定义线性层。
        # 其中第一个参数（in_features）为线性层输入维度；第二个参数（out_features）为线性层输出维度
        # weight_attr为权重参数属性，这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
        # bias_attr为偏置参数属性，这里使用'paddle.nn.initializer.Constant'进行常量初始化
        self.fc1 = nn.Linear(input_size, hidden_size)
        w1 = torch.empty(hidden_size,input_size)
        b1=  torch.empty(hidden_size)
        self.fc1.weight=torch.nn.Parameter(normal_(w1,mean=0.0, std=1.0))
        self.fc1.bias=torch.nn.Parameter(constant_(b1,val=0.0))
        self.fc2 = nn.Linear(hidden_size, output_size)
        w2 = torch.empty(output_size,hidden_size)
        b2 = torch.empty(output_size)
        self.fc2.weight=torch.nn.Parameter(normal_(w2,mean=0.0, std=1.0))
        self.fc2.bias=torch.nn.Parameter(constant_(b2,val=0.0))
        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = F.sigmoid

    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        return a2

   代码的大致思想：

           其实，这个就是一个linear就是一层，需要注意的就是，像w和b都是linear中的参数，最好按我上边的方法定义，并且forward函数，就是我之前说过的，在里边写传输的过程。

   需要注意的函数：

          需要注意的就是torch.nn.init函数了，这个函数去我发的文档里边就可以查到了，查这个是最难的，像定义w和b的形状，去官方文档中一查就行，官方文档都有          

  4.3.1.1 完善Runner类。

class RunnerV2_2(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        # 将模型切换为训练模式
        self.model.train()

        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)
        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")

        # log打印函数，如果没有传入则默认为"None"
        custom_print_log = kwargs.get("custom_print_log", None)

        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)
            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)

            # 自动计算参数梯度
            trn_loss.backward()
            if custom_print_log is not None:
                # 打印每一层的梯度
                custom_print_log(self)

            # 参数更新
            self.optimizer.step()
            # 清空梯度
            self.optimizer.zero_grad()

            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                self.save_model(save_path)
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")

    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def evaluate(self, data_set):
        # 将模型切换为评估模式
        self.model.eval()

        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss

    # 模型测试阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def predict(self, X):
        # 将模型切换为评估模式
        self.model.eval()
        return self.model(X)

    # 使用'model.state_dict()'获取模型参数，并进行保存
    def save_model(self, saved_path):
        torch.save(self.model.state_dict(), saved_path)

    # 使用'model.set_state_dict'加载模型参数
    def load_model(self, model_path):
        state_dict = torch.load(model_path)
        self.model.load_state_dict(state_dict)

代码的大致思想：

       这个就是用runner来运行函数，我在上一篇博客中把这个的思想写的非常详细，这个runner类与上一篇的几乎完全一样。

  4.3.1.2 模型训练

# 设置模型
input_size = 2
hidden_size = 5
output_size = 1
model = Model_MLP_L2_V2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 设置损失函数
loss_fn = F.binary_cross_entropy

# 设置优化器
learning_rate = 0.2
optimizer = torch.optim.SGD(params=model.parameters(),lr=learning_rate)

# 设置评价指标
metric = accuracy

# 其他参数
epoch_num = 3000
saved_path = "best_model.pdparams"

# 实例化RunnerV2类，并传入训练配置
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_path="best_model.pdparams")

运行结果为：

[Evaluate] best accuracy performence has been updated: 0.00000 –> 0.46250
[Train] epoch: 0/3000, loss: 0.6551498174667358
[Evaluate] best accuracy performence has been updated: 0.46250 –> 0.60625
[Evaluate] best accuracy performence has been updated: 0.60625 –> 0.68750
[Evaluate] best accuracy performence has been updated: 0.68750 –> 0.72500
[Train] epoch: 50/3000, loss: 0.5103745460510254
[Evaluate] best accuracy performence has been updated: 0.72500 –> 0.73125
[Evaluate] best accuracy performence has been updated: 0.73125 –> 0.73750
[Train] epoch: 100/3000, loss: 0.42853039503097534
[Evaluate] best accuracy performence has been updated: 0.73750 –> 0.74375
[Evaluate] best accuracy performence has been updated: 0.74375 –> 0.75000
[Evaluate] best accuracy performence has been updated: 0.75000 –> 0.75625
[Evaluate] best accuracy performence has been updated: 0.75625 –> 0.76250
[Train] epoch: 150/3000, loss: 0.37542006373405457
[Evaluate] best accuracy performence has been updated: 0.76250 –> 0.76875
[Evaluate] best accuracy performence has been updated: 0.76875 –> 0.77500
[Evaluate] best accuracy performence has been updated: 0.77500 –> 0.78125
[Train] epoch: 200/3000, loss: 0.3404920995235443
[Evaluate] best accuracy performence has been updated: 0.78125 –> 0.78750
[Train] epoch: 250/3000, loss: 0.31656843423843384
[Train] epoch: 300/3000, loss: 0.2997353672981262
[Evaluate] best accuracy performence has been updated: 0.78750 –> 0.79375
[Evaluate] best accuracy performence has been updated: 0.79375 –> 0.80000
[Train] epoch: 350/3000, loss: 0.287742555141449
[Train] epoch: 400/3000, loss: 0.2791396677494049
[Evaluate] best accuracy performence has been updated: 0.80000 –> 0.80625
[Train] epoch: 450/3000, loss: 0.2729260325431824
[Evaluate] best accuracy performence has been updated: 0.80625 –> 0.81250
[Train] epoch: 500/3000, loss: 0.26839905977249146
[Train] epoch: 550/3000, loss: 0.2650667428970337
[Evaluate] best accuracy performence has been updated: 0.81250 –> 0.81875
[Train] epoch: 600/3000, loss: 0.2625855803489685
[Train] epoch: 650/3000, loss: 0.26071539521217346
[Evaluate] best accuracy performence has been updated: 0.81875 –> 0.82500
[Train] epoch: 700/3000, loss: 0.2592872381210327
[Train] epoch: 750/3000, loss: 0.2581814229488373
[Train] epoch: 800/3000, loss: 0.25731244683265686
[Train] epoch: 850/3000, loss: 0.25661858916282654
[Train] epoch: 900/3000, loss: 0.25605499744415283
[Train] epoch: 950/3000, loss: 0.25558871030807495
[Train] epoch: 1000/3000, loss: 0.25519540905952454
[Train] epoch: 1050/3000, loss: 0.25485676527023315
[Train] epoch: 1100/3000, loss: 0.25455909967422485
[Train] epoch: 1150/3000, loss: 0.254291832447052
[Train] epoch: 1200/3000, loss: 0.25404682755470276
[Train] epoch: 1250/3000, loss: 0.253817617893219
[Train] epoch: 1300/3000, loss: 0.25359901785850525
[Train] epoch: 1350/3000, loss: 0.25338679552078247
[Train] epoch: 1400/3000, loss: 0.25317731499671936
[Train] epoch: 1450/3000, loss: 0.25296729803085327
[Train] epoch: 1500/3000, loss: 0.2527539134025574
[Train] epoch: 1550/3000, loss: 0.25253432989120483
[Train] epoch: 1600/3000, loss: 0.252305805683136
[Train] epoch: 1650/3000, loss: 0.2520657181739807
[Train] epoch: 1700/3000, loss: 0.25181102752685547
[Train] epoch: 1750/3000, loss: 0.25153887271881104
[Train] epoch: 1800/3000, loss: 0.25124597549438477
[Train] epoch: 1850/3000, loss: 0.25092893838882446
[Train] epoch: 1900/3000, loss: 0.2505839467048645
[Train] epoch: 1950/3000, loss: 0.25020694732666016
[Evaluate] best accuracy performence has been updated: 0.82500 –> 0.83125
[Train] epoch: 2000/3000, loss: 0.2497936487197876
[Train] epoch: 2050/3000, loss: 0.24933934211730957
[Train] epoch: 2100/3000, loss: 0.2488391101360321
[Train] epoch: 2150/3000, loss: 0.2482878416776657
[Train] epoch: 2200/3000, loss: 0.24768006801605225
[Evaluate] best accuracy performence has been updated: 0.83125 –> 0.83750
[Train] epoch: 2250/3000, loss: 0.24701039493083954
[Train] epoch: 2300/3000, loss: 0.24627332389354706
[Train] epoch: 2350/3000, loss: 0.24546349048614502
[Train] epoch: 2400/3000, loss: 0.24457550048828125
[Train] epoch: 2450/3000, loss: 0.24360433220863342
[Train] epoch: 2500/3000, loss: 0.24254508316516876
[Train] epoch: 2550/3000, loss: 0.24139317870140076
[Train] epoch: 2600/3000, loss: 0.2401442527770996
[Train] epoch: 2650/3000, loss: 0.2387942522764206
[Train] epoch: 2700/3000, loss: 0.23733949661254883
[Train] epoch: 2750/3000, loss: 0.23577670753002167
[Evaluate] best accuracy performence has been updated: 0.83750 –> 0.84375
[Train] epoch: 2800/3000, loss: 0.23410315811634064
[Train] epoch: 2850/3000, loss: 0.2323170006275177
[Train] epoch: 2900/3000, loss: 0.23041728138923645
[Evaluate] best accuracy performence has been updated: 0.84375 –> 0.85000
[Train] epoch: 2950/3000, loss: 0.22840432822704315 

代码的大致思想：

        这个就是给对应的变量赋值，把数值带入运行一下。

需要注意的函数：

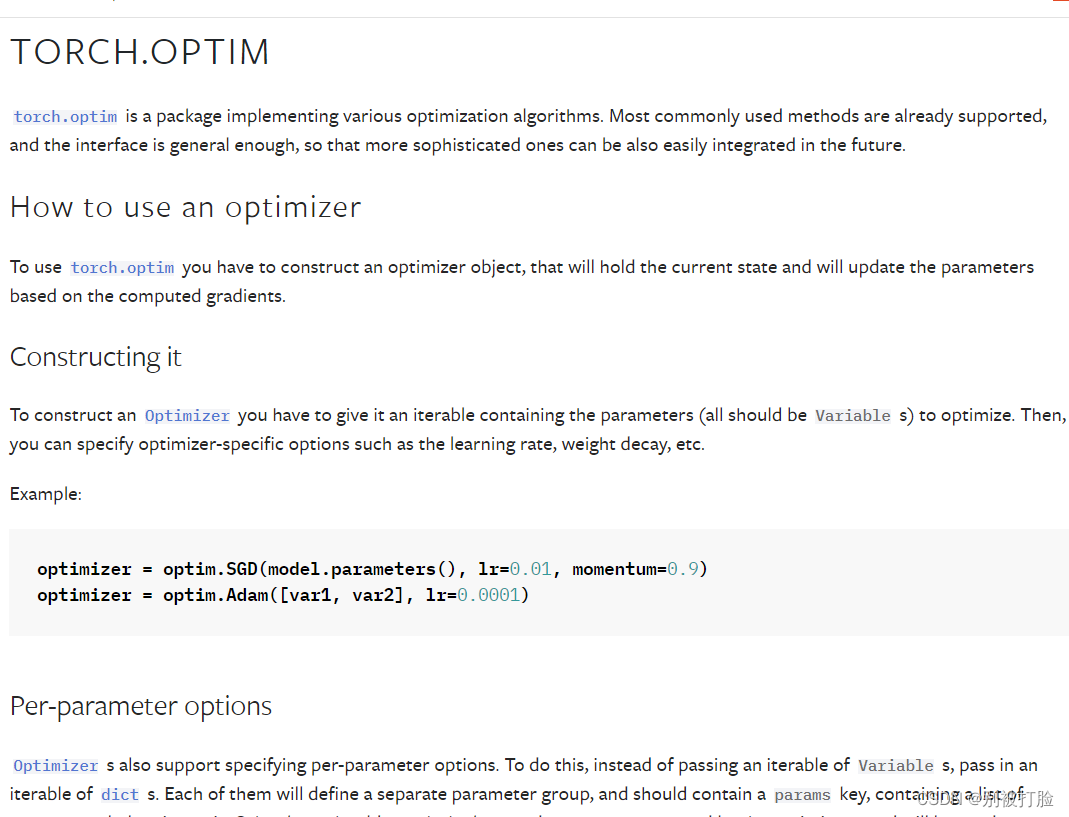
        这个需要注意一下torch.optim函数，这个函数的在torch中是十分重要的。强烈建议大家看一看。下边是官方文档。

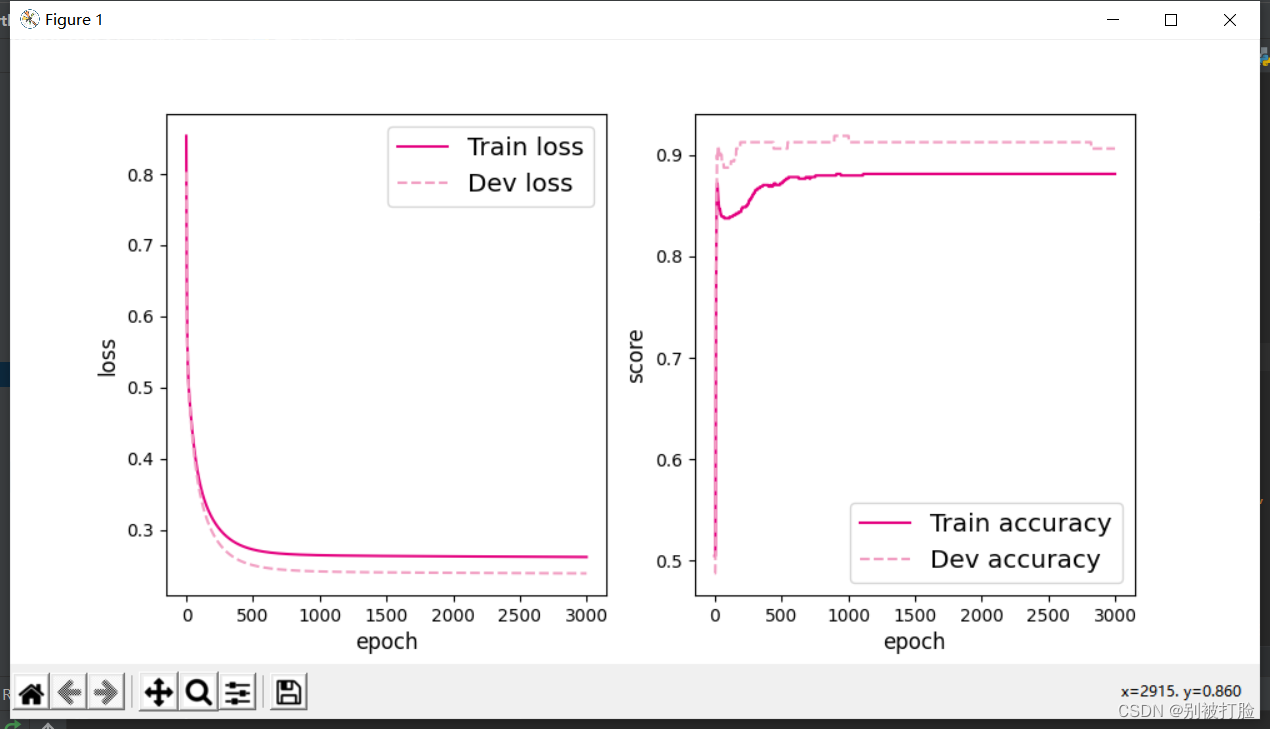
# 可视化观察训练集与验证集的指标变化情况
def plot(runner, fig_name):
    plt.figure(figsize=(10, 5))
    epochs = [i for i in range(0,len(runner.train_scores))]

    plt.subplot(1, 2, 1)

    plt.plot(epochs, runner.train_loss, color='#e4007f', label="Train loss")
    plt.plot(epochs, runner.dev_loss, color='#f19ec2', linestyle='--', label="Dev loss")
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='upper right', fontsize='x-large')

    plt.subplot(1, 2, 2)
    plt.plot(epochs, runner.train_scores, color='#e4007f', label="Train accuracy")
    plt.plot(epochs, runner.dev_scores, color='#f19ec2', linestyle='--', label="Dev accuracy")
    # 绘制坐标轴和图例
    plt.ylabel("score", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='lower right', fontsize='x-large')

    plt.savefig(fig_name)
    plt.show()



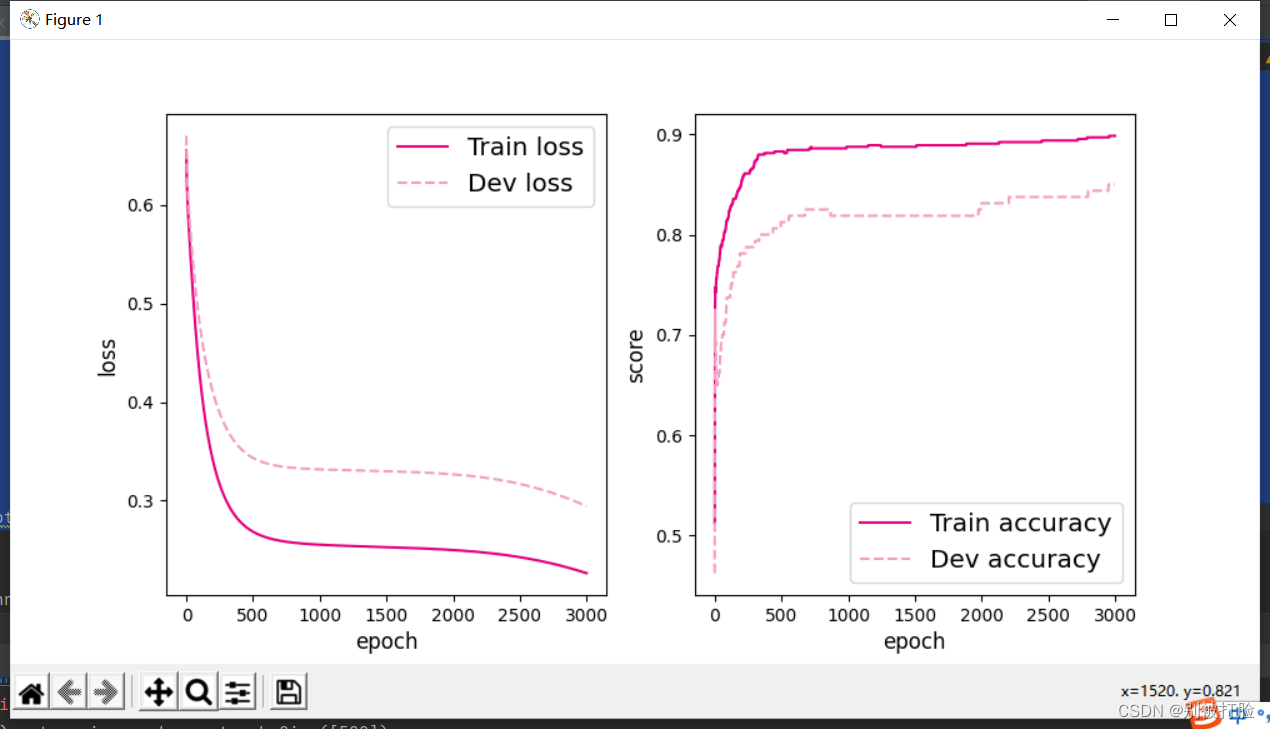
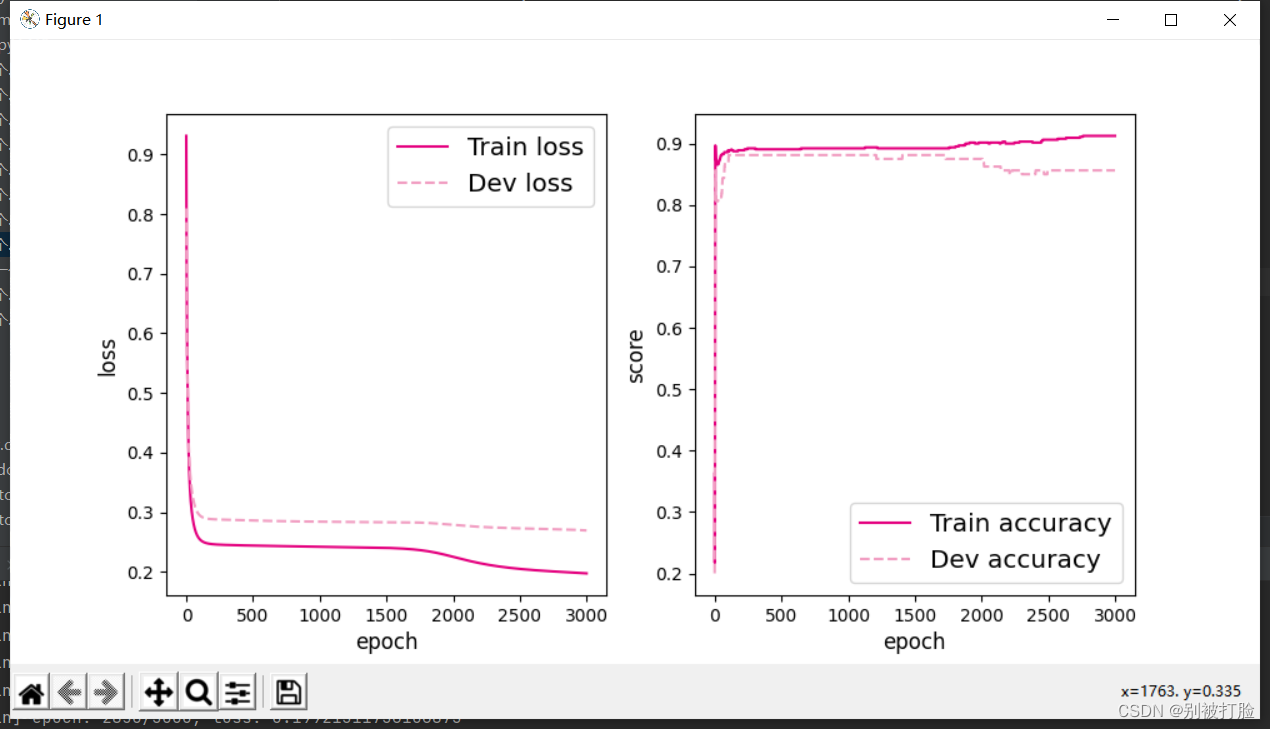
plot(runner, 'fw-acc.pdf')

代码的大致思想：

        这个就是正常的函数调用画图。 

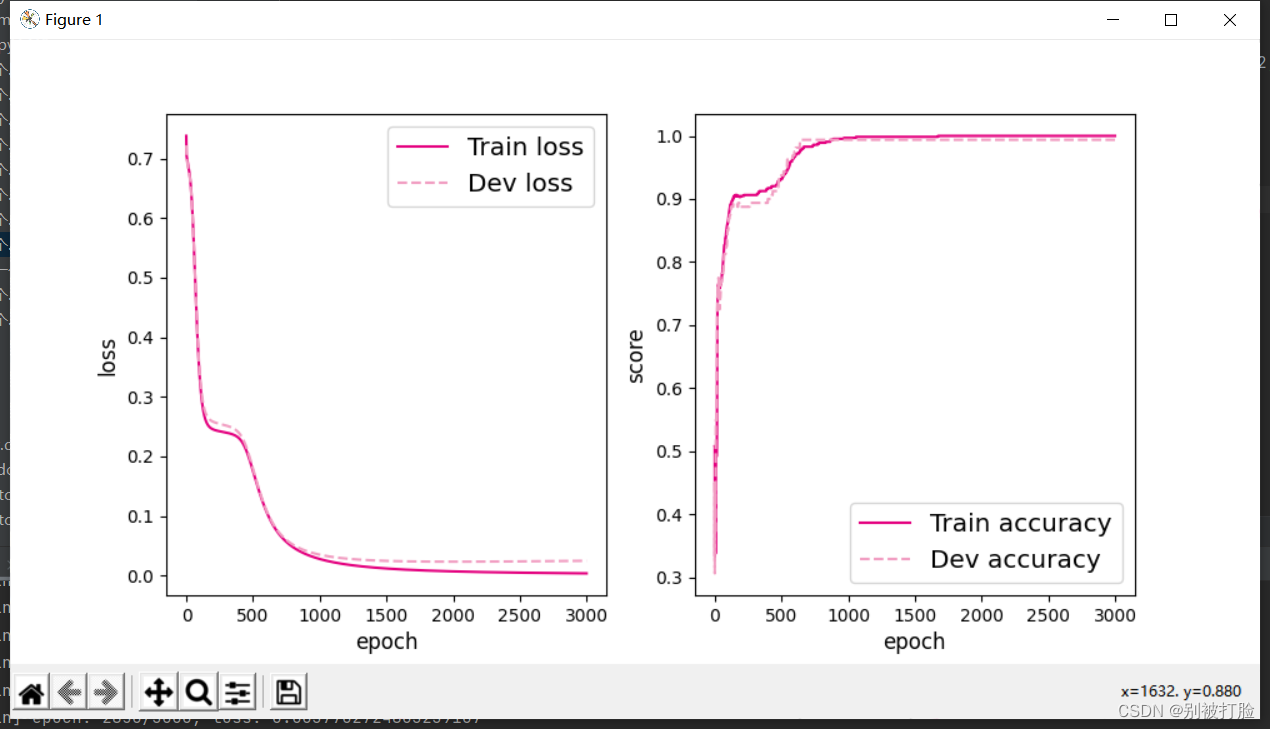
 运行结果为：

  4.3.1.3 性能评价

runner.load_model("best_model.pdparams")
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

运行结果为：

[Test] score/loss: 0.9050/0.2242 

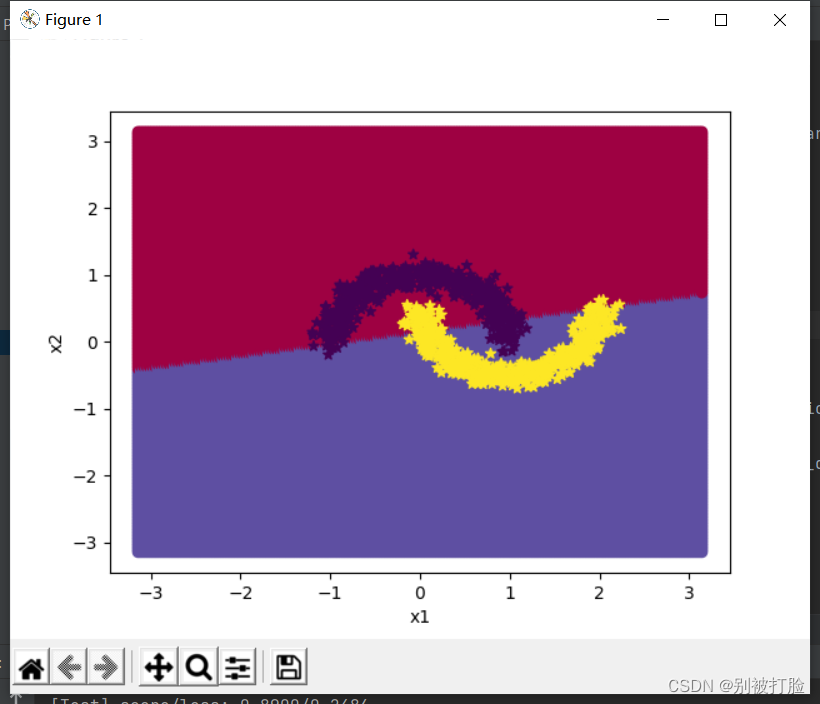
最后我们，画一下图，来表示一下。

# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-math.pi, math.pi, 200), torch.linspace(-math.pi, math.pi, 200))
x = torch.stack([torch.flatten(x1), torch.flatten(x2)], dim=1)

# 预测对应类别
y = runner.predict(x)
y = torch.squeeze(torch.tensor((y>=0.5),dtype=torch.float32),dim=-1)

# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)

plt.scatter(X_train[:, 0].tolist(), X_train[:, 1].tolist(), marker='*', c=torch.squeeze(y_train,dim=-1).tolist())
plt.scatter(X_dev[:, 0].tolist(), X_dev[:, 1].tolist(), marker='*', c=torch.squeeze(y_dev,dim=-1).tolist())
plt.scatter(X_test[:, 0].tolist(), X_test[:, 1].tolist(), marker='*', c=torch.squeeze(y_test,dim=-1).tolist())

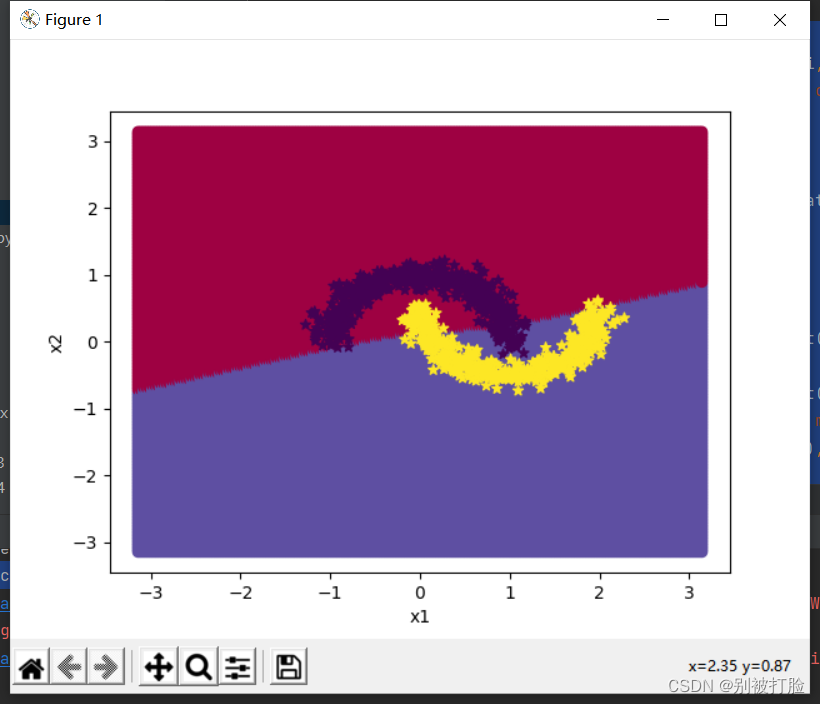
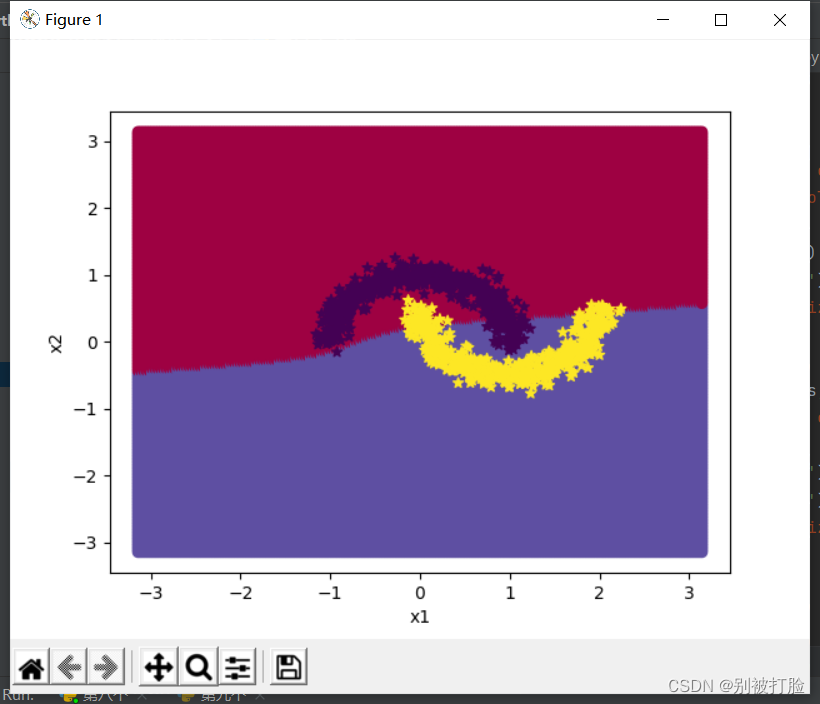
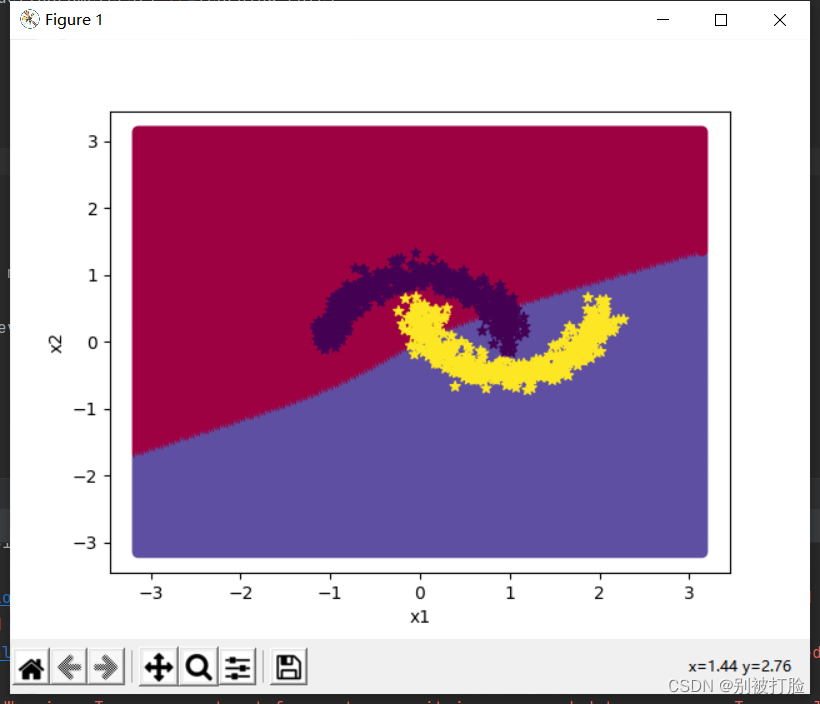
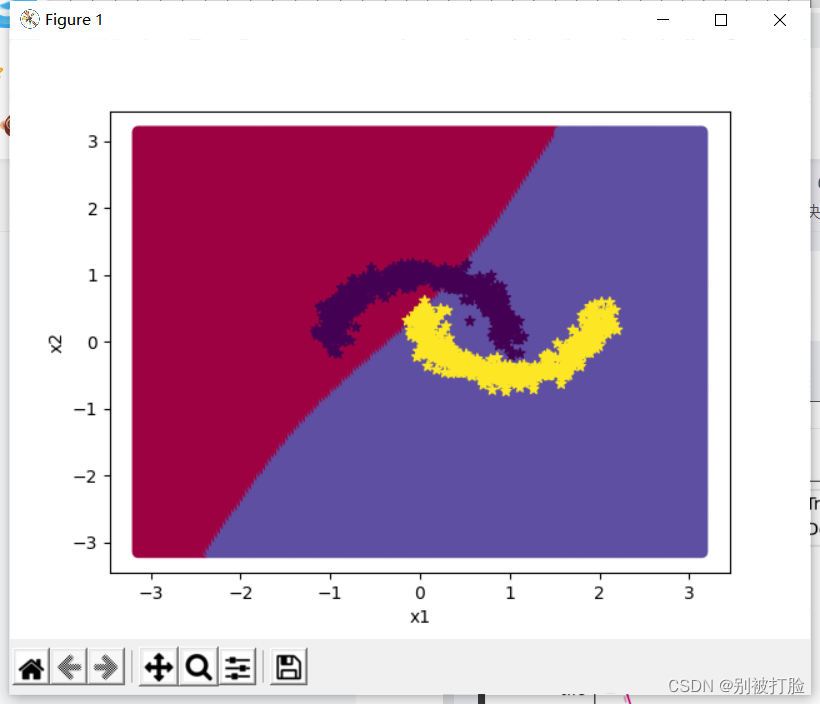
plt.show()

运行的结果为：

这其实说明，现在的超参数还不太好，这留到下边去讨论。 

本题中用到，其他函数或者代码为

# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.1)


num_train = 640
num_dev = 160
num_test = 200

X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])

像其他函数，在我的上一篇博客，当中都有，有兴趣的可以去看一看。

 2. 增加一个3个神经元的隐藏层，再次实现二分类，并与1做对比。（必做）

这个我直接把所有代码，发在一个里边，发便大家观看，上边插开了，是为了逐步逐步的解释一下。

# coding=gbk
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.init import constant_, normal_, uniform_
import torch
from nndl import make_moons
from metric import accuracy
import matplotlib.pyplot as plt
import math

class Model_MLP_L2_V2(nn.Module):
    def __init__(self, input_size, hidden_size1,hidden_size2,output_size):
        super(Model_MLP_L2_V2, self).__init__()
        # 使用'paddle.nn.Linear'定义线性层。
        # 其中第一个参数（in_features）为线性层输入维度；第二个参数（out_features）为线性层输出维度
        # weight_attr为权重参数属性，这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
        # bias_attr为偏置参数属性，这里使用'paddle.nn.initializer.Constant'进行常量初始化
        self.fc1 = nn.Linear(input_size, hidden_size1)
        w1 = torch.empty(hidden_size1,input_size)
        b1=  torch.empty(hidden_size1)
        self.fc1.weight=torch.nn.Parameter(normal_(w1,mean=0.0, std=1.0))
        self.fc1.bias=torch.nn.Parameter(constant_(b1,val=0.0))

        self.fc2 = nn.Linear(hidden_size1, hidden_size2)
        w2 = torch.empty(hidden_size2,hidden_size1)
        b2 = torch.empty(hidden_size2)
        self.fc2.weight=torch.nn.Parameter(normal_(w2,mean=0.0, std=1.0))
        self.fc2.bias=torch.nn.Parameter(constant_(b2,val=0.0))


        self.fc3 = nn.Linear(hidden_size2, output_size)
        w3 = torch.empty(output_size, hidden_size2)
        b3 = torch.empty(output_size)
        self.fc3.weight = torch.nn.Parameter(normal_(w3, mean=0.0, std=1.0))
        self.fc3.bias = torch.nn.Parameter(constant_(b3, val=0.0))

        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = F.sigmoid

    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        z3=self.fc3(a2)
        a3=self.act_fn(z3)
        return a3


class RunnerV2_2(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        # 将模型切换为训练模式
        self.model.train()

        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)
        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")

        # log打印函数，如果没有传入则默认为"None"
        custom_print_log = kwargs.get("custom_print_log", None)

        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)
            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)

            # 自动计算参数梯度
            trn_loss.backward()
            if custom_print_log is not None:
                # 打印每一层的梯度
                custom_print_log(self)

            # 参数更新
            self.optimizer.step()
            # 清空梯度
            self.optimizer.zero_grad()

            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                self.save_model(save_path)
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")

    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def evaluate(self, data_set):
        # 将模型切换为评估模式
        self.model.eval()

        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss

    # 模型测试阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def predict(self, X):
        # 将模型切换为评估模式
        self.model.eval()
        return self.model(X)

    # 使用'model.state_dict()'获取模型参数，并进行保存
    def save_model(self, saved_path):
        torch.save(self.model.state_dict(), saved_path)

    # 使用'model.set_state_dict'加载模型参数
    def load_model(self, model_path):
        state_dict = torch.load(model_path)
        self.model.load_state_dict(state_dict)



# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.1)


num_train = 640
num_dev = 160
num_test = 200

X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])





# 设置模型
input_size = 2
hidden_size1 = 5
hidden_size2=3
output_size = 1
model = Model_MLP_L2_V2(input_size=input_size, hidden_size1=hidden_size1,hidden_size2=hidden_size2, output_size=output_size)

# 设置损失函数
loss_fn = F.binary_cross_entropy

# 设置优化器
learning_rate = 0.2
optimizer = torch.optim.SGD(params=model.parameters(),lr=learning_rate)

# 设置评价指标
metric = accuracy

# 其他参数
epoch_num = 3000
saved_path = "best_model.pdparams"

# 实例化RunnerV2类，并传入训练配置
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_path="best_model.pdparams")


# 可视化观察训练集与验证集的指标变化情况
def plot(runner, fig_name):
    plt.figure(figsize=(10, 5))
    epochs = [i for i in range(0,len(runner.train_scores))]

    plt.subplot(1, 2, 1)

    plt.plot(epochs, runner.train_loss, color='#e4007f', label="Train loss")
    plt.plot(epochs, runner.dev_loss, color='#f19ec2', linestyle='--', label="Dev loss")
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='upper right', fontsize='x-large')

    plt.subplot(1, 2, 2)
    plt.plot(epochs, runner.train_scores, color='#e4007f', label="Train accuracy")
    plt.plot(epochs, runner.dev_scores, color='#f19ec2', linestyle='--', label="Dev accuracy")
    # 绘制坐标轴和图例
    plt.ylabel("score", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='lower right', fontsize='x-large')

    plt.savefig(fig_name)
    plt.show()



plot(runner, 'fw-acc.pdf')


runner.load_model("best_model.pdparams")
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))


# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-math.pi, math.pi, 200), torch.linspace(-math.pi, math.pi, 200))
x = torch.stack([torch.flatten(x1), torch.flatten(x2)], dim=1)

# 预测对应类别
y = runner.predict(x)
y = torch.squeeze(torch.tensor((y>=0.5),dtype=torch.float32),dim=-1)

# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)

plt.scatter(X_train[:, 0].tolist(), X_train[:, 1].tolist(), marker='*', c=torch.squeeze(y_train,dim=-1).tolist())
plt.scatter(X_dev[:, 0].tolist(), X_dev[:, 1].tolist(), marker='*', c=torch.squeeze(y_dev,dim=-1).tolist())
plt.scatter(X_test[:, 0].tolist(), X_test[:, 1].tolist(), marker='*', c=torch.squeeze(y_test,dim=-1).tolist())

plt.show()

       其实更改的地方只有，神经网络的调用那一部分，和相应的传参那一部分。但是为了，看着的一个整体性，所以我写在一个里边。

并且由于一个人们都知道的知识，当神经网络层数越多时，所需要的迭代的次数越多，才能体现优越性。这个是和的调参有关的，我会在下边说，这次先为了对比一下         

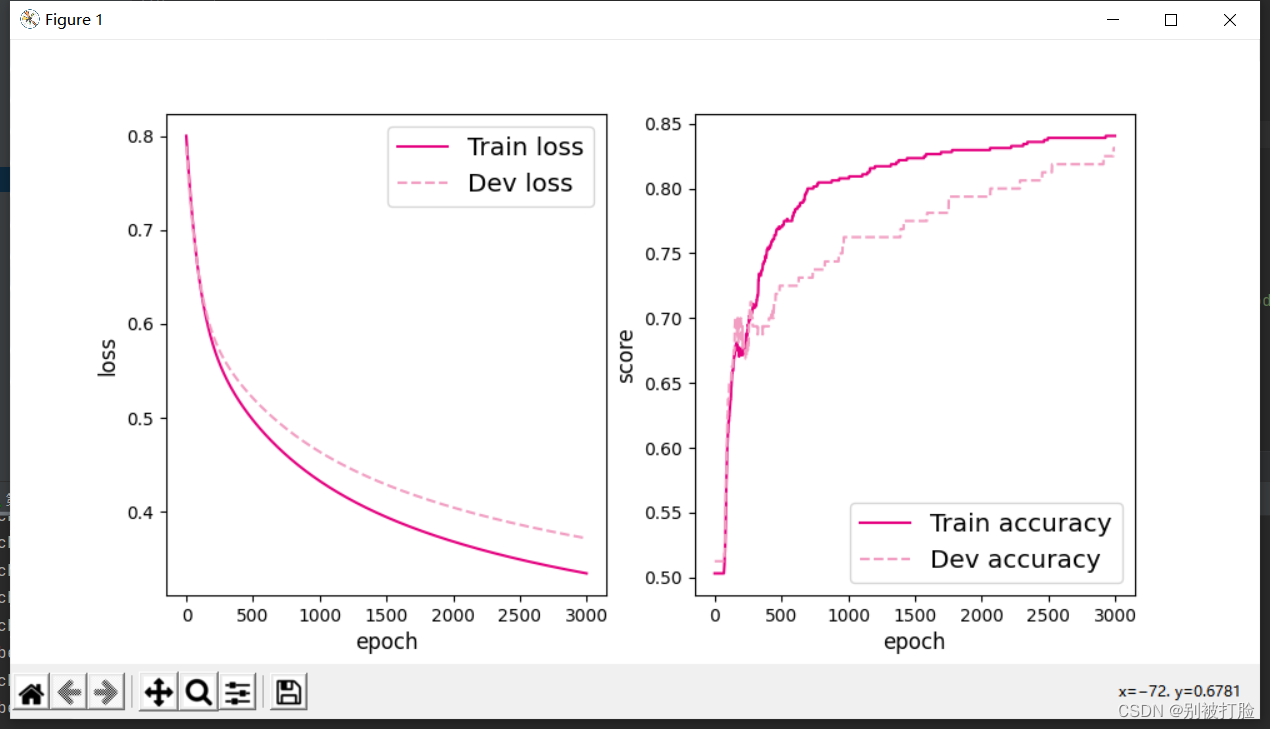
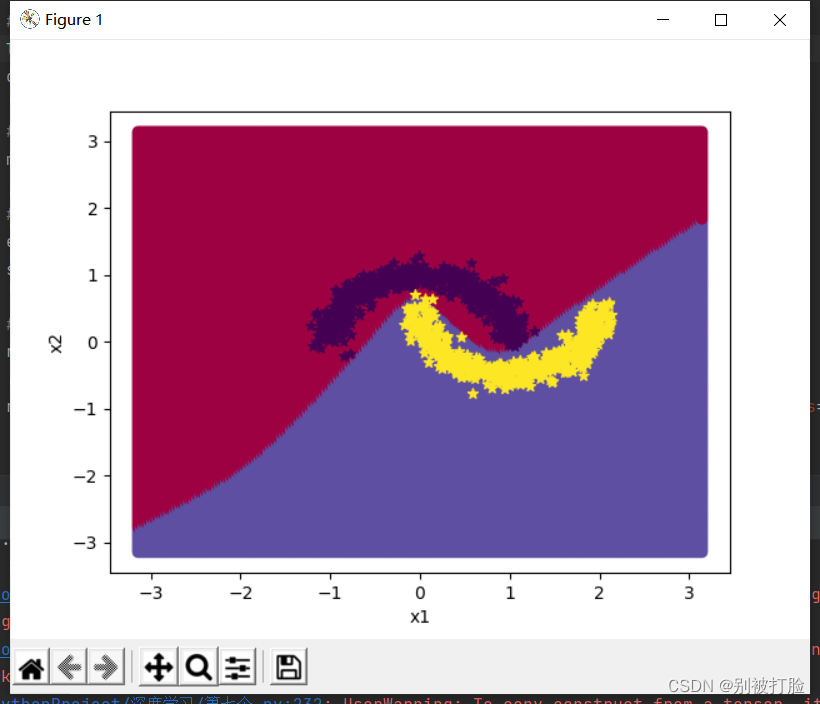
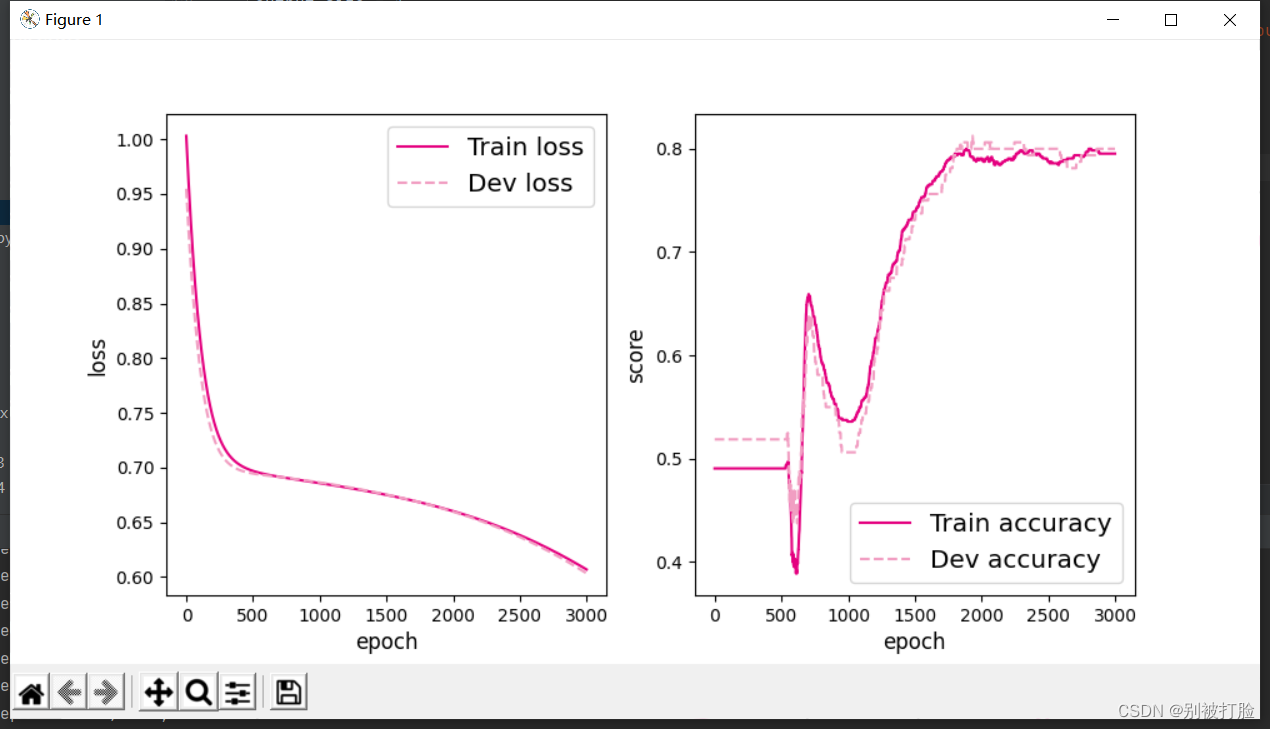
        运行结果为：

epoch=3000时

[Evaluate] best accuracy performence has been updated: 0.00000 –> 0.46250
[Train] epoch: 0/3000, loss: 0.6551498174667358
[Evaluate] best accuracy performence has been updated: 0.46250 –> 0.60625
[Evaluate] best accuracy performence has been updated: 0.60625 –> 0.68750
[Evaluate] best accuracy performence has been updated: 0.68750 –> 0.72500
[Train] epoch: 50/3000, loss: 0.5103745460510254
[Evaluate] best accuracy performence has been updated: 0.72500 –> 0.73125
[Evaluate] best accuracy performence has been updated: 0.73125 –> 0.73750
[Train] epoch: 100/3000, loss: 0.42853039503097534
[Evaluate] best accuracy performence has been updated: 0.73750 –> 0.74375
[Evaluate] best accuracy performence has been updated: 0.74375 –> 0.75000
[Evaluate] best accuracy performence has been updated: 0.75000 –> 0.75625
[Evaluate] best accuracy performence has been updated: 0.75625 –> 0.76250
[Train] epoch: 150/3000, loss: 0.37542006373405457
[Evaluate] best accuracy performence has been updated: 0.76250 –> 0.76875
[Evaluate] best accuracy performence has been updated: 0.76875 –> 0.77500
[Evaluate] best accuracy performence has been updated: 0.77500 –> 0.78125
[Train] epoch: 200/3000, loss: 0.3404920995235443
[Evaluate] best accuracy performence has been updated: 0.78125 –> 0.78750
[Train] epoch: 250/3000, loss: 0.31656843423843384
[Train] epoch: 300/3000, loss: 0.2997353672981262
[Evaluate] best accuracy performence has been updated: 0.78750 –> 0.79375
[Evaluate] best accuracy performence has been updated: 0.79375 –> 0.80000
[Train] epoch: 350/3000, loss: 0.287742555141449
[Train] epoch: 400/3000, loss: 0.2791396677494049
[Evaluate] best accuracy performence has been updated: 0.80000 –> 0.80625
[Train] epoch: 450/3000, loss: 0.2729260325431824
[Evaluate] best accuracy performence has been updated: 0.80625 –> 0.81250
[Train] epoch: 500/3000, loss: 0.26839905977249146
[Train] epoch: 550/3000, loss: 0.2650667428970337
[Evaluate] best accuracy performence has been updated: 0.81250 –> 0.81875
[Train] epoch: 600/3000, loss: 0.2625855803489685
[Train] epoch: 650/3000, loss: 0.26071539521217346
[Evaluate] best accuracy performence has been updated: 0.81875 –> 0.82500
[Train] epoch: 700/3000, loss: 0.2592872381210327
[Train] epoch: 750/3000, loss: 0.2581814229488373
[Train] epoch: 800/3000, loss: 0.25731244683265686
[Train] epoch: 850/3000, loss: 0.25661858916282654
[Train] epoch: 900/3000, loss: 0.25605499744415283
[Train] epoch: 950/3000, loss: 0.25558871030807495
[Train] epoch: 1000/3000, loss: 0.25519540905952454
[Train] epoch: 1050/3000, loss: 0.25485676527023315
[Train] epoch: 1100/3000, loss: 0.25455909967422485
[Train] epoch: 1150/3000, loss: 0.254291832447052
[Train] epoch: 1200/3000, loss: 0.25404682755470276
[Train] epoch: 1250/3000, loss: 0.253817617893219
[Train] epoch: 1300/3000, loss: 0.25359901785850525
[Train] epoch: 1350/3000, loss: 0.25338679552078247
[Train] epoch: 1400/3000, loss: 0.25317731499671936
[Train] epoch: 1450/3000, loss: 0.25296729803085327
[Train] epoch: 1500/3000, loss: 0.2527539134025574
[Train] epoch: 1550/3000, loss: 0.25253432989120483
[Train] epoch: 1600/3000, loss: 0.252305805683136
[Train] epoch: 1650/3000, loss: 0.2520657181739807
[Train] epoch: 1700/3000, loss: 0.25181102752685547
[Train] epoch: 1750/3000, loss: 0.25153887271881104
[Train] epoch: 1800/3000, loss: 0.25124597549438477
[Train] epoch: 1850/3000, loss: 0.25092893838882446
[Train] epoch: 1900/3000, loss: 0.2505839467048645
[Train] epoch: 1950/3000, loss: 0.25020694732666016
[Evaluate] best accuracy performence has been updated: 0.82500 –> 0.83125
[Train] epoch: 2000/3000, loss: 0.2497936487197876
[Train] epoch: 2050/3000, loss: 0.24933934211730957
[Train] epoch: 2100/3000, loss: 0.2488391101360321
[Train] epoch: 2150/3000, loss: 0.2482878416776657
[Train] epoch: 2200/3000, loss: 0.24768006801605225
[Evaluate] best accuracy performence has been updated: 0.83125 –> 0.83750
[Train] epoch: 2250/3000, loss: 0.24701039493083954
[Train] epoch: 2300/3000, loss: 0.24627332389354706
[Train] epoch: 2350/3000, loss: 0.24546349048614502
[Train] epoch: 2400/3000, loss: 0.24457550048828125
[Train] epoch: 2450/3000, loss: 0.24360433220863342
[Train] epoch: 2500/3000, loss: 0.24254508316516876
[Train] epoch: 2550/3000, loss: 0.24139317870140076
[Train] epoch: 2600/3000, loss: 0.2401442527770996
[Train] epoch: 2650/3000, loss: 0.2387942522764206
[Train] epoch: 2700/3000, loss: 0.23733949661254883
[Train] epoch: 2750/3000, loss: 0.23577670753002167
[Evaluate] best accuracy performence has been updated: 0.83750 –> 0.84375
[Train] epoch: 2800/3000, loss: 0.23410315811634064
[Train] epoch: 2850/3000, loss: 0.2323170006275177
[Train] epoch: 2900/3000, loss: 0.23041728138923645
[Evaluate] best accuracy performence has been updated: 0.84375 –> 0.85000
[Train] epoch: 2950/3000, loss: 0.22840432822704315
[Test] score/loss: 0.9050/0.2242

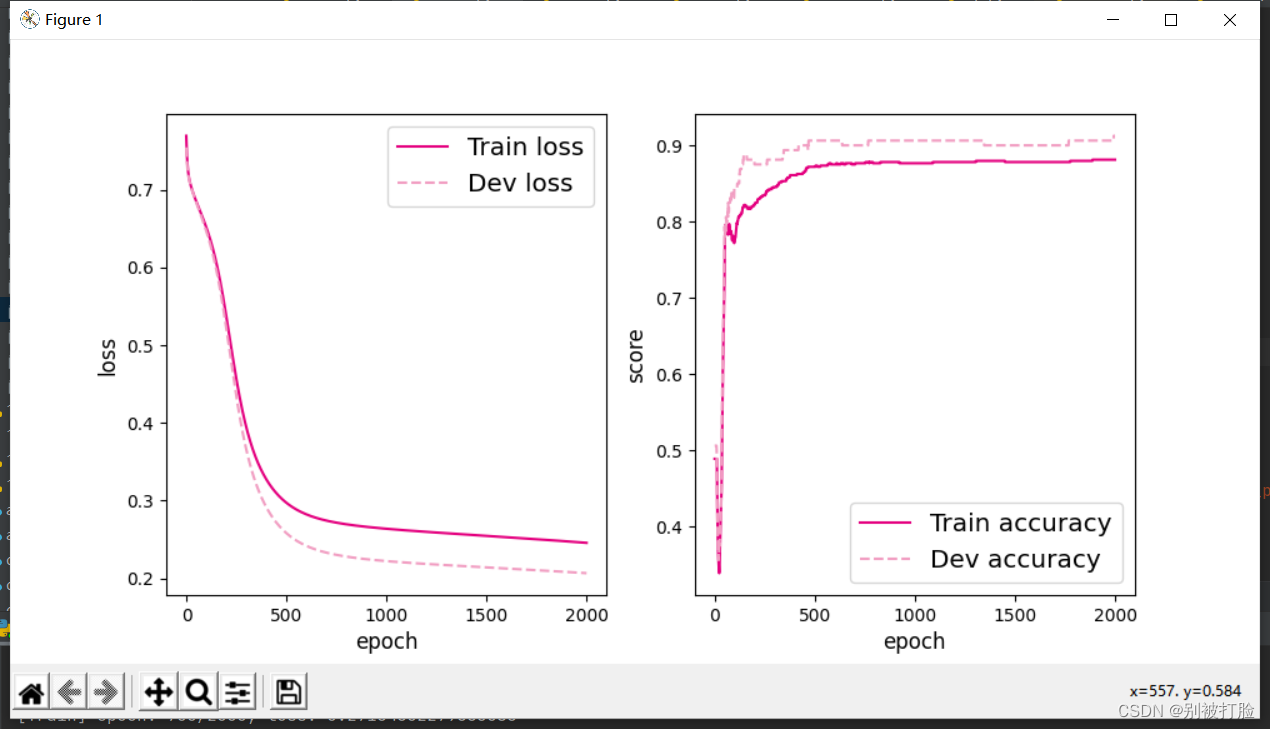
当epoch=2000时 

[Evaluate] best accuracy performence has been updated: 0.00000 –> 0.50625
[Train] epoch: 0/2000, loss: 0.7695772051811218
[Evaluate] best accuracy performence has been updated: 0.50625 –> 0.53750
[Evaluate] best accuracy performence has been updated: 0.53750 –> 0.55625
[Evaluate] best accuracy performence has been updated: 0.55625 –> 0.58125
[Evaluate] best accuracy performence has been updated: 0.58125 –> 0.60625
[Evaluate] best accuracy performence has been updated: 0.60625 –> 0.62500
[Evaluate] best accuracy performence has been updated: 0.62500 –> 0.63750
[Evaluate] best accuracy performence has been updated: 0.63750 –> 0.65000
[Evaluate] best accuracy performence has been updated: 0.65000 –> 0.66875
[Evaluate] best accuracy performence has been updated: 0.66875 –> 0.68125
[Evaluate] best accuracy performence has been updated: 0.68125 –> 0.69375
[Evaluate] best accuracy performence has been updated: 0.69375 –> 0.71250
[Evaluate] best accuracy performence has been updated: 0.71250 –> 0.73125
[Evaluate] best accuracy performence has been updated: 0.73125 –> 0.75000
[Evaluate] best accuracy performence has been updated: 0.75000 –> 0.78125
[Evaluate] best accuracy performence has been updated: 0.78125 –> 0.79375
[Train] epoch: 50/2000, loss: 0.6851401925086975
[Evaluate] best accuracy performence has been updated: 0.79375 –> 0.80000
[Evaluate] best accuracy performence has been updated: 0.80000 –> 0.80625
[Evaluate] best accuracy performence has been updated: 0.80625 –> 0.81250
[Evaluate] best accuracy performence has been updated: 0.81250 –> 0.82500
[Evaluate] best accuracy performence has been updated: 0.82500 –> 0.83125
[Evaluate] best accuracy performence has been updated: 0.83125 –> 0.83750
[Evaluate] best accuracy performence has been updated: 0.83750 –> 0.84375
[Train] epoch: 100/2000, loss: 0.6518415212631226
[Evaluate] best accuracy performence has been updated: 0.84375 –> 0.85000
[Evaluate] best accuracy performence has been updated: 0.85000 –> 0.85625
[Evaluate] best accuracy performence has been updated: 0.85625 –> 0.86250
[Evaluate] best accuracy performence has been updated: 0.86250 –> 0.86875
[Evaluate] best accuracy performence has been updated: 0.86875 –> 0.87500
[Evaluate] best accuracy performence has been updated: 0.87500 –> 0.88125
[Evaluate] best accuracy performence has been updated: 0.88125 –> 0.88750
[Train] epoch: 150/2000, loss: 0.6065284609794617
[Train] epoch: 200/2000, loss: 0.5372008085250854
[Train] epoch: 250/2000, loss: 0.4569132328033447
[Train] epoch: 300/2000, loss: 0.39426156878471375
[Evaluate] best accuracy performence has been updated: 0.88750 –> 0.89375
[Train] epoch: 350/2000, loss: 0.35365113615989685
[Train] epoch: 400/2000, loss: 0.3273332417011261
[Evaluate] best accuracy performence has been updated: 0.89375 –> 0.90000
[Train] epoch: 450/2000, loss: 0.309579461812973
[Evaluate] best accuracy performence has been updated: 0.90000 –> 0.90625
[Train] epoch: 500/2000, loss: 0.29726406931877136
[Train] epoch: 550/2000, loss: 0.2885670065879822
[Train] epoch: 600/2000, loss: 0.28232163190841675
[Train] epoch: 650/2000, loss: 0.2777450382709503
[Train] epoch: 700/2000, loss: 0.2743062973022461
[Train] epoch: 750/2000, loss: 0.27164602279663086
[Train] epoch: 800/2000, loss: 0.2695213258266449
[Train] epoch: 850/2000, loss: 0.2677682042121887
[Train] epoch: 900/2000, loss: 0.266275018453598
[Train] epoch: 950/2000, loss: 0.2649657428264618
[Train] epoch: 1000/2000, loss: 0.26378774642944336
[Train] epoch: 1050/2000, loss: 0.2627045810222626
[Train] epoch: 1100/2000, loss: 0.26169055700302124
[Train] epoch: 1150/2000, loss: 0.26072728633880615
[Train] epoch: 1200/2000, loss: 0.25980144739151
[Train] epoch: 1250/2000, loss: 0.25890326499938965
[Train] epoch: 1300/2000, loss: 0.25802522897720337
[Train] epoch: 1350/2000, loss: 0.2571617066860199
[Train] epoch: 1400/2000, loss: 0.256307989358902
[Train] epoch: 1450/2000, loss: 0.25546035170555115
[Train] epoch: 1500/2000, loss: 0.2546156048774719
[Train] epoch: 1550/2000, loss: 0.25377076864242554
[Train] epoch: 1600/2000, loss: 0.2529231011867523
[Train] epoch: 1650/2000, loss: 0.252069890499115
[Train] epoch: 1700/2000, loss: 0.25120818614959717
[Train] epoch: 1750/2000, loss: 0.25033479928970337
[Train] epoch: 1800/2000, loss: 0.24944618344306946
[Train] epoch: 1850/2000, loss: 0.24853801727294922
[Train] epoch: 1900/2000, loss: 0.2476053237915039
[Train] epoch: 1950/2000, loss: 0.2466421127319336
[Evaluate] best accuracy performence has been updated: 0.90625 –> 0.91250

 

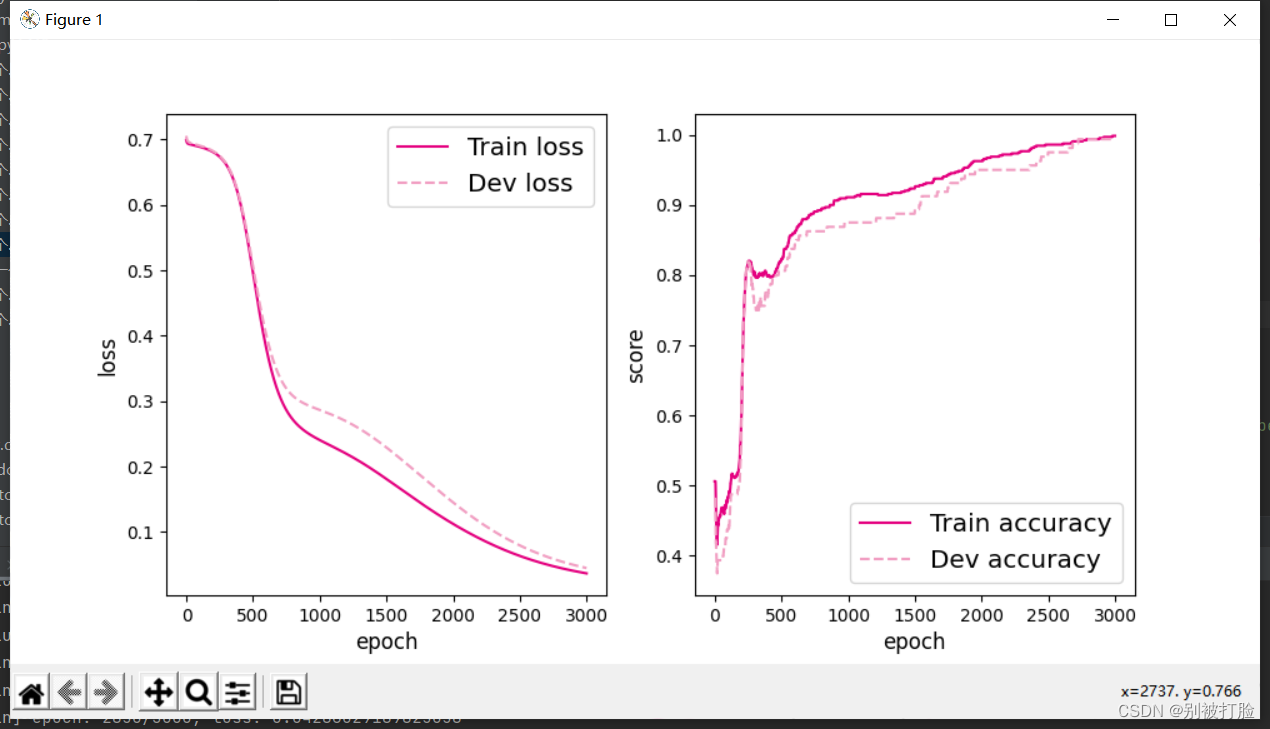
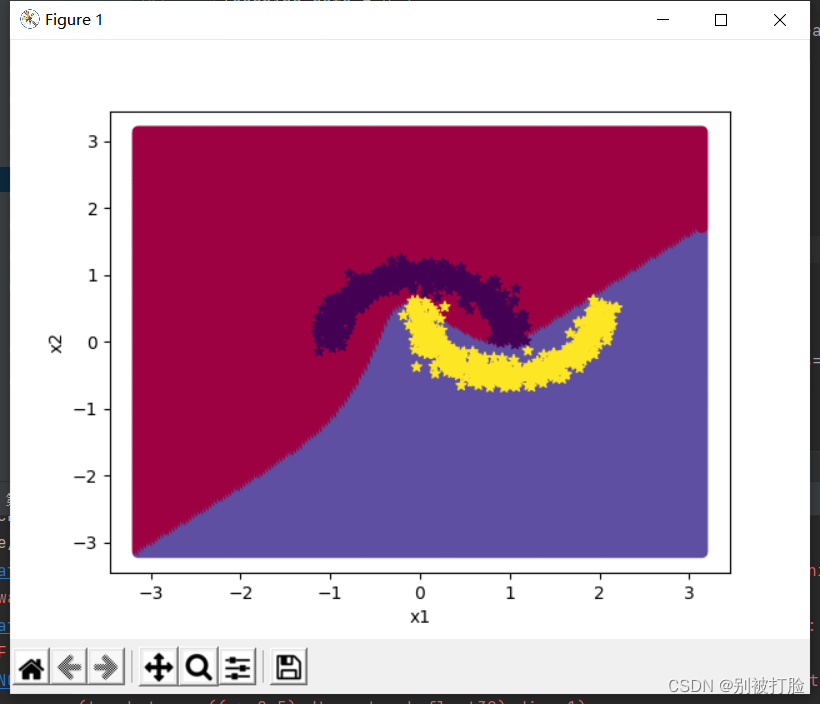
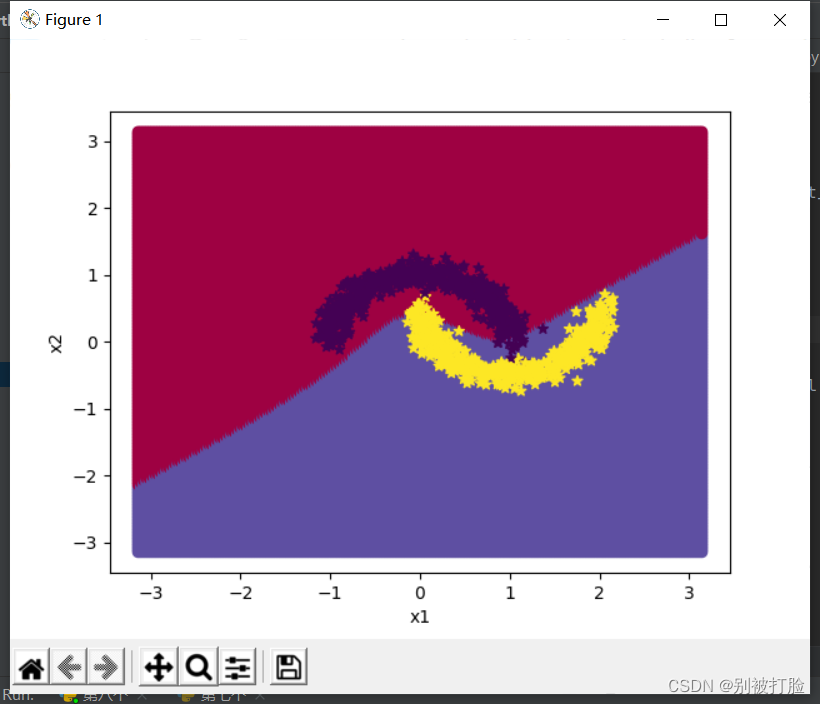
        从最后的图像上就可以直观的看出，当层数较多时，只有足够多的训练次数才能体现出神经网络的优越性。

       说一下层数的选取的问题，和每层选取的节点个数的问题(这个其实上学期，我就问过老师，老师说这个其实是不是固定，也没什么绝对的惯例，但是我感觉有大致的经验是可以借鉴的。）

神经网络主要由输入层，隐藏层以及输出层构成，合理的选择神经网络的层数以及隐藏层神经元的个数，会在很大程度上影响模型的性能（不论是进行分类还是回归任务）。

 输入层的节点数量以及输出层的节点数量是最容易获得的。

输入层的神经元数量等于数据的特征数量（feature个数）。

若为回归，则输出层的神经元数量等于1；若为分类，则输出层的神经元数量为分类的类别个数（如区分猫狗，则为2；区分手写数字0-9，则为10）。

 下边说一个规律

• 没有隐藏层：仅能够表示线性可分函数或决策
• 隐藏层数=1：可以拟合任何“包含从一个有限空间到另一个有限空间的连续映射”的函数
• 隐藏层数=2：搭配适当的激活函数可以表示任意精度的任意决策边界，并且可以拟合任何精度的任何平滑映射
• 隐藏层数>2：多出来的隐藏层可以学习复杂的描述（某种自动特征工程）

也就是下边图的这个意思，当隐层越多，拟合能力越强，但是拟合越复杂，所需要的续联资源越多

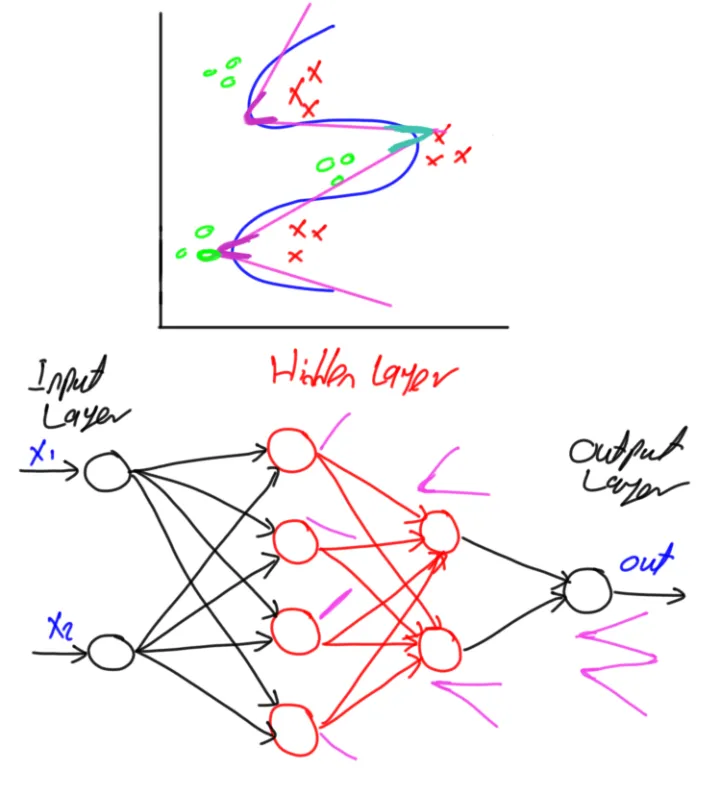
这个是原文，有兴趣的可以去看一看。这篇文章中给出了个数的大致规律

神经元数量通常可以由一下几个原则大致确定：

• 隐藏神经元的数量应在输入层的大小和输出层的大小之间。
• 隐藏神经元的数量应为输入层大小的2/3加上输出层大小的2/3。
• 隐藏神经元的数量应小于输入层大小的两倍。

总而言之，隐藏层神经元是最佳数量需要自己通过不断试验获得，建议从一个较小数值比如1到5层和1到100个神经元开始，如果欠拟合然后慢慢添加更多的层和神经元，如果过拟合就减小层数和神经元。

感觉可以借鉴借鉴，但是我还是觉得老师说的有道理。

3. 自定义隐藏层层数和每个隐藏层中的神经元个数，尝试找到最优超参数完成二分类。可以适当修改数据集，便于探索超参数。（选做）

首先，先说一些，我之前看视频的文档，或者找到资料，或者积累的经验。(个人感觉有点重要）

学习速率(learning rate)。学习速率的设置第一次可以设置大一点的学习率加快收敛，后续慢慢调整；也可以采用动态变化学习速率的方式（比如，每一轮乘以一个衰减系数或者根据损失的变化动态调整学习速率）。

变量初始化(initializer)。常见的变量初始化有零值初始化、随机初始化、均匀分布初始值、正态分布初始值和正交分布初始值。一般采用正态分布或均匀分布的初始化值，有的论文说正交分布的初始值能带来更好的效果。实验的时候可以才正态分布和正交分布初始值做一个尝试。

训练轮数(epoch)。模型收敛即可停止迭代，一般可采用验证集作为停止迭代的条件。如果连续几轮模型损失都没有相应减少，则停止迭代。

优化器。机器学习训练的目的在于更新参数，优化目标函数，常见优化器有SGD，Adagrad，Adadelta，Adam，Adamax，Nadam。其中SGD和Adam优化器是最为常用的两种优化器，SGD根据每个batch的数据计算一次局部的估计，最小化代价函数。
学习速率决定了每次步进的大小，因此我们需要选择一个合适的学习速率进行调优。学习速率太大会导致不收敛，速率太小收敛速度慢。因此SGD通常训练时间更长，但是在好的初始化和学习率调度方案的情况下，结果更可靠。

每轮训练数据乱序(shuffle)。每轮数据迭代保持不同的顺序，避免模型每轮都对相同的数据进行计算。

下边，说完了这些规律直接上实操。

咱们调整网络隐藏层数和学习率的大小，因为上面已经试出了，epoch=3000的时候就比较合适。

首先，隐藏层数为1，学习率为0.01

[Test] score/loss: 0.8750/0.3009

 

隐藏层数为1，学习率为1 

[Test] score/loss: 0.8900/0.2486

 

隐藏层数为1，学习率为5

 [Test] score/loss: 0.9950/0.0278

 

 隐藏层数为2，学习率为0.01

[Test] score/loss: 0.8150/0.6595

 

 隐藏层数为2，学习率为1

[Test] score/loss: 0.9650/0.1159，

  隐藏层数为2，学习率为5

[Test] score/loss: 0.9950/0.0278

 

    通过上边的对比可知，在不同情况下，最优的超参数都是不同的，在1层时，最优的为epoch=3000，lr=5，在2层时，最优的为epoch=3000，lr=1。

    问题：

    但是发现2层时，lr=5的时候，能到几乎100%，这个正确率吓人，虽然之前证明了不是过拟合，但是还是感觉不太对劲。

自定义梯度计算和自动梯度计算：从计算性能、计算结果等多方面比较，谈谈自己的看法。

     首先，先说一下我的理解，也就是老师上课讲的，这我们自定义的不仅计算复杂(因为所有的的求导计算，都是由数值微分近似的，这是计算机的特性)，再转化为计算机程序时十分复杂，非常琐碎容易出错。这会导致神经网络的实现变得十分低效。所以从各个方面来说都是自动梯度计算较好。

       下边咱们看一看这学期学的神书，蒲公英书上的。

 然后咱们从具体的例子看一下。

先理解一下，自动梯度含义

这是鱼书给出的解释

 下边咱们看一看这学期学的神书，蒲公英书上的。

理解了定义之后，咱们从实例上来看一下，

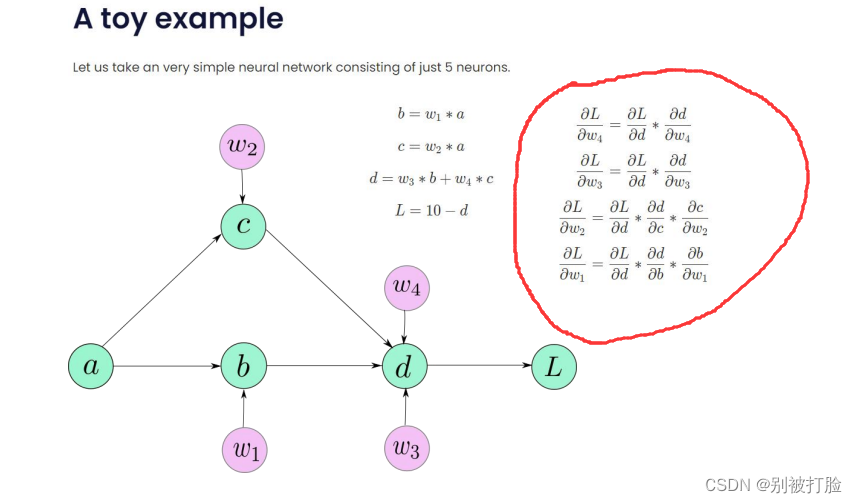
 从上边可以看出，如果是自己定义的求导方式是十分复杂的，这么复杂的式子，这么复杂的计算又耗费时间，又极易出错。

 下边看一看，自动微分求导的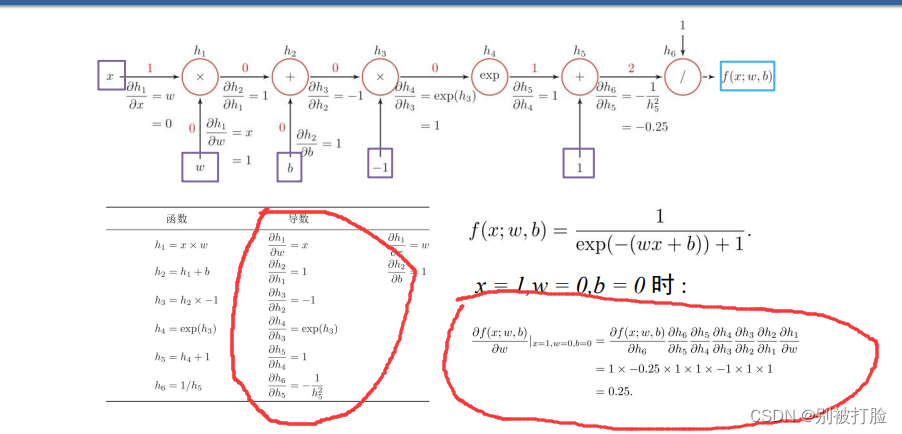

        可以看出，首先，每个单个的导数都非常容易求，并且，就算是连起来也不用像以前一样，求那么长的了，只需每个简单的相乘即可。

       不管是从精度上，从计算时间上，还是计算的复杂度上，还是代码实现的难易程度上，自动微分求导的优越性都是十分明显的。

        另外，我想说的是，咱们是初学阶段，并且时代是不断进步的，是不断发展的，是不断朝着好的方向走的，所以咱们学的肯定是越来越好，所以自动微分求导一定是优于自定义的。

二、4.4 优化问题

  4.4.1 参数初始化

实现一个神经网络前，需要先初始化模型参数。

如果对每一层的权重和偏置都用0初始化，那么通过第一遍前向计算，所有隐藏层神经元的激活值都相同；在反向传播时，所有权重的更新也都相同，这样会导致隐藏层神经元没有差异性，出现对称权重现象。

# coding=gbk
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.init import constant_, normal_, uniform_
import torch
from nndl import make_moons
from metric import accuracy
import matplotlib.pyplot as plt
import math

和上边说的一样，注意解码方式即可。

class Model_MLP_L2_V4(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V4, self).__init__()
        # 使用'paddle.nn.Linear'定义线性层。
        # 其中第一个参数（in_features）为线性层输入维度；第二个参数（out_features）为线性层输出维度
        # weight_attr为权重参数属性，这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
        # bias_attr为偏置参数属性，这里使用'paddle.nn.initializer.Constant'进行常量初始化
        self.fc1 = nn.Linear(input_size, hidden_size)
        w1 = torch.empty(hidden_size,input_size)
        b1=  torch.empty(hidden_size)
        self.fc1.weight=torch.nn.Parameter(constant_(w1,val=0.0))
        self.fc1.bias=torch.nn.Parameter(constant_(b1,val=0.0))
        self.fc2 = nn.Linear(hidden_size, output_size)
        w2 = torch.empty(output_size,hidden_size)
        b2 = torch.empty(output_size)
        self.fc2.weight=torch.nn.Parameter(constant_(w2,val=0.0))
        self.fc2.bias=torch.nn.Parameter(constant_(b2,val=0.0))
        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = F.sigmoid

    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        return a2

接下来，将模型参数全都初始化为0，看实验结果。这里重新定义了一个类TwoLayerNet_Zeros，两个线性层的参数全都初始化为0。

 下边是画图的函数

def print_weights(runner):
    print('The weights of the Layers：')

    for a,item in enumerate(runner.model.named_parameters()):
        print(item)
        print('---------------------------------')

利用Runner类训练模型(Runner函数和上边的是一样的)： 

# 设置模型
input_size = 2
hidden_size = 5
output_size = 1
model = Model_MLP_L2_V4(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 设置损失函数
loss_fn = F.binary_cross_entropy

# 设置优化器
learning_rate = 0.2 #5e-2
optimizer = torch.optim.SGD(params=model.parameters(),lr=learning_rate)

# 设置评价指标
metric = accuracy

# 其他参数
epoch = 2000
saved_path = 'best_model.pdparams'

# 实例化RunnerV2类，并传入训练配置
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=5, log_epochs=50, save_path="best_model.pdparams",custom_print_log=print_weights)

 The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.]], requires_grad=True))
———————————
('fc1.bias', Parameter containing:
tensor([0., 0., 0., 0., 0.], requires_grad=True))
———————————
('fc2.weight', Parameter containing:
tensor([[0., 0., 0., 0., 0.]], requires_grad=True))
———————————
('fc2.bias', Parameter containing:
tensor([0.], requires_grad=True))
———————————
[Evaluate] best accuracy performence has been updated: 0.00000 –> 0.51250
[Train] epoch: 0/5, loss: 0.6931473016738892
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.]], requires_grad=True))
———————————
('fc1.bias', Parameter containing:
tensor([0., 0., 0., 0., 0.], requires_grad=True))
———————————
('fc2.weight', Parameter containing:
tensor([[0.0009, 0.0009, 0.0009, 0.0009, 0.0009]], requires_grad=True))
———————————
('fc2.bias', Parameter containing:
tensor([0.0019], requires_grad=True))
———————————
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[ 1.2101e-05, -9.0942e-06],
        [ 1.2101e-05, -9.0942e-06],
        [ 1.2101e-05, -9.0942e-06],
        [ 1.2101e-05, -9.0942e-06],
        [ 1.2101e-05, -9.0942e-06]], requires_grad=True))
———————————
('fc1.bias', Parameter containing:
tensor([3.9001e-07, 3.9001e-07, 3.9001e-07, 3.9001e-07, 3.9001e-07],
       requires_grad=True))
———————————
('fc2.weight', Parameter containing:
tensor([[0.0018, 0.0018, 0.0018, 0.0018, 0.0018]], requires_grad=True))
———————————
('fc2.bias', Parameter containing:
tensor([0.0035], requires_grad=True))
———————————
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[ 3.4898e-05, -2.6278e-05],
        [ 3.4898e-05, -2.6278e-05],
        [ 3.4898e-05, -2.6278e-05],
        [ 3.4898e-05, -2.6278e-05],
        [ 3.4898e-05, -2.6278e-05]], requires_grad=True))
———————————
('fc1.bias', Parameter containing:
tensor([1.0434e-06, 1.0434e-06, 1.0434e-06, 1.0434e-06, 1.0434e-06],
       requires_grad=True))
———————————
('fc2.weight', Parameter containing:
tensor([[0.0025, 0.0025, 0.0025, 0.0025, 0.0025]], requires_grad=True))
———————————
('fc2.bias', Parameter containing:
tensor([0.0050], requires_grad=True))
———————————
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[ 6.7158e-05, -5.0660e-05],
        [ 6.7158e-05, -5.0660e-05],
        [ 6.7158e-05, -5.0660e-05],
        [ 6.7158e-05, -5.0660e-05],
        [ 6.7158e-05, -5.0660e-05]], requires_grad=True))
———————————
('fc1.bias', Parameter containing:
tensor([1.8652e-06, 1.8652e-06, 1.8652e-06, 1.8652e-06, 1.8652e-06],
       requires_grad=True))
———————————
('fc2.weight', Parameter containing:
tensor([[0.0032, 0.0032, 0.0032, 0.0032, 0.0032]], requires_grad=True))
———————————
('fc2.bias', Parameter containing:
tensor([0.0063], requires_grad=True))
———————————

从上边可以看出，所有权重的更新都相同，即出现了对称权重现象

可视化训练和验证集上的主准确率和loss变化：

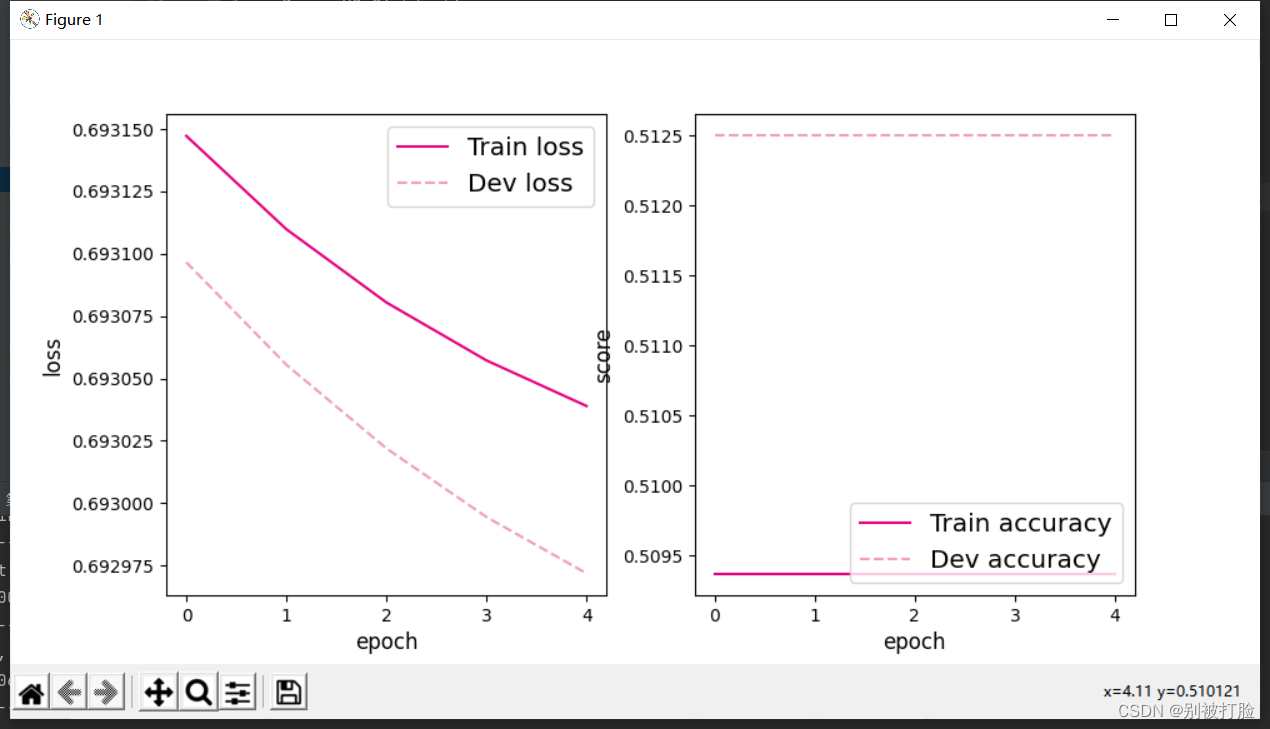
plot(runner, "fw-zero.pdf")

运行结果为：

从输出结果看，二分类准确率为50%左右，说明模型没有学到任何内容。训练和验证loss几乎没有怎么下降。

为了避免对称权重现象，可以使用高斯分布或均匀分布初始化神经网络的参数。

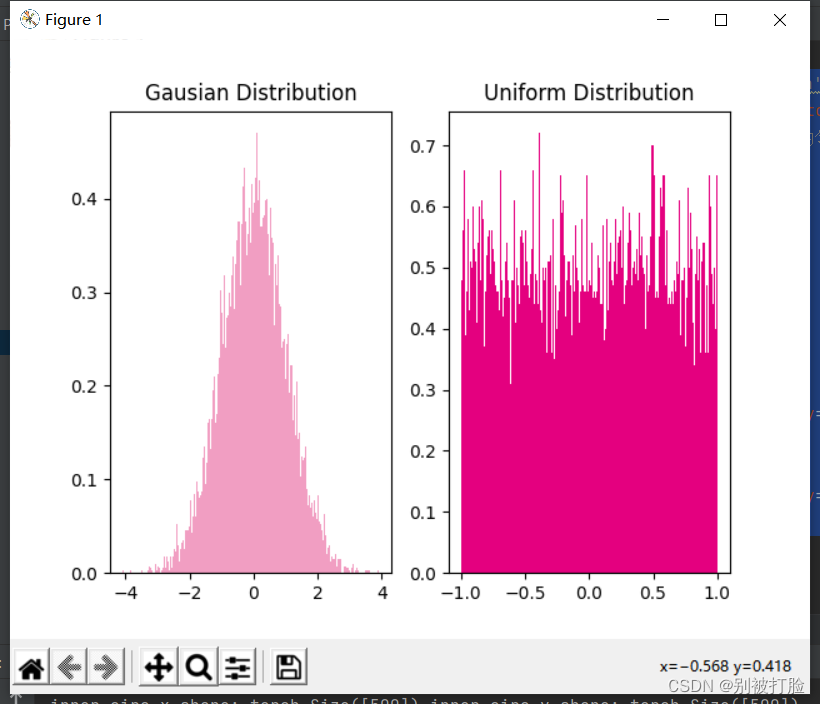
高斯分布和均匀分布采样的实现和可视化代码如下：

# 使用'paddle.normal'实现高斯分布采样，其中'mean'为高斯分布的均值，'std'为高斯分布的标准差，'shape'为输出形状
gausian_weights = torch.normal(mean=0.0, std=1.0, size=[10000])
# 使用'paddle.uniform'实现在[min,max)范围内的均匀分布采样，其中'shape'为输出形状
uniform_weights = torch.Tensor(10000)
uniform_weights.uniform_(-1,1)
gausian_weights=gausian_weights.numpy()
uniform_weights=uniform_weights.numpy()
print(uniform_weights)
# 绘制两种参数分布
plt.figure()
plt.subplot(1,2,1)
plt.title('Gausian Distribution')
plt.hist(gausian_weights, bins=200, density=True, color='#f19ec2')
plt.subplot(1,2,2)
plt.title('Uniform Distribution')
plt.hist(uniform_weights, bins=200, density=True, color='#e4007f')
plt.savefig('fw-gausian-uniform.pdf')
plt.show()

 运行结果为：

  4.4.2 梯度消失问题 

在神经网络的构建过程中，随着网络层数的增加，理论上网络的拟合能力也应该是越来越好的。但是随着网络变深，参数学习更加困难，容易出现梯度消失问题。

由于Sigmoid型函数的饱和性，饱和区的导数更接近于0，误差经过每一层传递都会不断衰减。当网络层数很深时，梯度就会不停衰减，甚至消失，使得整个网络很难训练，这就是所谓的梯度消失问题。
在深度神经网络中，减轻梯度消失问题的方法有很多种，一种简单有效的方式就是使用导数比较大的激活函数，如：ReLU。

4.4.2.1 模型构建

首先，我对输入的参数做了适量的修改，我感觉，这样更好。

class Model_MLP_L5(torch.nn.Module):
    def __init__(self, input_size, output_size, act='sigmoid'):
        super(Model_MLP_L5, self).__init__()
        self.fc1 = torch.nn.Linear(input_size, 3)
        normal_(self.fc1.weight,mean=0.0, std=0.01)
        constant_(self.fc1.bias,val=1.0)
        self.fc2 = torch.nn.Linear(3, 3)
        normal_(self.fc2.weight,mean=0.0, std=0.01)
        constant_(self.fc2.bias,val=1.0)
        self.fc3 = torch.nn.Linear(3, 3)
        normal_(self.fc3.weight,mean=0.0, std=0.01)
        constant_(self.fc3.bias,val=1.0)
        self.fc4 = torch.nn.Linear(3, 3)
        normal_(self.fc4.weight,mean=0.0, std=0.01)
        constant_(self.fc4.bias,val=1.0)
        self.fc5 = torch.nn.Linear(3, output_size)
        normal_(self.fc5.weight,mean=0.0, std=0.01)
        constant_(self.fc5.bias,val=1.0)
        # 定义网络使用的激活函数
        if act == 'sigmoid':
            self.act = F.sigmoid
        elif act == 'relu':
            self.act = F.relu
        elif act == 'lrelu':
            self.act = F.leaky_relu
        else:
            raise ValueError("Please enter sigmoid relu or lrelu!")
    # 初始化线性层权重和偏置参数
    def init_weights(self, w_init, b_init):
        # 使用'named_sublayers'遍历所有网络层
        for n, m in self.named_sublayers():
            # 如果是线性层，则使用指定方式进行参数初始化
            if isinstance(m, nn.Linear):
                w_init(m.weight)
                b_init(m.bias)

    def forward(self, inputs):
        outputs = self.fc1(inputs)
        outputs = self.act(outputs)
        outputs = self.fc2(outputs)
        outputs = self.act(outputs)
        outputs = self.fc3(outputs)
        outputs = self.act(outputs)
        outputs = self.fc4(outputs)
        outputs = self.act(outputs)
        outputs = self.fc5(outputs)
        outputs = F.sigmoid(outputs)
        return outputs

4.4.2.2 使用Sigmoid型函数进行训练

使用Sigmoid型函数作为激活函数，为了便于观察梯度消失现象，只进行一轮网络优化。代码实现如下：

定义梯度打印函数

def print_grads(runner):
    print('The weights of the Layers：')
    for a,item in runner.model.named_parameters():
        print('-->name:', a,' -->grad_value:', item.grad)
        print('---------------------------------')

paddle.seed(102)
# 学习率大小
lr = 0.01

# 定义网络，激活函数使用sigmoid
model =  Model_MLP_L5(input_size=2, output_size=1, act='sigmoid')

# 定义优化器
optimizer = paddle.optimizer.SGD(learning_rate=lr, parameters=model.parameters())

# 定义损失函数，使用交叉熵损失函数
loss_fn = F.binary_cross_entropy

# 定义评价指标
metric = accuracy

# 指定梯度打印函数
custom_print_log=print_grads

实例化RunnerV2_2类，并传入训练配置。代码实现如下：

# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

模型训练，打印网络每层梯度值的L2范数。代码实现如下：

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev],
            num_epochs=1, log_epochs=None,
            save_path="best_model.pdparams",
            custom_print_log=custom_print_log)

运行结果为：

The weights of the Layers：
–>name: fc1.weight  –>grad_value: tensor([[-4.6100e-12,  8.4193e-12],
        [ 3.5136e-12, -6.4185e-12],
        [ 6.2183e-12, -1.1340e-11]])
———————————
–>name: fc1.bias  –>grad_value: tensor([ 7.7229e-12, -5.9049e-12, -1.0396e-11])
———————————
–>name: fc2.weight  –>grad_value: tensor([[1.0906e-09, 1.0889e-09, 1.0918e-09],
        [1.6517e-09, 1.6490e-09, 1.6534e-09],
        [3.9162e-10, 3.9099e-10, 3.9204e-10]])
———————————
–>name: fc2.bias  –>grad_value: tensor([1.4933e-09, 2.2615e-09, 5.3622e-10])
———————————
–>name: fc3.weight  –>grad_value: tensor([[-1.3248e-06, -1.3250e-06, -1.3161e-06],
        [-1.5706e-06, -1.5707e-06, -1.5602e-06],
        [ 1.5241e-06,  1.5243e-06,  1.5141e-06]])
———————————
–>name: fc3.bias  –>grad_value: tensor([-1.8144e-06, -2.1510e-06,  2.0874e-06])
———————————
–>name: fc4.weight  –>grad_value: tensor([[-8.9612e-05, -8.9865e-05, -8.9891e-05],
        [ 6.6466e-04,  6.6653e-04,  6.6672e-04],
        [ 3.7507e-04,  3.7613e-04,  3.7624e-04]])
———————————
–>name: fc4.bias  –>grad_value: tensor([-0.0001,  0.0009,  0.0005])
———————————
–>name: fc5.weight  –>grad_value: tensor([[0.1668, 0.1670, 0.1673]])
———————————
–>name: fc5.bias  –>grad_value: tensor([0.2289])
———————————
[Evaluate] best accuracy performence has been updated: 0.00000 –> 0.47500 

       结果可以看出，结果的小数位数，好多都达到了十几位，也就是几乎更新为0，也就是几乎没有更新权重，也就是几乎没有变化，迭代的非常慢

4.4.2.3 使用ReLU函数进行模型训练

torch.manual_seed(102)
# 学习率大小
lr = 0.01

# 定义网络，激活函数使用sigmoid
model =  Model_MLP_L5(input_size=2, output_size=1, act='relu')

# 定义优化器
optimizer = torch.optim.SGD(params=model.parameters(),lr=lr)

# 定义损失函数，使用交叉熵损失函数
loss_fn = F.binary_cross_entropy

# 定义评价指标
metric = accuracy

# 指定梯度打印函数
custom_print_log=print_grads

# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev],
            num_epochs=1, log_epochs=None,
            save_path="best_model.pdparams",
            custom_print_log=custom_print_log)

运行结果为：

The weights of the Layers：
–>name: fc1.weight  –>grad_value: tensor([[-3.1469e-09,  5.7789e-09],
        [ 2.3632e-09, -4.3397e-09],
        [ 4.2152e-09, -7.7408e-09]])
———————————
–>name: fc1.bias  –>grad_value: tensor([ 5.4743e-09, -4.1109e-09, -7.3327e-09])
———————————
–>name: fc2.weight  –>grad_value: tensor([[2.0650e-07, 2.0531e-07, 2.0730e-07],
        [3.1309e-07, 3.1128e-07, 3.1431e-07],
        [7.2155e-08, 7.1738e-08, 7.2435e-08]])
———————————
–>name: fc2.bias  –>grad_value: tensor([2.0724e-07, 3.1421e-07, 7.2412e-08])
———————————
–>name: fc3.weight  –>grad_value: tensor([[-4.9179e-05, -4.9205e-05, -4.7541e-05],
        [-5.8504e-05, -5.8534e-05, -5.6555e-05],
        [ 5.6837e-05,  5.6867e-05,  5.4944e-05]])
———————————
–>name: fc3.bias  –>grad_value: tensor([-4.9489e-05, -5.8873e-05,  5.7195e-05])
———————————
–>name: fc4.weight  –>grad_value: tensor([[-0.0007, -0.0007, -0.0007],
        [ 0.0048,  0.0049,  0.0049],
        [ 0.0027,  0.0028,  0.0028]])
———————————
–>name: fc4.bias  –>grad_value: tensor([-0.0007,  0.0049,  0.0028])
———————————
–>name: fc5.weight  –>grad_value: tensor([[0.2388, 0.2400, 0.2427]])
———————————
–>name: fc5.bias  –>grad_value: tensor([0.2429])
———————————
[Evaluate] best accuracy performence has been updated: 0.00000 –> 0.52500

        可以认为这个现象与激活函数的使用有一定的关系，结果可以看出，结果的小数位数，好多都达到了十几位，也就是几乎更新为0，也就是几乎没有更新权重，也就是几乎没有变化，迭代的非常慢

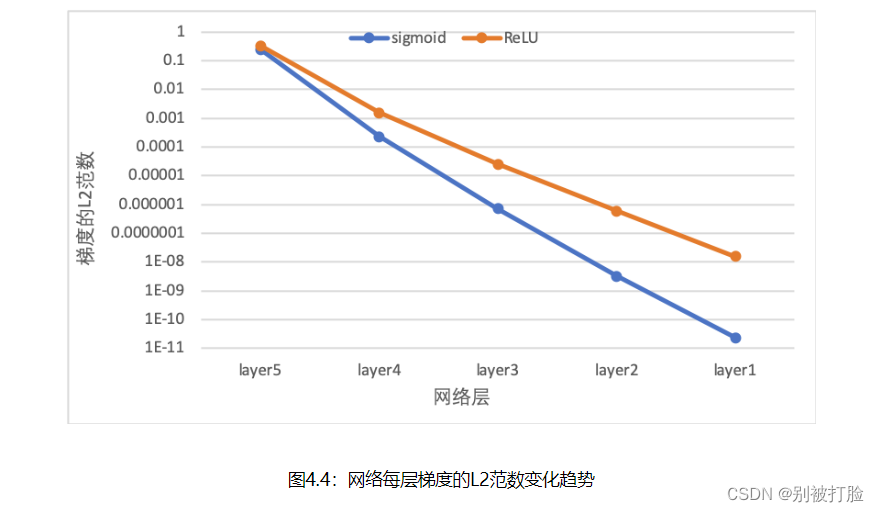
        图4.4   展示了使用不同激活函数时，网络每层梯度值的ℓ2ℓ2范数情况。从结果可以看到，5层的全连接前馈神经网络使用Sigmoid型函数作为激活函数时，梯度经过每一个神经层的传递都会不断衰减，最终传递到第一个神经层时，梯度几乎完全消失。改为ReLU激活函数后，梯度消失现象得到了缓解，每一层的参数都具有梯度值。

 4.4.3 死亡ReLU问题 

         ReLU激活函数可以一定程度上改善梯度消失问题，但是ReLU函数在某些情况下容易出现死亡 ReLU问题，使得网络难以训练。这是由于当x<0x<0时，ReLU函数的输出恒为0。在训练过程中，如果参数在一次不恰当的更新后，某个ReLU神经元在所有训练数据上都不能被激活（即输出为0），那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远都不能被激活。而一种简单有效的优化方式就是将激活函数更换为Leaky ReLU、ELU等ReLU的变种。

4.4.3.1 使用ReLU进行模型训练 

        使用第4.4.2节中定义的多层全连接前馈网络进行实验，使用ReLU作为激活函数，观察死亡ReLU现象和优化方法。当神经层的偏置被初始化为一个相对于权重较大的负值时，可以想像，输入经过神经层的处理，最终的输出会为负值，从而导致死亡ReLU现象。

# 定义网络，并使用较大的负值来初始化偏置
model =  Model_MLP_L5(input_size=2, output_size=1, act='relu')

由于上一问改了一点参数，所以这一问一样也要改一点。 

# 定义多层前馈神经网络
class Model_MLP_L5(torch.nn.Module):
    def __init__(self, input_size, output_size, act='sigmoid'):
        super(Model_MLP_L5, self).__init__()
        self.fc1 = torch.nn.Linear(input_size, 3)
        normal_(self.fc1.weight,mean=0.0, std=0.01)
        constant_(self.fc1.bias,val=-8.0)
        self.fc2 = torch.nn.Linear(3, 3)
        normal_(self.fc2.weight,mean=0.0, std=0.01)
        constant_(self.fc2.bias,val=-8.0)
        self.fc3 = torch.nn.Linear(3, 3)
        normal_(self.fc3.weight,mean=0.0, std=0.01)
        constant_(self.fc3.bias,val=-8.0)
        self.fc4 = torch.nn.Linear(3, 3)
        normal_(self.fc4.weight,mean=0.0, std=0.01)
        constant_(self.fc4.bias,val=-8.0)
        self.fc5 = torch.nn.Linear(3, output_size)
        normal_(self.fc5.weight,mean=0.0, std=0.01)
        constant_(self.fc5.bias,val=-8.0)
        # 定义网络使用的激活函数
        if act == 'sigmoid':
            self.act = F.sigmoid
        elif act == 'relu':
            self.act = F.relu
        elif act == 'lrelu':
            self.act = F.leaky_relu
        else:
            raise ValueError("Please enter sigmoid relu or lrelu!")
    # 初始化线性层权重和偏置参数
    def init_weights(self, w_init, b_init):
        # 使用'named_sublayers'遍历所有网络层
        for n, m in self.named_sublayers():
            # 如果是线性层，则使用指定方式进行参数初始化
            if isinstance(m, nn.Linear):
                w_init(m.weight)
                b_init(m.bias)

    def forward(self, inputs):
        outputs = self.fc1(inputs)
        outputs = self.act(outputs)
        outputs = self.fc2(outputs)
        outputs = self.act(outputs)
        outputs = self.fc3(outputs)
        outputs = self.act(outputs)
        outputs = self.fc4(outputs)
        outputs = self.act(outputs)
        outputs = self.fc5(outputs)
        outputs = F.sigmoid(outputs)
        return outputs

实例化RunnerV2类，启动模型训练，打印网络每层梯度值的ℓ2ℓ2范数。代码实现如下：

# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev],
            num_epochs=1, log_epochs=0,
            save_path="best_model.pdparams",
            custom_print_log=custom_print_log)

 运行结果为：

The weights of the Layers：
–>name: fc1.weight  –>grad_value: tensor([[0., 0.],
        [0., 0.],
        [0., 0.]])
———————————
–>name: fc1.bias  –>grad_value: tensor([0., 0., 0.])
———————————
–>name: fc2.weight  –>grad_value: tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])
———————————
–>name: fc2.bias  –>grad_value: tensor([0., 0., 0.])
———————————
–>name: fc3.weight  –>grad_value: tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])
———————————
–>name: fc3.bias  –>grad_value: tensor([0., 0., 0.])
———————————
–>name: fc4.weight  –>grad_value: tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])
———————————
–>name: fc4.bias  –>grad_value: tensor([0., 0., 0.])
———————————
–>name: fc5.weight  –>grad_value: tensor([[0., 0., 0.]])
———————————
–>name: fc5.bias  –>grad_value: tensor([-0.5106])
———————————
[Evaluate] best accuracy performence has been updated: 0.00000 –> 0.52500

       从输出结果可以发现，使用 ReLU 作为激活函数，当满足条件时，会发生死亡ReLU问题，网络训练过程中 ReLU 神经元的梯度始终为0，参数无法更新。

       针对死亡ReLU问题，一种简单有效的优化方式就是将激活函数更换为Leaky ReLU、ELU等ReLU 的变种。接下来，观察将激活函数更换为 Leaky ReLU时的梯度情况。

4.4.3.2 使用Leaky ReLU进行模型训练

将激活函数更换为Leaky ReLU进行模型训练，观察梯度情况。代码实现如下：

# 重新定义网络，使用Leaky ReLU激活函数
model =  Model_MLP_L5(input_size=2, output_size=1, act='lrelu')

# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev],
            num_epochs=1, log_epochps=None,
            save_path="best_model.pdparams",
            custom_print_log=custom_print_log)

运行结果为：

The weights of the Layers：
–>name: fc1.weight  –>grad_value: tensor([[-2.2568e-16,  3.5508e-17],
        [ 1.1090e-16, -1.7448e-17],
        [ 1.9872e-16, -3.1266e-17]])
———————————
–>name: fc1.bias  –>grad_value: tensor([-2.2717e-16,  1.1163e-16,  2.0003e-16])
———————————
–>name: fc2.weight  –>grad_value: tensor([[-1.6787e-14, -1.6798e-14, -1.6811e-14],
        [ 1.1792e-14,  1.1799e-14,  1.1809e-14],
        [-1.3686e-13, -1.3695e-13, -1.3706e-13]])
———————————
–>name: fc2.bias  –>grad_value: tensor([ 2.1013e-13, -1.4761e-13,  1.7131e-12])
———————————
–>name: fc3.weight  –>grad_value: tensor([[-6.6518e-10, -6.6498e-10, -6.6517e-10],
        [-1.2666e-10, -1.2662e-10, -1.2666e-10],
        [ 1.0642e-09,  1.0639e-09,  1.0642e-09]])
———————————
–>name: fc3.bias  –>grad_value: tensor([ 8.3144e-09,  1.5832e-09, -1.3302e-08])
———————————
–>name: fc4.weight  –>grad_value: tensor([[-6.6640e-07, -6.6628e-07, -6.6627e-07],
        [-2.9873e-06, -2.9867e-06, -2.9867e-06],
        [-5.7090e-06, -5.7080e-06, -5.7080e-06]])
———————————
–>name: fc4.bias  –>grad_value: tensor([8.3289e-06, 3.7336e-05, 7.1353e-05])
———————————
–>name: fc5.weight  –>grad_value: tensor([[0.0401, 0.0401, 0.0401]])
———————————
–>name: fc5.bias  –>grad_value: tensor([-0.5012])
———————————
[Evaluate] best accuracy performence has been updated: 0.00000 –> 0.55000
[Train] epoch: 0/1, loss: 4.011898994445801 

       从输出结果可以看到，将激活函数更换为Leaky ReLU后，死亡ReLU问题得到了改善，梯度恢复正常，参数也可以正常更新。但是由于 Leaky ReLU 中，x<0x<0 时的斜率默认只有0.01，所以反向传播时，随着网络层数的加深，梯度值越来越小。如果想要改善这一现象，将 Leaky ReLU 中，x<0x<0 时的斜率调大即可。 

  梯度消失与梯度爆炸的探究

首先先说一下什么是梯度爆炸和梯度消失，

先说一下啊我的理解，也就是老师上课讲的(可能当时下课了有人走了，但是我好好听了，就想写一下理解的）

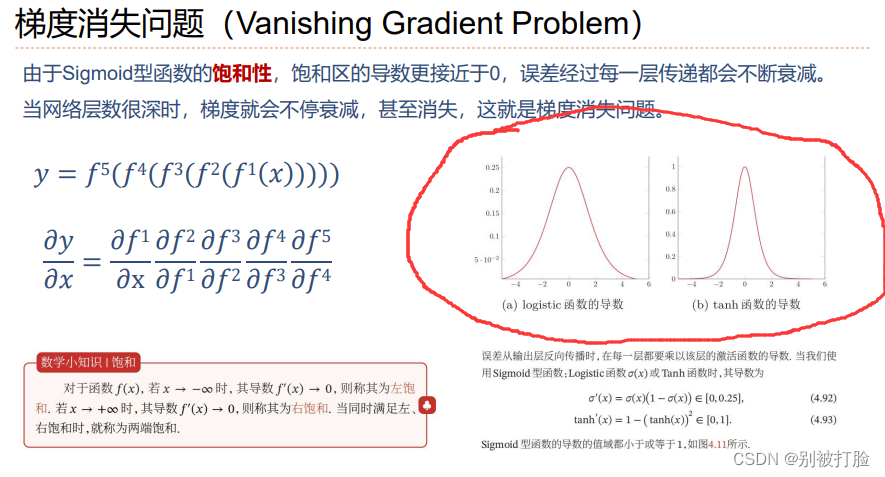
 梯度消失：其实，最直接的原因就是sigmoid型函数的导数，是小于1的，当层数过多，相乘会越来越趋于零，这就是上课老师说的核心意思，如上图

梯度爆炸：老师上课说的最直观的理解就是，相反的情况，一开始梯度较大，当层数过多是会呈现指数级增长，如下图。

从激活函数的角度来说：

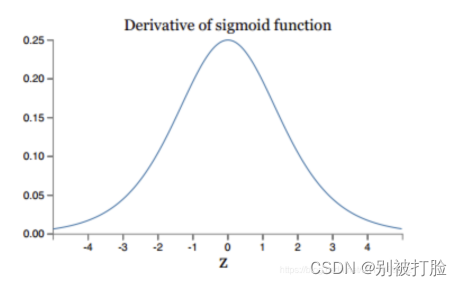
计算权值更新信息的时候需要计算前层偏导信息，因此如果激活函数选择不合适，比如使用sigmoid，梯度消失就会很明显了。上图是sigmoid的导数的图像，其梯度不会超过0.25，如果使用sigmoid作为损失函数，经过链式求导之后，很容易发生梯度消失。

一般的解决方案有：

• 好的参数初始化方式，如He初始化
• 非饱和的激活函数（如 ReLU）（较为常用）
• 批量规范化（Batch Normalization）
• 梯度截断（Gradient Clipping）
• 更快的优化器

       另外多说一句，其实Hinton大神提出capsule的原因就是为了彻底抛弃反向传播，因此，梯度消失、爆炸，其根本原因在于反向传播训练法则，属于先天不足(这是大神说的，我不敢)。

       但是，大神说话，我只需膜拜即可，说啥我听啥。

总结

首选，先说一下，又破纪录了，哈哈哈(真是痛并快乐着，但是我相信是值得的）

        然后，说一点有用的，这次写了好长时间，有点执着于找对应的库了，但是真的有所发现，发现了好多有用的东西。下边，是飞浆官方给的映射库，还一直在更新，真很有用。

          PyTorch 1.8 与 Paddle 2.0 API映射表-API文档-PaddlePaddle深度学习平台

       其次，这次理解了好多以前其实听过，或者甚至看达哥(吴恩达教授)的时候，达哥提到过的问题，但是以前并没有引起过注意，想对称权重的问题，梯度爆炸，梯度消失的问题，我感觉还是因为，以前练得少，没有写过所以没有啥感觉，这次写了写，才真的有感觉了。

       其次，这次自己又搭了搭模型，感觉这个真的是一个熟练的过程，每次其实，网络是差不多的，就是细节上的函数有点区别，我之前就说过，这个有点像搭积木，就是一块一块的往上放，这个感觉真的是在熟练，这个东西一定是要实践的。

       其次，这些把以前从达哥那个学的，以前从博客上学的，这次又找了点，感觉把超参数的调参真的弄的有点感觉了。这个感觉是很有用的。这个其实之前调参的时候，之前也说过不敢放手去调，这次又练了一练。

       其次，又深化了一下，自动微分求导，先说一个感觉，感觉老师上课讲课的PPT是真的有用，这次好多地方用到了,以前我用都是直接调用，因为别人都是直接调，我从来没考虑过为什么，这次终于是明白了。

       其次，明白了梯度爆炸和梯度消失的处理方法了，感觉又积累了一点。

       最后，河大的疫情越来约好了，期待着线下和老师的见面。

       最后，谢谢老师，在学习和生活上的关心(哈哈哈)。