IOU-loss
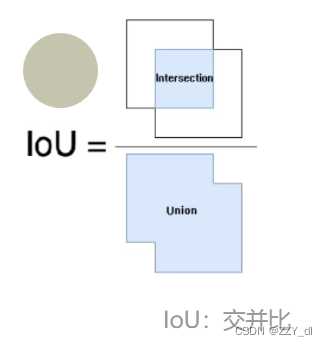
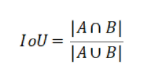
算法作用：Iou的就是交并比，预测框和真实框相交区域面积和合并区域面积的比值，计算公式如下，Iou作为损失函数的时候只要将其对数值输出就好了。
算法代码：
def Iou_loss(preds, bbox, eps=1e-6, reduction='mean'):
'''
preds:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
bbox:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
reduction:"mean"or"sum"
return: loss
'''
x1 = torch.max(preds[:, 0], bbox[:, 0])
y1 = torch.max(preds[:, 1], bbox[:, 1])
x2 = torch.min(preds[:, 2], bbox[:, 2])
y2 = torch.min(preds[:, 3], bbox[:, 3])
w = (x2 - x1 + 1.0).clamp(0.)
h = (y2 - y1 + 1.0).clamp(0.)
inters = w * h
print("inters:\n",inters)
uni = (preds[:, 2] - preds[:, 0] + 1.0) * (preds[:, 3] - preds[:, 1] + 1.0) + (bbox[:, 2] - bbox[:, 0] + 1.0) * (
bbox[:, 3] - bbox[:, 1] + 1.0) - inters
print("uni:\n",uni)
ious = (inters / uni).clamp(min=eps)
loss = -ious.log()
if reduction == 'mean':
loss = torch.mean(loss)
elif reduction == 'sum':
loss = torch.sum(loss)
else:
raise NotImplementedError
print("last_loss:\n",loss)
return loss
if __name__ == "__main__":
pred_box = torch.tensor([[2,4,6,8],[5,9,13,12]])
gt_box = torch.tensor([[3,4,7,9]])
loss = Iou_loss(preds=pred_box,bbox=gt_box)
# 输出结果
"""
inters:
tensor([20., 3.])
uni:
tensor([35., 63.])
last_loss:
tensor(1.8021)
"""
GIOU-loss
问题分析
当预测框和真实框不相交时Iou值为0，导致很大范围内损失函数没有梯度。针对这一问题，提出了Giou作为损失函数。
算法公式及其解释：其实想法也很简单（但这一步很难）：假如现在有两个box A，B，我们找到一个最小的封闭形状C，让C可以把A，B包含在内，然后再计算C中没有覆盖A和B的面积占C总面积的比值，然后用A与B的IoU减去这个比值：
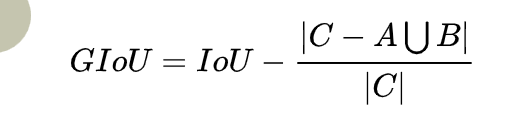
GIoU其实一种泛化版的IoU，是IoU的下界，与IoU只关注重叠部分不同，GIoU不仅关注重叠区域，还关注其他非重合区域，能更好地反映二者的重合度。
算法代码：
def Giou_loss(preds, bbox, eps=1e-7, reduction='mean'):
'''
https://github.com/sfzhang15/ATSS/blob/master/atss_core/modeling/rpn/atss/loss.py#L36
:param preds:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
:param bbox:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
:return: loss
'''
ix1 = torch.max(preds[:, 0], bbox[:, 0])
iy1 = torch.max(preds[:, 1], bbox[:, 1])
ix2 = torch.min(preds[:, 2], bbox[:, 2])
iy2 = torch.min(preds[:, 3], bbox[:, 3])
iw = (ix2 - ix1 + 1.0).clamp(0.)
ih = (iy2 - iy1 + 1.0).clamp(0.)
# overlap
inters = iw * ih
print("inters:\n",inters)
# union
uni = (preds[:, 2] - preds[:, 0] + 1.0) * (preds[:, 3] - preds[:, 1] + 1.0) + (bbox[:, 2] - bbox[:, 0] + 1.0) * (
bbox[:, 3] - bbox[:, 1] + 1.0) - inters + eps
print("uni:\n",uni)
# ious
ious = inters / uni
print("Iou:\n",ious)
ex1 = torch.min(preds[:, 0], bbox[:, 0])
ey1 = torch.min(preds[:, 1], bbox[:, 1])
ex2 = torch.max(preds[:, 2], bbox[:, 2])
ey2 = torch.max(preds[:, 3], bbox[:, 3])
ew = (ex2 - ex1 + 1.0).clamp(min=0.)
eh = (ey2 - ey1 + 1.0).clamp(min=0.)
# enclose erea
enclose = ew * eh + eps
print("enclose:\n",enclose)
giou = ious - (enclose - uni) / enclose
loss = 1 - giou
if reduction == 'mean':
loss = torch.mean(loss)
elif reduction == 'sum':
loss = torch.sum(loss)
else:
raise NotImplementedError
print("last_loss:\n",loss)
return loss
if __name__ == "__main__":
pred_box = torch.tensor([[2,4,6,8],[5,9,13,12]])
gt_box = torch.tensor([[3,4,7,9]])
loss = Giou_loss(preds=pred_box,bbox=gt_box)
# 输出结果
"""
inters:
tensor([20., 3.])
uni:
tensor([35., 63.])
Iou:
tensor([0.5714, 0.0476])
enclose:
tensor([36., 99.])
last_loss:
tensor(0.8862)
"""
DIOU-loss
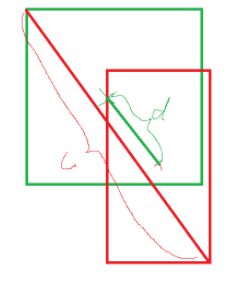
问题分析
虽然GIoU可以缓解不重叠情况下梯度消失问题，但是它依然存在一些局限性。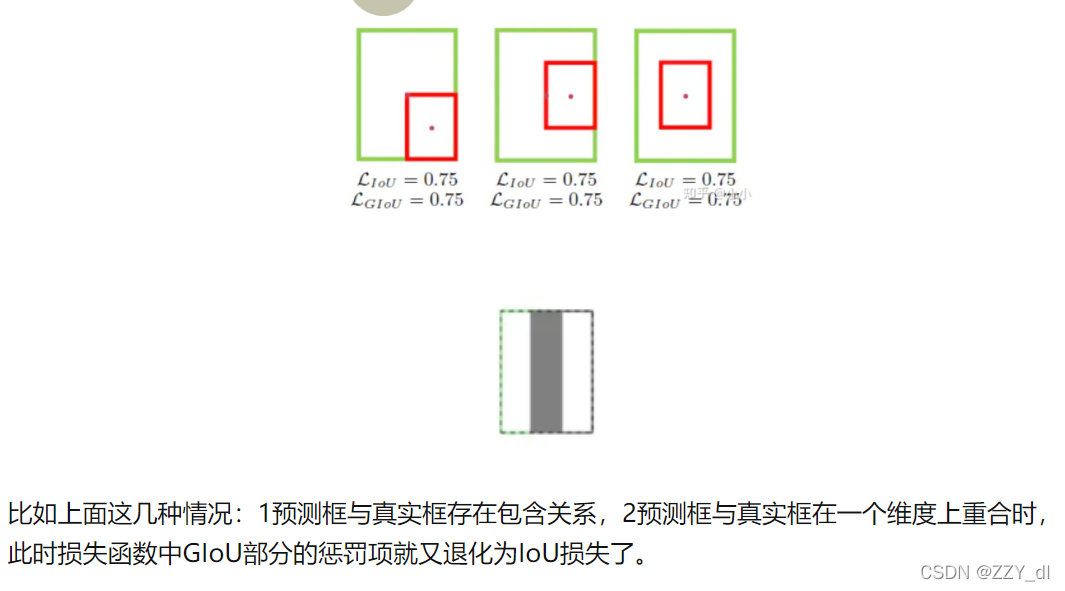
基于IoU和GIoU存在的问题，作者提出了两个问题：
- 直接最小化anchor框与目标框之间的归一化距离是否可行，以达到更快的收敛速度？
- 如何使回归在与目标框有重叠甚至包含时更准确、更快？
其实在边界框回归的过程中需要考虑的几点：
- 重叠面积
- 中心点距离
- 长宽比
实际上，无论是IoU还是GIoU都只考虑了第一点重叠面积。因此提出的DIoU中考虑了第二点中心点距离。
算法公式及其解释：
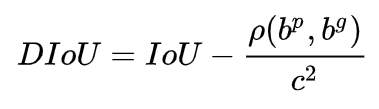
def Diou_loss(preds, bbox, eps=1e-7, reduction='mean'):
'''
preds:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
bbox:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
eps: eps to avoid divide 0
reduction: mean or sum
return: diou-loss
'''
ix1 = torch.max(preds[:, 0], bbox[:, 0])
iy1 = torch.max(preds[:, 1], bbox[:, 1])
ix2 = torch.min(preds[:, 2], bbox[:, 2])
iy2 = torch.min(preds[:, 3], bbox[:, 3])
iw = (ix2 - ix1 + 1.0).clamp(min=0.)
ih = (iy2 - iy1 + 1.0).clamp(min=0.)
# overlaps
inters = iw * ih
# union
uni = (preds[:, 2] - preds[:, 0] + 1.0) * (preds[:, 3] - preds[:, 1] + 1.0) + (bbox[:, 2] - bbox[:, 0] + 1.0) * (
bbox[:, 3] - bbox[:, 1] + 1.0) - inters
# iou
iou = inters / (uni + eps)
print("iou:\n",iou)
# inter_diag
cxpreds = (preds[:, 2] + preds[:, 0]) / 2
cypreds = (preds[:, 3] + preds[:, 1]) / 2
cxbbox = (bbox[:, 2] + bbox[:, 0]) / 2
cybbox = (bbox[:, 3] + bbox[:, 1]) / 2
inter_diag = (cxbbox - cxpreds) ** 2 + (cybbox - cypreds) ** 2
print("inter_diag:\n",inter_diag)
# outer_diag
ox1 = torch.min(preds[:, 0], bbox[:, 0])
oy1 = torch.min(preds[:, 1], bbox[:, 1])
ox2 = torch.max(preds[:, 2], bbox[:, 2])
oy2 = torch.max(preds[:, 3], bbox[:, 3])
outer_diag = (ox1 - ox2) ** 2 + (oy1 - oy2) ** 2
print("outer_diag:\n",outer_diag)
diou = iou - inter_diag / outer_diag
diou = torch.clamp(diou, min=-1.0, max=1.0)
diou_loss = 1 - diou
print("last_loss:\n",diou_loss)
if reduction == 'mean':
loss = torch.mean(diou_loss)
elif reduction == 'sum':
loss = torch.sum(diou_loss)
else:
raise NotImplementedError
return loss
if __name__ == "__main__":
pred_box = torch.tensor([[2,4,6,8],[5,9,13,12]])
gt_box = torch.tensor([[3,4,7,9]])
loss = Diou_loss(preds=pred_box,bbox=gt_box)
# 输出结果
"""
iou:
tensor([0.5714, 0.0476])
inter_diag:
tensor([ 1, 32])
outer_diag:
tensor([ 50, 164])
last_loss:
tensor([0.4286, 0.9524])
"""
CIOU-loss
问题分析
Ciou在Diou的基础上进行改进，认为Diou只考虑了中心点距离和重叠面积，但是没有考虑到长宽比。
算法公式及其解释：
算法代码：
import math
def Ciou_loss(preds, bbox, eps=1e-7, reduction='mean'):
'''
https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/loss/multibox_loss.py
:param preds:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
:param bbox:[[x1,y1,x2,y2], [x1,y1,x2,y2],,,]
:param eps: eps to avoid divide 0
:param reduction: mean or sum
:return: diou-loss
'''
ix1 = torch.max(preds[:, 0], bbox[:, 0])
iy1 = torch.max(preds[:, 1], bbox[:, 1])
ix2 = torch.min(preds[:, 2], bbox[:, 2])
iy2 = torch.min(preds[:, 3], bbox[:, 3])
iw = (ix2 - ix1 + 1.0).clamp(min=0.)
ih = (iy2 - iy1 + 1.0).clamp(min=0.)
# overlaps
inters = iw * ih
# union
uni = (preds[:, 2] - preds[:, 0] + 1.0) * (preds[:, 3] - preds[:, 1] + 1.0) + (bbox[:, 2] - bbox[:, 0] + 1.0) * (
bbox[:, 3] - bbox[:, 1] + 1.0) - inters
# iou
iou = inters / (uni + eps)
print("iou:\n",iou)
# inter_diag
cxpreds = (preds[:, 2] + preds[:, 0]) / 2
cypreds = (preds[:, 3] + preds[:, 1]) / 2
cxbbox = (bbox[:, 2] + bbox[:, 0]) / 2
cybbox = (bbox[:, 3] + bbox[:, 1]) / 2
inter_diag = (cxbbox - cxpreds) ** 2 + (cybbox - cypreds) ** 2
# outer_diag
ox1 = torch.min(preds[:, 0], bbox[:, 0])
oy1 = torch.min(preds[:, 1], bbox[:, 1])
ox2 = torch.max(preds[:, 2], bbox[:, 2])
oy2 = torch.max(preds[:, 3], bbox[:, 3])
outer_diag = (ox1 - ox2) ** 2 + (oy1 - oy2) ** 2
diou = iou - inter_diag / outer_diag
print("diou:\n",diou)
# calculate v,alpha
wbbox = bbox[:, 2] - bbox[:, 0] + 1.0
hbbox = bbox[:, 3] - bbox[:, 1] + 1.0
wpreds = preds[:, 2] - preds[:, 0] + 1.0
hpreds = preds[:, 3] - preds[:, 1] + 1.0
v = torch.pow((torch.atan(wbbox / hbbox) - torch.atan(wpreds / hpreds)), 2) * (4 / (math.pi ** 2))
alpha = v / (1 - iou + v)
ciou = diou - alpha * v
ciou = torch.clamp(ciou, min=-1.0, max=1.0)
ciou_loss = 1 - ciou
if reduction == 'mean':
loss = torch.mean(ciou_loss)
elif reduction == 'sum':
loss = torch.sum(ciou_loss)
else:
raise NotImplementedError
print("last_loss:\n",loss)
return loss
if __name__ == "__main__":
pred_box = torch.tensor([[2,4,6,8],[5,9,13,12]])
gt_box = torch.tensor([[3,4,7,9]])
loss = Ciou_loss(preds=pred_box,bbox=gt_box)
# 输出结果
"""
iou:
tensor([0.5714, 0.0476])
diou:
tensor([0.5714, 0.0476])
last_loss:
tensor(0.6940)
"""
EIOU-loss和Focal EIOU-loss
文章链接：点击
存在的问题
CIOU Loss虽然考虑了边界框回归的重叠面积、中心点距离、纵横比。但是通过其公式中的v反映的纵横比的差异，而不是宽高分别与其置信度的真实差异，所以有时会阻碍模型有效的优化相似性。针对这一问题，有学者在CIOU的基础上将纵横比拆开，提出了EIOU Loss，并且加入Focal聚焦优质的锚框，该方法出自于2021年的一篇文章《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》
算法公式及其解释：
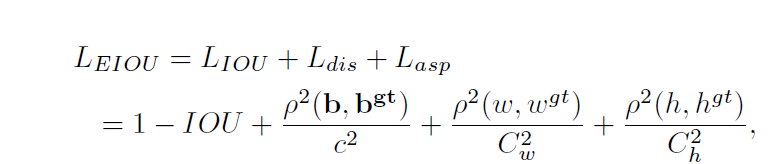该损失函数包含三个部分：重叠损失，中心距离损失，宽高损失，前两部分延续CIOU中的方法，但是宽高损失直接使目标盒与锚盒的宽度和高度之差最小，使得收敛速度更快。其中 Cw 和 Ch 是覆盖两个Box的最小外接框的宽度和高度。考虑到
BBox的回归中也存在训练样本不平衡的问题，即在一张图像中回归误差小的高质量锚框的数量远少于误差大的低质量样本，质量较差的样本会产生过大的梯度影响训练过程。作者在
EIOU的基础上结合Focal Loss提出一种Focal EIOU Loss，梯度的角度出发，把高质量的锚框和低质量的锚框分开，公式如下
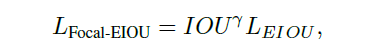
其中IOU = |A∩B|/|A∪B|， γ为控制异常值抑制程度的参数。该损失中的Focal与传统的Focal Loss有一定的区别，传统的Focal Loss针对越困难的样本损失越大，起到的是困难样本挖掘的作用；而根据上述公式：IOU越高的损失越大，相当于加权作用，给越好的回归目标一个越大的损失，有助于提高回归精度。
存在的问题
本文针对边界框回归任务，在之前基于CIOU损失的基础上提出了两个优化方法：
- 将纵横比的损失项拆分成预测的宽高分别与最小外接框宽高的差值，加速了收敛提高了回归精度；
- 引入了Focal Loss优化了边界框回归任务中的样本不平衡问题，即减少与目标框重叠较少的大量锚框对BBox 回归的优化贡献，使回归过程专注于高质量锚框。
不足之处或许在于Focal的表达形式是否有待改进。
算法代码
def bbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False, EIoU=False, eps=1e-7):
# Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
box2 = box2.T
# Get the coordinates of bounding boxes
if x1y1x2y2: # x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
else: # transform from xywh to xyxy
b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2
# Intersection area
inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
(torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)
# Union Area
w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
union = w1 * h1 + w2 * h2 - inter + eps
iou = inter / union
if GIoU or DIoU or CIoU or EIoU:
cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1) # convex (smallest enclosing box) width
ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1) # convex height
if CIoU or DIoU or EIoU: # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
c2 = cw ** 2 + ch ** 2 + eps # convex diagonal squared
rho2 = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 +
(b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4 # center distance squared
if DIoU:
return iou - rho2 / c2 # DIoU
elif CIoU: # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
with torch.no_grad():
alpha = v / (v - iou + (1 + eps))
return iou - (rho2 / c2 + v * alpha) # CIoU
elif EIoU:
rho_w2 = ((b2_x2 - b2_x1) - (b1_x2 - b1_x1)) ** 2
rho_h2 = ((b2_y2 - b2_y1) - (b1_y2 - b1_y1)) ** 2
cw2 = cw ** 2 + eps
ch2 = ch ** 2 + eps
return iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2)
else: # GIoU https://arxiv.org/pdf/1902.09630.pdf
c_area = cw * ch + eps # convex area
return iou - (c_area - union) / c_area # GIoU
else:
return iou # IoU
alpha IOU
算法代码：
def bbox_alpha_iou(box1, box2, x1y1x2y2=False, GIoU=False, DIoU=False, CIoU=False, alpha=3, eps=1e-7):
# Returns tsqrt_he IoU of box1 to box2. box1 is 4, box2 is nx4
box2 = box2.T
# Get the coordinates of bounding boxes
if x1y1x2y2: # x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
else: # transform from xywh to xyxy
b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2
# Intersection area
inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
(torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)
# Union Area
w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
union = w1 * h1 + w2 * h2 - inter + eps
# change iou into pow(iou+eps)
# iou = inter / union
iou = torch.pow(inter/union + eps, alpha)
# beta = 2 * alpha
if GIoU or DIoU or CIoU:
cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1) # convex (smallest enclosing box) width
ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1) # convex height
if CIoU or DIoU: # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
c2 = (cw ** 2 + ch ** 2) ** alpha + eps # convex diagonal
rho_x = torch.abs(b2_x1 + b2_x2 - b1_x1 - b1_x2)
rho_y = torch.abs(b2_y1 + b2_y2 - b1_y1 - b1_y2)
rho2 = ((rho_x ** 2 + rho_y ** 2) / 4) ** alpha # center distance
if DIoU:
return iou - rho2 / c2 # DIoU
elif CIoU: # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
with torch.no_grad():
alpha_ciou = v / ((1 + eps) - inter / union + v)
# return iou - (rho2 / c2 + v * alpha_ciou) # CIoU
return iou - (rho2 / c2 + torch.pow(v * alpha_ciou + eps, alpha)) # CIoU
else: # GIoU https://arxiv.org/pdf/1902.09630.pdf
# c_area = cw * ch + eps # convex area
# return iou - (c_area - union) / c_area # GIoU
c_area = torch.max(cw * ch + eps, union) # convex area
return iou - torch.pow((c_area - union) / c_area + eps, alpha) # GIoU
else:
return iou # torch.log(iou+eps) or iou
总对比
边界框回归的三大几何因素：重叠面积、中心点距离、纵横比
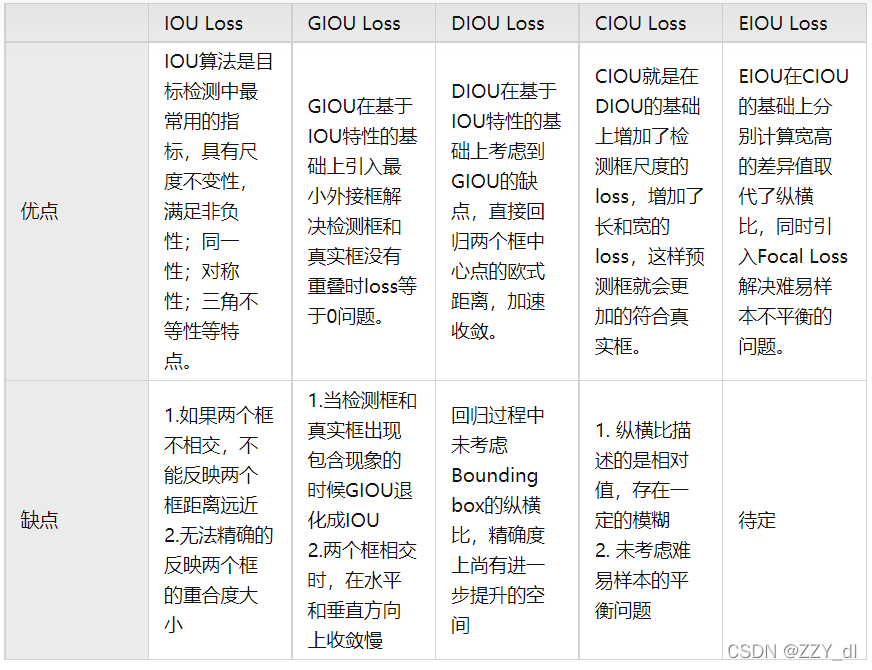
IOU Loss：考虑了重叠面积，归一化坐标尺度；
GIOU Loss：考虑了重叠面积，基于IOU解决边界框不相交时loss等于0的问题；
DIOU Loss：考虑了重叠面积和中心点距离，基于IOU解决GIOU收敛慢的问题；
CIOU Loss：考虑了重叠面积、中心点距离、纵横比，基于DIOU提升回归精确度；
EIOU Loss：考虑了重叠面积，中心点距离、长宽边长真实差，基于CIOU解决了纵横比的模糊定义，并添加Focal Loss解决BBox回归中的样本不平衡问题。
参考链接：
文章出处登录后可见！
已经登录？立即刷新
