前言：

1.这篇文章是对本人该学期强化学习课程作业的整合与概括，仅作为强化学习的入手练习，因此难免会有诸多的疏漏，还请包涵。

2.信息获取的部分主要参照了B站up蓝魔digital的强化学习&机器学习打只狼教程【B站链接】，这位大佬所使用的方法简单易用，并且可以拓展运用在除了只狼以外的任意一款游戏中，感兴趣的大佬们也可以自己试一试，可以肯定的说，运用与尝试的过程极其有趣。

3.之所以选用《只狼》与《黑魂》，是因为它们作为角色扮演动作游戏，与其它许多游戏有着诸多的不同，一是由于我们能通过一些人为的约束，有效地减少输入动作的数量，并且使其在仅使用少数几种动作的情况下也能达到训练的目的（例如击杀某只精英怪，或者是击杀某位boss）

4.由于时间和能力有限，在本文中仅仅使用了最简单DQN结构与AC结构。

1.DQN的基础理论

首先，我们假定在看这篇文章的你对强化学习中的一些简单模型已经有了一定的了解（如果没有，这么简单好学又有趣的东西不妨先自学一下）。我们以SARSA与Q-learning为例，它们都将动作值函数存储到一个“表格”中，并用表格中的数据来评价不同状态下的不同动作。若状态和动作空间是离散且维度不高时，是比较有效的；若状态和动作空间是高维连续时，就会出现“curse of dimensionality”，即随着维数的增加，计算量呈指数倍增长。

价值函数逼近

既然我们无法用一个表格来精确地存储与表示 Q 值，我们可以用一个 parameterized 函数来近似地表示动作值函数 $Q(s,a)$ ，即

$Q(s,a) = f(s,a,\theta )$

有很多 differentiable function approximators，如：

线性模型（Linear combinations of features）
神经网路（Neural network）
决策树（Decision tree）
最近邻（Nearest neighbour）
…

DQN

DQN（Deep Q-Network）是深度强化学习（Deep Reinforcement Learning）的开山之作，将深度学习引入强化学习中，构建了 Perception 到 Decision 的 End-to-end 架构。DQN 最开始由 DeepMind 发表在 NIPS 2013，后来将改进的版本发表在 Nature 2015。

深度学习是监督学习。计算损失函数需要标签数据，通过梯度下降和误差反向传播更新神经网络的参数。如何在强化学习中获取标签？

回想上文 Q-learning 中，我们用 $R{_{t+1}}+\gamma\underset{a}{max}Q(S_{t+1} , \alpha )$ 来更新 Q 值，在这里我们可以将其作为标签 Q 值（TargetNet）：

$R{_{t+1}}+\gamma\underset{a}{max}Q(S_{t+1} , \alpha ;\theta )$

经验回放 Experience Replay

DQN 面临着几个挑战：

深度学习需要大量带标签的训练数据；
强化学习从 scalar reward 进行学习，但是 reward 经常是 sparse, noisy, delayed；
深度学习假设样本数据是独立同分布的，但强化学习中采样的数据是强相关的

因此，DQN 采用经验回放（Experience Replay）机制，将训练过的数据进行储存到 Replay Buffer 中，以便后续从中随机采样进行训练，好处就是：1. 数据利用率高；2. 减少连续样本的相关性，从而减小方差（variance）。

NIP 2013 中 DQN 的伪代码如下图所示：

Nature 2015 中 DQN 做了改进，提出了一个目标网络(Target Net)与策略网络(Policy Net)的结构，每经过N个回合，目标网络会自动获取策略网络的参数，这一改动的目的主要是为了使训练过程更加稳定可控。

整个DQN的流程图如下所示：

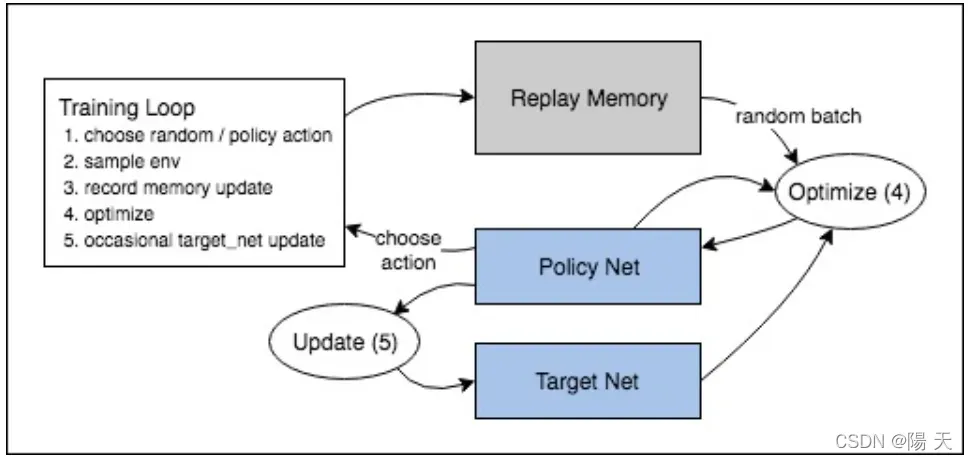
2.AC框架

在正式开始讨论Actor-Critic算法之前，我想先谈论一下PG算法。

在PG算法中，我们的Agent又被称为Actor，Actor对于一个特定的任务，都有自己的一个策略π，策略π通常用一个神经网络表示，其参数为θ。从一个特定的状态state出发，一直到任务的结束，被称为一个完整的eposide，在每一步，我们都能获得一个奖励r，一个完整的任务所获得的最终奖励被称为R。这样，一个有T个时刻的eposide，Actor不断与环境交互，形成如下的序列：

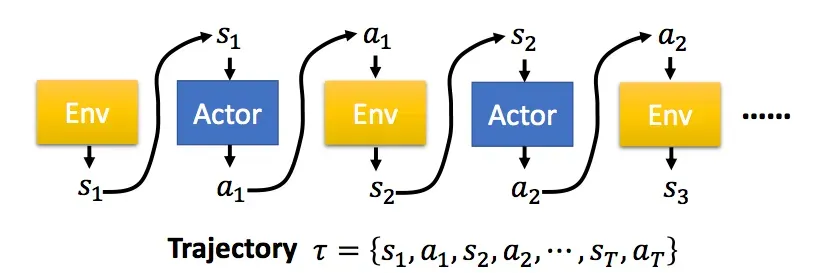
PG算法将离散动作空间拓展到了连续动作空间。我们的目标是要寻找一个能够使期望收益达到最大的策略，并沿着梯度方向更新其参数 $\theta$ 。

Actor-Critic算法分为两部分，actor的前身是policy gradient，它可以轻松地在连续动作空间内选择合适的动作，value-based的Q-learning只能解决离散动作空间的问题。但是又因为Actor是基于一个episode的return来进行更新的，所以学习效率比较慢。这时候我们发现使用一个value-based的算法作为Critic就可以使用TD方法实现单步更新，这其实可以看做是拿偏差换方差。这样两种算法相互补充就形成了我们的Actor-Critic。

Actor 基于概率分布选择行为, Critic 基于 Actor 生成的行为评判得分, Actor 再根据 Critic 的评分修改选行为的概率。

优点：可以进行单步更新，不需要跑完一个episode再更新网络参数，相较于传统的PG更新更快。传统PG对价值的估计虽然是无偏的，但方差较大，AC方法牺牲了一点偏差，但能够有效降低方差；
缺点：Actor的行为取决于 Critic 的Value，但是因为 Critic本身就很难收敛和actor一起更新的话就更难收敛了。（为了解决收敛问题， Deepmind 提出了 Actor Critic 升级版 Deep Deterministic Policy Gradient，后者融合了 DQN 的一些 trick, 解决了收敛难的问题）。

AC算法的流程图如下：

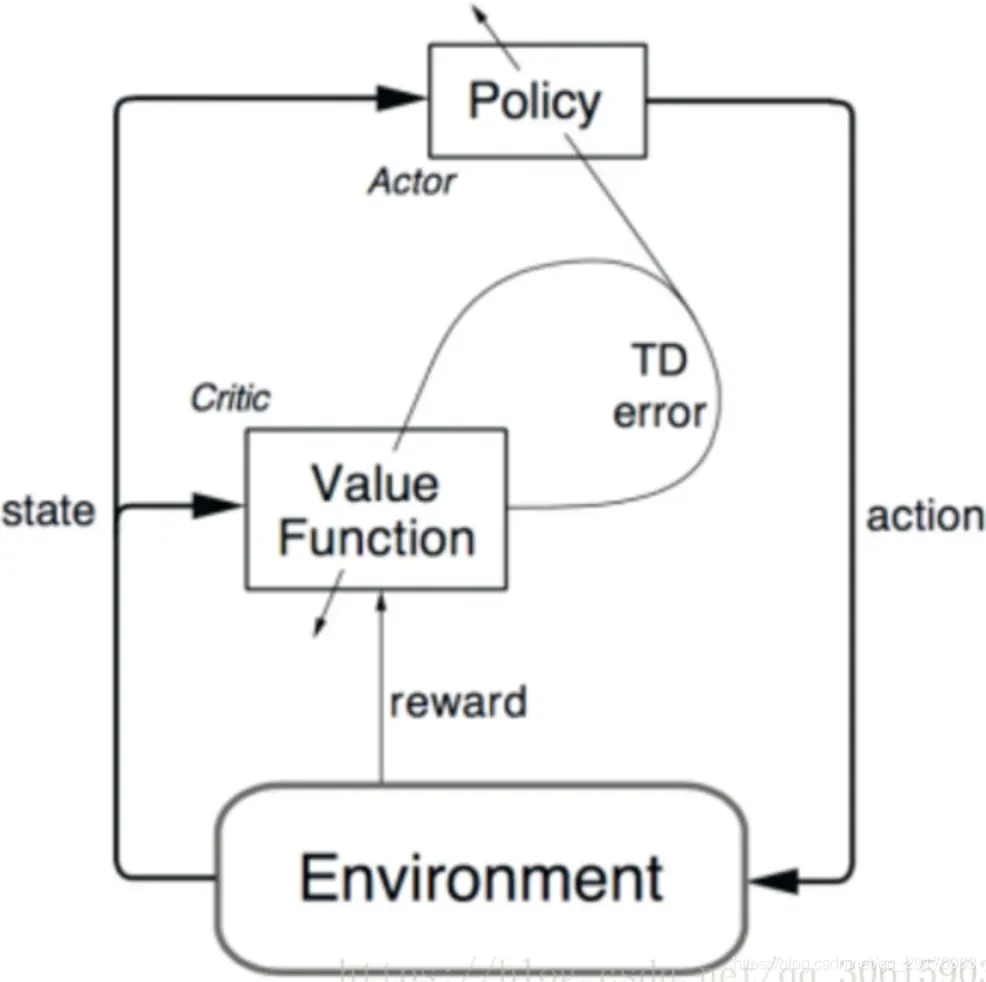
总的来说，AC算法能够将动作从离散空间拓展到连续空间上，因此在本实验中，我们主要尝试通过AC框架去制定一个SPG，并将其与DQN进行对比。

3.游戏的选择与信息的获取（以只狼为例）

经过前面“冗长”“枯燥”的理论铺垫，我们终于可以进入最有趣的部分了。现在我们可以开始尝试了。
作为实验的对象，我们选择了《只狼影逝二度》与《黑暗之魂2 原罪学者》两款游戏（魂1和魂3都很好玩儿，但是魂2永远是我的白月光）

首先，只狼与黑魂有着诸多的共同点，它们都属于魂系列（废话），它们有着相近的游戏模式：我们需要操控我们的主角，击败各种敌人，且主角可以进行的动作包括攻击、闪避/翻滚、防御、锁定以及各种特殊的攻击方式。最重要的是，我们可以用相似的方法去获取游戏画面中的信息。

不管是黑魂还是狼，我们最需要注意的就是自己的状态（包括血量，狼中的姿势条，黑魂中的体力条，各种异常状态，敌人的血量）量、敌我关系、位置等）。以这位大佬的帖子【链接】中的图片为例：

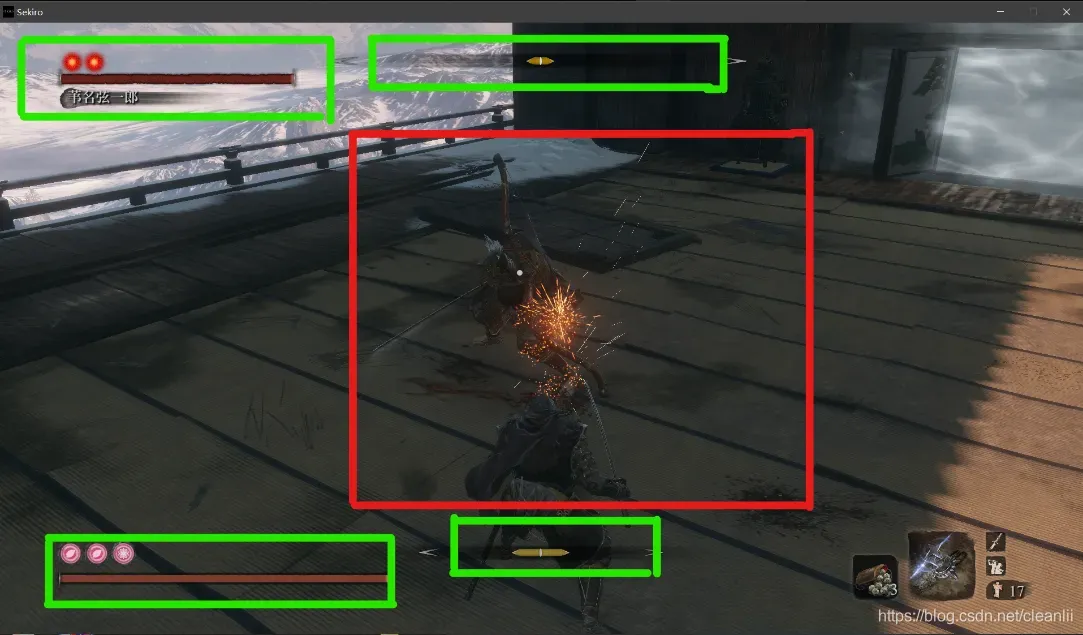
我们可以将需要获取的信息笼统地概括为两个部分，正如图中的绿色框与红色框所示。绿色框内包括自身的血量、敌人的血量、自身的架势值与敌人的架势值，我们要根据这些信息计算每一个动作的reward。红色框内包括主角的状态与敌人的状态，得益于黑魂与只狼的锁定视角，我们仅需截取屏幕中间的一块区域就可以获取相对完整的信息，不论是在DQN还是AC结构中，我们所要做的都是将红色区域的部分输入卷积神经网络中，接下来的事情很简单，就是依照AC算法或者DQN算法的流程图，结合绿色框内的信息一步一步进行下去。

同理，在黑暗之魂2中，我们依旧需要关注这些内容，红色框内是锁定状态下角色与敌人之间的状态（这张图中没有敌人，所以我摆了个pose），而绿色框内则代表角色的血量与耐力条，我们对这些信息进行与只狼中类似的处理。

关于具体的自身血量、敌人血量的量化方式，本文借鉴了【B站up主蓝魔digital的方法】

而只狼中的架势条量化方法，则借鉴了另外一位大佬所使用的Canny边缘检验【csdn链接】

4.代码

DQN的部分代码

def PressKey(hexKeyCode):
    extra = ctypes.c_ulong(0)
    ii_ = Input_I()
    ii_.ki = KeyBdInput( 0, hexKeyCode, 0x0008, 0, ctypes.pointer(extra) )
    x = Input( ctypes.c_ulong(1), ii_ )
    ctypes.windll.user32.SendInput(1, ctypes.pointer(x), ctypes.sizeof(x))

def ReleaseKey(hexKeyCode):
    extra = ctypes.c_ulong(0)
    ii_ = Input_I()
    ii_.ki = KeyBdInput( 0, hexKeyCode, 0x0008 | 0x0002, 0, ctypes.pointer(extra) )
    x = Input( ctypes.c_ulong(1), ii_ )
    ctypes.windll.user32.SendInput(1, ctypes.pointer(x), ctypes.sizeof(x))

这一段代码的作用主要是为了模仿键盘的输入，整个过程由两个重要的函数组成，PressKey代表按下对应的按键，而ReleaseKey代表松开对应的按键，如果两个函数执行的间隔时间极短，那么就可以认为我们快速地敲击了一下对应的按键；而如果两个函数之间执行的间隔时间较长，则代表我们按下了对应的按键，并在一段时间后松开。

那么接下来，如果我们需要人物执行一次对应的动作，例如，如果我们将向左移动的按键设置为键盘上的A键，那么使角色向左侧移动一次的函数就可以表示成：

def go_left():
    PressKey(A)
    time.sleep(0.4)
    ReleaseKey(A)

首先按下键盘上的A键，然后隔一段时间（0.4s）后松开A键，这样就完成了一次移动。通过使用相同的方法，我们可以令角色做出不同的动作。

接下来是角色信息的获取。由于上一篇文章已经介绍了该方法，所以这里重点介绍代码：

def self_blood_count(self_gray):
    self_blood = 0
    for self_bd_num in self_gray[-2]:
        # self blood gray pixel 80~98
        # 血量灰度值80~98
        if self_bd_num > 90 and self_bd_num < 98:
            self_blood += 1
    return self_blood

def boss_blood_count(boss_gray):
    boss_blood = 0
    for boss_bd_num in boss_gray[0]:
    # boss blood gray pixel 65~75
    # 血量灰度值65~75 
        if boss_bd_num > 65 and boss_bd_num < 75:
            boss_blood += 1
    return boss_blood

上面展示的是获取自身血量信息与boss血量信息的函数，我们所做的主要工作是，截取图像中的自身血量或者敌人血量所在的行，然后计算在这一行中，有多少个特定灰度值的像素点。打个比方，如果在灰度化后的图像中，人物血量的灰度值在90与98之间，那么我们只需要计算在这一行中有多少像素点的灰度值在这一范围内，就可以得到人物的血量。通过使用相同的方法，我们也可以得到敌人的血量。

除此之外，游戏画面中除了“血量”这一信息外，还有包括耐力条（魂二）与架势条之类的信息，在这之中，耐力条可以通过上面所展示的方法获取；但架势条的获取较为复杂，因为架势条的颜色会随着值的增加而不断变深，这就使得我们用相同的方法去获取架势条的信息时，会遭遇许许多多的问题。对此我们所使用的方法是Canny算子边缘检测。

def get_self_HP(img):
	img = ROI(img, x=48, x_w=307, y=406, y_h=410)
	canny = cv2.Canny(cv2.GaussianBlur(img,(3,3),0), 0, 100)
	value = canny.argmax(axis=-1)
	return np.median(value)

有了信息获取的步骤后，我们接下来所需要做的就是构建我们所需要的网络，我们所使用的DQN结构如下所示：

class DQN():
    def __init__(self, observation_width, observation_height, action_space, model_file, log_file):
        # the state is the input vector of network, in this env, it has four dimensions
        self.state_dim = observation_width * observation_height
        self.state_w = observation_width
        self.state_h = observation_height
        # the action is the output vector and it has two dimensions
        self.action_dim = action_space
        # init experience replay, the deque is a list that first-in & first-out
        self.replay_buffer = deque()
        # you can create the network by the two parameters
        self.create_Q_network()
        # after create the network, we can define the training methods
        self.create_updating_method()
        # set the value in choose_action
        self.epsilon = INITIAL_EPSILON
    
    # the function that give the weight initial value
    def weight_variable(self, shape):
        initial = tf.truncated_normal(shape, stddev=0.1)
        return tf.Variable(initial)

    # the function that give the bias initial value
    def bias_variable(self, shape):
        initial = tf.constant(0.01, shape=shape)
        return tf.Variable(initial)
    
    def conv2d(self, x, W):
        return tf.nn.conv2d(x, W, strides=[1,1,1,1], padding='SAME')
        # stride第一个和最后一个元素一定要为1，中间两个分别是x和y轴的跨度，此处设为1
        # SAME 抽取时外面有填充，抽取大小是一样的
    
    def max_pool_2x2(self, x):
        return tf.nn.max_pool(x, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME')

def create_Q_network(self):
        with tf.name_scope('inputs'):
            # first, set the input of networks
            self.state_input = tf.placeholder("float", [None, self.state_h, self.state_w, 1])
        # second, create the current_net
        with tf.variable_scope('current_net'):
            W_conv1 = self.weight_variable([5,5,1,32])
            b_conv1 = self.bias_variable([32])
            W_conv2 = self.weight_variable([5,5,32,64])
            b_conv2 = self.bias_variable([64])
            W1 = self.weight_variable([int((self.state_w/4) * (self.state_h/4) * 64), 512])
            b1 = self.bias_variable([512])
            W2 = self.weight_variable([512, 256])
            b2 = self.bias_variable([256])
            W3 = self.weight_variable([256, self.action_dim])
            b3 = self.bias_variable([self.action_dim])
            h_conv1 = tf.nn.relu(self.conv2d(self.state_input, W_conv1) + b_conv1)   
            h_pool1 = self.max_pool_2x2(h_conv1)    
            h_conv2 = tf.nn.relu(self.conv2d(h_pool1, W_conv2) + b_conv2) 
            h_pool2 = self.max_pool_2x2(h_conv2) 
            h_conv2_flat = tf.reshape(h_pool2, [-1,int((self.state_w/4) * (self.state_h/4) * 64)])
            h_layer_one = tf.nn.relu(tf.matmul(h_conv2_flat, W1) + b1)
            h_layer_one = tf.nn.dropout(h_layer_one, 1)
            h_layer_two = tf.nn.relu(tf.matmul(h_layer_one, W2) + b2)
            h_layer_two = tf.nn.dropout(h_layer_two, 1)
            Q_value = tf.matmul(h_layer_two, W3) + b3
            # dropout
            self.Q_value = tf.nn.dropout(Q_value, 1)
        # third, create the current_net
        with tf.variable_scope('target_net'):
            # first, set the network's weights
            t_W_conv1 = self.weight_variable([5,5,1,32])
            t_b_conv1 = self.bias_variable([32])
            t_W_conv2 = self.weight_variable([5,5,32,64])
            t_b_conv2 = self.bias_variable([64])
            t_W1 = self.weight_variable([int((self.state_w/4) * (self.state_h/4) * 64), 512])
            t_b1 = self.bias_variable([512])
            t_W2 = self.weight_variable([512, 256])
            t_b2 = self.bias_variable([256])
            t_W3 = self.weight_variable([256, self.action_dim])
            t_b3 = self.bias_variable([self.action_dim])
            t_h_conv1 = tf.nn.relu(self.conv2d(self.state_input, t_W_conv1) + t_b_conv1)   
            t_h_pool1 = self.max_pool_2x2(t_h_conv1)    
            t_h_conv2 = tf.nn.relu(self.conv2d(t_h_pool1, t_W_conv2) + t_b_conv2)
            t_h_pool2 = self.max_pool_2x2(t_h_conv2) 
            t_h_conv2_flat = tf.reshape(t_h_pool2, [-1,int((self.state_w/4) * (self.state_h/4) * 64)])
            t_h_layer_one = tf.nn.relu(tf.matmul(t_h_conv2_flat, t_W1) + t_b1)
            t_h_layer_one = tf.nn.dropout(t_h_layer_one, 1)
            t_h_layer_two = tf.nn.relu(tf.matmul(t_h_layer_one, t_W2) + t_b2)
            t_h_layer_two = tf.nn.dropout(t_h_layer_two, 1)
            target_Q_value = tf.matmul(t_h_layer_two, t_W3) + t_b3
            self.target_Q_value = tf.nn.dropout(target_Q_value, 1)
        e_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='current_net')
        t_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='target_net')
        with tf.variable_scope('soft_replacement'):
            self.target_replace_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)]

def create_updating_method(self):
        self.action_input = tf.placeholder("float", [None, self.action_dim])
        self.y_input = tf.placeholder("float", [None])
        Q_action = tf.reduce_sum(tf.multiply(self.Q_value, self.action_input), reduction_indices=1)
        self.cost = tf.reduce_mean(tf.square(self.y_input - Q_action))
        tf.summary.scalar('loss',self.cost)
        with tf.name_scope('train_loss'):
            self.optimizer = tf.train.AdamOptimizer(0.001).minimize(self.cost)

由于篇幅原因，这里不展示所有的代码，有关DQN的各种实际操作有兴趣的同学可以亲自动手尝试。

AC框架的部分代码

AC框架与DQN最大的不同在于，DQN虽然有着两个网络结构（Target Net与Policy Net）但我们实际进行训练时只会对Policy Net进行训练，Target Net的更新方法主要是每隔几步获取一次Policy Net的参数。但在AC框架中，我们需要对Actor与Critic网络同时进行训练与更新，这就使得AC框架的训练时间更长。

def create_AC_network(self):
        with tf.name_scope('inputs'):
            self.state_input = tf.placeholder("float", [None, self.state_h, self.state_w, 1])
        # 创建Actors
        with tf.variable_scope('Actors_net'):
            W_conv1 = self.weight_variable([5,5,1,32])
            b_conv1 = self.bias_variable([32])
            W_conv2 = self.weight_variable([5,5,32,64])
            b_conv2 = self.bias_variable([64])
            W1 = self.weight_variable([int((self.state_w/4) * (self.state_h/4) * 64), 512])
            b1 = self.bias_variable([512])
            W2 = self.weight_variable([512, 256])
            b2 = self.bias_variable([256])
            W3 = self.weight_variable([256, self.action_dim])
            b3 = self.bias_variable([self.action_dim])
            h_conv1 = tf.nn.relu(self.conv2d(self.state_input, W_conv1) + b_conv1)   
            h_pool1 = self.max_pool_2x2(h_conv1)    
            h_conv2 = tf.nn.relu(self.conv2d(h_pool1, W_conv2) + b_conv2) 
            h_pool2 = self.max_pool_2x2(h_conv2) 
            h_conv2_flat = tf.reshape(h_pool2, [-1,int((self.state_w/4) * (self.state_h/4) * 64)])
            h_layer_one = tf.nn.relu(tf.matmul(h_conv2_flat, W1) + b1)
            h_layer_one = tf.nn.dropout(h_layer_one, 1)
            h_layer_two = tf.nn.relu(tf.matmul(h_layer_one, W2) + b2)            
            h_layer_two = tf.nn.dropout(h_layer_two, 1)
            # the output of current_net
            Cai = tf.matmul(h_layer_two, W3) + b3
            # 注意，AC与DQN最大的不同在于，AC是纯随机策略，所以我们的Actors网络与DQN网络最大的不同就在于，我们输出的是行动的概率，而不是具体的动作值函数
            self.acts_prob = tf.nn.softmax(Cai)
            
        
        # third, create the Critic_net
        with tf.variable_scope('Critic_net'):
            t_W_conv1 = self.weight_variable([5,5,1,32])
            t_b_conv1 = self.bias_variable([32])
            t_W_conv2 = self.weight_variable([5,5,32,64])
            t_b_conv2 = self.bias_variable([64])
            t_W1 = self.weight_variable([int((self.state_w/4) * (self.state_h/4) * 64), 512])
            t_b1 = self.bias_variable([512])
            t_W2 = self.weight_variable([512, 256])
            t_b2 = self.bias_variable([256])
            t_W3 = self.weight_variable([256, self.action_dim])
            t_b3 = self.bias_variable([self.action_dim])
            t_W4 = self.weight_variable([self.action_dim , 1])
            t_b4 = self.bias_variable([1])
            t_h_conv1 = tf.nn.relu(self.conv2d(self.state_input, t_W_conv1) + t_b_conv1)   
            t_h_pool1 = self.max_pool_2x2(t_h_conv1)    
            t_h_conv2 = tf.nn.relu(self.conv2d(t_h_pool1, t_W_conv2) + t_b_conv2)
            t_h_pool2 = self.max_pool_2x2(t_h_conv2) 
            t_h_conv2_flat = tf.reshape(t_h_pool2, [-1,int((self.state_w/4) * (self.state_h/4) * 64)])
            t_h_layer_one = tf.nn.relu(tf.matmul(t_h_conv2_flat, t_W1) + t_b1)
            t_h_layer_one = tf.nn.dropout(t_h_layer_one, 1)
            t_h_layer_two = tf.nn.relu(tf.matmul(t_h_layer_one, t_W2) + t_b2)
            t_h_layer_two = tf.nn.dropout(t_h_layer_two, 1)
            Yikuzo_Sekiro = tf.matmul(t_h_layer_two, t_W3) + t_b3
            Yikuzo_Sekiro = tf.nn.dropout(Yikuzo_Sekiro, 1)
            #最后一个全连接层输出的是值函数（犹豫就会败北）
            self.target_V_value = tf.matmul(Yikuzo_Sekiro, t_W4) + t_b4
        e_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Actors_net')
        # Critic_net的参数集
        t_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Critic_net')
        # 这里原本是target_net获取current_net参数的操作，但我们是AC，不需要
    # Critic_net参数的更新方式
    def create_C_updating_method(self):
        # 在DQN中，我们可以将AC中的Critic类比为DQN中起“指导”作用的target，但不同的是，target需要对该动作进行评价，但Critic表面上是对动作评价，实际是根据状态计算TD-error
        #self.action_input = tf.placeholder("float", [None, self.action_dim])
        # this the TD aim value
        self.y_input_ = tf.placeholder("float", [None])
        # this the action's Q_value
        #Q_action = tf.reduce_sum(tf.multiply(self.Q_value, self.action_input), reduction_indices=1)
        # 生成的Q_value实际上是一个action大小的list,action_input是一个one-hot向量,
        # 两者相乘实际上是取出了执行操作的Q值进行单独更新
        # this is the lost
        self.cost = tf.reduce_mean(tf.square(self.y_input_ - 0.5 * self.target_V_value))
        # 均方差损失函数
        # drawing loss graph
        tf.summary.scalar('loss1',self.cost)
        # loss graph save
        with tf.name_scope('train_loss'):
            # use the loss to optimize the network
            self.optimizer1 = tf.train.AdamOptimizer(0.0005).minimize(self.cost)
            # learning_rate=0.0005
    

    #Actors_net的参数更新方式
    def create_A_updating_method(self):
        # 在DQN中，我们可以将AC中的Actors类比为DQN中起“行为”作用的current，但不同的是，current输出的是动作状态值，而Actors输出的是做每个动作的概率
        # action_input是一个one-hot向量
        self.action_input = tf.placeholder("float", [None, self.action_dim])
        # this the TD aim value
        self.y_input = tf.placeholder("float", [None])
        # 下面是AC算法的Actors更新过程，不论是书上还是帖子上的都差不多，依葫芦画瓢而已XD
        log_prob = tf.log(tf.reduce_mean(tf.multiply(self.acts_prob , self.action_input) , axis = 1 , keep_dims = False))
        TDERROR = self.y_input - 0.5 * self.target_V_value
        self.exp_v = tf.reduce_mean(log_prob * TDERROR)
        tf.summary.scalar('loss2',self.exp_v)
        # loss graph save
        with tf.name_scope('train_loss'):
            # use the loss to optimize the network
            self.optimizer2 = tf.train.AdamOptimizer(0.0000000001).minimize(-self.exp_v)
            # learning_rate=0.0001,按道理说，Actors的学习能力与水平应该比Critic差一点

上面是AC框架的部分代码，主要是将DQN的代码基于AC框架的原理进行修改后得到，有关具体的区别，本文也不多加赘述。

我们将上面所说的所有方法整合，并用DQN与AC框架两种不同的方法游玩《只狼》与《黑暗之魂二原罪学者》，最终发现了一个很有趣的事实：在面对不同的boss时，DQN通过训练往往能够达到较好的表现，而AC框架在应对不同的普通敌人以及精英敌人时，表现得比DQN更好。

原文链接：https://blog.csdn.net/qq_63040955/article/details/122718038

AC框架与DQN在《只狼》以及《黑暗之魂》中的应用

前言：