Andrew Ng机器学习（五）Logistic回归练习——二分类练习

1、基础内容

（1）公式总结:

（2）内容回归:

逻辑回归主要用于二分类和多分类。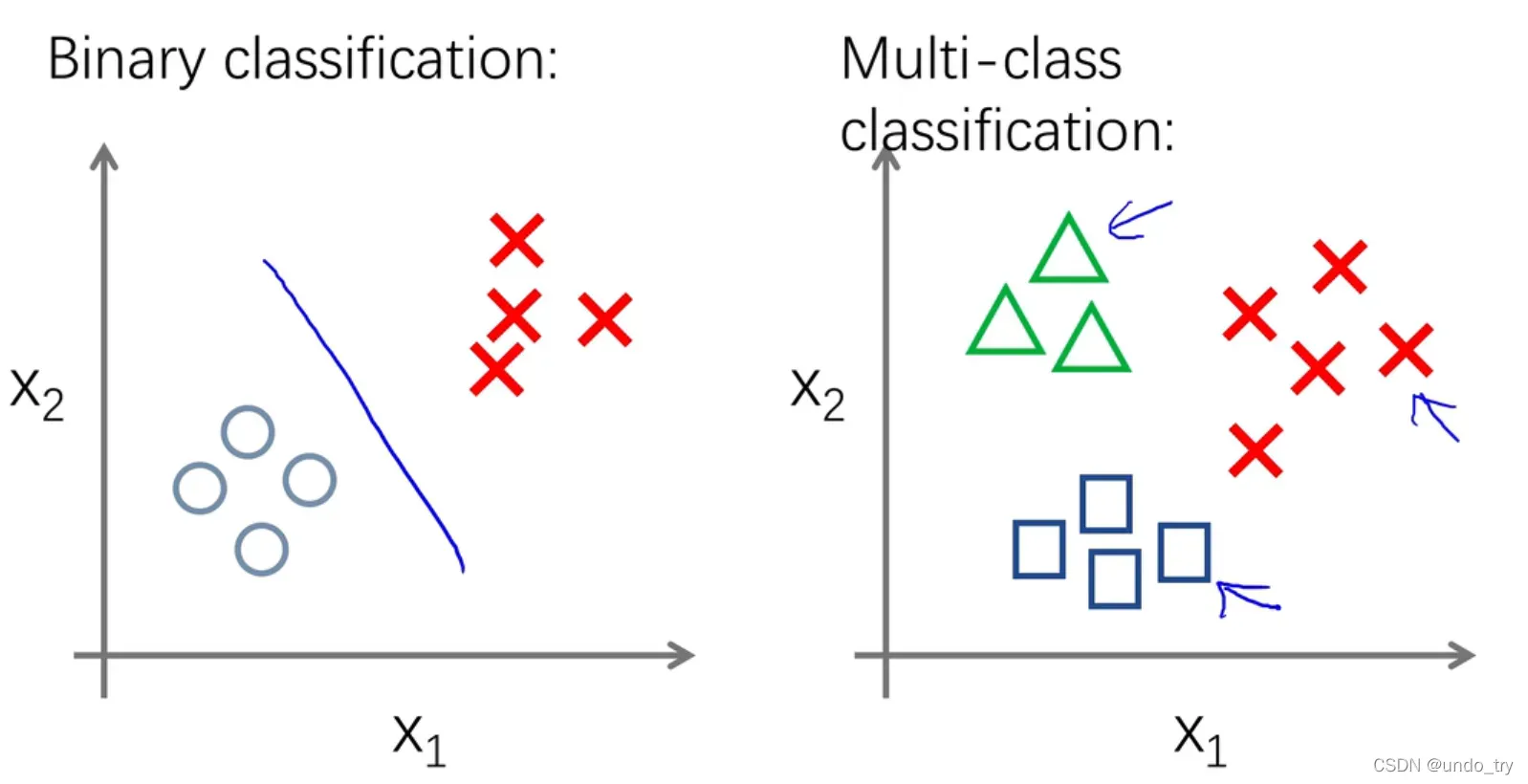
在二元分类中，分为线性可分和线性不可分。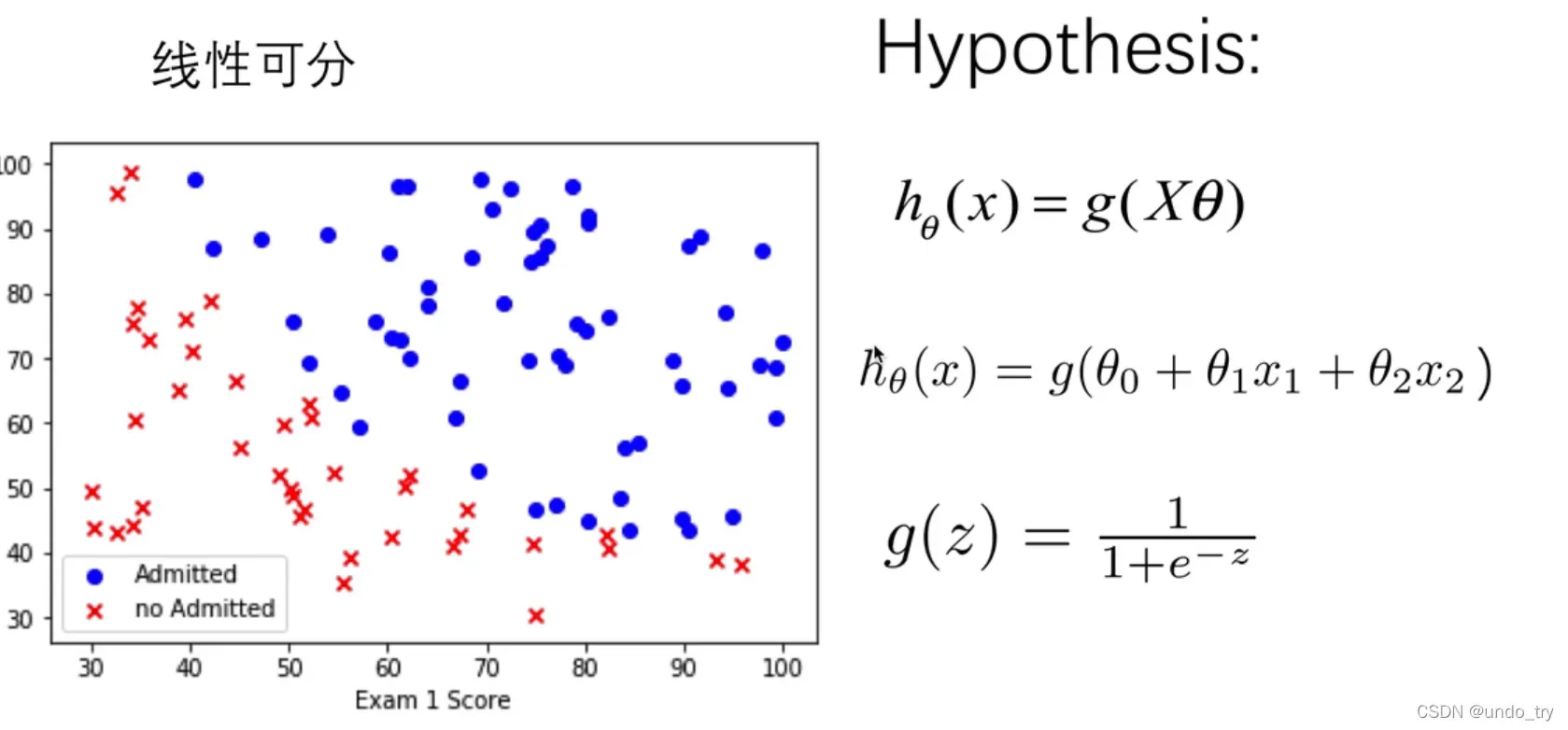


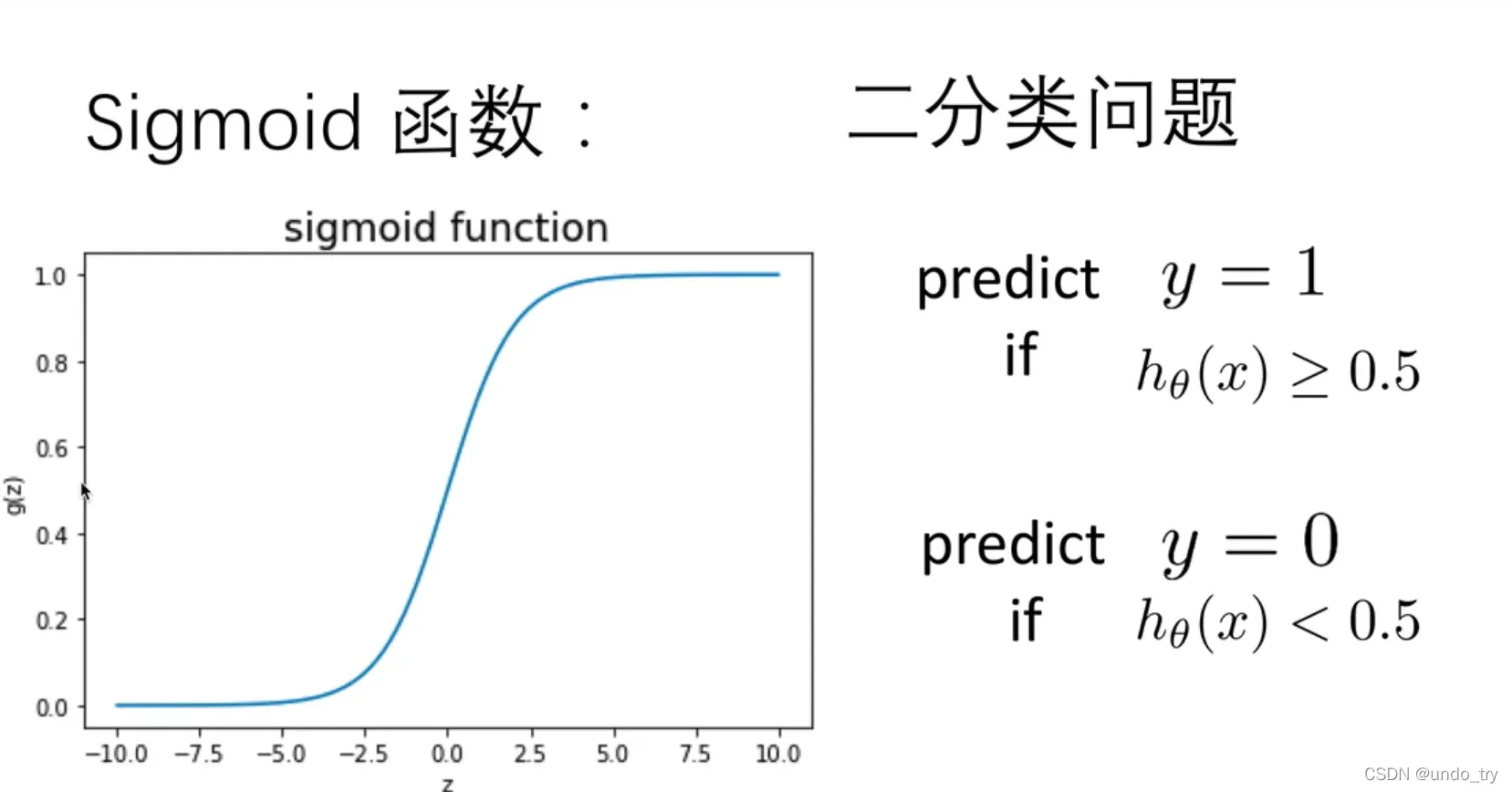
对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convexfunction）。

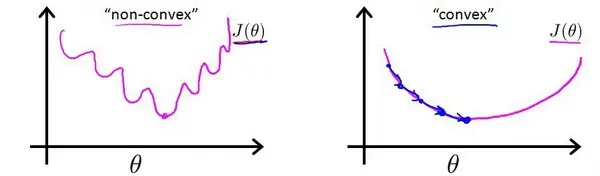
这意味着我们的成本函数有很多局部最小值，这会影响梯度下降算法找到全局最小值。

线性回归的代价函数为：。
我们将逻辑回归的成本函数重新定义为：，其中

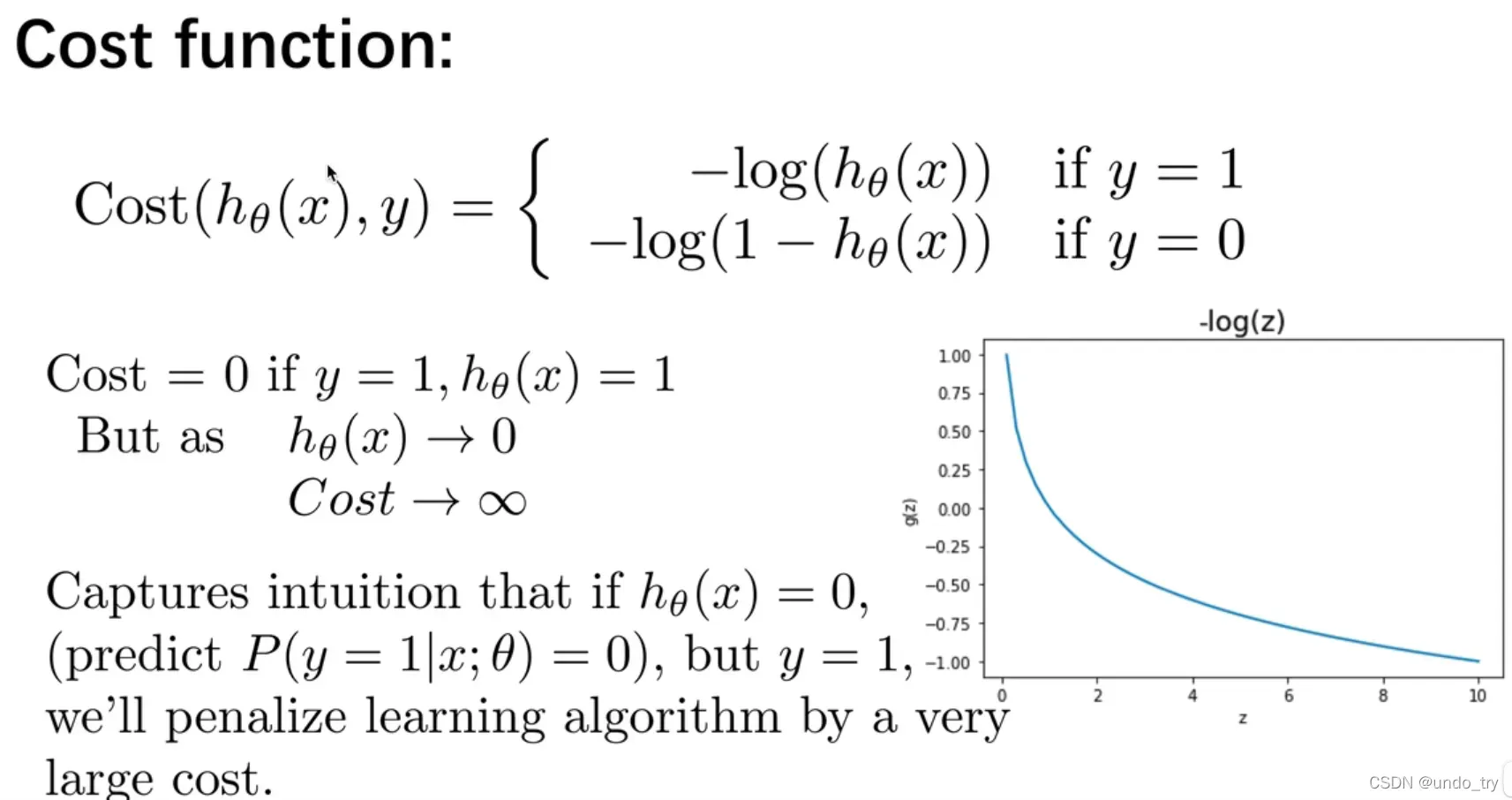
和的关系如下图所示：

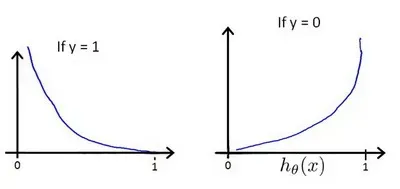
这样构建的函数的特点是：当实际的且也为 1 时误差为 0，当但不为1时误差随着变小而变大；当实际的且也为 0 时代价为 0，当但不为 0时误差随着的变大而变大。
将构造的 简化如下：

引入代价函数得到：

即：

执行矢量化表示；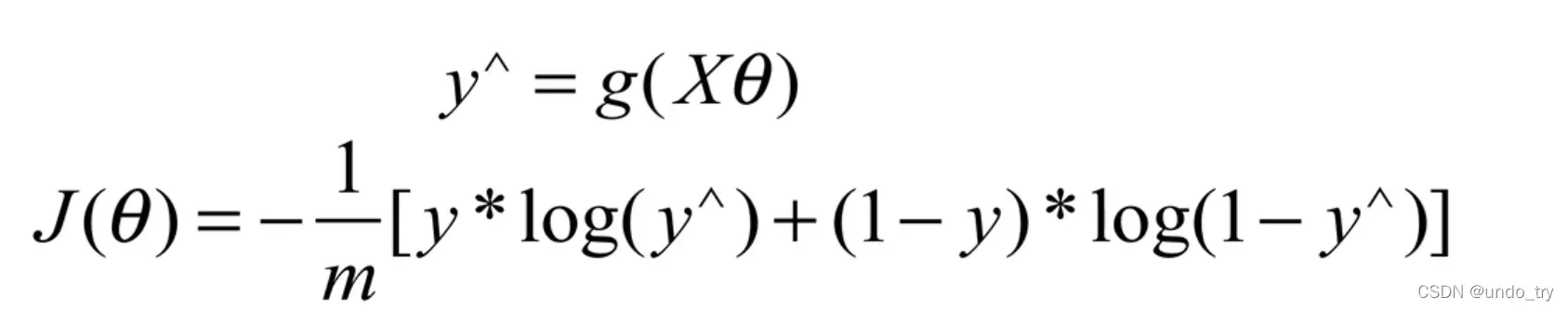

梯度下降的工作方式与线性回归相同：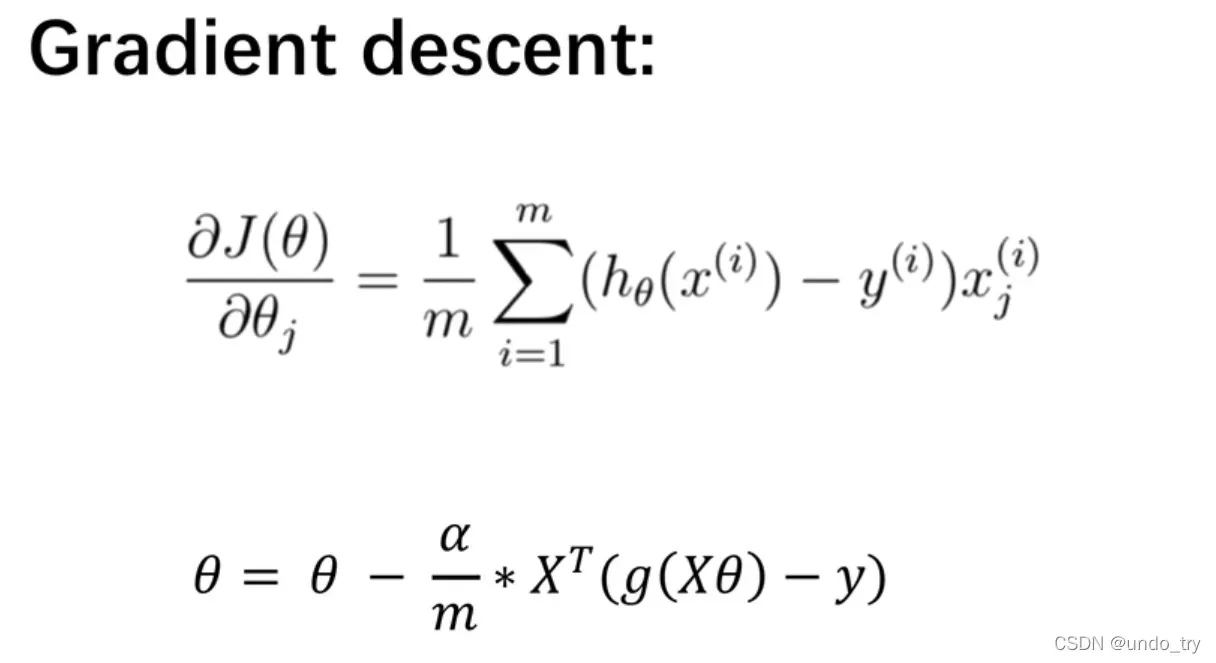

2、二分类案例(线性可分)___依据两次测试的成绩，预测是否被大学录取

（1）读取数据、绘制图像

"""
  二分类案例:
  依据两次测试的成绩，预测是否被大学录取
"""
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 1、读取数据
# 读取数据
df = pd.read_csv('ex2data1.txt',header=None,names=['exam1','exam2','accepted'])
print(df.head())
#        exam1      exam2  accepted
# 0  34.623660  78.024693         0
# 1  30.286711  43.894998         0
# 2  35.847409  72.902198         0
# 3  60.182599  86.308552         1
# 4  79.032736  75.344376         1

# 2、绘制图像
# 绘图
fig,ax = plt.subplots()
ax.scatter(df[df['accepted'] == 0]['exam1'],df[df['accepted'] == 0]['exam2'],c = 'red',marker='x' ,label='y=0')
ax.scatter(df[df['accepted'] == 1]['exam1'],df[df['accepted'] == 1]['exam2'],c = 'green',marker='o',label='y=1' )
ax.legend()
ax.set(xlabel='exam1',ylabel='exam2',title='Fig')
plt.show()

可以看到一个二元分类问题。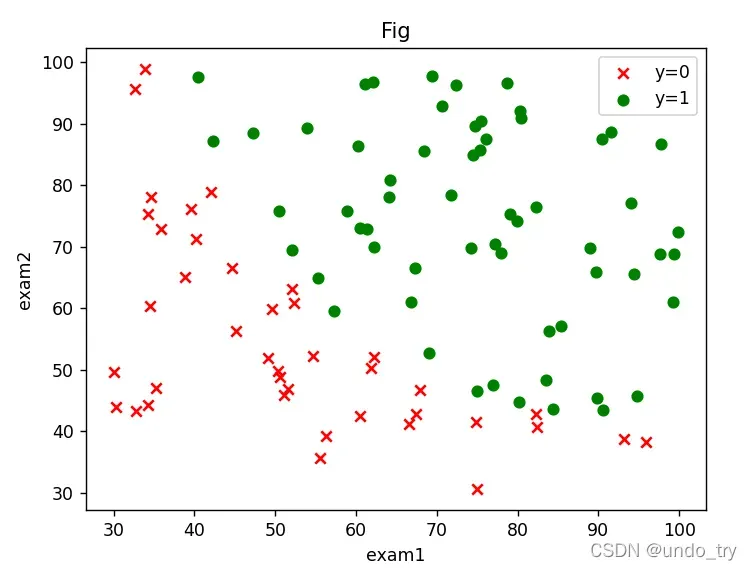

(2)计算theta_final

# 3、从数据集中切分出X和y
def getX_y(df):
    # 添加一列
    df.insert(0,'const',1)
    # 切出X 以及 y
    X = df.iloc[:,0:-1]
    y = df.iloc[:, -1]

    # 将X  和 y转换为数组的形式
    X = X.values
    y = y.values
    y = y.reshape(len(y),1)
    return X,y

X,y = getX_y(df)
# 定义激活函数
def sigmod(z):
    return 1 / (1 + np.exp(-z))

# 定义costFunction
def costFunction(X, y, theta):
    A = sigmod(X @ theta)
    first = y * np.log(A)
    second = (1 - y) * np.log(1 - A)
    return -np.sum(first + second) / len(y)




# 定义梯度下降函数
def gradientDescent(X, y, theta, alpha, iters):
    costs = []
    for i in range(iters):
        A = sigmod(X @ theta)
        theta = theta - (alpha * X.T @ (A - y)) / (len(y))
        cost = costFunction(X, y, theta)
        costs.append(cost)

        if i % 1000 == 0:
            print(cost)
    return theta, costs

alpha = 0.004
iters = 200000
# 初始化theta
theta = np.zeros((3,1))

theta_final,costs = gradientDescent(X,y,theta,alpha,iters)
print(theta_final)

（3）计算预测准确率，绘制决策边界

# 定义预测函数
def predict(X, theta):
    p = sigmod(X @ theta)
    return [1 if x >= 0.5 else 0 for x in p]

# 计算预测的准确性
y_ = np.array(predict(X,theta_final))
y_pre = y_.reshape(len(y_),1)
acc = np.mean(y_pre == y)
print(acc)  # 0.91


# 绘制决策边界
x = np.linspace(20,100,100)
f = - theta_final[0,0] / theta_final[2,0] - theta_final[1,0] / theta_final[2,0] * x

# 绘图
fig,ax = plt.subplots()
ax.scatter(df[df['accepted'] == 0]['exam1'],df[df['accepted'] == 0]['exam2'],c = 'red',marker='x' ,label='y=0')
ax.scatter(df[df['accepted'] == 1]['exam1'],df[df['accepted'] == 1]['exam2'],c = 'green',marker='o',label='y=1' )
ax.plot(x,f,c = 'blue',label='border' )
ax.legend()
ax.set(xlabel='exam1',ylabel='exam2',title='Fig')
plt.show()

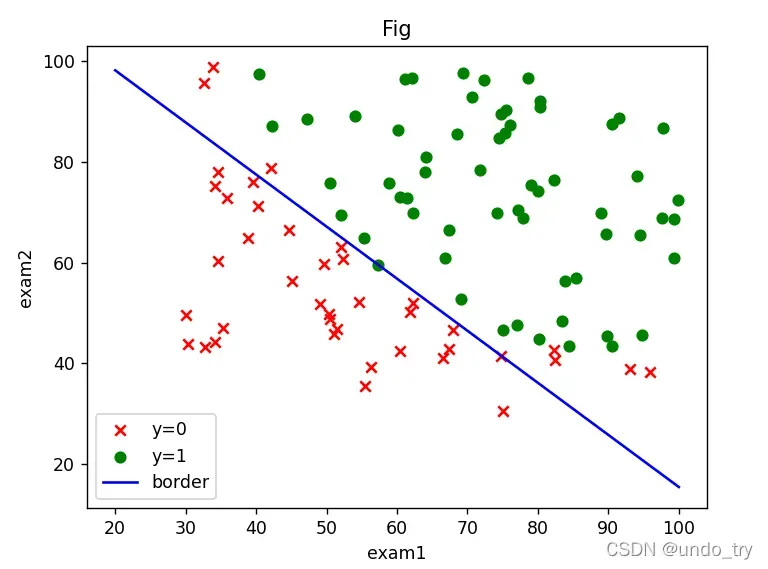
3、二分类案例(线性不可分)___依据两次测试的成绩，决定芯片要被抛弃还是接受

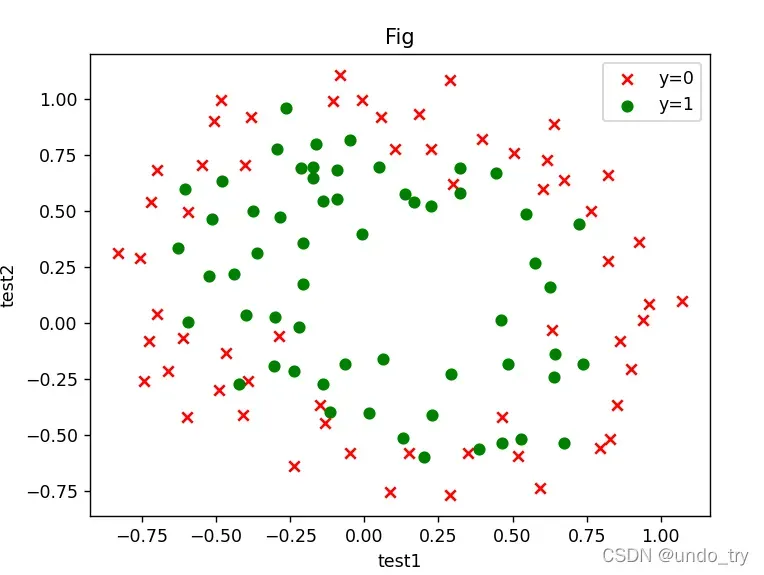
没有办法用直线切片。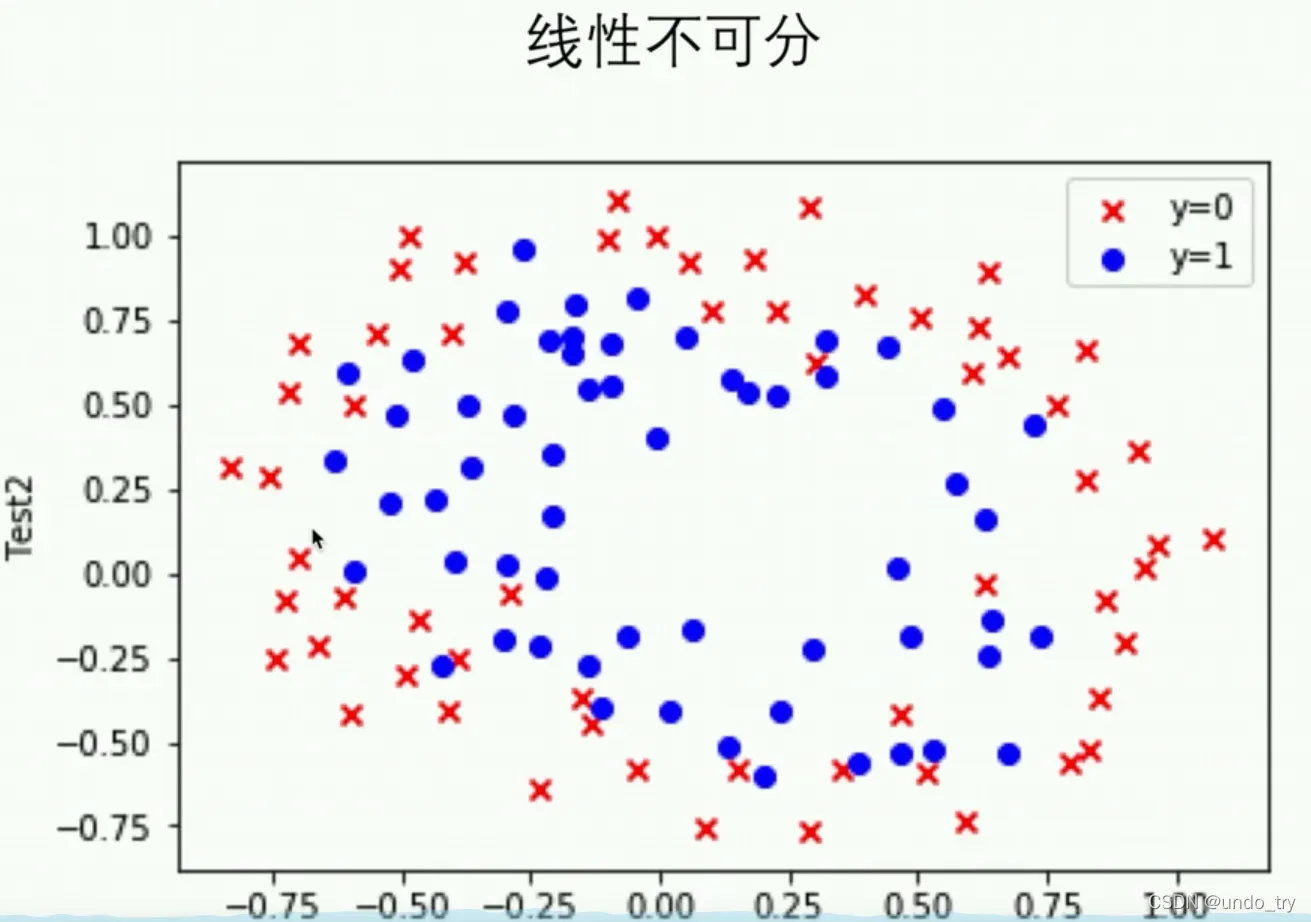

需要特征图：

为了防止过拟合，需要添加一个正则项：


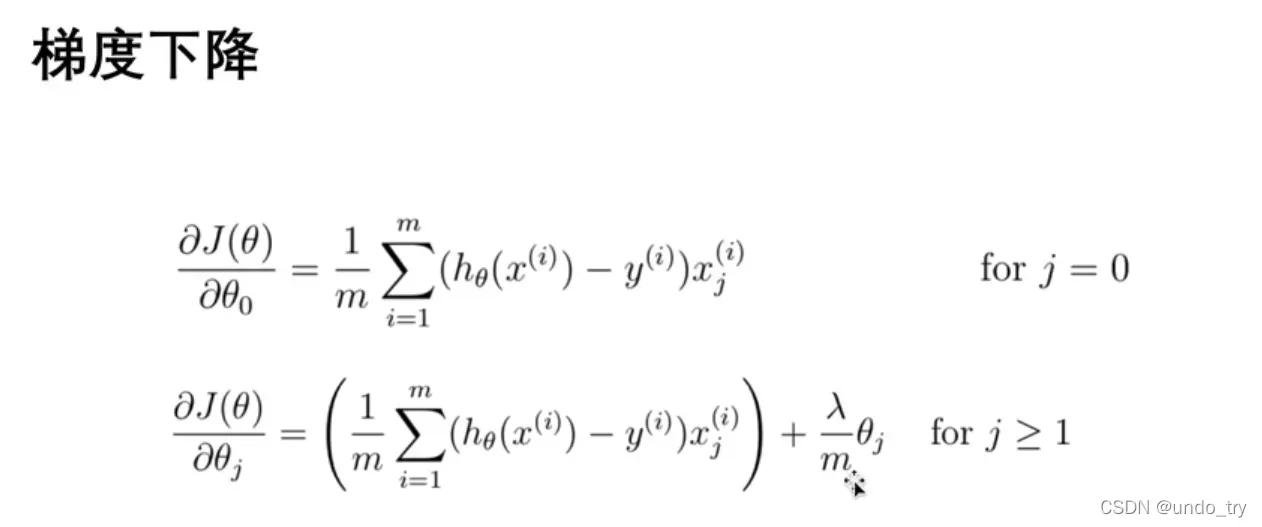
(1)读取原始数据，画图

"""
  逻辑回归练习（线性不可分）:
    决定芯片要被抛弃还是接受
    数据集： 芯片在两次测试中的测试结果
"""
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 读取数据
df = pd.read_csv('ex2data2.txt',header=None,names=['test1','test2','accepted'])
print(df.head())

#       test1    test2  accepted
# 0  0.051267  0.69956         1
# 1 -0.092742  0.68494         1
# 2 -0.213710  0.69225         1
# 3 -0.375000  0.50219         1
# 4 -0.513250  0.46564         1



# 绘图
fig,ax = plt.subplots()
ax.scatter(df[df['accepted'] == 0]['test1'],df[df['accepted'] == 0]['test2'],c = 'red',marker='x' ,label='y=0')
ax.scatter(df[df['accepted'] == 1]['test1'],df[df['accepted'] == 1]['test2'],c = 'green',marker='o',label='y=1' )
ax.legend()
ax.set(xlabel='test1',ylabel='test2',title='Fig')
plt.show()

(2)使用特征映射，定义函数计算theta

# 线性不可分，用特征映射
def feature_mapping(x1, x2, power):
    data = {}
    for i in np.arange(power + 1):
        for j in np.arange(i + 1):
            data['F{}{}'.format(i - j, j)] = np.power(x1, i - j) * np.power(x2, j)
    return pd.DataFrame(data)
x1 = df['test1']
x2 = df['test2']

mdf = feature_mapping(x1,x2,6)
# 从两个数据集中切分别分出X和y
# 切出X 以及 y
y = df.iloc[:, -1]
# 将X  和 y转换为数组的形式
X = mdf.values
y = y.values
y = y.reshape(len(y),1)
# 定义激活函数
def sigmod(z):
    return 1 / (1 + np.exp(-z))

# 定义costFunction
def costFunction(X, y, theta, lamda):
    A = sigmod(X @ theta)
    first = y * np.log(A)
    second = (1 - y) * np.log(1 - A)
    #加入正则化项
    reg = np.sum( np.power(theta[1:],2) ) * (lamda / (2 * len(y)) )
    return -np.sum(first + second) / len(y) + reg


# 定义梯度下降函数
def gradientDescent(X, y, theta, alpha, iters, lamda):
    costs = []
    for i in range(iters):
        reg = theta[1:] * (lamda / len(y))
        reg = np.insert(reg, 0, values=0, axis=0)

        A = sigmod(X @ theta)
        theta = theta - (alpha * X.T @ (A - y)) / (len(y)) - alpha * reg
        cost = costFunction(X, y, theta, lamda)
        costs.append(cost)
        if i % 1000 == 0:
            print(cost)
    return theta, costs
# 初始化参数
alpha = 0.001
iters = 20000
# lamda = 0.001
lamda = 0.0001
theta = np.zeros((28,1))
# 计算
theta_final,costs = gradientDescent(X,y,theta,alpha,iters,lamda)
print(theta_final)

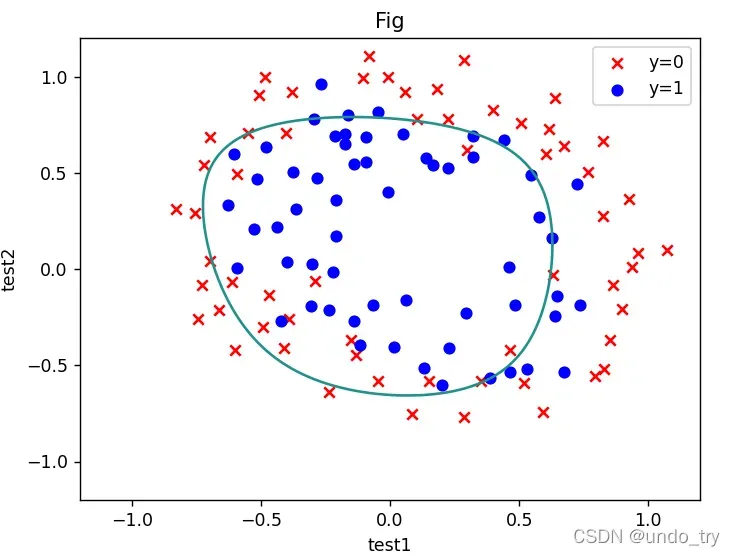
(3)计算预测准确率，画出决策边界

# 定义预测函数
def predict(X, theta):
    p = sigmod(X @ theta)

    return [1 if x >= 0.5 else 0 for x in p]
# 计算预测的准确性
y_ = np.array(predict(X,theta_final))
y_pre = y_.reshape(len(y_),1)
acc = np.mean(y_pre == y)
print(acc) # 0.7796610169491526

# 绘制决策边界
x = np.linspace(-1.2,1.2,200)
xx,yy = np.meshgrid(x,x)
print(xx.shape)
z = feature_mapping(xx.ravel(),yy.ravel(),6).values
zz = z @ theta_final
zz = zz.reshape(200,200)

fig,ax = plt.subplots()
ax.scatter(df[df['accepted'] == 0]['test1'],df[df['accepted'] == 0]['test2'],c = 'red',marker='x' ,label='y=0')
ax.scatter(df[df['accepted'] == 1]['test1'],df[df['accepted'] == 1]['test2'],c = 'blue',marker='o',label='y=1' )
ax.legend()
ax.set(xlabel='test1',ylabel='test2',title='Fig')
plt.contour(xx,yy,zz,0)
plt.show()