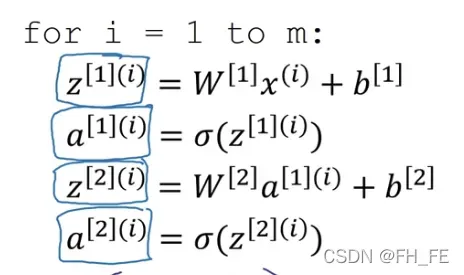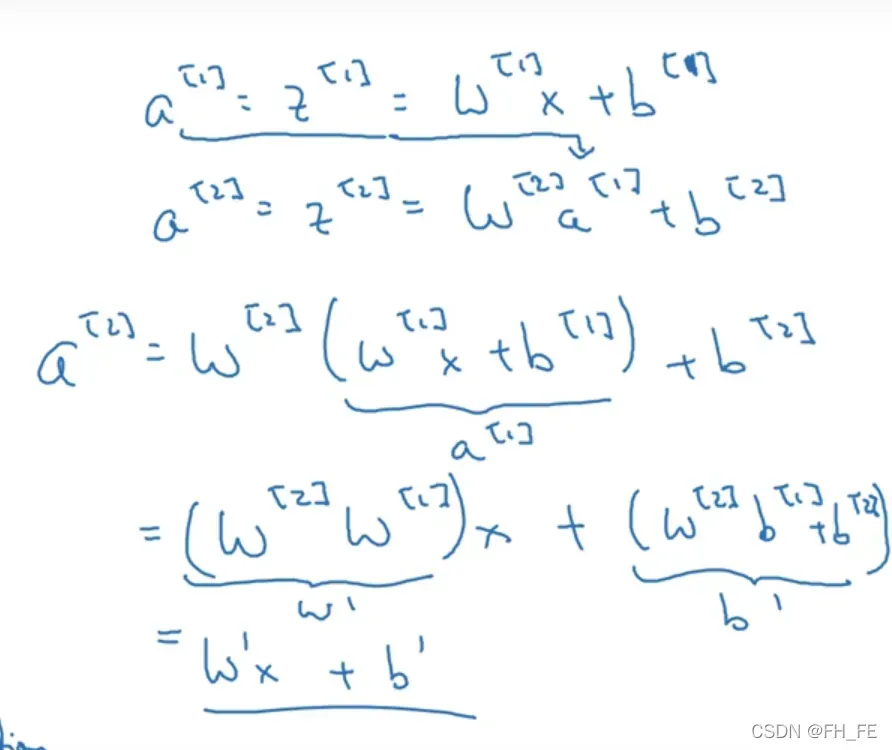神经网络

3.1 神经网络的结构

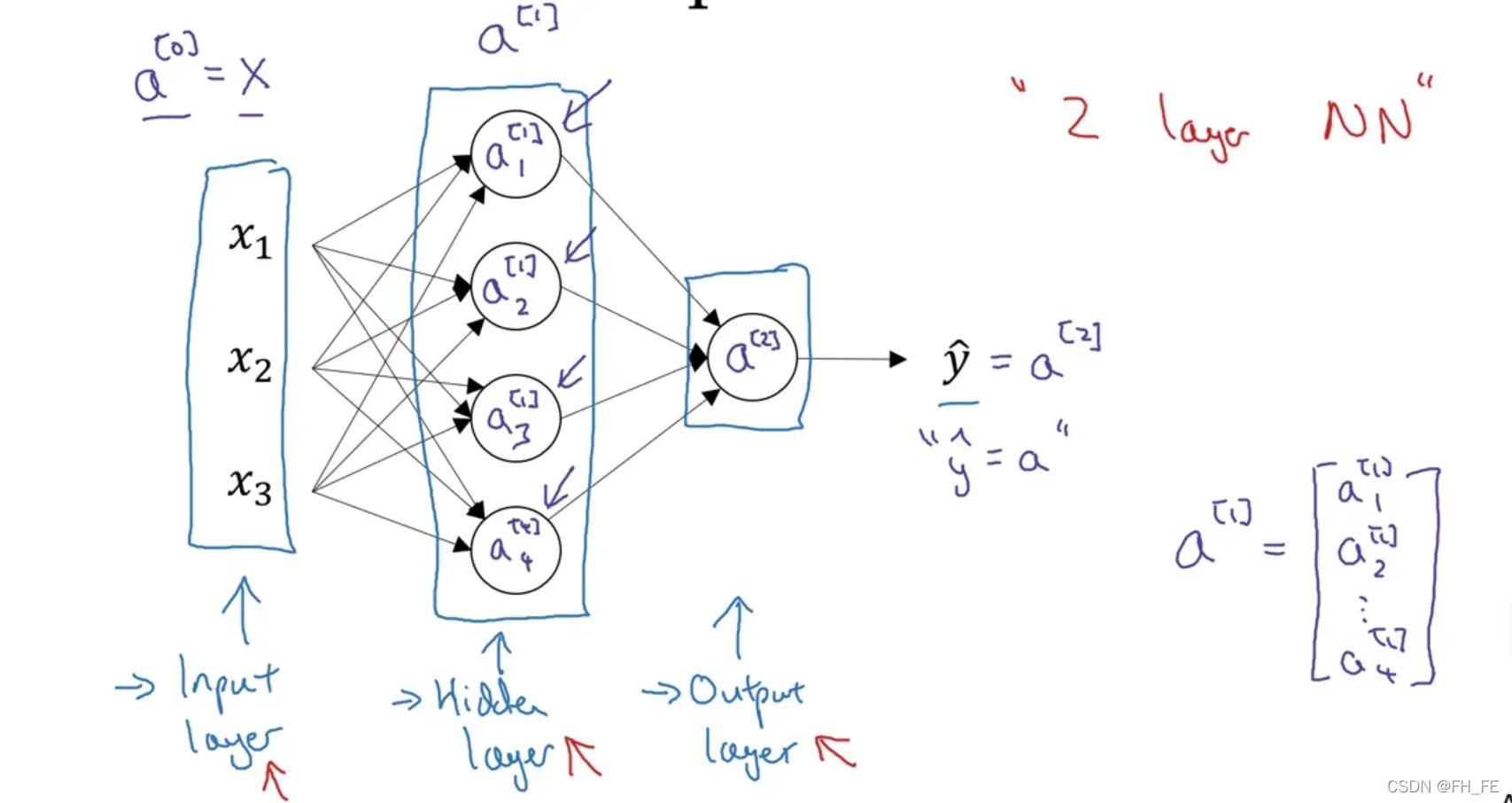
表示方法

用圆括号表示网络中的单个元素
用方括号表示网络中的层，每一层中的各个元素用下标表示
输入层为第 0 层

结构

一个网络分为 ：

1. 输入层 a[0]
2. 隐层
3. 输出层
   如上图，是一个两层网络模型，一般认为输入层不是一个标准神经网络层

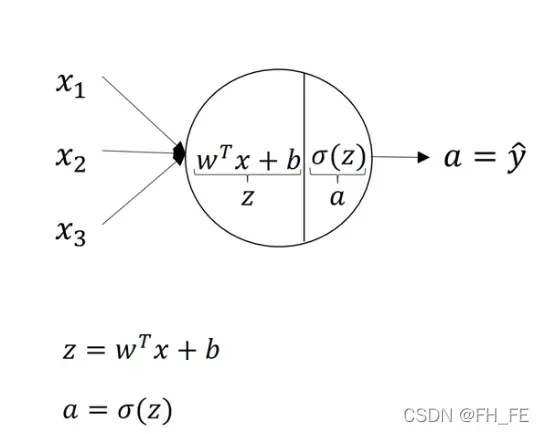
3.2 神经网络的输出

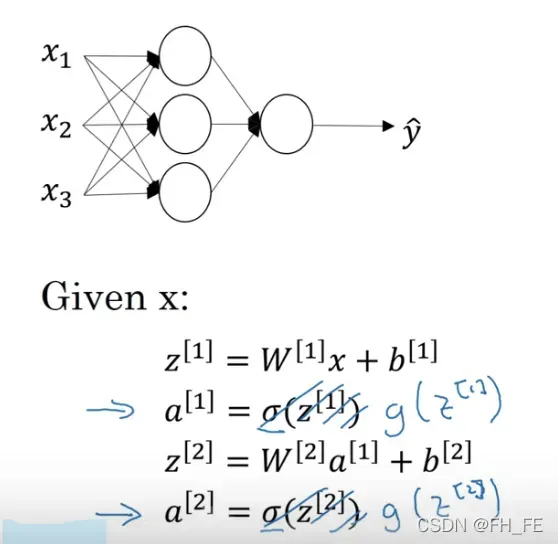
对于每个隐层的结点单元，我们要分别算出其 z 值与 sigmoid(z)

对每一层的每个结点进行同样的操作

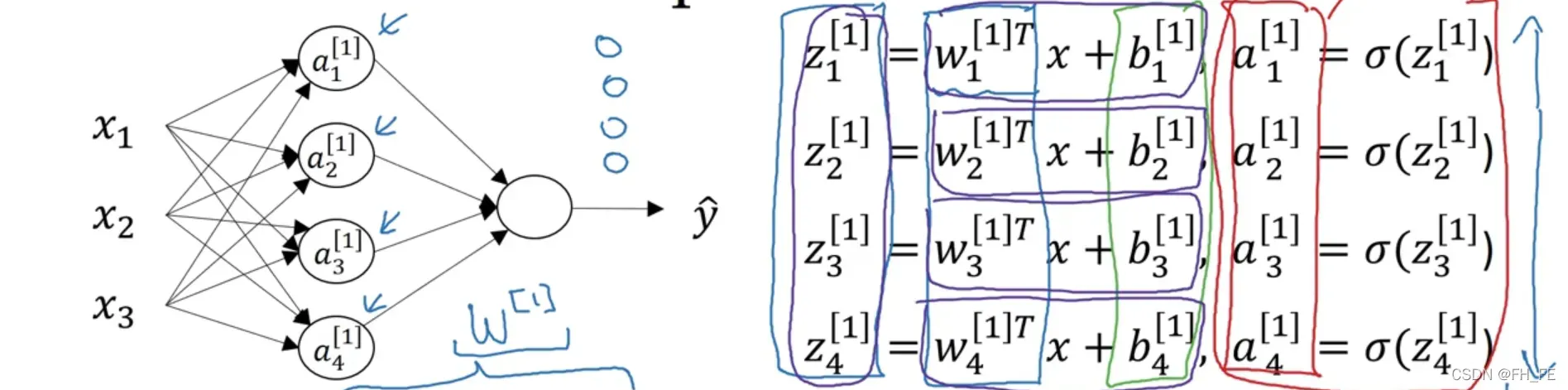
对隐层 z^[1] 的运算如下
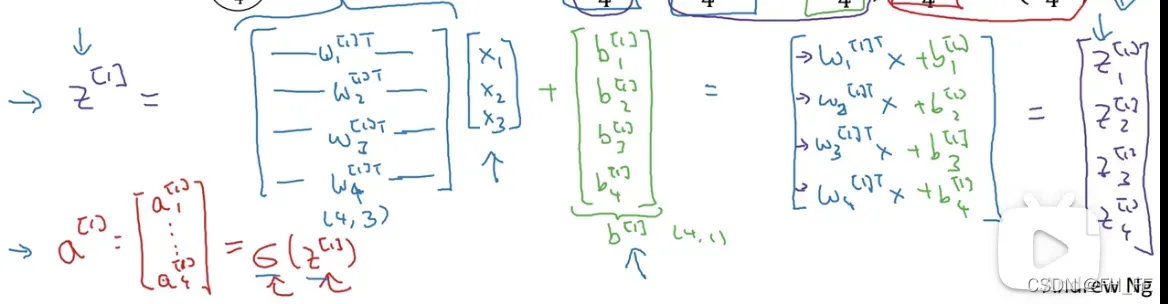
但是该过程如果使用 for 的话效率就很低，于是我们对其进行向量化

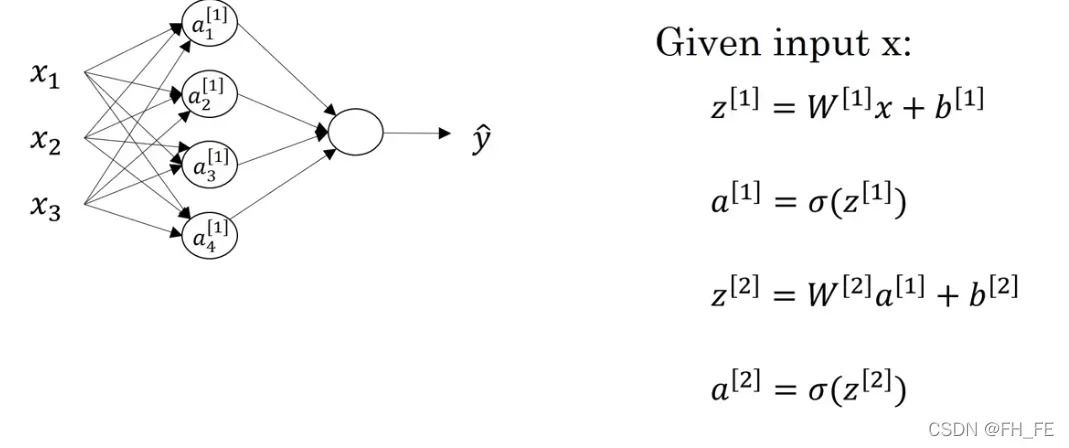
整理得到 对于单个样本

实际上，这个神经网络只需要以上四行代码即可完成计算
对于 m个样本

向量化后

3.3 激活函数

当然可用的激活函数不止 sigmoid 一种，于是神经网络的激活函数可以用 g(z) 表示

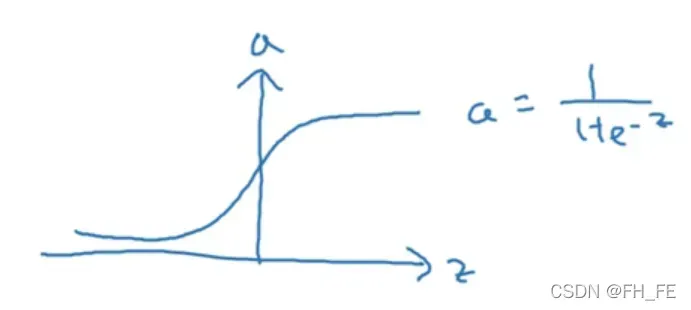
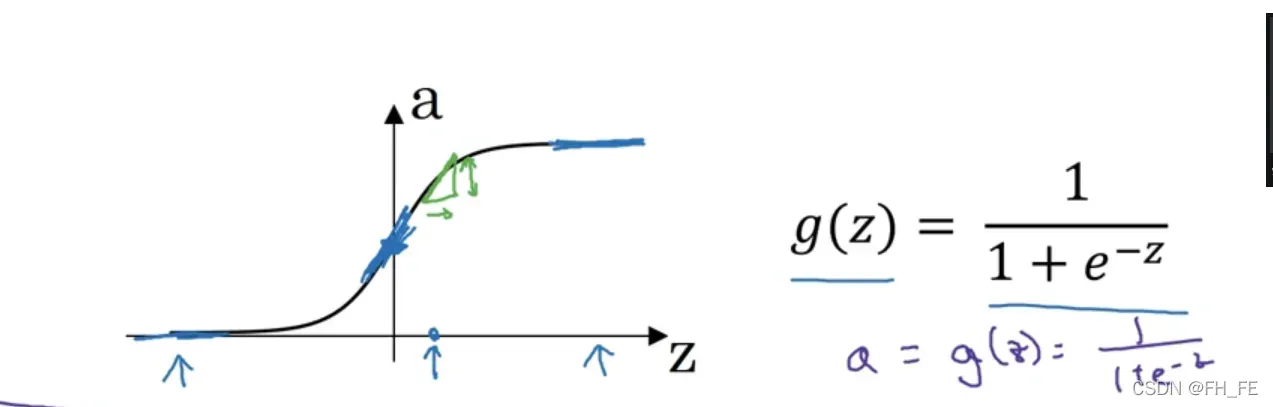
sigmoid
进行二分类时，输出结果要介于 0-1之间，所以此时使用 sigmoid 函数更合适

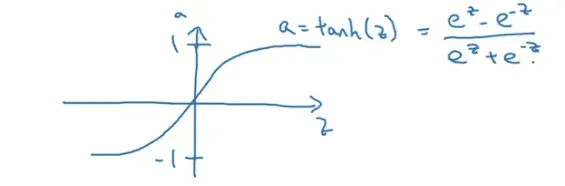
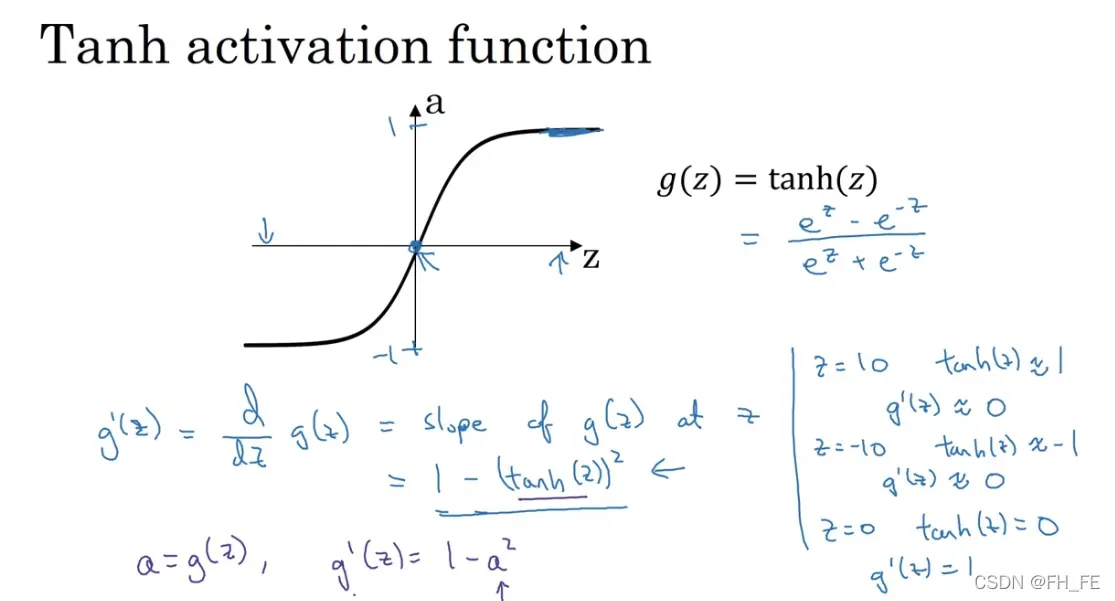
tanh 双曲正切函数
效果往往比 sigmoid 要好，它可以让数据平均值接近 0， 方便下一次数据处理

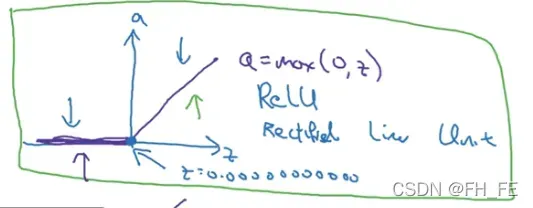
ReLU 修正线性单元
这是机器学习中最受欢迎的一个激活函数，对于前两个激活函数，当 z 值过大或者过小时，斜率接近0，导致梯度下降的速度很慢，而 ReLU 在 z 为正的部分斜率为 1 ，而在 0 处可以选择赋值为 0 或者 1。对于 z 的负值部分，可以使用 泄露ReLU 函数或者不做考虑，因为有足够多的神经元使得 z 的值为正，所以大多数梯度下降的速度很快。
在不知道用什么激活函数的时候一般使用 ReLU

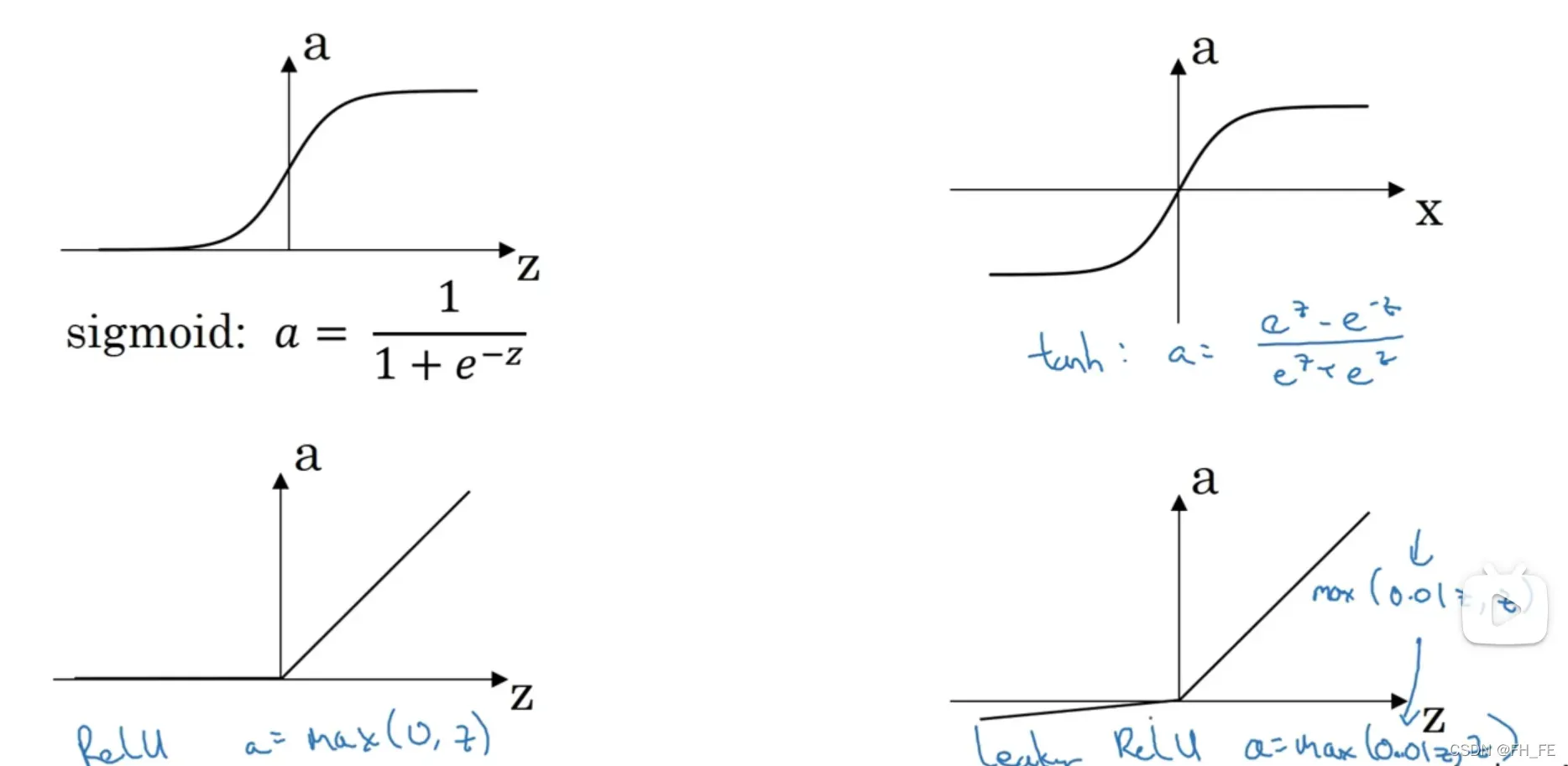
3.4 为什么要使用激活函数呢？

如下图推导过程所示，如果不使用激活函数，那么无论有多少个隐层，最终的计算过程相当于进行了一次线性组合，那么多个隐层就相当于只有一个隐层。

线性隐层毫无意义，所以应该使用非线性的激活函数

线性函数只有在回归问题中使用，比如房价都是正实数，训练用来估计房价的的模型时使用线性函数

3.5 梯度下降法

激活函数的导数

sigmoid

tanh(z)

ReLU

正向传播与反向传播过程

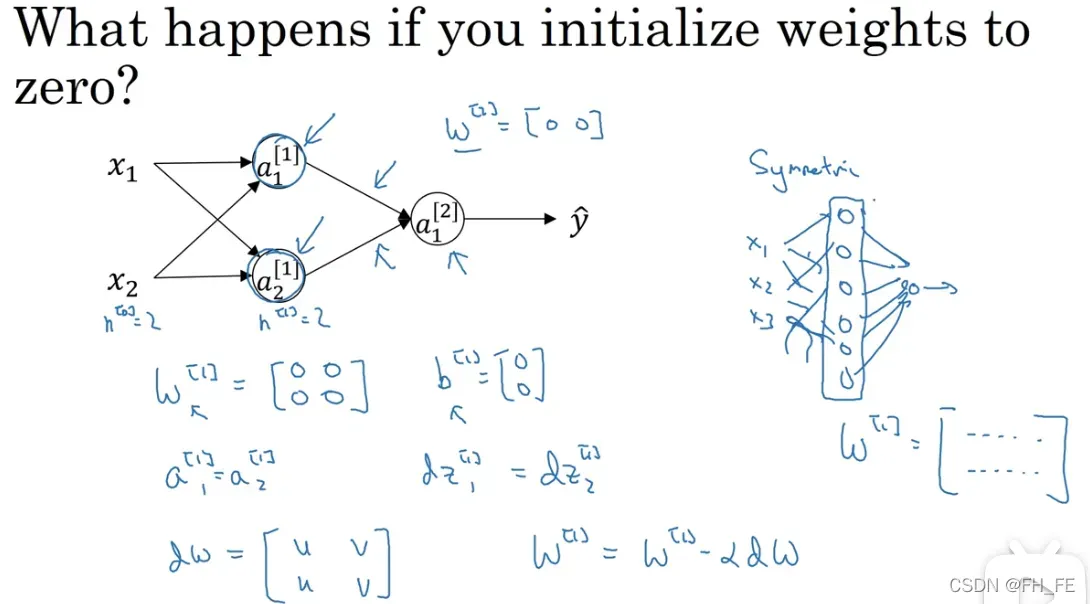
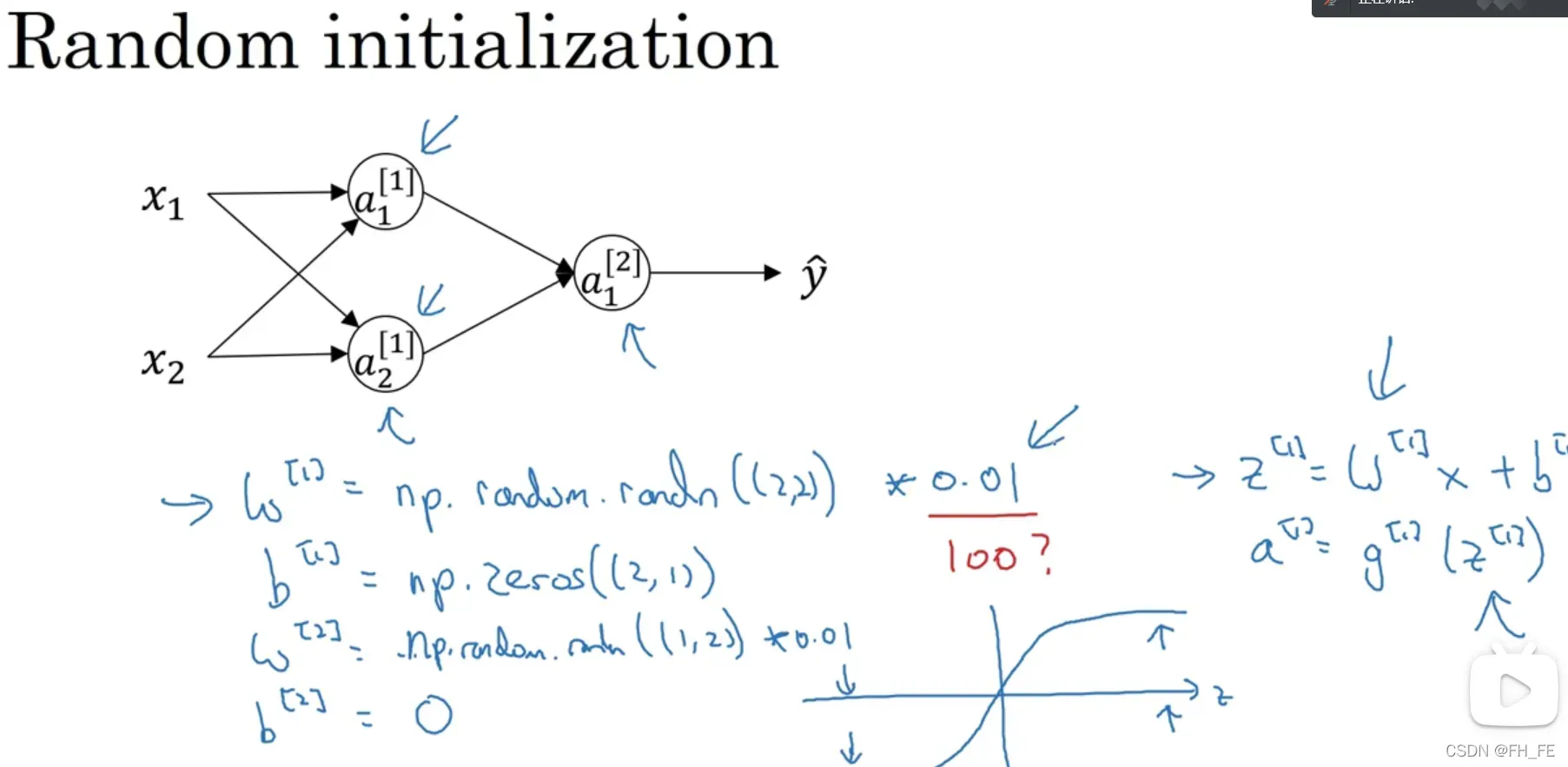
随机初始化权重

如果初始化权重均为 0 ，那么对于每个结点，无论进行多少次梯度下降，其计算结果都是对称的（相同的计算过程），对模型的训练没有用
证明如下

参数的初始化
W的初始化不能全为0，会影响对称性
b的初始化可以为0，不影响对称性
*
初始化 W 为什么要乘 0.01 而不是 100 呢？
这与计算过程有关，W 过大会导致 z 过大，带入激活函数中容易落入斜率趋于 0 的区域，使学习速度大大降低，所以一般会选择乘一个小常数