介绍谱聚类（spectral clustering）

1、谱聚类概览

谱聚类演化于图论，后由于其表现出优秀的性能被广泛应用于聚类中，对比其他无监督聚类（如kmeans），spectral clustering的优点主要有以下：

1.过程对数据结构并没有太多的假设要求，如kmeans则要求数据为凸集。
2.可以通过构造稀疏similarity graph，使得对于更大的数据集表现出明显优于其他算法的计算速度。
3.由于spectral clustering是对图切割处理，不会存在像kmesns聚类时将离散的小簇聚合在一起的情况。
4.无需像GMM一样对数据的概率分布做假设。

同样，spectral clustering也有自己的缺点，主要存在于构图步骤，有如下：

1.对于选择不同的similarity graph比较敏感（如 epsilon-neighborhood， k-nearest neighborhood，fully connected等）。
2.对于参数的选择也比较敏感（如 epsilon-neighborhood的epsilon，k-nearest neighborhood的k，fully connected的 ）。

谱聚类过程主要有两步，第一步是构图，将采样点数据构造成一张网图，表示为G(V,E)，V表示图中的点，E表示点与点之间的边，如下图：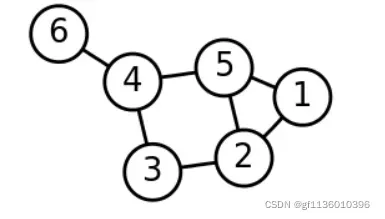
图1 谱聚类构图(来源wiki)

第二步，切图，即将第一步构建的图按照一定的裁剪标准划分为不同的图，不同的子图，也就是我们对应的聚类结果如下：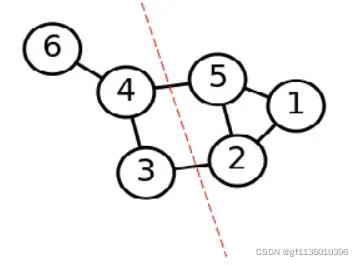
图2 谱聚类切图
一般来说，它的主要思想是把所有的数据看作空间中的点，这些点可以通过边连接起来。距离较远的两点之间的边权值较低，而距离较近的两点之间的边权值较高。子图之间的边权重之和尽可能低，而子图中的边权重之和尽可能高，从而达到聚类的目的。

2、谱聚类构图

一般有以下三种组合：
1. -neighborhood
2. k-nearest neighborhood
3. fully connected
前两种可以构造出稀疏矩阵，适合大样本的项目，第三种则相反，在大样本中其迭代速度会受到影响制约，在讲解三种构图方式前，需要引入similarity function，即计算两个样本点的距离，一般用欧氏距离：, 表示样本点与的距离，或者使用高斯距离，其中 的选取也是对结果有一定影响，其表示为数据分布的分散程度，通过上述两种方式之一即可初步构造矩阵，一般称 为Similarity matrix(相似矩阵)。
对于第一种构图 -neighborhood，顾名思义是取的点，则相似矩阵可以进一步重构为邻接矩阵(adjacency matrix) :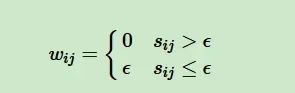

可以看出，在 ε-neighborhood重构下，样本点之间的权重没有包含更多的信息了。
对于第二种构图k-nearest neighborhood，其利用KNN算法，遍历所有的样本点，取每个样本最近的k个点作为近邻，但是这种方法会造成重构之后的邻接矩阵 W非对称，为克服这种问题，一般采取下面两种方法之一：
一是只要点xi在 xj的K个近邻中或者 xj在 xi的K个近邻中，则保留并对其做进一步处理 W，此时 为：

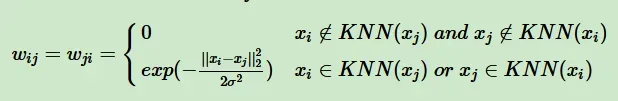
二是必须满足点 在 的K个近邻中且 在 的K个近邻中，才会保留并做进一步变换，此时 W为：
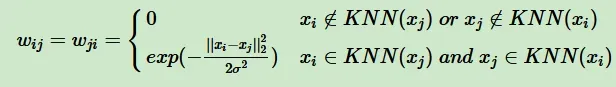对于第三种构图fully connected，一般使用高斯距离：，则重构之后的矩阵 W与之前的相似矩阵SS相同，为：。
在了解三种构图方式后，还需要注意一些细节，对于第一二中构图，一般是重构基于欧氏距离的 ，而第三种构图方式，则是基于高斯距离的 ，注意到高斯距离的计算蕴含了这样一个情况：对于比较大的样本点，其得到的高斯距离反而值是比较小的，而这也正是 S可以直接作为W的原因，主要是为了将距离近的点的边赋予高权重。
得到邻接矩阵 W后，需要做进一步的处理：
(1).计算阶矩(degree matrix)D：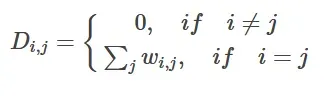

其中其中为邻接矩阵 W元素，表示将图中某点所连接的其他点的边的权重之和，可以看出， D为对角矩阵.
(2).计算拉普拉斯矩阵(Laplacians matrix)L： L=D−W
如此，在构图阶段基本就完成了，至于为什么要计算出拉普拉斯矩阵 LL，可以说L=D−W这种形式对于后面极大化问题是非常有利的。

在实际的应用中，使用第三种全连接法来建立邻接矩阵是最普遍的，而在全连接法中使用高斯径向核RBF是最普遍的。

3、拉普拉斯矩阵

单独把拉普拉斯矩阵(Graph Laplacians)拿出来介绍是因为后面的算法和这个矩阵的性质息息相关。它的定义很简单，拉普拉斯矩阵L=D−W。D即为度矩阵，它是一个对角矩阵。而W拉普拉斯矩阵有一些很好的性质如下：

1）拉普拉斯矩阵是对称矩阵，这可以由D
和W

都是对称矩阵。

2）由于拉普拉斯矩阵是对称矩阵，则它的所有的特征值都是实数。

3）对于任意的向量f,我们有

4、切图聚类

为了避免最小切图导致的切图效果不佳，我们需要对每个子图的规模做出限定，一般来说，有两种切图方式，第一种是RatioCut，第二种是Ncut。下面我们分别加以介绍。

其中 |Ai| 为 Ai中点的个数， vol(Ai)为 Ai中所有边的权重和。

4.1RatioCut

RatioCut切图为了避免第五节的最小切图，对每个切图，不光考虑最小化cut(A1,A2,…Ak)，它还同时考虑最大化每个子图点的个数

4.2Ncut

Ncut切法实际上与Ratiocut相似，但Ncut把Ratiocut的分母换成 ，这种改变与之而来的，是L的normalized，这种特殊称谓会在下文说明，而且这种normalized，使得Ncut对于spectral clustering来说，其实更好。

5、总结流程

最常用的相似矩阵的生成方式是基于高斯核距离的全连接方式，最常用的切图方式是Ncut。而到最后常用的聚类方法为K-Means。下面以Ncut总结谱聚类算法流程。

输入：样本集D=(x1,x2,…,xn)，相似矩阵的生成方式, 降维后的维度k1, 聚类方法，聚类后的维度k2
输出： 簇划分C(c1,c2,…ck2)

1) 根据输入的相似矩阵的生成方式构建样本的相似矩阵S

2）根据相似矩阵S构建邻接矩阵W，构建度矩阵D

3）计算出拉普拉斯矩阵L

4）构建标准化后的拉普拉斯矩阵

5）计算最小的k1个特征值所各自对应的特征向量f

6) 将各自对应的特征向量f组成的矩阵按行标准化，最终组成n×k1维的特征矩阵F

7）对F中的每一行作为一个k1维的样本，共n个样本，用输入的聚类方法进行聚类，聚类维数为k2。

8）得到簇划分C(c1,c2,…ck2)

谱聚类算法的优缺点：

谱聚类算法的主要优点是：

1）谱聚类只需要数据之间的相似度矩阵，因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到

2）由于使用了降维，因此在处理高维数据聚类时的复杂度比传统聚类算法好。

谱聚类算法的主要缺点是：

1）如果最终聚类的维度非常高，则由于降维的幅度不够，谱聚类的运行速度和最后的聚类效果均不好。

2) 聚类效果依赖于相似矩阵，不同的相似矩阵得到的最终聚类效果可能很不同。
.