机器人纯跟踪算法 Base Pure Pursuit
前言
纯跟踪算法是一种路径跟踪算法,他通过改变角速度指令将机器人当前位置移动到前面的某个路径点,并不断的跟随路径前进。适用于很多机器人运动学模型,包括阿克曼和全向轮。
本文简单分析求解运动学之后的纯跟踪算法。
原理介绍

如果把机器人当做驴,上图形象的解释了纯跟踪算法的原理,纯跟踪算法需要一直更新“胡萝卜”的位置,让机器人朝着路径的方向前进。
算法
纯跟踪算法的步骤是
- 定位当前机器人的位置。
- 找到路径中匹配的目标点。
- 改变机器人移动的角度。
如何找到匹配点
为了解决这个问题,我们需要先定义路径,我们是在什么样的路径里找到匹配点?
路径
描述一个路径一般是用一些离散的点,如:`(x,y) 。一般而言机器人的移动轨迹是连续的,我们也应该使在路径中找到的匹配点连续, 在算法里我们将这些离散的路径点相连接,变成连续的路径。
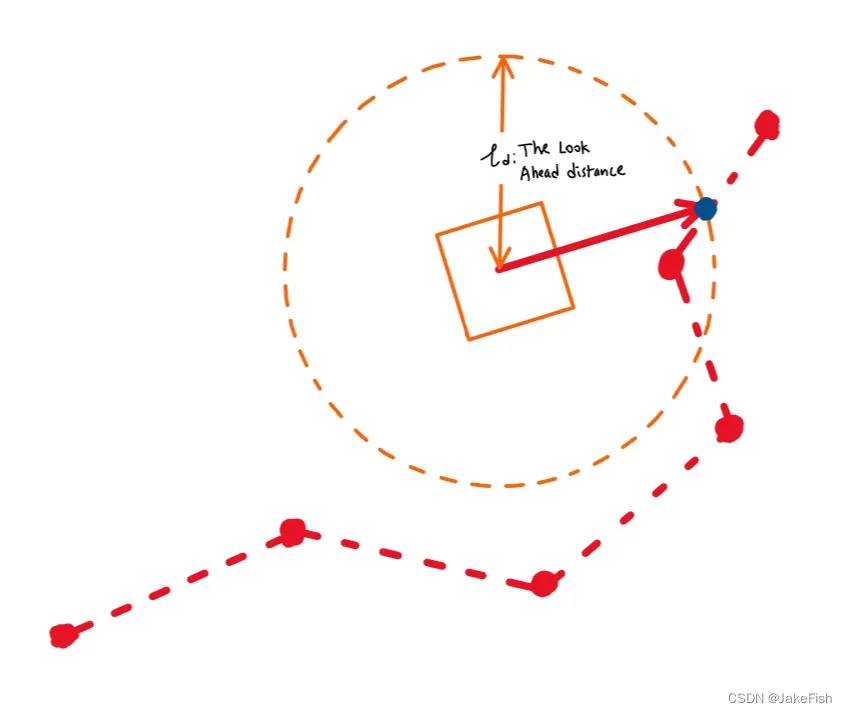
前瞻距离
和上图中人拿着杆子吸引机器人前进一样,我们的算法中也需要一个一定长度的杆子,在此我们定义“杆子”为前瞻距离。
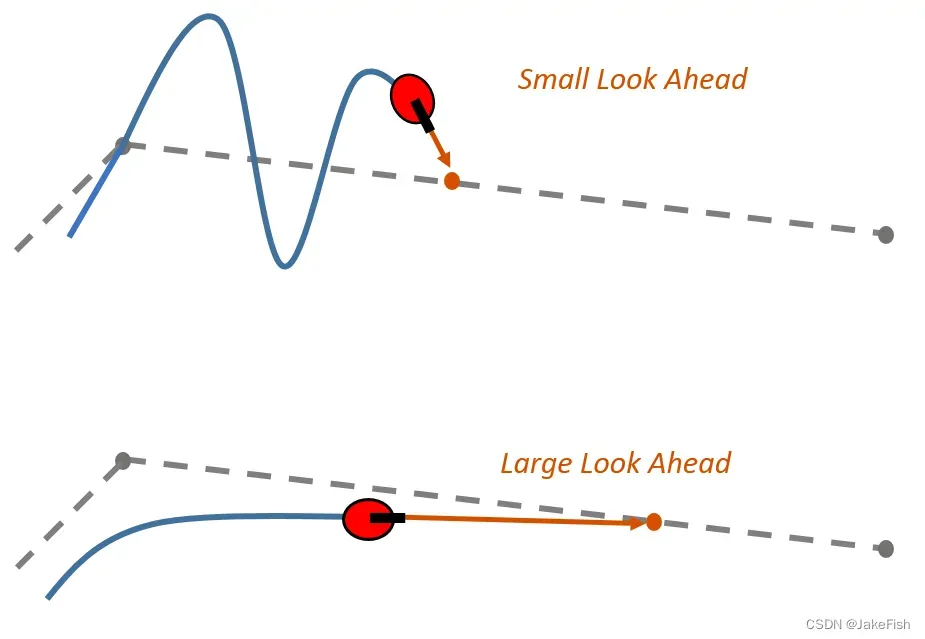
前瞻距离的选取应该与机器人移动的速度相关,太大或太小都不行。如下图就是太长和太短的效果。
匹配点
当我们定义完路径和前瞻距离,接下来就应该解决匹配点。这个问题本质就是直线与圆的交点。
具体而言为路径中连续的两点连接成一直线,而前瞻距离绕机器人当前位置一圈为圆。求这两几何的交点。
圆与直线交点求解
这里可以用公式法或者向量法求解交点,公式法可能会遇到斜率为0的情况,需要分类讨论,在这里我介绍向量法,只需要考虑一种情况。
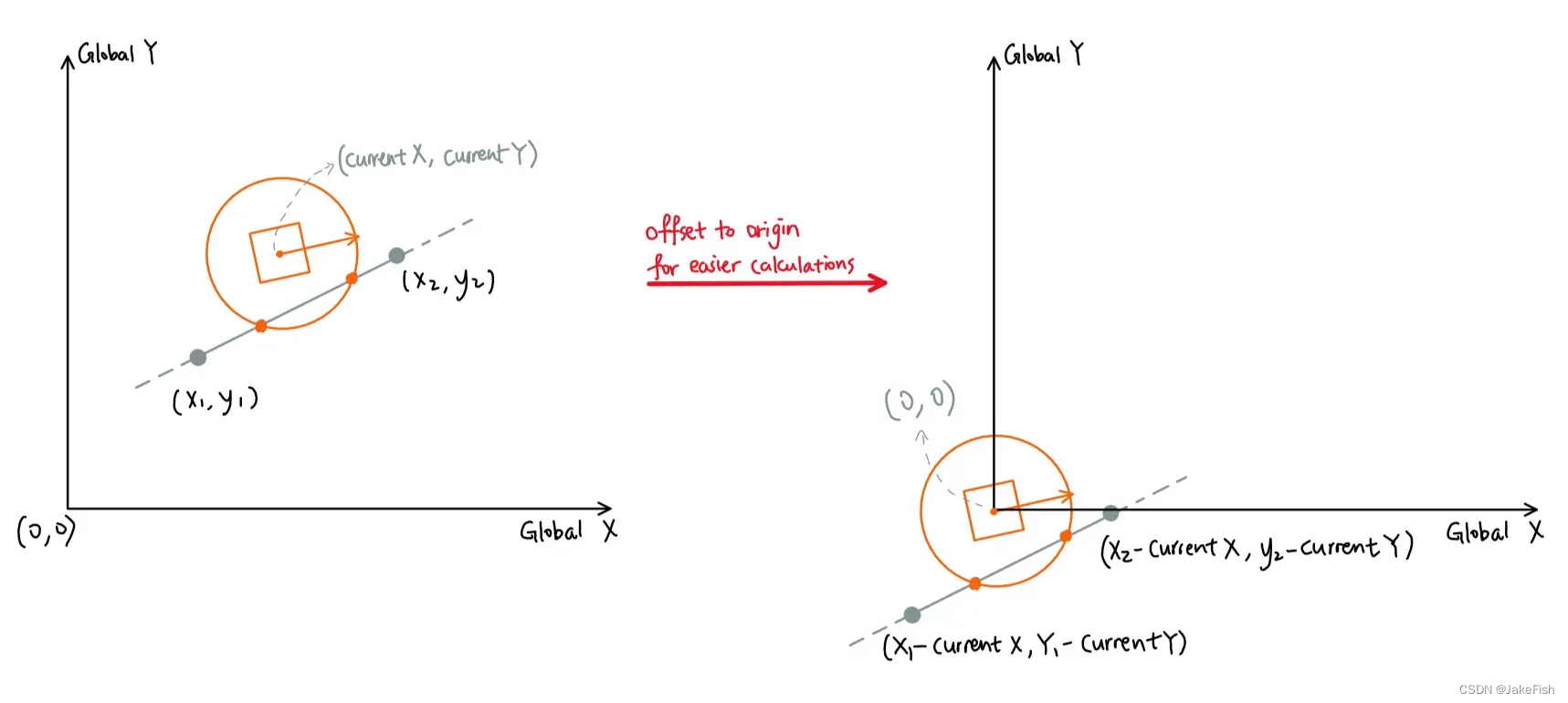
已知,路径点分别为(x1,y1),(x2,y2) 当前机器人位置为(currentX,currentY),前瞻距离为l。
为了简化计算,我们将当前所有的路径点减去机器人的坐标,算出来的交点再加回来即可。
则路径两点变为(x1-currentX,y1-currentY)和(x2-currentXmy2-currentY)
圆的方程为:
直线的方程为: (化为一般式不用考虑斜率为0的情况)
直线到点的距离公式为:
![]()
只取路径间的解
-
情况一:无交点
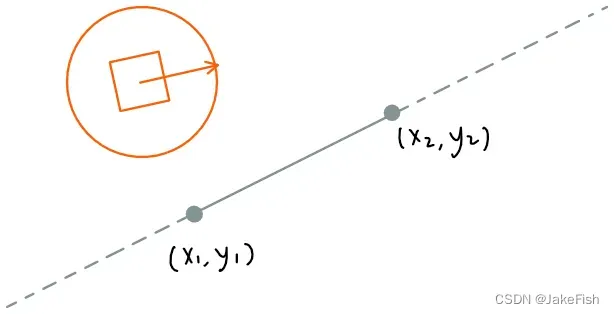
-
情况二:无交点
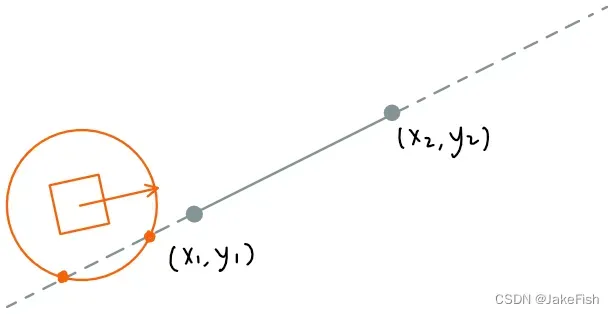
-
情况三:一交点
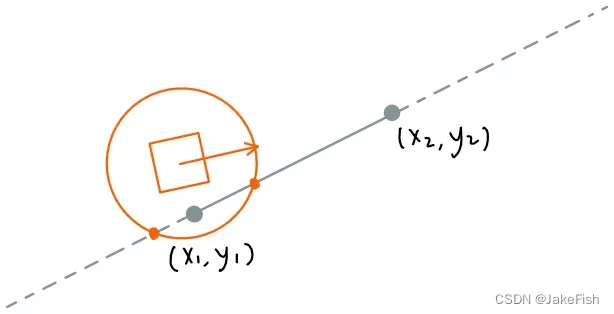
-
情况四:两交点
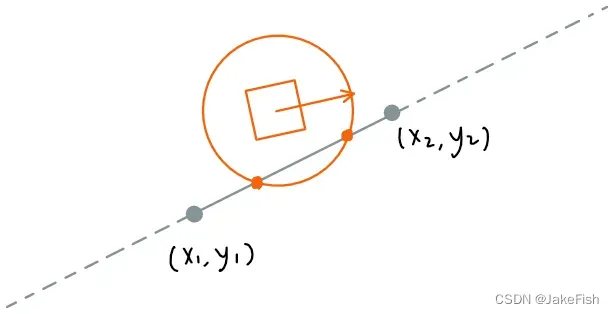
匹配点的判断
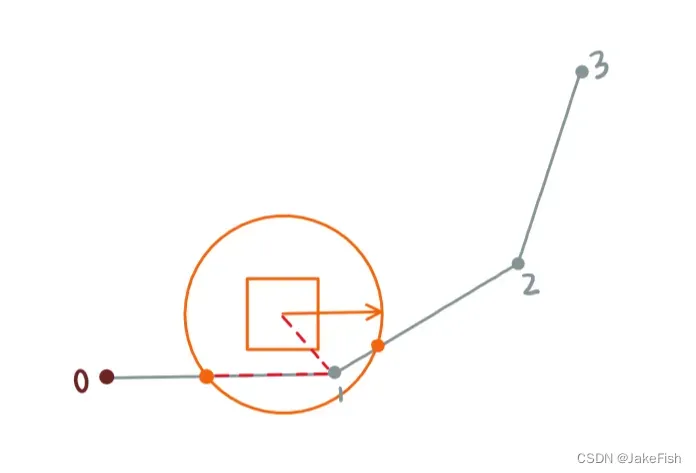
机器人控制
不同的机器人运动学在这一步可能会有所不同,我在此举的是舵轮,需要输入速度方向和底盘角度,在此我输入的是速度方向和底盘角度
,大小为定值1。
效果:
黄色为前瞻距离,红色小球为匹配点
舵轮纯跟踪 ROS2 Control Gazebo 仿真
引用
[1]: base pure pursuit
[2]: mathworks pure puresuit controller
[3]: autoware
[4]: pure pursuit papaer
文章出处登录后可见!
