🌸🌸从今天开始将持续更新数据结构的相关知识点~
🌸首先,从复杂度开始~

复杂度(complexity)
什么是复杂度呢?
从字面来看就是说复杂的程度,我们需要具备一种工具可以评估某种算法(程序)的好坏,比如运行时间、占用空间等等。
复杂度具体体现在三个方面:
1.算法
2.数据规模
3.输入数据的情况(最好情况、最坏情况和平均情况,主要考虑最坏情况)
如何考察程序(算法)的运行时间?
❌直观想法:直接测量时,由于外界环境干扰(比如计算机自身的性能或者其他程序也在运行),因此不能直接完成。
⭕基本假设:理想中的计算机在执行一些步骤时,所用时间是一定的。例如,a=a+1;//是一个加法操作以及一个赋值操作 a=a+b+c;//两个加法操作和一个赋值操作
当执行的步骤越多,程序运行的时间也就越长。
将估算时长的问题转化成了计算程序中基本指令个数的问题。
基本指令:+、-、*、%、&&、||、!、赋值等等。
非基本指令:int a=add( ); int a=5^2;
时间复杂度(time complexity)
public class TestCsdn {
void func(int n) {
int count = 0; //1条基本指令
for(int i = 0; i<2*n;i++) {
count++; //2N条基本指令
}
int M = 10; //1条基本指令
while((M--)>0) {
count++; //10条基本指令
}
System.out.println(count);
}
}执行指令个数:f(N)=(2+C1)N+10+2+C2,即f(N)=aN+b。
当N趋于正无穷时,函数变化关系的比较:
f(n)=a*n+b;
g(n)=c*n^2+b;
对于上面两个函数关系, 当n趋于无穷时f(n)执行的指令个数小于g(n)的指令个数,即f(n)用时较少,所以算法更少。
大O渐进表示法:O(f(n))=O(n) O(g(n))=O(n^2)
大O渐进表示法:
1.只保留最高次项(对最终结果影响的更大的一项);
2.系数变为1(不关心具体的系数)。
时间复杂度的大O渐进表示法:
1.将求运行时间的问题转化成求基本指令个数的问题;
2.求出算法执行指令个数(因变量)和数据规模(自变量)的问题;
3.进而考察在数据规模(n)趋于无穷大时的大小关系;
具体实现:求最坏情况,找到运行次数最多的那条语句,找出n的函数关系,用大O渐进表示法表示,保留最高项将系数化为1。

接下来我们通过几个例题来练习一下:
例题1

函数关系:f(m,n)=a*m+b*n+c
大O渐进表示法:O(m+n)
例题2(循环)

函数关系:f(n)=100(指令个数与n无关,执行了常数次,即n的0次方为最高次,系数化为1)
大O渐进表示法:O(1)
例题3(冒泡排序)
void bubbleSort(int[] array){
for (int end = array.length; end >0 ; end--) {
boolean sorted=true;
for (int i = 1; i <end ; i++) {
if(array[i-1]>array[i]){
Swap(array,i-1,i);
sorted=false;
}
}
if(sorted==true){
break;
}
}

综上我们可以得到一个基本规律,当两层循环嵌套时时间复杂度一般为O(n^2),如下:
for(int i=0;i<n;i++){//循环条件为i=i+2同样适用(加常数)
for(int j=0;j<n;j++){
//基本语句
}
}
///时间复杂度O(n^2)但是,需要特别注意的是,当循环条件为i=i*2(或者其他增长特变快的关系式时),时间复杂度并不是![]() .
.
for(int i=0;i<n;i=i*2){//循环条件为i=i+2同样适用(加常数)
for(int j=0;j<n;j++){
//基本语句
}
}
///时间复杂度O(log(n))例题4(二分查找)


例题5(求阶乘)

时间复杂度:O(n)
例题6(求斐波那契数列)
int fibonacc(int n){
return n<2?n:fibonacc(n-1)+fibonacc(n-2);
//f(n)=f(n-1)+f(n-2)
}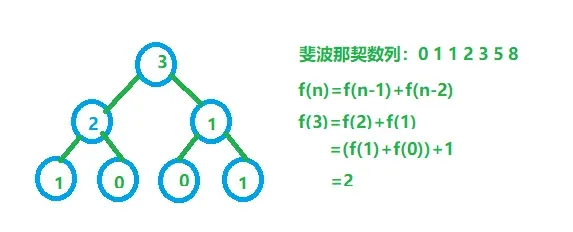
为了方便计算,我们进行估算,即将斐波那契数列近似为等比数列,n为组成的三角形的高度,S(n)为圆形的个数,根据等比数列求和公式:,a1=1,q=2,可得:
即时间复杂度:![]()
常见的时间复杂度
![]() 常数
常数
![]() 线性函数
线性函数
![]() 对数函数
对数函数
![]() 幂函数
幂函数
![]()
![]() 指数函数
指数函数
时间复杂度的具体应用
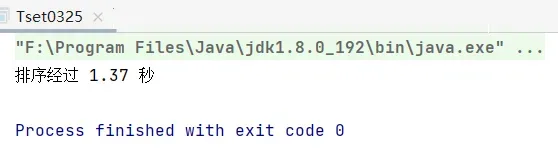
冒泡排序:排序5万个数需要1.37s,冒泡排序的时间复杂度为![]() ,现在排序10万个数,数据规模扩大两倍,即时间复杂度为
,现在排序10万个数,数据规模扩大两倍,即时间复杂度为![]() =
=![]() ,耗时为原来的4被左右。
,耗时为原来的4被左右。
public class Tset0325 {
public static void sort(long[] array){
for (int i = 0; i < array.length-1; i++) {
for (int j = 0; j < array.length-i-1; j++) {
if(array[i]>array[i+1]){
long t=array[i];
array[i]=array[i+1];
array[i+1]=t;
}
}
}
}
public static void main(String[] args){
long[] array=new long[5_0000];
Random random=new Random(); //alt+enter调用Random包
for (int i = 0; i < array.length; i++) {
array[i]=random.nextLong();//向数组中放入随机数
}
//时间戳(毫秒):从某个时刻开始到现在 经过的毫秒数
long s=System.currentTimeMillis(); //获取当前的时间戳(timestamp)以毫秒为单位
sort(array);
long e=System.currentTimeMillis();
long ms=e-s;
double sec=ms/1000.0; //long类型向double类型提升
System.out.printf("排序经过 %.2f 秒\n",sec); //保留小数点后两位
}
}
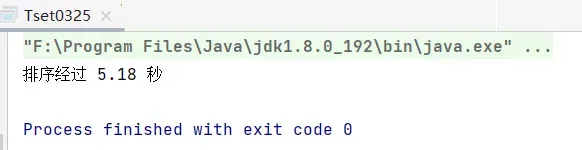
得出结论:数据规模扩大2倍,所用时间扩大4倍。
时间复杂度小结
1.时间复杂度的作用:估算算法的好坏;
2.计算时间复杂度;
3.常见的时间复杂度以及大小关系。
空间复杂度(space complexity)
算法和数据规模的规模之间的函数关系,执行一个算法额外需要多少内存空间。
下面我们通过几个例题来具体看一下如何计算空间复杂度:

例题1(冒泡排序)
void bubbleSort(int[] array){//数组占用的空间是固定的,所以不算在内
//所有的变量本质上都是内存空间的抽象,即每定义一个变量都要在内存上开辟一块空间
for (int end = array.length; end >0 ; end--) {
boolean sorted=true;
for (int i = 1; i <end ; i++) {
if(array[i-1]>array[i]){
Swap(array,i-1,i);
sorted=false;
}
}
if(sorted==true){
break;
}
}空间占用只有3个变量(end、sorted、i),数据规模无论怎么变换,占据的空间是一定长度的,即空间复杂度为O(1)。
例题2(斐波那契数列)
long[] fibonacc(int n){//数据规模是n
long[] fibArray = new long[n+1];
//定义数组时占用空间,引用数据类型(数组对象)放在堆上
fibArray[0]=0;
fibArray[1]=1;
for (int i = 0; i <= n; i++) {
//局部变量放在栈上
fibArray[i]=fibArray[i-1]+fibArray[i-2];
}
return fibArray;
}变量占用的空间是固定的O(1),定义数组时占用空间和数据规模n呈线性关系,因此空间复杂度为O(n)。
栈上占用的空间基本是固定的:O(1)。
堆上占用的空间随着数据规模n而变化。
例题3(求阶乘)
long factorial(int n){
if(n<2){
return n;
}else{
long r=factorial(n-1);
return r*n;
}
}递归调用过程中,factorial(5)没有返回之前,就得执行factorial(4),所以空间是不能释放的,执行factorial(5)时,需要5个空间,和数据规模n呈线性关系,因此空间复杂度是O(n)。
🌸关于复杂度,我们就先认识到这里~

文章出处登录后可见!
