目录
一、什么是RSA算法
在计算机中常用的加密算法分为两类:对称加密算法和非对称加密算法。
1.对称加密
在对称加密技术中,对信息的加密和解密都使用了相同的密钥Key,也就是说使用同一个密钥Key对数据进行加密和解密。这种加密方法可简化加解密的处理过程,信息交换双方都不必彼此研究和交换专用的加解米算法。如果在交换阶段,密钥Key没有泄露,那么加密数据的机密性和报文的完整性就可以得到保证。
2.非对称加密
在非对称加密中,不再只有一个密钥Key了。在非对称加密算法中,密钥被分解为一对,一个称为公开密钥,另一个称为私有密钥。对于公钥,可以通过非保密方式向他人公开,而私钥则由解密方保密,不对别人公开。
3.非对称加密的应用
由于非对称加密方式可以使通信双方无需事先交换密钥就可以建立安全通信,因此被广泛应用于身份认证、数字签名、等信息交换领域。其中最具有代表性的非对称加密方式就是RSA公钥密码体制。
二、RSA算法的基础操作步骤
1.生成公钥和私钥
生成公钥PK和私钥SK的步骤如下:
(1)随意选择两个大的素数P、Q,P不等于Q。
此处在算法实现中需要快速的判断P、Q是否为素数,代码如下:
ll primeNum(ll num) //判断素数
{
if (num == 1 || num == 0)
{
return 0;
}
for (int i = 2; i * i <= num; i++)
{
if (num % i == 0)
{
// 不是素数返回0
return 0;
}
}
return 1; //是素数返回1
}(2)将P、Q两个素数相乘得到一个N,即N=PQ
(3)将P、Q分别减一,再相乘,得到一个数T,即T=(Q-1)*(P-1)
(4)选择一个整数E,作为一个密钥,使E与T互质(即E与T的最大公约数为1),且E必须小于T
此处在算法实现中需要对E与T进行互质的判断(最大公约数为1)
//判断两个数是否互素
ll coprime(ll a, ll b) //判断互质
{
ll t;
if (a < b)
{
t = a;
a = b;
b = t;
}
while (a % b)
{
t = b;
b = a % b;
a = t;
}
//返回值为1,则a,b互素
return b;
}(5)根据公式DE mod T = 1 ,计算出D的值,作为另一个密钥。
此时根据算法,逆向求D
d = 1;
//求e的乘法逆
while (((e * d) % t) != 1)
d++;(6)通过以上的步骤就可以求出N,E,D这三个数据,其中(N,E)作为公钥,(N,D)作为私钥。
(7)生成公钥和私钥后,就可以对外发布了,其中RSA算法的详细的流程图如下:
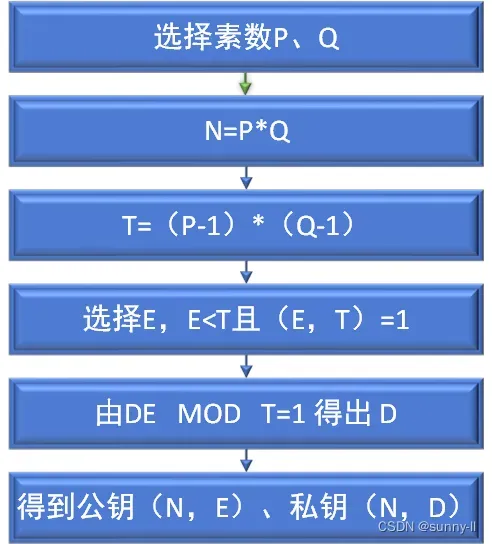
2.用公钥加密信息
发送信息的一方收到公钥PK后,就可以通过公钥PK对数据进行加密,加密的操作步骤如下图所示,其中明文为:M,密文为:C
明文:M
加密:![]()
密文 :C
其中加密的算法,先进行密文的取余运算在加密,代码如下:
//计算密文
ll candp(ll b, ll p, ll k) //b--明文或密文 p--指数(e/d) k--模数
{
if (p == 1)
{
return b % k;
}
if (p == 2)
{
return b * b % k;
}
if (p % 2 == 0)
{
ll sum = candp(b, p / 2, k);
return sum * sum % k;
}
if (p % 2 == 1)
{
ll sun = candp(b, p / 2, k);
return sun * sun * b % k;
}
}在进行加密运算
ll encryption()
{
ll n, e, x, y;
cout << "请输入公钥(e,n)" << endl;
cin >> e >> n;
cout << "请输入明文: (明文需小于" << n << ")" << endl; //计算密文
cin >> x;
y = candp(x, e, n);
cout << "密文为:" << y << endl;
return 0;
}3.用私钥解密信息
接收方持有私钥(N,D)在接受到密文C后,既可以通过私钥解密,得到明文M,解密过程如下:
密文:C
解密:![]()
明文:M
其中解密算法,先产生密钥Key算法:
ll key()
{
ll p, q, t, n, e, d;
cout << "请输入两个素数 p,q: " << endl; //输入两个素数q,p
cin >> p >> q;
if (primeNum(p)==0||primeNum(q)==0)
{
cout << "输入的p或q不是素数" << endl;
return 0;
}
n = p * q;
//t为n的欧拉函数
t = (p - 1) * (q - 1);
cout << "请输入密钥e: " << endl;
cin >> e;
d = 1;
//求e的乘法逆
while (((e * d) % t) != 1)
d++;
cout << "n = p * q = " << n << endl;
cout << "t = (p - 1) * (q - 1) = " << t << endl;
cout << ("公钥(e,n)为:(") << e << "," << n << ")" << endl;
cout << ("私钥(d,n)为:(") << d << "," << n << ")" << endl;
return 0;
}在进行解密:
ll decode()
{
ll n, d, x, y;
cout << "请输入私钥(d,n)" << endl;
cin >> d >> n;
cout << "请输入密文: "; //计算密文
cin >> y;
x = candp(y, d, n);
cout << "明文为:" << x << endl;
return 0;
}三、AC代码
新建一个头文件RSA.h
#pragma once
#include <stdio.h>
#include <iostream>
#include <stdlib.h>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
// 判断素数
ll primeNum(ll num);
// 判断互质
ll coprime(ll a, ll b);
// 计算密文
ll candp(ll b, ll p, ll k);
// 生成密钥
ll key();
//加密
ll encryption();
//解密
ll decode();
// 菜单
void menu();将函数写在RSA.cpp中,用于主函数RSA()的调用代码如下:
#define _CRT_SECURE_NO_WARNINGS 1
#include "RSA.h"
void menu()
{
printf("------------------------------------------\n");
printf("***** 请选择所需功能 *****\n");
printf("***** 1.生成钥匙 *****\n");
printf("***** 2.加密 *****\n");
printf("***** 3.解密 *****\n");
printf("***** 4.退出 *****\n");
printf("------------------------------------------\n");
}
ll primeNum(ll num) //判断素数
{
if (num == 1 || num == 0)
{
return 0;
}
for (int i = 2; i * i <= num; i++)
{
if (num % i == 0)
{
// 不是素数返回0
return 0;
}
}
return 1; //是素数返回1
}
//判断两个数是否互素
ll coprime(ll a, ll b) //判断互质
{
ll t;
if (a < b)
{
t = a;
a = b;
b = t;
}
while (a % b)
{
t = b;
b = a % b;
a = t;
}
//返回值为1,则a,b互素
return b;
}
//计算密文
ll candp(ll b, ll p, ll k) //b--明文或密文 p--指数(e/d) k--模数
{
if (p == 1)
{
return b % k;
}
if (p == 2)
{
return b * b % k;
}
if (p % 2 == 0)
{
ll sum = candp(b, p / 2, k);
return sum * sum % k;
}
if (p % 2 == 1)
{
ll sun = candp(b, p / 2, k);
return sun * sun * b % k;
}
}
//生成密钥
ll key()
{
ll p, q, t, n, e, d;
cout << "请输入两个素数 p,q: " << endl; //输入两个素数q,p
cin >> p >> q;
if (primeNum(p)==0||primeNum(q)==0)
{
cout << "输入的p或q不是素数" << endl;
return 0;
}
n = p * q;
//t为n的欧拉函数
t = (p - 1) * (q - 1);
cout << "请输入密钥e: " << endl;
cin >> e;
d = 1;
//求e的乘法逆
while (((e * d) % t) != 1)
d++;
cout << "n = p * q = " << n << endl;
cout << "t = (p - 1) * (q - 1) = " << t << endl;
cout << ("公钥(e,n)为:(") << e << "," << n << ")" << endl;
cout << ("私钥(d,n)为:(") << d << "," << n << ")" << endl;
return 0;
}
//加密
ll encryption()
{
ll n, e, x, y;
cout << "请输入公钥(e,n)" << endl;
cin >> e >> n;
cout << "请输入明文: (明文需小于" << n << ")" << endl; //计算密文
cin >> x;
y = candp(x, e, n);
cout << "密文为:" << y << endl;
return 0;
}
//解密
ll decode()
{
ll n, d, x, y;
cout << "请输入私钥(d,n)" << endl;
cin >> d >> n;
cout << "请输入密文: "; //计算密文
cin >> y;
x = candp(y, d, n);
cout << "明文为:" << x << endl;
return 0;
}在写出主函数test.c,对上面的函数进行调用即可:
#include "RSA.h"
void RSA()
{
while (1)
{
menu();
ll i = 0;
cin >> i;
switch (i)
{
case 1:
key();
break;
case 2:
encryption();
break;
case 3:
decode();
break;
case 4:
exit(0);
default:
cout << "输入错误,请重新输入" << endl;
}
}
}
void menu1()
{
printf("******************************************\n");
printf("******************************************\n");
printf("***** 欢迎来到RSA加密测试系统 ******\n");
printf("******************************************\n");
printf("******************************************\n");
}
int main()
{
menu1();
RSA();
return 0;
}六、RSA算法的测试
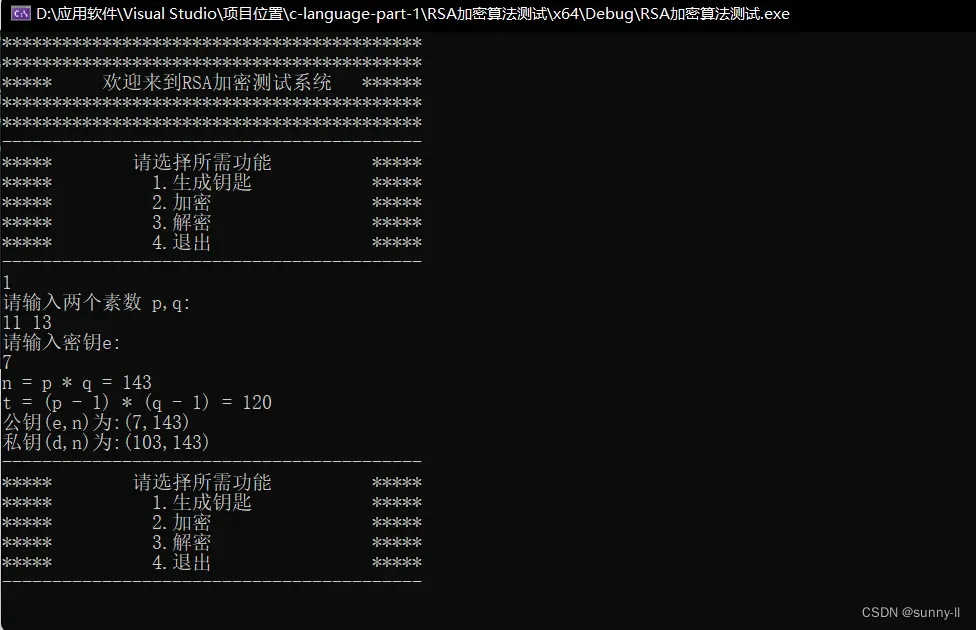
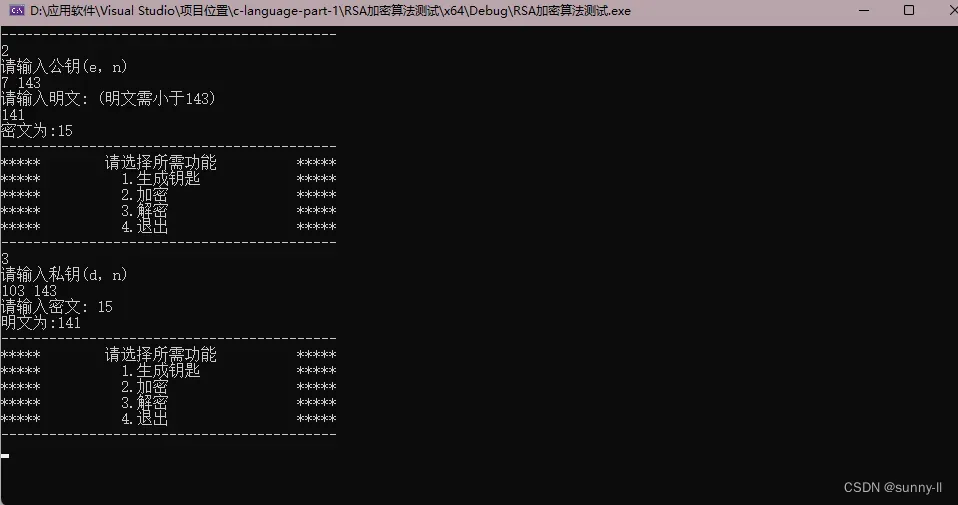
七、共勉
以下就是我对RSA算法的理解,如果有不懂或者有问题的小伙伴可以在评论区里说出来哦,我们一起加油哦!!!
版权声明:本文为博主作者:sunny-ll原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/weixin_45031801/article/details/126728082
