向量点积公式推导（绝对尽量不含糊~~）

一。向量点积公式

先给个向量内积的定义，也叫向量点积

同时它还满足如下公式。

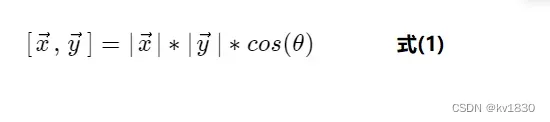
有了上面两个公式呢，就可以很方便地求出两个向量的夹角了，下面的定义3，其实就是根据上面的式(1)转换得到

比如x=(1,0)，y=(1, 1)，

由定义1，[x, y]=1*1+0*1=1

∣x∣∗∣y∣=1∗ $\sqrt{2}$

那么cos( $\theta$ )=[x, y]/(∣x∣∗∣y∣)=1/ $\sqrt{2}$

$\theta$ 就是45度啦

可以看出求夹角非常地方便。式1中的公式它为什么能成立呢，把它细化一下，就是下式为什么能成立呢？

x1x2+y1y2+…+xnyn=∣x∣∗∣y∣∗ cos( $\theta$ ) —————–式(2)

二。分析

先说明一点，我们最终要证的就是式（2）:x1x2+y1y2+…+xnyn=∣x∣∗∣y∣∗cos( $\theta$ )

1.式2右半边的理解

式(2)的右边的含义很明确，向量的内积就是向量y在向量x上的投影长度(即 ∣y∣*cos( $\theta$ ) )与x的模相乘，

当然反过来也是一样，也可以说是向量x在向量y上的投影长度 (即 ∣x∣*cos( $\theta$ ) )与y的模相乘，就看你想把cos ( $\theta$ )跟谁结合了。

注意，这才是向量点积的真正含义！

2.式2左边半

没啥好说的，定义1已经说了，咱定义了它就是向量的内积。但是如果我们又定义了式（2）的右边也是向量内积，所以说左边等于右边，那这肯定是扯淡~~。

同理，如果有人说定义不用证明，那也是在扯淡。

问题是左边真的等于右边吗？下面先给出二维平面上的证明。

三。二维平面上的证明

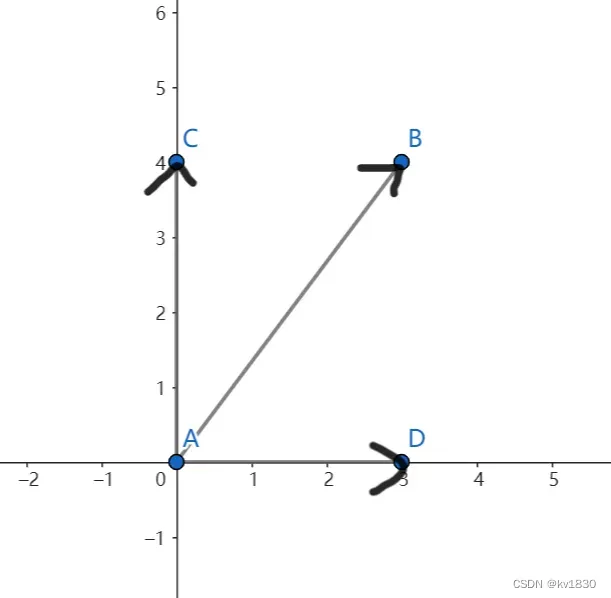
1.复习一下向量加法

先复习一下，一个向量可以分解为延着x坐标和延着y坐标的两个分向量的和，如上图，因为 $\vec{AB}=\vec{AC}+\vec{CB}=\vec{AC}+\vec{AD}$

为了避免混淆，把式(2)先改一下，改为a向量和b向量，并且改为2维平面的情况

$a_{x} b_{x} +a_{y} b_{y }$ =∣a∣∗∣b∣∗cos( $\theta$ ) ——–式(3)

注：式（3）的ax的意思是向量a的x分量值，是一个值，不是向量（它上面没有箭头，也没有加粗，下面注意区别）

2.证明

接下来，我们先从式（3）左边入手，还是右边入手呢？都不。。。我们得从向量点积的真正含义入手，上面分析过了，见二(1)。现在为了方便书写，就用一个实心点表示向量点积符号，即： $\vec{a} \bullet \vec{b}$ ，并且注意，跟据它的含义，它是等于 ∣a∣∗∣b∣∗cos( $\theta$ )的！，所以我们现在认可的是式3的右边，我们暂不认何左边。

$\vec{a} \bullet \vec{b} =(\vec{a_{x}}+\vec{a_{y}}) \bullet (\vec{b_{x}}+\vec{b_{y}})$ ——式(4)

$\vec{a} \bullet \vec{b} =\vec{a_{x}}\bullet\vec{b_{x}}+\vec{a_{x}}\bullet\vec{b_{y}}+\vec{a_{y}}\bullet\vec{b_{x}}+\vec{a_{y}}\bullet\vec{b_{y}}$ ——式(5) 因为符合分配律

接下来，由于点积的含义

$\vec{a_{x}}\bullet\vec{b_{y}}=|\vec{a_{x}}|*|\vec{b_{y}}|*cos( \theta )=0$ ，因为这里的θ角是延着x轴、y轴的两个向量的夹角，是90度，cos(θ)就是0了

同理 $\vec{a_{y}}\bullet\vec{b_{x}}=|\vec{a_{y}}|*|\vec{b_{x}}|*cos( \theta )=0$

所以:

$\vec{a} \bullet \vec{b} =\vec{a_{x}}\bullet\vec{b_{x}}+\vec{a_{y}}\bullet\vec{b_{y}}=|\vec{a_{x}}|*|\vec{b_{x}}|*cos( \theta_1 )+|\vec{a_{y}}|*|\vec{b_{y}}|*cos( \theta_2 )=a_{x}b_{x}+a_{y}b_{y}$ ，因为θ1、θ2都是0度，cos值就是1啦。

最终，成功证明了：

$\vec{a} \bullet \vec{b} =|\vec{a}|*|\vec{b}|*cos( \theta)=a_{x}b_{x}+a_{y}b_{y}$

3.向量点积符合分配律？

(1)质疑

等等，其实并没有证明结束，上面的证明用了一个性质，是关键的环节，但是我们其实完全不知道它对不对！就是说向量点积符合分配律，从而实现从式4到式5的转变

$\vec{a} \bullet \vec{b} =(\vec{a_{x}}+\vec{a_{y}}) \bullet (\vec{b_{x}}+\vec{b_{y}})$ ——式(4)

$\vec{a} \bullet \vec{b} =\vec{a_{x}}\bullet\vec{b_{x}}+\vec{a_{x}}\bullet\vec{b_{y}}+\vec{a_{y}}\bullet\vec{b_{x}}+\vec{a_{y}}\bullet\vec{b_{y}}$ ——式(5)

我们知道，四则运算是符合分配律的，但是我不准备证明这玩意儿，也不准备质疑它。但是你不能说现在我们随意新定义了一种运算，然后我们就说它符合分配律，那肯定是扯淡！

(2)扯淡环节

如果你不信的话，下面插播一段扯淡环节，我现在定义一个运算符，叫做“绝对乘”，符号我想好了，就是：|*|，就是两个竖杠中间夹了一个乘号（星号），为了好识别我把我发明的符号加个粗标个红色，它的运算方法是，两个数做绝对乘，就是把两个数的绝对值乘起来，接下来我说它符合分配律！来验证一下：

0|*|10=(-1+1)|*|10=-1|*|10+1|*|10=|-1|*|10|+|1|*|10|=20，

但是不对啊，0|*|10=|0|*|10|=0啊，完了，它明显不符合分配律！

(3)证明

如果向量点积真不符合分配律，那不完犊子了，没法证了。所以接下来我们就证明一下（或者说验证一下，实力有限，可能不是完美证明），它倒底符不符合分配律。

我们先简化一下，就证下面这个就行了，因为如果b可以分开来乘了，a自然也可以分开来乘了。

注意，我们这里其实证的并不是向量点积是否符合分配律，因为向量bx和向量by分别是延着x轴、y轴方向的，这是限制条件！并且在2.证明中，我们也是基于这个限制条件的，所以我们只要证明这限制条件下的分配律成立，其实就可以了。

$\vec{a} \bullet \vec{b} =\vec{a}\bullet (\vec{b_{x}}+\vec{b_{y}})=\vec{a}\bullet\vec{b_{x}}+\vec{a}\bullet\vec{b_{y}}$ —-式(6)

接下来，画图证明：

AB就是向量a，AC就是向量b，我们现在要证明的是向量b和向量a的点积等于向量bx和向量a的点积加上向量by和向量a的点积，证明了它，就证明式6成立。

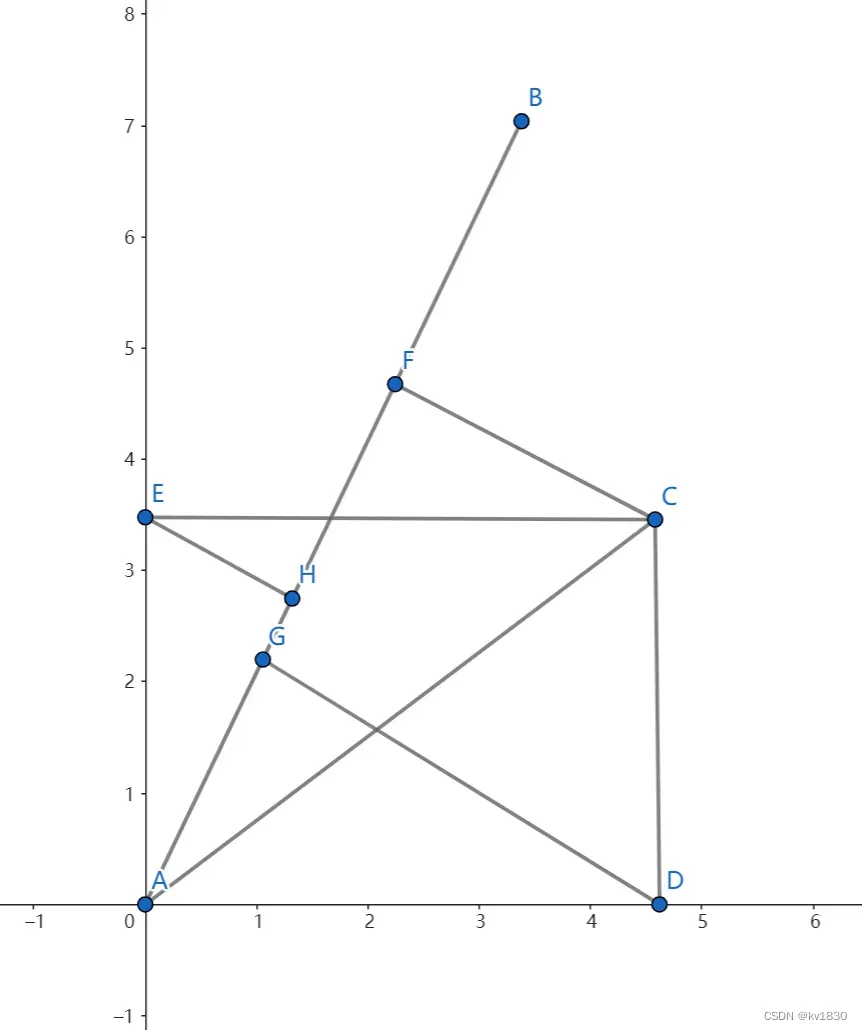
然后仍然是从向量点积的含义入手，我们唯一能确定的东西就是它的含义，因为它是我们新定义一个运算符！（在推导式3的时候，我们就可以这么设想~~）。

向量a和向量b的点积就是向量AC在向量AB上的投影即AF的长度乘上AB的长度。

向量AC的x分量就是向量AD，向量AD与向量AB的点积就是AC在AB上的投影即AG乘上AB

同量，向量AC的y分量就是向量AE，AE与AB的点积就是AH乘AB

即：

$\vec{a} \bullet \vec{b} =AB*AF$

$\vec{a} \bullet \vec{b_x} =AB*AG$

$\vec{a} \bullet \vec{b_y} =AB*AH$

三者都有AB，所以如果我们能证明：AF=AG+AH，那就可以推导出式6了，即：

$\vec{a}\bullet (\vec{b_{x}}+\vec{b_{y}})=\vec{a}\bullet\vec{b_{x}}+\vec{a}\bullet\vec{b_{y}}$

再观察一下上图：

AF=AH+HF

那只要证明AG=HF，就OK了。现在加一点标记，标了3个角，它们的角度相同，都等于向量a和向量b的夹角θ，又标了一个点I（箭头处）：

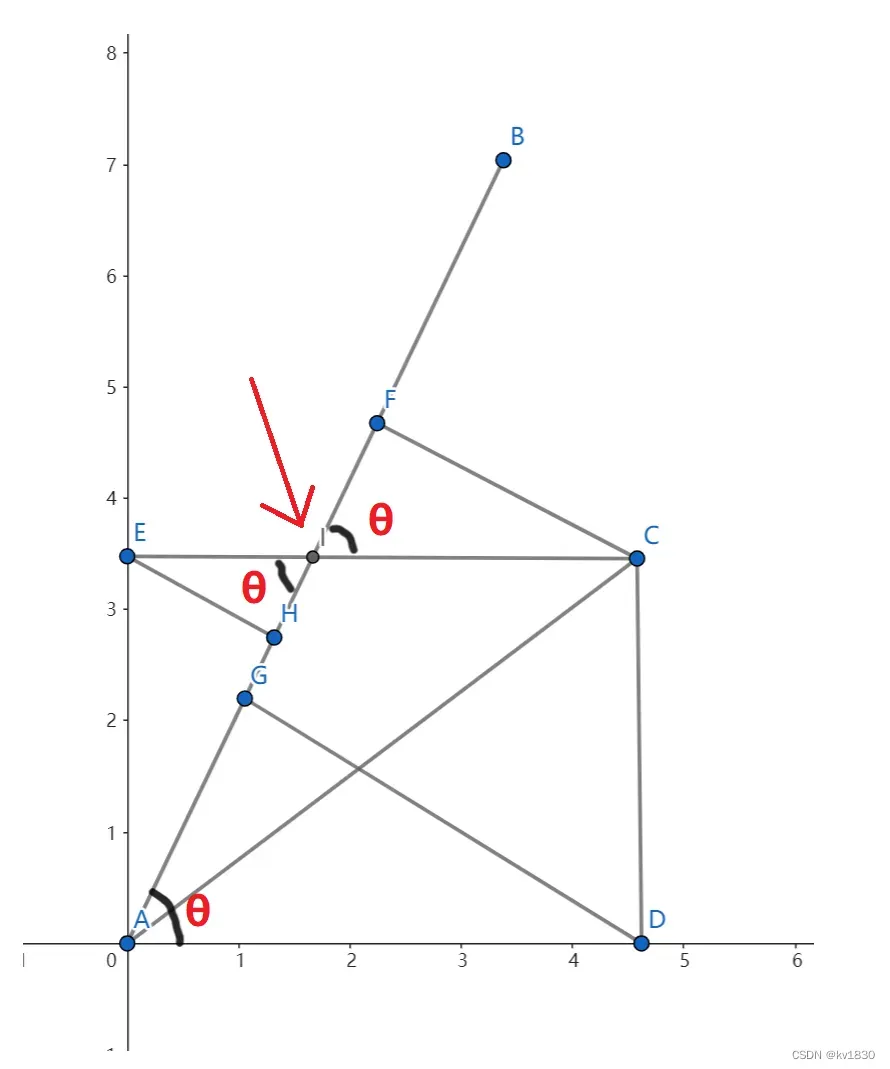
AG=AD*cos(θ)

HF=EI*cos(θ)+IC*cos(θ)=EC*cos(θ)=AD*cos(θ)

完事儿了，AG=HF!

所以最终我们推导出了公式6！即 $\vec{a}\bullet (\vec{b_{x}}+\vec{b_{y}})=\vec{a}\bullet\vec{b_{x}}+\vec{a}\bullet\vec{b_{y}}$

所以向量点积是满足分配律的！2.证明的步骤完全成立！

注：这个图可能随着不同的角度会有一些变化，但是证明的方法都是一样的。

(4)那没限制条件的分配律还能证吗？

虽然说有限制条件的分配律证明了，就可以推导向量点积公式了，但是不禁好奇，没限制条件的呢，比如下式是否成立，向量c和向量d没有限制条件。

$\vec{a}\bullet (\vec{c}+\vec{d})=\vec{a}\bullet\vec{c}+\vec{a}\bullet\vec{d}$ ——式(7)

$\vec{a}\bullet (\vec{c}+\vec{d})=\vec{a}\bullet (\vec{c_{x}}+\vec{c_{y}}+\vec{d_{x}}+\vec{d_{y}})=\vec{a}\bullet (\vec{c_{x}}+\vec{d_{x}})+\vec{a}\bullet (\vec{c_{y}}+\vec{d_{y}})$ —-式(8)，因为向量cx加向量dx是延着x轴方向的，向量cy加向量dy是延着y轴方向的，所以可以分开来乘，(（3）里面已经证过了）

$\vec{a}\bullet (\vec{c_{x}}+\vec{d_{x}})+\vec{a}\bullet (\vec{c_{y}}+\vec{d_{y}})=\vec{a}\bullet \vec{c_{x}}+\vec{a}\bullet \vec{d_{x}}+\vec{a}\bullet \vec{c_{y}}+\vec{a}\bullet \vec{d_{y}}$ —–式(9) 这一步的展开毫无疑问，从向量点积的含义上可以直接证明，单独看一项就是下式。

$\vec{a}\bullet (\vec{c_{x}}+\vec{d_{x}})=\vec{a}\bullet \vec{c_{x}}+\vec{a}\bullet \vec{d_{x}}$

向量cx和dx是同方向的，其向量和的长度就相于两个向量长度的和，然后它们在a上的投影都是乘以同一个cos(θ)，那肯定是相等的了，不详写了。

继续接式(9)，把它重新组合一下，向量cx和向量cy合一起，向量dx和向量dy合一起，得到：

$\vec{a}\bullet \vec{c_{x}}+\vec{a}\bullet \vec{c_{y}}+\vec{a}\bullet \vec{d_{x}}+\vec{a}\bullet \vec{d_{y}}=\vec{a}\bullet (\vec{c_{x}}+\vec{c_{y}})+\vec{a}\bullet (\vec{d_{x}}+\vec{d_{y}})=\vec{a}\bullet \vec{c}+\vec{a}\bullet \vec{d}$ ——-式(10)

证明完毕！

如果这里要问一下，为啥能合起来，即下式为啥成立？

$\vec{a}\bullet \vec{c_{x}}+\vec{a}\bullet \vec{c_{y}}=\vec{a}\bullet (\vec{c_{x}}+\vec{c_{y}})$

这个式子就是之前的式(6)啊，只是把等号左右两边交换了下而已，把式(6)再贴一下给你看看：

$\vec{a} \bullet \vec{b} =\vec{a}\bullet (\vec{b_{x}}+\vec{b_{y}})=\vec{a}\bullet\vec{b_{x}}+\vec{a}\bullet\vec{b_{y}}$ —-式(6)

所以，由式(8),(9),(10)得到，向量点积真的符合分配律！

四。多维空间上还是否成立？

其实2.证明里的步骤完全可以写成多维的形式，比如加一维，写成下面这样，然后还是拆开乘就行了

$\vec{a} \bullet \vec{b} =(\vec{a_{x}}+\vec{a_{y}}+\vec{a_{z}}) \bullet (\vec{b_{x}}+\vec{b_{y}}+\vec{b_{z}})$

关键是多维空间的向量点积是否符合分配律？答案应该（也许可能大概）是符合啊，你看我下面扯的对不对啊。

二维空间我们证过了，符合分配律，所以下式是成立的，向量bx和向量byz是在一个平面上的

$\vec{a}\bullet \vec{b}=\vec{a}\bullet (\vec{b_{x}}+\vec{b_{y}}+\vec{b_{z}})=\vec{a}\bullet (\vec{b_{x}}+\vec{b_{yz}})=\vec{a}\bullet\vec{b_{x}}+\vec{a}\bullet\vec{b_{yz}}$

然后：

$\vec{a}\bullet \vec{b_{yz}}=\vec{a}\bullet (\vec{b_{y}}+\vec{b_{z}})=\vec{a}\bullet\vec{b_{y}}+\vec{a}\bullet\vec{b_{z}}$

所以下式成立：

$\vec{a}\bullet \vec{b}=\vec{a}\bullet (\vec{b_{x}}+\vec{b_{y}}+\vec{b_{z}})=\vec{a}\bullet\vec{b_{x}}+\vec{a}\bullet\vec{b_{y}}+\vec{a}\bullet\vec{b_{z}}$

所以在3维平面也符合分配律！从而3维平面上的点积公式3也成立！

那么可能又问，那n维空间呢？其实完全可以把上面这一段改一下，改为证明：假设n维空间向量点积符合分配律，那么n+1维空间是否还符合。（当然是OK的喽，我就懒得再写一遍了）

然后由于2维空间符合分配律，由数学归纳法得知，任意n维空间都符合分配律。从而再由2.证明改一下得出任意n维空间都符合向量点积公式3

原文链接：https://blog.csdn.net/ogebgvictor/article/details/129103852