1. 模型评估
本章主要讲如何测量一个模型,当模型已经训练好时
1. 模型指标
- 在监督学习中,损失通常用作衡量模型质量的指标。
- 还有其他各种指标:
- 模型相关的指标:分类问题评估精度,目标检测问题评估mAP
- 业务相关指标:营业收入、延迟
- 通常根据多个指标选择模型
1.1 举例广告投放
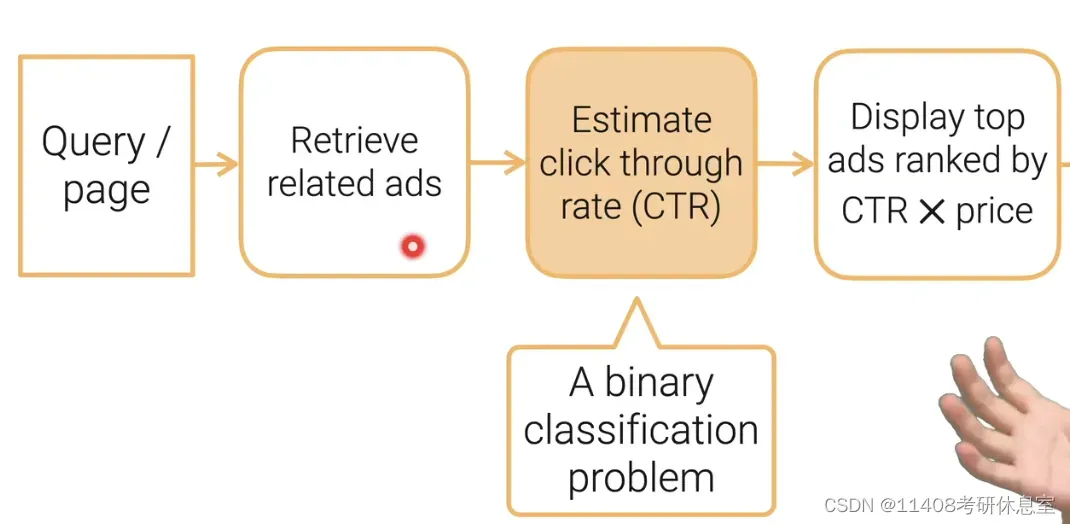
1.2 常见分类问题的指标
1.2.1 准确度Accuracy = 正确预测样本大小/样本大小
- 样本中正确预测的比例
1.2.2 精度Precision = 预测正确为类i的个数/我预测成类i的样本的个数
1.2.3 召回率Recall = 预测正确为类i的样本个数/类i的样本个数
1.2.4 F1:做调和平均 2pr/(p+r)
- 用于平衡精度和召回率
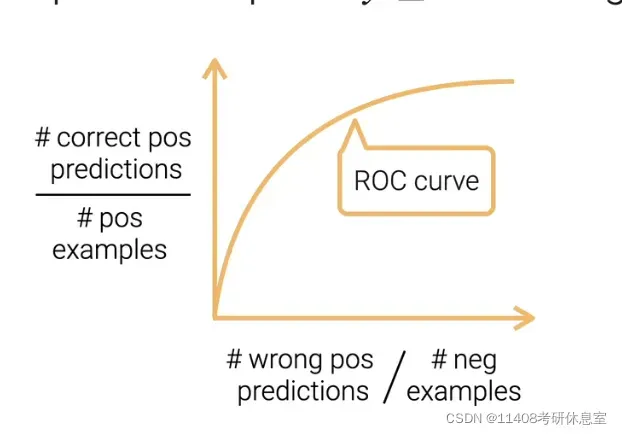
1.3 AUC & ROC
- x轴分子:预测成负例但实际是正的,x轴分母:负例样本个数
- y轴分子:预测成正例实际也是正的,y轴分母:正例样本个数
- 模型每次选择不同的
,如果
被预测为正例,否则为负例
- 不断的选取
作图就是ROC曲线,AUC是曲线ROC下面的面积
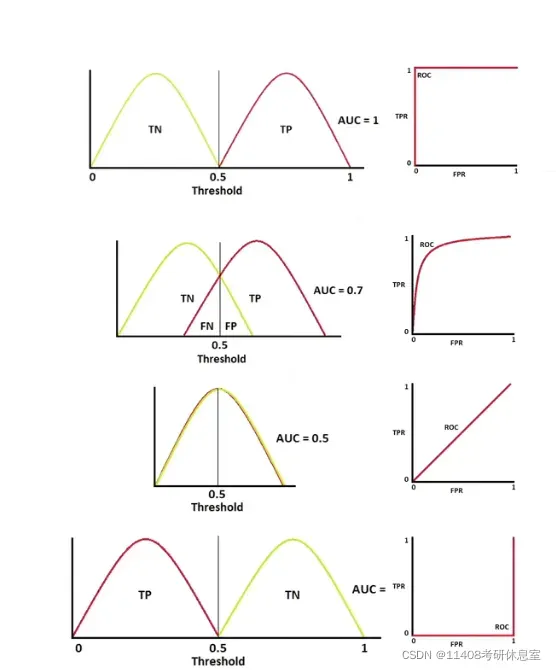
1.3.1 AUC好坏(AUC 0.5是最糟糕,1是最高,我们需要把AUC从0.5优化到1)
- 图1显示正反例可以完全分离
- 图2展示了一些不太容易区分的正反例子
- 图 3 显示正反例是完全整合的,是随机的
- 图 4 显示了正面和负面的例子是相反的。
1.4 商业指标,以广告投放为例(提高收入、增加用户体验)
- 延迟
- 每页显示的平均广告数
- 广告点击率
- 每个广告的点击价格
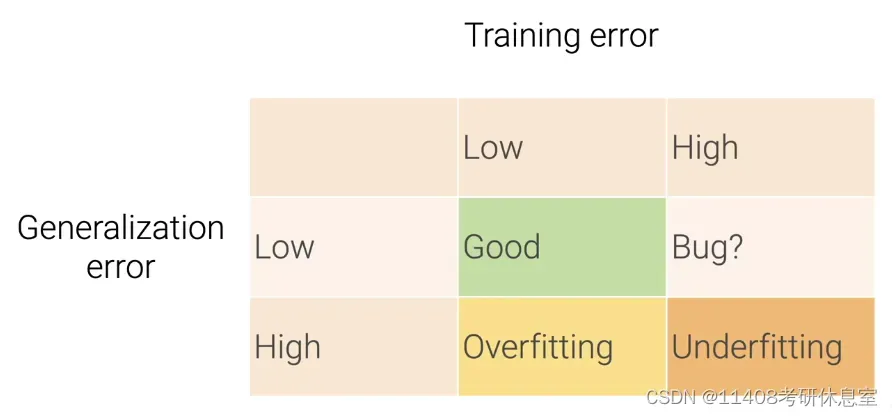
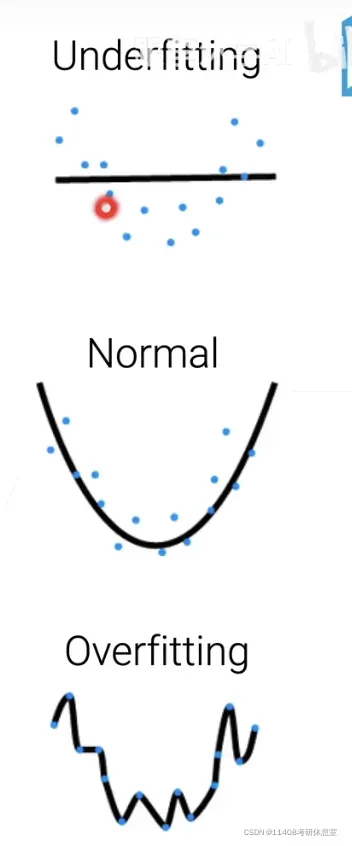
2. 过拟合和欠拟合
- 欠拟合:训练误差和泛化误差都很高
- 过拟合:低训练误差,高泛化误差
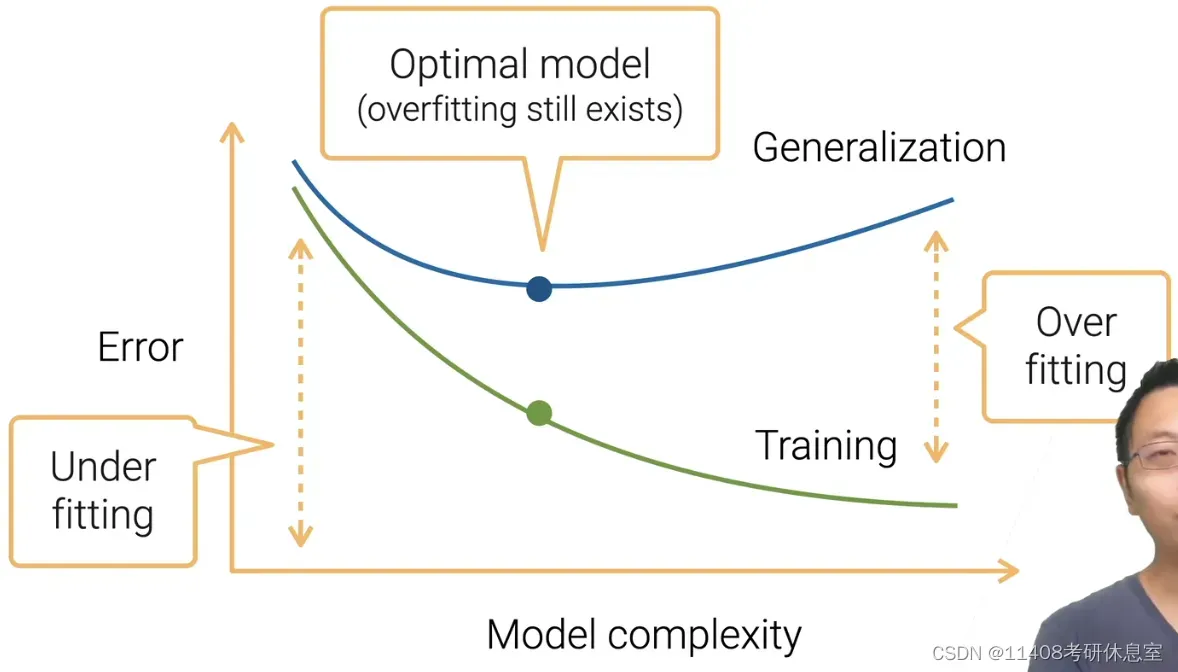
2.1 训练和泛化误差
2.1.1 训练误差:在训练数据上看到的模型误差
2.1.2 泛化误差:在新的数据上的模型误差
- 训练误差低并不意味着泛化误差也会降低(过去的好成绩不代表未来的好成绩)
2.2 数据和模型的复杂度
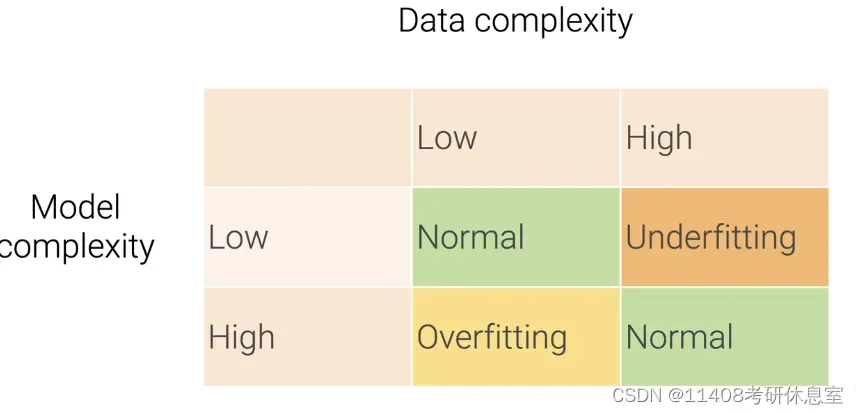
2.2.1 模型复杂度:能够去拟合各种各样的函数的能力
- 比较不同的算法更加困难
- eg:树 vs 神经网络
- 在类似的模型中,可以进行相对比较
- 可学习参数个数,树的层数,隐藏层数
- 参数可以取多少个值,取值有没有限制(正则化)
2.2.2 模型复杂度的影响
2.2.3 数据复杂度:信息量的多少
- 影响因素:样本个数、每个样本的元素、时间/空间结构、样本多样性
- 不同的数据很难进行比较,eg:图片和文本进行比较
2.3 模型复杂度 vs 数据复杂度
- 给定一个简单模型(线性模型),增加数据复杂度,模型会从overfitting->underfitting,当再往后增加数据复杂度,泛化误差不再继续降低了
- 这时,需要更换一个复杂的模型(深度神经网络)。当数据不复杂时,简单模型的泛化误差小于复杂模型的泛化误差。当数据复杂度达到一定程度时,复杂模型的泛化误差逐渐减小。
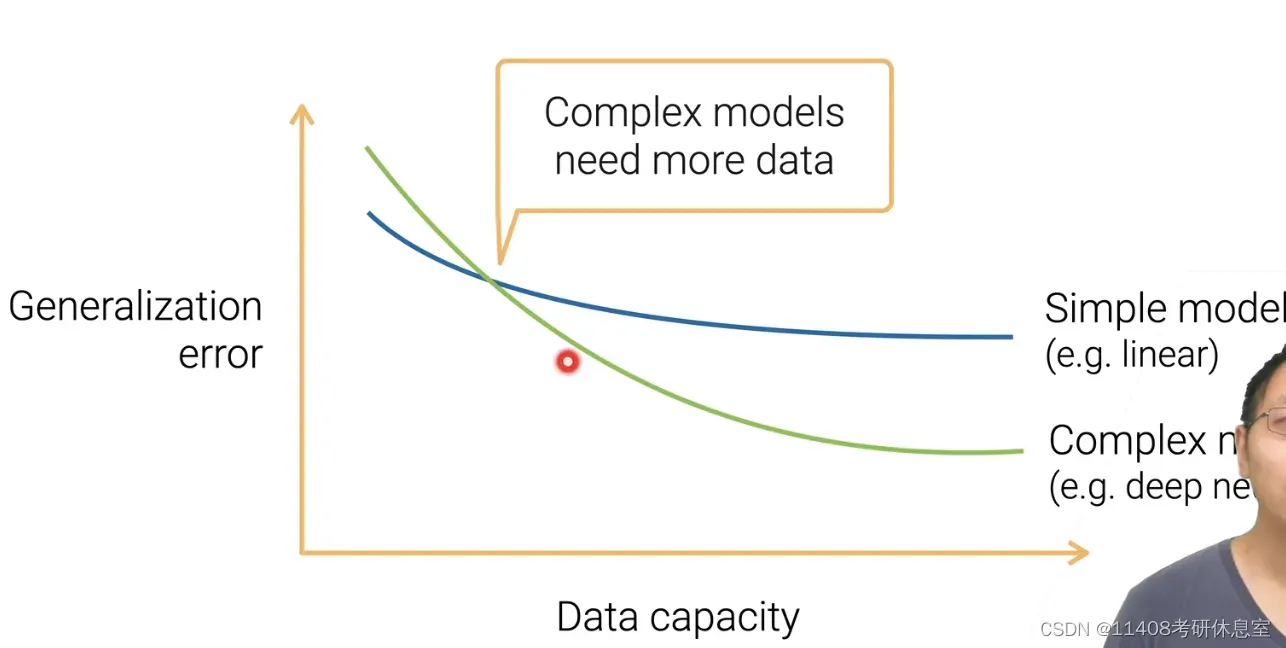
- 结论:在工业界,当数据比较少的时候,先从简单的模型开始。当数据复杂,模型不够好时,换成复杂模型。即所选模型的复杂度应与数据的复杂度相匹配,避免过拟合和欠拟合。
3. 模型验证
3.1 估计泛化误差
- 测试数据集:只能使用一次
- 验证数据集:可多次使用
- 是训练数据集的一部分
- 通常是测试集,实际上是指验证集
3.2 生成验证数据集
3.2.1 把样本数据随机的分成训练和验证集(验证集误差近似作为泛化误差)
3.2.2 随机的选取%n样本作为验证集(n=50,40,30,20,10)
3.2.3 不是独立同分布的数据拆分(训练集和验证集)
- 不能随机拆分数据
- 包含时间序列信息:房屋销售、股票价格
- 验证集需要在训练集之后
- 样本可能属于多个分组:eg,人脸图片
- 此时需要分组而不是随机分组
- 数据不平衡(有的类多,有的类少)
- 具有更多类的样本被更多地采样
3.2.4 K折交叉验证(数据不够多的时候)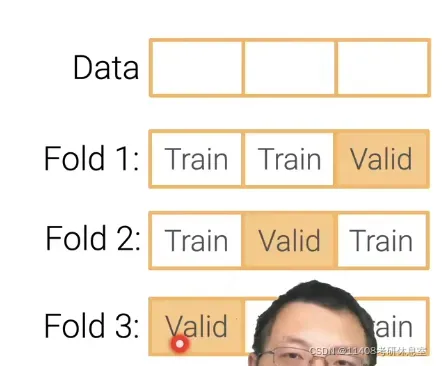
- 算法流程
- 把训练机数据切成K块
- 每一次,把第i个块拿出来作为验证集,剩下的做训练集
- 最后把k个块的平均误差作为结果
- K取值:5,10,数据越少k取越大
3.3 常见错误
- 90%的超级好的结果是由于Bug造成的,最可能的原因是由于验证集被污染了
3.3.1 验证集有来自于训练集的样本
- 原始数据集样本重复
- 数据合并时经常发生
3.3.2 信息泄漏
- 常发生于非独立同分布(IID)的数据,验证集中的数据已经在训练集中出现过了
- eg:用未来预测过去
文章出处登录后可见!
已经登录?立即刷新
