最优二叉搜索树(Optimal Binary Search Tree)
- 前言
如果有序数组或有序表中的各个元素查找概率相等,那么采用二叉搜索树(BST)进行折半查找,性能最优。如果有序表中各个记录的查找概率不相等,情况又如何呢?
先看一个具体例子。已知有序表keys, 同时给出各个元素的查询频率,注意到各个元素的查询频率不相同。要求在此条件下,构造出最优搜索二叉查找树。
keys[] = {10, 12, 20},
freq[] = {34, 8, 50}
如果各个元素概率相等,在此基础上,构造二叉搜索树,结果为一颗平衡搜索树。
12
/ \
10 20
考虑各个元素的查找概率和二叉树的不同形式,可以构造五颗不同的二叉搜索树,最优二叉搜索树则是带权路径最小的的和:
10 12 20 10 20
\ / \ / \ /
12 10 20 12 20 10
\ / / \
20 10 12 12
I II III IV V
分别对5种形式的二叉搜索树的带权路径和进行计算,采用列表的形式储存计算结果,则得到下述列表形式,
| 二叉树编号 | 带权路径和 | 备注 |
|---|---|---|
| I | =>34+8*2+50*3=200 | |
| II | =>8+34*2+50*2=176 | |
| III | =>50+8*2+34*3=168 | |
| IV | =>34+50*2+8*3=158 | |
| V | =>50+34*2+8*3=142 | 最优二叉搜索树 |
可以得到结论,等概率的二叉搜索树的带权路径和为176,并不是最优二叉搜索树,本例子中的最优二叉搜索树为第V种形式。还可以看出,最优二叉搜索树并不一定是深度最小的树,第V种二叉树的深度为3,第II种的普通的二叉搜索树的深度为2,即第V种树的深度比第II中多1,但是其带权路径和保持最小。另外还有一个结论,从本例中并不能明显看出,根节点权值不一定是最大权值节点。
上述两点声明和表述主要是说明,构造最小最优二叉搜索树不能简单采用贪心算法,贪心算法通常把最大权值放在根结点,并且设法降低树的高度,贪心算法并不能保证得到最优二叉搜索树。
- 问题求解
按照惯例,依照《算法导论》中的CRCC方法,采用动态规划方法对最优二叉搜索树问题进行求解。首先需要表征最优问题解的基本结构。
- 表征最优问题解的结构(Characterize the structure of the optimal solution)
考察最优二叉搜索树的任意一颗子树,子树包含某个连续元素:
根据递归特性,子树本身一定属于最优二叉搜索树,结论可以用反证法进行证明,不再赘述。分析对象为这颗子树,对于这颗子树我们可以分为左右子树,(ki…kr-1) 和 (kr+1…kj), 把这两颗子树作为kr的左右子树,相当于原来的子树的每个节点的深度都增加1,同时考虑根节点kr的权值,那么选择r作为根节点的代价为w(i,j)。r可以在区间【i,j】之间进行变化,但是选择的代价都是w(i,j)。
- 递归定义最优解的值(Recursively define the value of the optimal solution)
递归定义可以描述为,在ki…kj元素范围内,尝试所有的可能情况,寻找最优二叉搜索树,在暂时不考虑重复子问题的前提下,问题呈现出穷尽/穷举的特征。
对于任意根节点r,根节点位于【i,j】,定义f(i,j)为此节点r的带权路径和,采用数学语言可以描述问题,
这就是状态转移方程,状态转移方程的递归过程实际上分支递减多叉树,第一层多叉树的分枝树为j-i+1, 随着递归的深入,多叉树的分枝数不断减少。最优解涉及到在整个区间上求最小值,得到最后的递归形式的最优解为,
- 求解最优解的值(Compute the value of the optimal solution)
如果采用递归形式,那么求解最优解的值的关键步骤就是定义递归的终止条件,也可以理解为递归的出口。递归出口存在两种形式:
– i>j,这种情况表明,遍历完左边的关键字后,仍然没有找到关键字的匹配,此情况下,直接返回0
– i==j,这种情况表明,找到了匹配的关键字,直接返回本关键字的频率值即可
再看一个具体的例子,鉴定有四个元素,每个元素出现的频次各不相同,要求构造出最优二叉搜索树,从前面得知,如果有四个元素,那么第一次分支就会出现4叉分支,由于分支比较复杂,我们分几张图加以阐述。

分枝1(Branch 1),分枝1的二叉搜索树的最小路径和为233,右边为二叉搜索树,橙色框内需要代表频率数组元素的下标。肢体的一提的是,每个分枝实际上由两部分组成,这两部分 分别代表二叉搜索树的左右子孩子。简单理解,每个分枝由两个孩子构成(可能存在节点没有孩子节点的情况)。
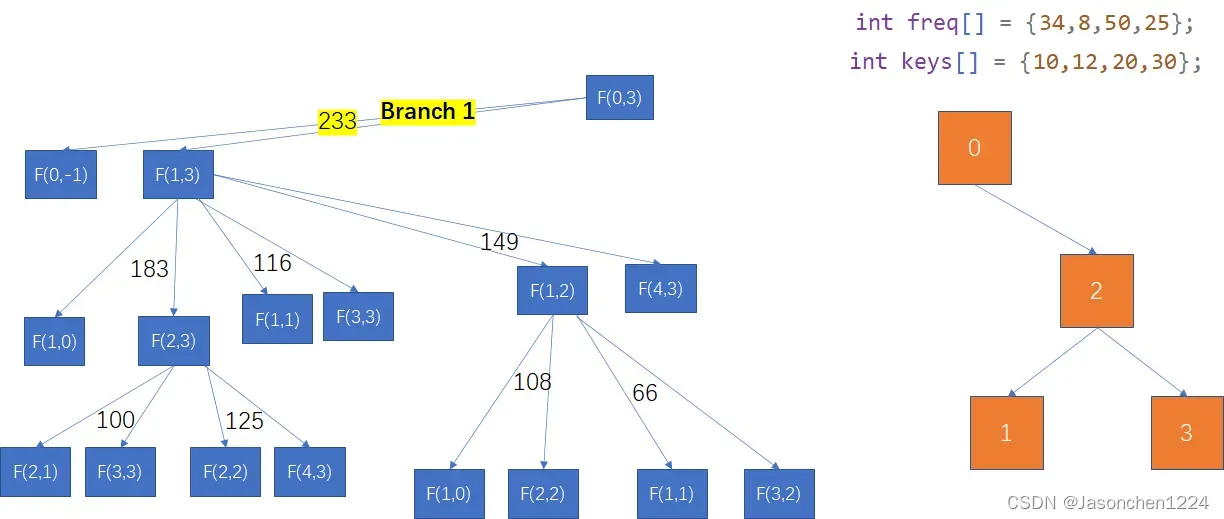
分枝2/分枝3,相同思路,分枝2和分枝3的带权路径和分别为251 和192。左右两边的橙色的二叉树分别对应其相应不同的二叉搜索树。
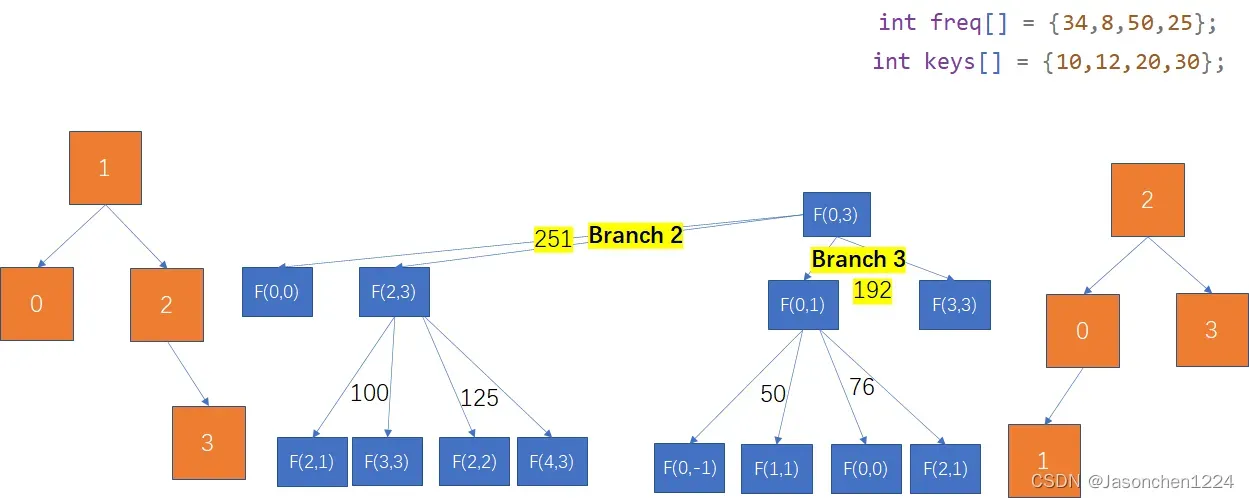
分枝4,分枝4的带权路径和为259,右边的橙色的树代表其带权路径的和。
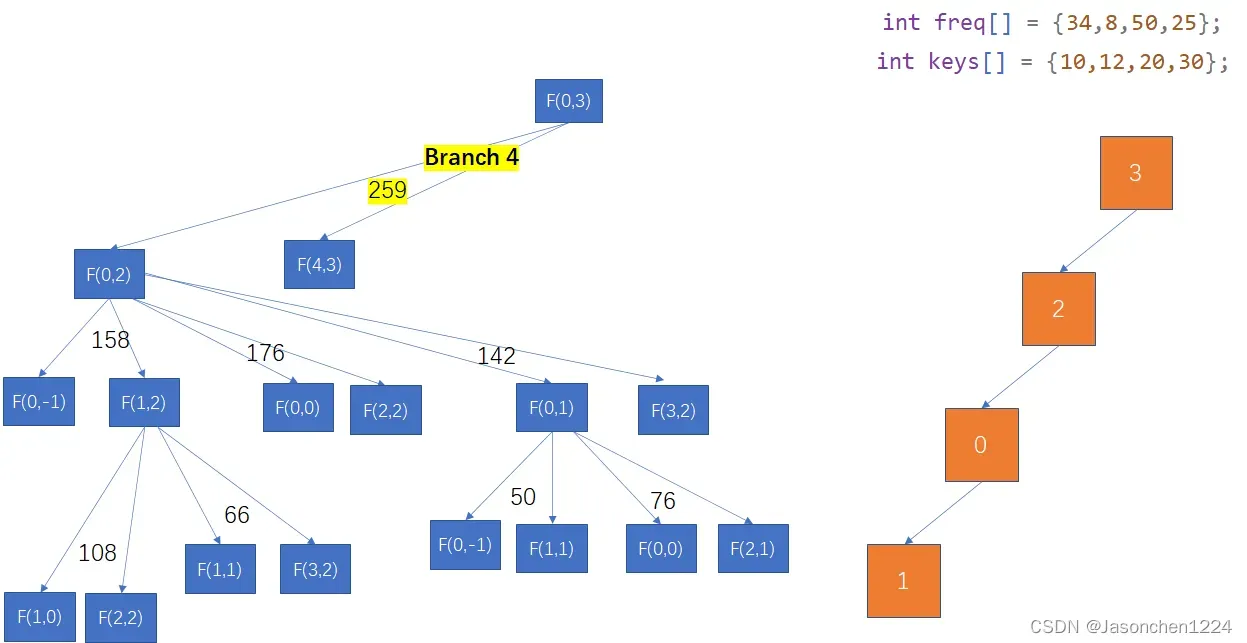
综上,分枝3为本问题的最优二叉搜索树。
动态规划的特征之二就是,不同分支中会出现重叠子问题(overlapping subproblem),如果仔细观察分枝1和分枝4,就会发现F(1,2)子问题都包含再两个分枝当中,这是应用递归记忆的基础,如果没有重复子问题,那么递归记就失去其相应意义。
- 构建具体的解
上述递归仅可以求出最优二叉搜索树的最小带权路径和,但是并无法构造相应的最优二叉搜索树,这就需要追加额外的数组root[n+2][n+2]来记录每个【i,j】区间中的根节点的选择root[i][j]=r。
- 代码实现
3.1 定义头文件
/**
* @file optimal_binary_search_tree.h
* @author your name (you@domain.com)
* @brief
* @version 0.1
* @date 2023-03-31
*
* @copyright Copyright (c) 2023
*
*/
#ifndef OPTIMAL_BINARY_SEARCH_TREE_H
#define OPTIMAL_BINARY_SEARCH_TREE_H
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
/**
* @brief Create the optimal binary search tree on the sorted array
*
* @param freq Frequency array list
* @param i Search start point
* @param j Search end point
* @return int -Return weight of optinal_binary search tree weight
*/
int optimal_BST(int *freq,int i, int j);
/**
* @brief Calculate the sum of frequency list
*
* @param freq Frequency list
* @param i Search start point
* @param j Search end point
* @return int -Return the sume from index=i to index=j
*/
int weight_sum(int *freq, int i, int j);
#endif
3.2 函数的实现
/**
* @file optimal_binary_search_tree.c
* @author your name (you@domain.com)
* @brief
* @version 0.1
* @date 2023-03-31
*
* @copyright Copyright (c) 2023
*
*/
#ifndef OPTIMAL_BINARY_SEARCH_TREE_C
#define OPTIMAL_BINARY_SEARCH_TREE_C
#include "optimal_binary_search_tree.h"
int optimal_BST(int *freq, int i, int j)
{
int r;
int min_value;
int left;
int right;
int c;
if(i>j)
{
return 0;
}
if(i==j)
{
return freq[i];
}
min_value=INT_MAX;
for (r = i; r <= j; r++) // int freq[] = {34,8,50,25};
{
left=optimal_BST(freq,i,r-1);
right=optimal_BST(freq,r+1,j);
c=left+right+weight_sum(freq,i,j);
// int freq[] = {34,8,50,25};
if(c<min_value)
{
min_value=c;
}
}
return min_value;
}
int weight_sum(int *freq, int i, int j)
{
int k;
int sum=0;
for(k=i;k<=j;k++)
{
sum+=freq[k];
}
return sum;
}
#endif
3.3 测试函数
/**
* @file optimal_binary_search_tree_main.c
* @author your name (you@domain.com)
* @brief
* @version 0.1
* @date 2023-03-31
*
* @copyright Copyright (c) 2023
*
*/
#ifndef OPTIMAL_BINARY_SEARCH_TREE_MAIN_C
#define OPTIMAL_BINARY_SEARCH_TREE_MAIN_C
#include "optimal_binary_search_tree.c"
int main(void)
{
int freq[] = {34,8,50,25};
int n=sizeof(freq)/sizeof(int);
int min_value;
min_value=optimal_BST(freq,0,n-1);
printf("The miminum value is %d\n",min_value);
getchar();
return EXIT_SUCCESS;
}
#endif
- 小结
构建二叉搜索树的过程,采用和矩阵链相乘相同的思路,通过直接求解子问题[i,j],从而最终求解全局问题。这个过程中需要特别注意,由于解的结果仅为矩阵中的上三角或下三角,所以需要引入长度的概念,对i和j进行不同的限制,最终达到求解的目的。
参考资料:
- 《Introduction to algorithm, 4ed》
- Optimal Binary Search Tree | DP-24 – GeeksforGeeks
版权声明:本文为博主作者:Jasonchen1224原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/Jasonchen1224/article/details/129898605
