文章目录
- 算法原理
- 斐波那契数列模型
-
- 第n个泰波那契数列
- 三步问题
- 使用最小花费爬楼梯
- 解码方法
- 路径问题
-
- 不同路径
- 不同路径II
- 珠宝的最高价值
- 地下城游戏
从本篇开始总结的是动态规划的一些内容,动态规划是算法中非常重要的一个版块,因此也是学习算法中的一个重点,在学习动态规划前应当要把动态规划的基础知识学习一下
算法原理
动态规划既然是一个新的算法,这个名字也是新名字,那么就要首先明确这个算法的名字代表什么含义
动态规划是什么?
动态规划其实就是dp表中的值所表示的含义
那什么又是dp表?
dp表是解决这类问题中必须要使用的一个内容,通常是借助vector来表示
dp表怎么写出来?
一般来说题目要求中会有一些提示,同时在分析问题的过程中,如果遇到了分析的过程中有重复的子问题,也可以借助这个逻辑写出一个状态转移方程,利用这个状态转移方程就可以填写到dp表中
状态转移方程
状态转移方程就是在动态规划中根据一部分提示找到dp表的填入方法,再根据这个方法就可以借助dp表解决问题,因此状态转移方程是解决问题的关键
斐波那契数列模型
首先用一个比较简单的题目来上手动态规划
第n个泰波那契数列

对于这个题来说,可以用上面的动态规划的方法来处理:
首先创建一个dp表,再从题目中找到状态转移方程,再利用状态转移方程写入dp表,再利用dp表求出要找的数据
class Solution
{
public:
int tribonacci(int n)
{
// 处理边界
if(n==0)
{
return 0;
}
if(n==1 || n==2)
{
return 1;
}
// 创建dp表
vector<int> dp(n+1);
// 初始化dp表
dp[0]=0;
dp[1]=1;
dp[2]=1;
//填入dp表
for(int i=3;i<=n;i++)
{
dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
}
// 返回值
return dp[n];
}
};
三步问题

分析问题:
假设现在有1个台阶,那么小孩跳到这个台阶的方法有1种,直接从地面走到第一个台阶上
假设现在有2个台阶,那么小孩跳到这个台阶的方法有2种,第一种从地面直接走到第二个台阶上,第二种是小孩从地面走到第一个台阶,再从第一个台阶走到第二个台阶上
假设现在有3个台阶,那么小孩跳到这个台阶的方法有4种,第一种直接跳到第三个台阶上,第二种先跳到第一个台阶,再从第一个台阶向第三个台阶跳,而从第一个台阶向第三个台阶跳又有两种,参考有2个台阶的方案,那么总共第二种方法有2种,第三种小孩跳到第二个台阶,再从第二个台阶跳到第三个台阶,因此总共有四种方法
假设现在有4个台阶,那么小孩跳到第四个台阶的方法总共有7种,先让小孩走到第一个台阶,再从第一个台阶走到第四个台阶即可,而小孩走到第一个台阶的方法有1种;也可以先让小孩走到第二个台阶,再从第二个台阶走到第四个台阶,而小孩走到第二个台阶的方法有2种;先让小孩走到第三个台阶,再从第三个台阶直接到第四个台阶,而直接让小孩走到第四个台阶的方法有4种,因此上面的这些总计是7种
假设现在有5个台阶,那么小孩跳到第五个台阶的方法有13种,先让小孩跳到第二个台阶,再从第二个台阶直接到第五个台阶…
因此规律就找到了,其实就是一个斐波那契数列的变形问题,利用上面的例题的思路就可以解决这个问题
class Solution
{
public:
int waysToStep(int n)
{
vector<long long> dp(n+4);
dp[0]=0;
dp[1]=1;
dp[2]=2;
dp[3]=4;
for(int i=4;i<=n;i++)
{
dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
dp[i] %= 1000000007;
}
return dp[n];
}
};
使用最小花费爬楼梯

此题也是动态规划中的一个典型题,这里从两个角度来看这道题
从最开始的介绍中可以知道,对于动态规划的问题来说,关键是dp[i]的意义和状态转移方程,在解决问题的过程中要优先对这两个部分进行思考和解决,那么两个不同的dp[i]的角度来看这个题
首先从第一个角度来看:
如果这里的dp[i]表示的是,上到第i个台阶需要花费多少钱:
那么可以这样思考问题,要知道上到第i个台阶需要多少钱,就必然要知道上到第i-1个台阶要花多少钱,再用这个钱加上上第i-1个台阶要花多少钱,由于一次可以上两个台阶,因此也要知道上到第i-2个台阶需要多少钱和上这个台阶需要多少钱,再比较一下从第i-1个台阶上划算还是从第i-2个台阶上划算,比较后就可以得到dp[i]的值,因此状态转移方程就很容易得到了
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
此时注意一下边界初始化问题:在第0和第1个台阶是不需要花钱的,于是初始化为0即可,代码也可以很好的实现出来
class Solution
{
public:
int minCostClimbingStairs(vector<int>& cost)
{
vector<int> dp(cost.size()+1);
dp[0]=0;
dp[1]=0;
for(int i=2;i<=cost.size();i++)
{
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
return dp[cost.size()];
}
};
以上为第一种思考的方式,dp[i]对应的意义还有其他,这里还可以理解为从第i个位置上到最顶上需要的花费,因此这里也可以借助这个意义来解决
那如果要求从第i个台阶上到顶端要花多少钱,需要知道从第i个台阶一次上一个台阶还是一次上两个台阶比较划算,因此这里又需要知道i+1和i+2的值,根据这两个的值决定一次上一个台阶还是上两个台阶,因此状态转移方程也可以得出来了:
dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i]);
那么代码的实现也可以得出:
class Solution
{
public:
int minCostClimbingStairs(vector<int>& cost)
{
int n=cost.size();
vector<int> dp(n);
dp[n-1]=cost[n-1];
dp[n-2]=cost[n-2];
for(int i=n-3;i>=0;i--)
{
dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i]);
}
return min(dp[0],dp[1]);
}
};
解码方法

class Solution
{
public:
int numDecodings(string s)
{
// 处理特殊情况
if(s[0] == '0')
return 0;
if(s.size() == 1)
return 1;
// 状态转移方程 dp[i] = dp[i - 1] + dp[i - 2]
int n = s.size();
vector<int> dp(n, 0);
// 初始化问题
if(s[0] >= '1' && s[0] <= '9')
dp[0] = 1;
else
dp[0] = 0;
if(s[1] >= '1' && s[1] <= '9')
dp[1] += 1;
int a = s[0] - '0', b = s[1] - '0';
if((a * 10 + b) >= 10 && (a * 10 + b) <= 26)
dp[1] += 1;
for(int i = 2; i < n; i++)
{
if(s[i] >= '1' && s[i] <= '9')
dp[i] += dp[i - 1];
int a = s[i - 1] - '0', b = s[i] - '0';
if(a * 10 + b >= 10 && a * 10 + b <= 26)
dp[i] += dp[i - 2];
}
return dp[n - 1];
}
};
路径问题
不同路径

class Solution
{
public:
int uniquePaths(int m, int n)
{
// 建表
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
// 状态转移方程 dp[i, j] = dp[i - 1, j] + dp[i, j - 1];
// 填表
dp[0][1] = 1;
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
return dp[m][n];
}
};
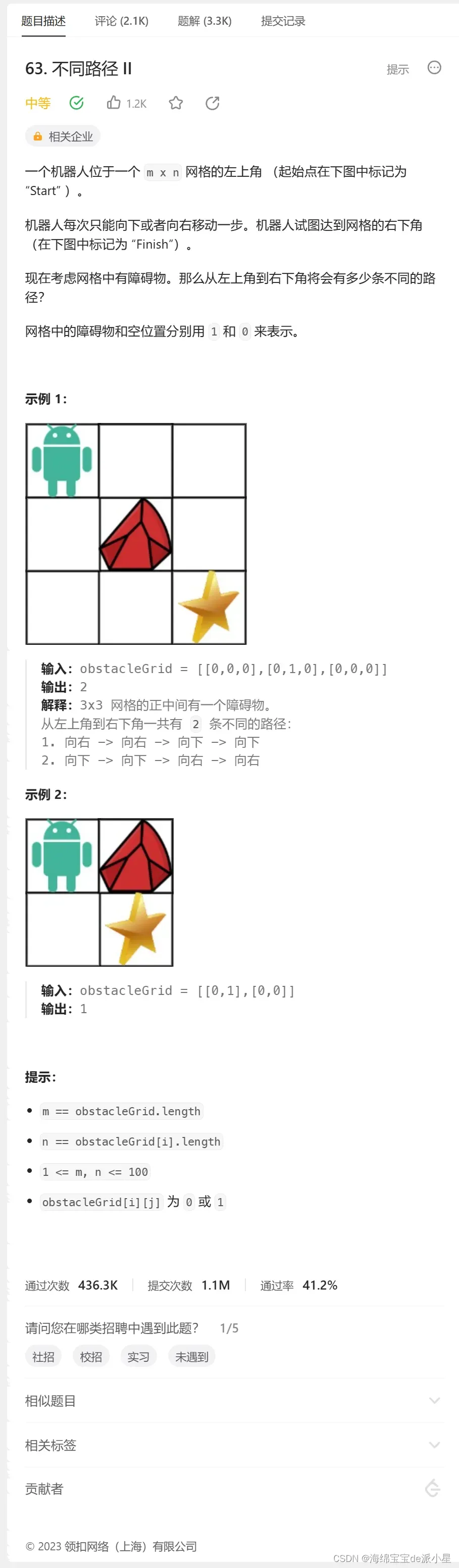
不同路径II
class Solution
{
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid)
{
// 1.建表
int m = obstacleGrid.size(), n = obstacleGrid[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
// 2.初始化
dp[0][1] = 1;
// 3.填表
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
if(obstacleGrid[i - 1][j - 1] == 0)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
// 4.返回结果
return dp[m][n];
}
};
珠宝的最高价值

class Solution
{
public:
int jewelleryValue(vector<vector<int>>& frame)
{
// 状态转移方程:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i - 1][j - 1]
// 1. 建表
int m = frame.size(), n = frame[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
// 2. 初始化
dp[0][1] = 0;
// 3. 填表
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i - 1][j - 1];
// 4. 返回值
return dp[m][n];
}
};
地下城游戏

class Solution
{
public:
int calculateMinimumHP(vector<vector<int>>& dungeon)
{
int n = dungeon.size(), m = dungeon[0].size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1, INT_MAX));
dp[n][m - 1] = dp[n - 1][m] = 1;
for (int i = n - 1; i >= 0; --i)
{
for (int j = m - 1; j >= 0; --j)
{
int minn = min(dp[i + 1][j], dp[i][j + 1]);
dp[i][j] = max(minn - dungeon[i][j], 1);
}
}
return dp[0][0];
}
};
版权声明:本文为博主作者:海绵宝宝de派小星原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/qq_73899585/article/details/132838724
