图论入门（完结）

更新线

• 图的基本概念（已更）
• 图的存储结构（邻接矩阵、邻接表、链式前向星）（已更）
• 图的遍历（深度优先、广度优先）（已更）
• 一笔画问题（欧拉回路，已更）
• 哈密顿路问题（已更）
• 最短路径（已更）
• 最小生成树(已更)

图论简介及相关概念

图 是一个二元组，其中是非空集，称为点集 ，对于中的每个元素，我们称其为顶点或节点，简称点，为各结点之间边的集合，称为边集
常用 表示图

• 当都是有限集合时，称为有限图
• 当或都是有限集合时，称为无限图

图有多种，包括无向图，有向图 ，混合图 ，带权图 等

举个例子

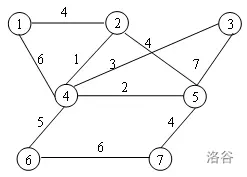
无向图专业术语

1. 两个顶点之间如果有边连接，那么就视为两个顶点相邻
2. 路径：相邻顶点的序列
3. 圈：起点和终点重合的路径
4. 连通图：任意两点之间都有路径连接的图
5. 度：顶点连接的边数叫做这个顶点的度
6. 树：没有圈的连通图
7. 森林：没有圈的非连通图

有向图专业术语

1. 在有向图中，边是单向的：每条边所连接的两个顶点是一个有序对，他们的邻接性是单向的
2. 有向路径：相邻顶点的序列
3. 有向环：一条至少含有一条边且起点和终点相同的有向路径
4. 有向无环图：没有环的有向图
5. 度：一个顶点的入度与出度之和称为该顶点的度
   1.入度：以顶点为弧头的边的数目称为该顶点的入度
   2.出度：以顶点为弧尾的边的数目称为该顶点的出度

图的存储方式

1.邻接矩阵

方法：对于一个有的顶点的图而言，可以使用的二维数组表示表示的是顶点与顶点的关系。如果顶点和顶点之间有边相连，如果顶点和顶点之间无边相连，，对于无向图：

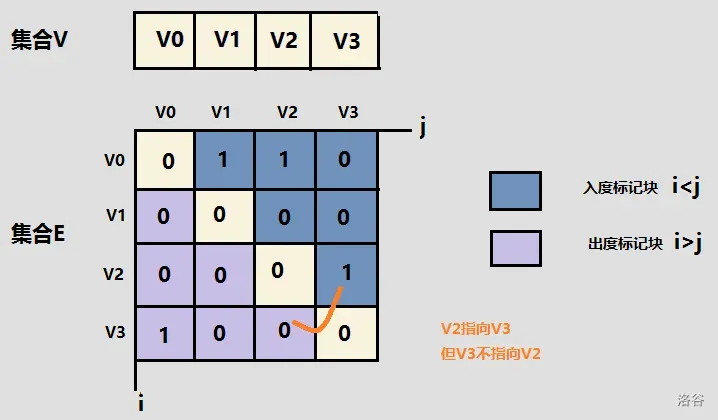
bool adj[MAXN][MAXN];
scanf("%d %d", &n , &m);
for (int i = 1 ; i <= m ; i ++) {
	int u , v;
	scanf("%d %d", &u , &v);
	adj[u][v] = 1;
	adj[v][u] = 1;	
} 

2.邻接表

方法：使用一个支持动态增加元素的数据结构构成的数组，如 <> 来存边，其中存储的是点的所有出边的相关信息终点、边权等

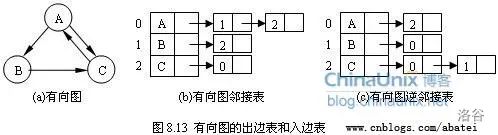
struct node{
	vector<int> v;
}a[MAXN];

for (int i = 1 ; i <= m ; i ++) {
	int u , v;
	scanf("%d %d", &u , &v);
	a[u].v.push_back(v);
	a[v].v.push_back(u);	
} 
return 0;

3.链式前向星

方法:

对于这样一张有向图：

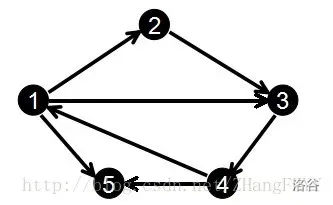
1 2  
2 3  
3 4  
1 3  
4 1  
1 5  
4 5

对于邻接表来说是这样的：

1 -> 2 -> 3 -> 5
2 -> 3
3 -> 4
4 -> 1 -> 5
5 -> ^
对于链式前向星来说是这样的：
edge[0].to = 2; edge[0].next = -1; head[1] = 0;
edge[1].to = 3; edge[1].next = -1; head[2] = 1;
edge[2].to = 4; edge[2],next = -1; head[3] = 2;
edge[3].to = 3; edge[3].next = 0; head[1] = 3;
edge[4].to = 1; edge[4].next = -1; head[4] = 4;
edge[5].to = 5; edge[5].next = 3; head[1] = 5;
edge[6].to = 5; edge[6].next = 4; head[4] = 6;
简化后：1 -> 5 -> 3 -> 2

核心代码：

struct edge{
	int to , nxt , w;
};
edge a[MAXN];
void add(int u , int v , int w) {
	a[cnt].w = w;
	a[cnt].to = v;
	a[cnt].nxt = head[u];
	head[u] = cnt ++;
}

图的遍历

（内置芝士）什么是图的遍历：从图中的某个顶点出发，按某种方法对图中的所有顶点访问且仅访问一次。为了保证图中的顶点在遍历过程中仅访问一次，要为每一个顶点设置一个访问标志

1.有向图的dfs

题目大意：

给定一个有向图，有个顶点，条边，顶点从依次编号，求出字典序最小的深度优先搜索顺序

总体思路：

利用邻接表存储点的关系，将点放入里搜索与之相邻但未被遍历过的点
核心代码如下:

void dfs(int k) {
   if (vis[k]) return;
   vis[k] = 1;
   printf("%d ", k);
   for (set<int>:: iterator it = st[k].begin() ; it != st[k].end() ; it ++) {
   	dfs(*it);
   }
}
for (int i = 1 ; i <= m ; i ++) {
   int u , v;
   scanf("%d %d", &u , &v);
   st[u].insert(v);
} 
dfs(1);
for (int i = 1 ; i <= n ; i ++) {
   if (!vis[i]) dfs(i);
}

2.有向图的bfs

题目大意：

给定一个有向图，有个顶点，条边，顶点从…依次编号，求出字典序最小的宽度优先搜索顺序

思路：

利用邻接表存储点的关系，将点放入里搜索与之相邻但未被遍历过的点
核心代码如下：

void bfs(int k) {
   q.push(k);
   while(!q.empty()) {
   	int x = q.front();
   	q.pop();
   	if (vis[x]) continue;
   	vis[x] = 1;
   	printf("%d ", x);
   	for (set<int>:: iterator it = st[x].begin() ; it != st[x].end() ; it ++) {
   		q.push(*it);
   	}
   }
}
for (int i = 1 ; i <= m ; i ++) {
   int u , v;
   scanf("%d %d", &u , &v);
   st[u].insert(v);	
} 
bfs(1);
for (int i = 1 ; i <= n ; i ++) {
   if (!vis[i]) bfs(i);
}

3.无向图的bfs

题目大意：

一个无向图，从指定顶点出发进行，求遍历得到的顶点序

总体思路：

利用邻接矩阵存储边(每一层要从小到大排序，矩阵方便操作)，将点放入里搜索与之相邻但未被遍历过的点
核心代码如下：

void bfs() {
	q.push(rt);
	while(!q.empty()) {
		int x = q.front();
		q.pop();
		if (vis[x]) continue;
		vis[x] = 1;
		printf("%d ", x);
		for (int i = 1 ; i <= n ; i ++) {
			if (adj[x][i]) {
				q.push(i);
			}
		}
	}
}
for (int i = 1 ; i <= m ; i ++) {
	int u , v;
	scanf("%d %d", &u , &v);
	adj[u][v] = 1;
	adj[v][u] = 1;	
} 

一笔画问题（欧拉路）

Ps：欧拉路指的是：存在这样一种图，可以从其中一点出发，不重复地走完其所有的边如果欧拉路的起点与终点相同，则称之为欧拉回路
需满足条件：

1. 图是连通的，若不连通不可能一次性遍历所有边
2. 对于无向图：有且仅有两个点，与其相连的边数为奇数，其他点相连边数皆为偶数；或所有点皆为偶数边点。对于两个奇数点，一个为起点，一个为终点。起点需要出去，终点需要进入，故其必然与奇数个边相连
3. 如果存在这样一个欧拉路，其所有的点相连边数都为偶数，那说明它是欧拉回路
4. 对于有向图：除去起点和终点，所有点的出度与入度相等。起点出度比入度大1，终点入度比出度大1。若起点终点出入度也相同，则为欧拉回路

利用求一笔画路径

题目大意：

根据一笔画的两个定理，如果寻找欧拉回路，对任意一个点执行深度优先遍历；找欧拉路，则对一个奇点执行，时间复杂度为，为边数，是点数

总体思路：

即把奇点作为起点放入搜索,每搜索到一个相邻的点即把这条边删掉，若所有边都遍历到了，输出答案
核心代码如下：

void dfs(int k , int id) {
   ans[id] = k;
   bool f = 1;
   for (int i = 1 ; i <= n ; i ++) {
   	for (int j = 1 ; j <= m ; j ++) {
   		if (a[i][j]) {
   			f = 0;
   			break;
   		}
   	}
   }
   if (f) {
   	for (int i = 1 ; i <= id ; i ++) {
   		printf("%d ", ans[i]);
   	}
   	exit(0);
   }
   for (int i = 1 ; i <= n ; i ++) {
   	if (a[k][i]) {
   		a[k][i] = 0;
   		a[i][k] = 0;
   		dfs(i , id + 1);
   		a[k][i] = 1;
   		a[i][k] = 1;
   	}
   }
} 

暴力求解哈密顿图

思路：利用邻接表存储边的关系，枚举1~作为起点的情况，然后每搜到一种情况便把加即可

int dfs(int k , int cnt) {
	if(cnt == n) return 1;
	int res = 0;
	for (int i = 1 ; i <= h[k][0] ; i ++) {
		if (!vis[h[k][i]]) {
			vis[h[k][i]] = 1;
			res += dfs(h[k][i] , cnt + 1);
			vis[h[k][i]] = 0;
		}
	}
	return res;
} 
for (int i = 1 ; i <= n ; i ++) {
	vis[i] = 1;
	ans += dfs(i , 1);
	vis[i] = 0;
}

最短路问题

最短路径问题是图论研究中的一个经典算法问题， 旨在寻找图由结点和路径组成的中两结点之间的最短路径。
例如：

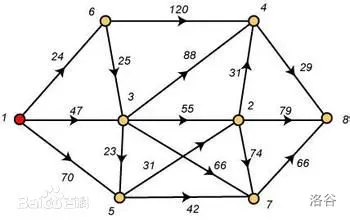
1.

佛洛伊德是最简单的最短路径算法，可以计算图中任意两点间的最短路径。时间复杂度为，适用于出现负边权的情况

算法描述：

1. 初始化：
   点、如果有边相连，则，如果不相连，则

2. 核心代码

for(int k = 1 ; k <= n ; k ++) {
   for(int i = 1 ; i <= n ; i ++) {
      for(int j = 1 ; j <= n ; j ++) {
         if(F[i][j] > F[i][k] + F[k][j]) {
            F[i][j] = F[i][k] + F[k][j];
         }  
      }
   }
}	

3. 算法解释：

得出的就是任意起点到任意终点的最短路径
– 动态规划以”途径点集大小”为阶段
– 决策需要枚举中转点，不妨考虑也以中转点集为阶段
– 表示”可以经过标号的点中转时”从到的最短路
– ，为前面定义的邻接矩阵
– = { , + }
– 这一维空间可以省略，变成
– 由于是的阶段循环，所以循环必须要放在最外层

4. 使用输出最短路径：

算法输出路径也是采用记录前驱点的方式。因为是计算任意两点间最短路径的算法，记录从到的最短路径值。故我们定义为一个二维数组，记录从到的最短路径中，的前驱点是哪一个，递归还原路径

• 为 0，输入相连边时，重置相连边尾结点的前驱若有无向边：，
• 更新若最短路有更新，那么
• 递归输出指两点，的最短路，先输出起点，再将终点放入递归，输出的所有点。

核心代码：

void floyd() {
	for (int k = 1 ; k <= n ; k ++) {
		for (int i = 1 ; i <= n ; i ++) {
			for (int j = 1 ; j <= n ; j ++) {
				if (dp[i][k] + dp[k][j] < dp[i][j]) {
					dp[i][j] = dp[i][k] + dp[k][j];
					pre[i][j] = pre[k][j];
				}
			}
		}
	} 
}
void print(int x) {
	if (pre[s][x] == 0) return;
	print(pre[s][x]);
	printf(" %d", x);
}

2.

主要方法：

• 分成两组：已经确定最短路、尚未确定最短路
• 从第2组中选择路径长度最短的点放入第1组并扩展
• 本质是贪心，只能应用于正权图
• 普通的算法
• 堆优化的算法

引入概念——松弛操作：

• 原来用一根橡皮筋直接连接、两点，现在有一点k，使得比的距离更短，则把橡皮筋改为 ，这样橡皮筋更加松弛。
• 代码实现：

算法描述：

设起点为，表示从指定起点到的最短路径，为的前驱，用来输出路径

1.初始化

；

；
；；；

2. 松弛次

1. 在没有被访问过的点中找一个相邻顶点k，使得是最小的；
2. 标记为已确定的最短路;
3. 用循环更新与k相连的每个未确定最短路径的顶点(所有未确定最短路的点都松弛更新)

3.算法结束

dis为到的最短路距离；为的前驱结点，用来输出路径

让我们来看一组动画 （不动的动画）

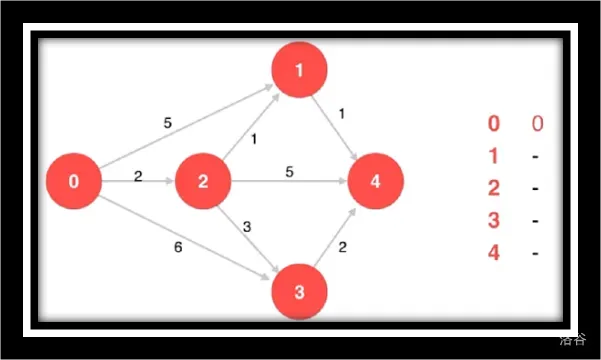
原始图

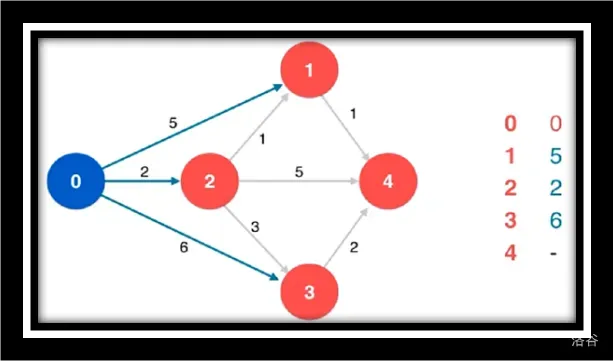
初始化

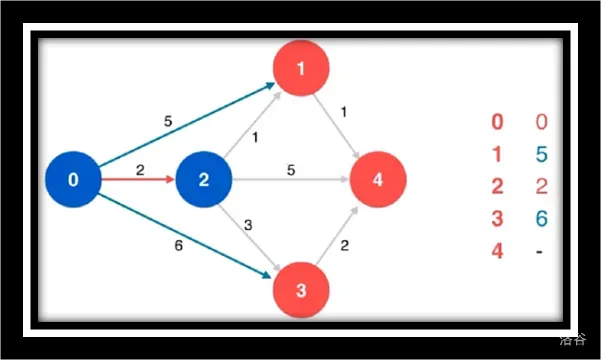
寻找源点相邻的最短路

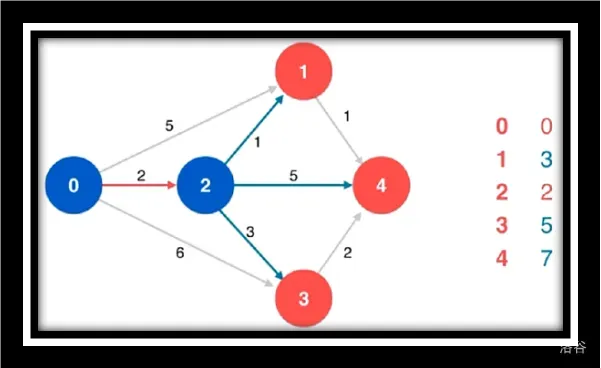
松弛源点到1/4/3

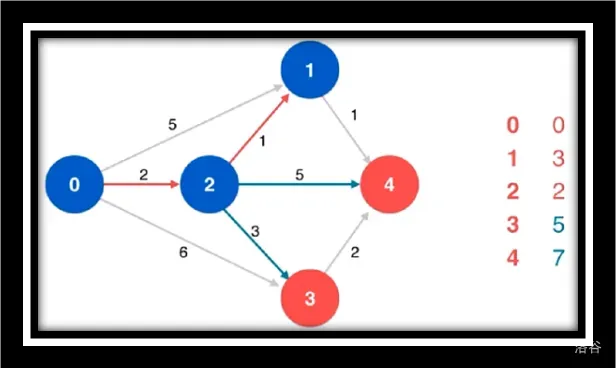
寻找源点到1/4/3的最短路

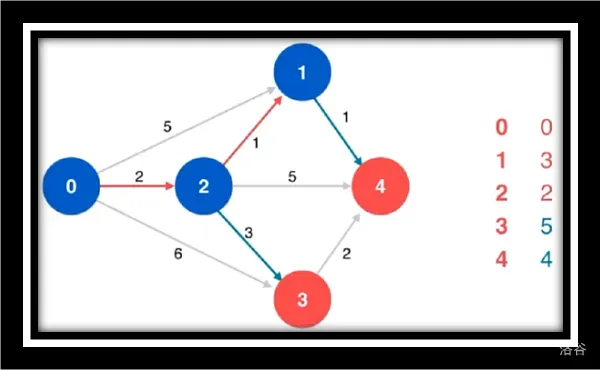
松弛源点到4

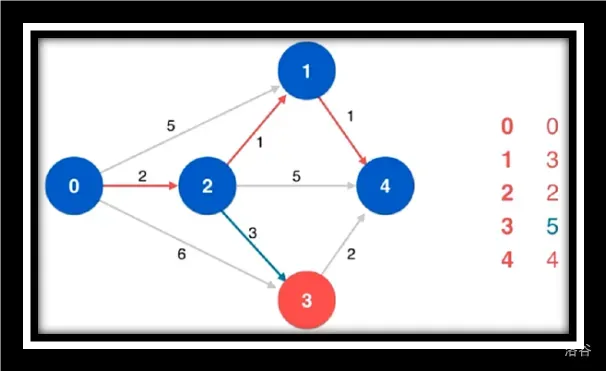
寻找源点到4的最短路由于点4没有相邻点故不作松弛操作

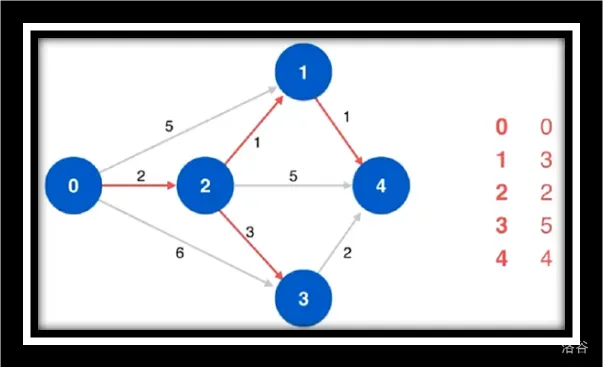
寻找剩余未访问点3松弛源点到4并未更改最短路

最后奉上本人的代码（优化后） ：

struct edge{
   int to , nxt , w;
}a[MAXN];
void add(int u , int v , int w) {
   a[++ cnt].w = w;
   a[cnt].to = v;
   a[cnt].nxt = head[u];
   head[u] = cnt;
}
struct node{
   int id , w;
   node(int iid , int ww) {
   	id = iid;
   	w = ww;
   }
   friend bool operator<(node x , node y) {
   	return x.w > y.w;
   }
};
priority_queue<node> q;
void dijkstra() {
   memset(dis , 0x3f , sizeof(dis));
   dis[s] = 0;
   q.push(node(s , 0));
   while(!q.empty()) {
   	int u = q.top().id;
   	q.pop();
   	if (vis[u]) continue;
   	vis[u] = 1;
   	for (int i = head[u] ; i ; i = a[i].nxt) {
   		int v = a[i].to , w = a[i].w;
   		if (dis[v] > dis[u] + w) {
   			dis[v] = dis[u] + w;
   			q.push(node(v , dis[v]));
   		}
   	}
   }
}

3.

• 算法：对每条边执行更新，迭代次
• 具体操作是对图进行最多次松弛操作，每次操作对所有的边进行松弛，为什么是次操作呢？这是因为我们输入的边不一定是按源点由近至远，万一是由远至近最坏情况就得次
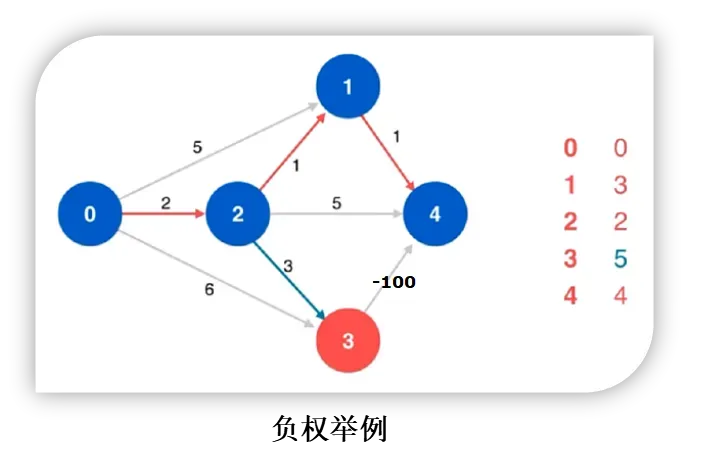
• 可以应用于负权图
• 预计时间复杂度：

非本人代码（不想打了）：

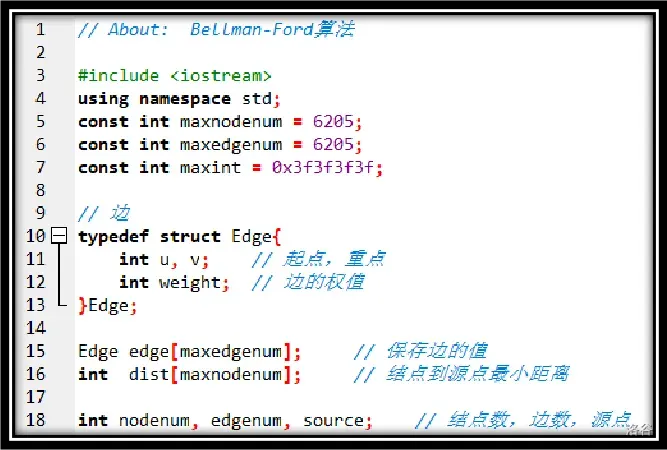
想都不用想就知道有多慢

所以，我们引入了一个新的算法——

4.

• 等于队列优化的算法
• 本质上还是迭代——每更新一次就考虑入队
• 稀疏图上，稠密图上退化到
• 可以应用于有向负权图
• 算法实现：它采用了队列和松弛技术。先将源点加入队列。然后从队列中取出一个点(此时该点为源点)，对该点的邻接点进行松弛，如果该邻接点松弛成功且不在队列中，则把该点加入队列。如此循环往复，直到队列为空，则求出了最短路径
• 判断有无负环：如果某个点进入队列的次数超过次则存在负环 ( 存在负环则无最短路径,如果有负环则会无限松弛,而一个带个点的图至多松弛次)

你理解了吗？

bool vis[MAXN];
struct edge{
	int to , w , nxt;
}a[MAXN];
void add(int u , int v , int w) {
	a[++ cnt].w = w;
	a[cnt].to = v;
	a[cnt].nxt = head[u];
	head[u] = cnt;
}
struct node {
	int id , w;
	node(int iid , int ww) {
		id = iid;
		w = ww;
	}
};
queue<node> q;
int SPFA() {
	memset(dis , 0x3f, sizeof(dis));
	dis[s] = 0;
	q.push(node(s , 0));
	while(!q.empty()) {
		int u = q.front().id;
		q.pop();
		vis[u] = 0;
		for (int i = head[u] ; i ; i = a[i].nxt) {
			int v = a[i].to , w = a[i].w;
			if (dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w;
				if (!vis[v]) {
					vis[v] = 1;
					q.push(node(v , dis[v]));
				}
			}
		}
	}
	return 1;
}

最小生成树

引入：树有这样一个定理：个点用条边连接成一个连通块，形成的图形只可能是树，叫做生成树！因此，一个有个点的连通图，边一定条

概念：最小生成树 简称求带权无向图的一棵子树，包含个点，条边，边权之和最小

算法

算法思路：

1. 以任意一个点为基准点
2. 节点分为两组：
   1）在上到基准点的路径已经确定的点
   2）尚未在中与基准点相连的点
3. 不断从第2组中选择与第1组距离最近的点加入第1组，类似于，本质也是贪心，

算法描述：

总体思想：也使用“蓝白点”思想，白点代表已进入最小生成树的点，蓝点代表未进入最小生成树的点

以1为起点生成最小生成树，表示蓝点与白点相连的最小边权， 表示最小生成树的权值之和

初始化：;

寻找,最小的蓝点;
②将标记为白点;
③;
④与白点相连的所有蓝点v(可暴力枚举，更好的是求的)

算法结束：MST即为最小生成树的权值之和

这次ppt的图片不是一个整体，太难盗图了，就直接上代码吧

void Prim() {
	for (int i = 1 ; i <= n ; i ++) d[i] = 0x3f3f3f3f3f3f;
	d[1] = 0;
	q.push(node(1 , 0));
	while(!q.empty()) {
		int u = q.top().id;
		q.pop();
		if (vis[u]) continue;
		vis[u] = 1;
		for (int i = head[u] ; i ; i = a[i].nxt) {
			ll v = a[i].to;
			ll w = a[i].w;
			if (w < d[v] && !vis[v]) {
				d[v] = w;
				q.push(node(v , d[v]));
			}
		}
		MST += d[u];
	}
}

算法

算法思路：

1. 利用并查集，起初每个点各自构成一个集合
2. 所有边按照边权从小到大排序，依次扫描
3. 若当前扫描到的边连接两个不同的点集就合并
4. 本质也是贪心，
5. 与Prim算法相比，没有基准点，该算法是不断选择两个距离最近的集合进行合并的过程

算法描述：

初始化

①写出并查集三件套
②将边按权值大小排序

$(b)

①两个点的祖先不是同一个,将两个点合并，并累加权值;
②如果图已经联通，即跳出

©算法结束：即为最小生成树的权值之和。

依旧很难盗图，无语

void kruscal() {
	int tot = 0;
	for (int i = 1 ; i <= m ; i ++) {
		if (UnionSet(a[i].u , a[i].v)) {
			MST += a[i].w;
			tot ++;
			if (tot == n) return;
		}
	}
}