图论(2)——道路与回路

文章目录

• 一、 道路与回路
• • 有向道路/有向回路
  • 无向图的道路及道路的长度
  • 联通图
  • 弦
  • • 定义
    • 定理
    • 极长初级道路
    • 扩大初级道路法
  • 二分图
  • • 定义
    • 定理
  • 图的性质
  • 两点间距离,割点,割边
• 二、欧拉道路与回路
• • 定义
  • 欧拉定理
  • 应用
• 三、哈密顿道路与回路
• • 定义(哈密顿图)
  • 回路-引理
  • 哈密顿道路与回路-充分性定理1
  • 闭合图
  • 哈密顿道路与回路-充分性定理2
  • 例子
  • 哈密顿道路与回路-必要性定理

一、 道路与回路

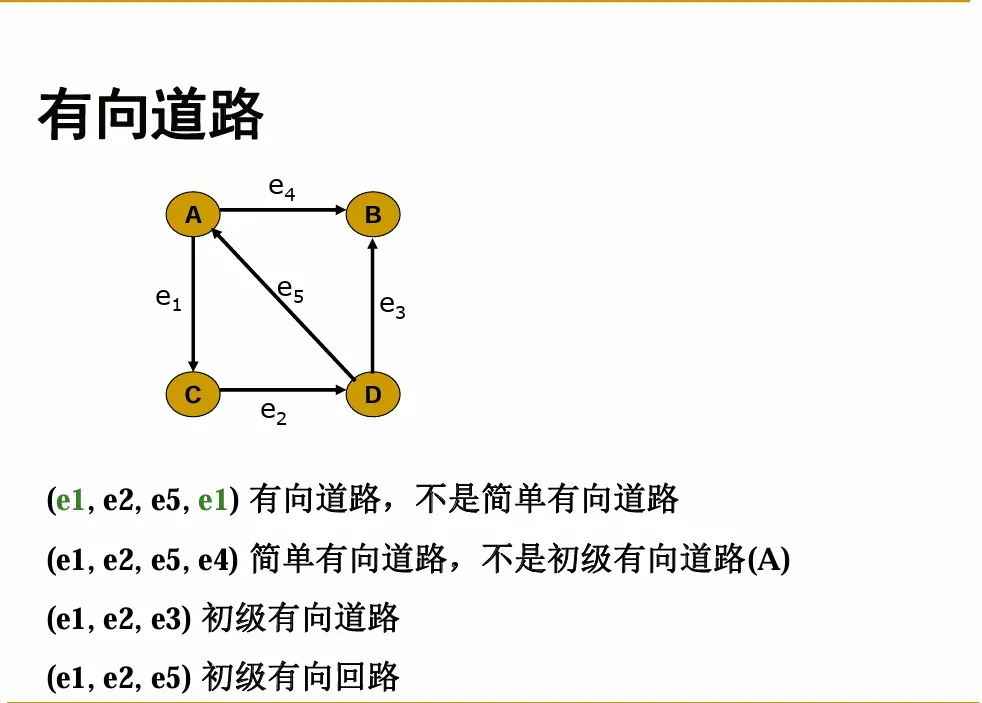
有向道路/有向回路

• 如果P中的边没有重复出现，则分别称为简单 (simple)有向道路和简单有向回路
• 进而, 如果P中结点也不重复出现, 又分别称它们是初级(primary)有向道路和初级有向回路, 简称为路和回路
• 显然,初级有向道路path(回路circuit)一定是简单有向道路(回路)

我的理解:这里指结点不重复出现,指的是1个结点不作为起点/终点两次及以上

无向图的道路及道路的长度

无向图G=(V, E)中，若点边交替序列满足的两个端点, 则称P 是G中的一条链或道路. 如果, 则称P是G中的一 个圈或回路，其长度为边数（q-1）

如果P中没有重复出现的边, 称之为简单道路或简单回路,
若其中结点也不重复,又称之为初级道路或初级回路 ^155bcf

联通图

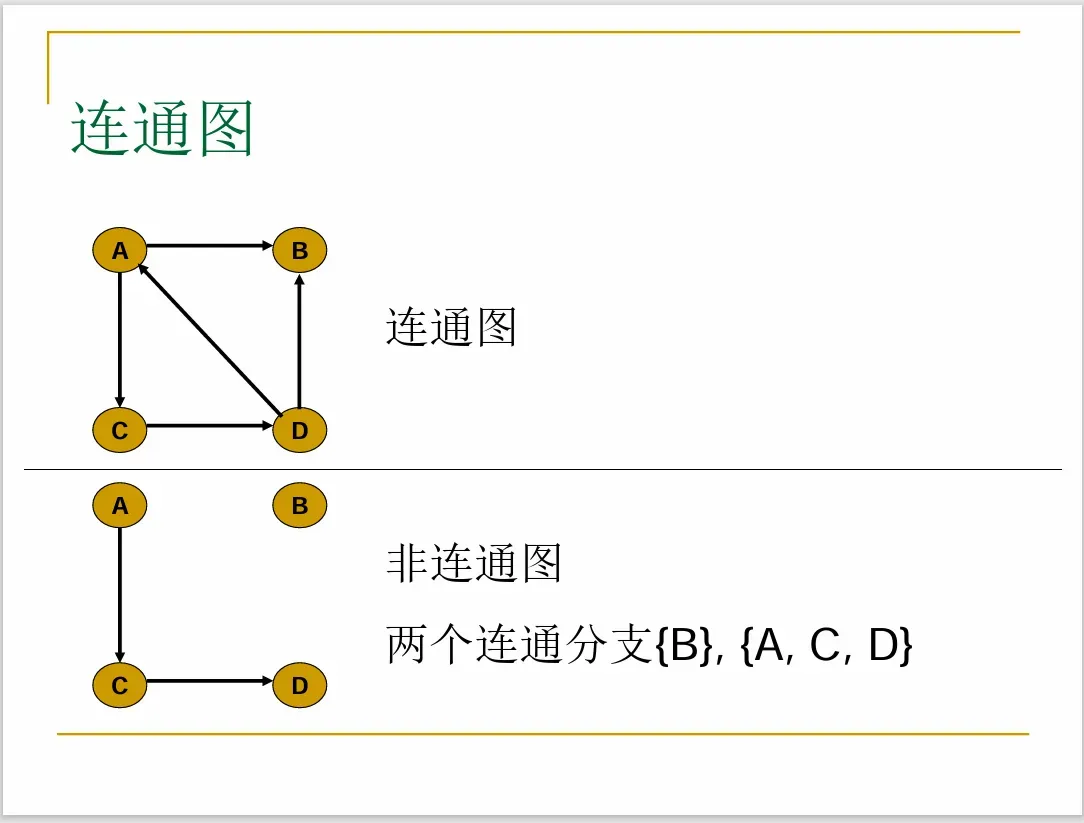
• G是无向图: 若G的任意两结点之间都存在道路, 就称G是连通图, 否则称为非连通图
• 如果G是有向图, 不考虑其边的方向, 即视为无向图; 若它是连通的, 则称G是连通图
• 若连通子图H不是G的任何连通子图的真子图, 则称H是G的极大连通子图或称连通支
• 显然G的每个连通支都是它的导出子图

弦

定义

设C是简单图G中含结点数大于3的一个初级回路，如果结点vi和vj在C中不相邻，而边 (vi,vj)E(G)，则称(vi,vj)是C的一条弦。该回路也称为带弦回路（chordal circuit）。

定理

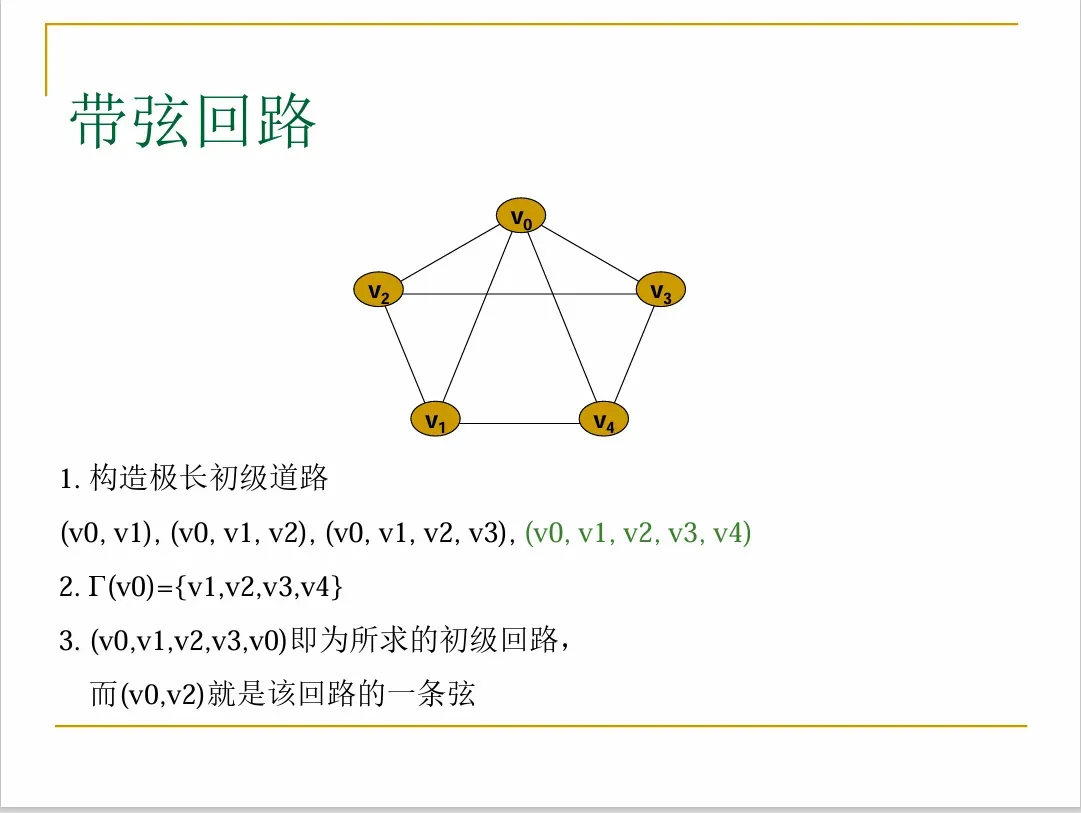
若对简单图G中每一个vkV(G)，都有d(vk)≥3， 则G中必含带弦的回路。
证明: 在G中构造一条极长（不可外延）的初级道路 （不可内延）。
由于P是 极长的初级道路，所以v0和vl的邻接点都在该道路P上。
由已知条件，d()≥3，不妨设Γ()={ }, 其 中1<j<k, 这时()是一条初级回路，而(v0, )就是该回路中的一条弦。

极长初级道路

在无向简单图G=中, E≠∅, 设Γ1=v0,v1,…,vl为G中一条初级道路,若路径的两个端点v0和vl 不与初级道路本身以外的任何结点 相邻, 这样的初级道路称为极长初级道路
(有向图中, 初级道路起点的前驱, 终点的后继, 都在初级道路本身上)

扩大初级道路法

任何一条初级道路, 如果不是极长初级道路, 则至少有一个端点与初级道路本身以外的结点相邻, 则将该结点及其相关联的边扩到新的初级道路中来, 得到更新的初级道路。继续上述过程, 直到变成极长初级道路为止.

二分图

定义

设G=(V,E)是无向图，如果V(G)可以划分为子 集X和Y，使得对所有的e=(u,v)E(G), 都有u 和v分属于X和Y，则称G是二分图。

定理

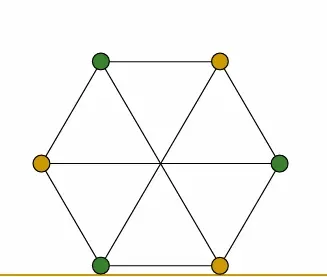
• 含有K3子图的图一定不是二分图（鸽巢原理）
• Kn不是二分图（n>=3）
  K3: 其中一条边一定落在X或Y中

图的性质

• 证明：如果二分图G中存在回路，则它们都是 由偶数条边组成的。
  设C是二分图G的任一条回路，不妨设v0X 是C的始点，由于G是二分图，所以沿回路C必须经 过偶数条边才能达到某结点viX，因而只有经过偶 数条边才能回到v0

• 证明：设G是简单图，当m>(n-1)(n-2)/2时，G 是连通图。
  证明： 设 是非连通图，则它至少含有 2 个连通分支。设分别是 , ，其中
  , , ,
  。
  由于 是简单图，因此
  , 。

  所以
  
  与已知条件 矛盾，故 是连通图。

• n个结点的连通图的边数一定≥n-1

两点间距离,割点,割边

• 两点间距离：若u与v连通，则u与v之间最短道路长度为u与v的距离
• 割点：去掉该点（及关联边后），图的连通分支数上升
• 割边：去掉该边后，图的连通分支数上升

二、欧拉道路与回路

定义

无向连通图G=(V, E)中的一条经过所有边的简单回路(道路)称为G的欧拉回路(道路)
包含欧拉回路的图为欧拉图。

欧拉定理

定理2.3.1: 无向连通图G存在欧拉回路的充要条件是G中各结点的度都是偶数

必要性：若G中有欧拉回路C，则C过每条边一次且 仅一次．对任一结点v来说，如果C经过ei进入v，则 一定通过另一条边ej从v离开.因此结点v的度是偶数.

充分性：由于G是有穷图，因此可以断定，从G的任一结点v0出发一定存在G的一条简单回路C. 这是因为各结点的度都是偶数，所以这条简单道路不可能停留在v0以外的某个点，(有进有出)而不能再向前延伸以致构成回路C
如果E(G)=C, 则C就是欧拉回路，充分性得证。
否则在G中删去C的各边，得到G1=G-C。 G1可能是非连通图，但是每个结点的度保持为偶数。这时，G1中一定存在某个度非零的结点vi, 同时vi也是C 中的结点。否则C的结点与G1的结点之间无边相连， 与G是连通图矛盾。
同理，从vi出发，G1中vi所在连通分支内存在一条简单回路C1。(递归分析)
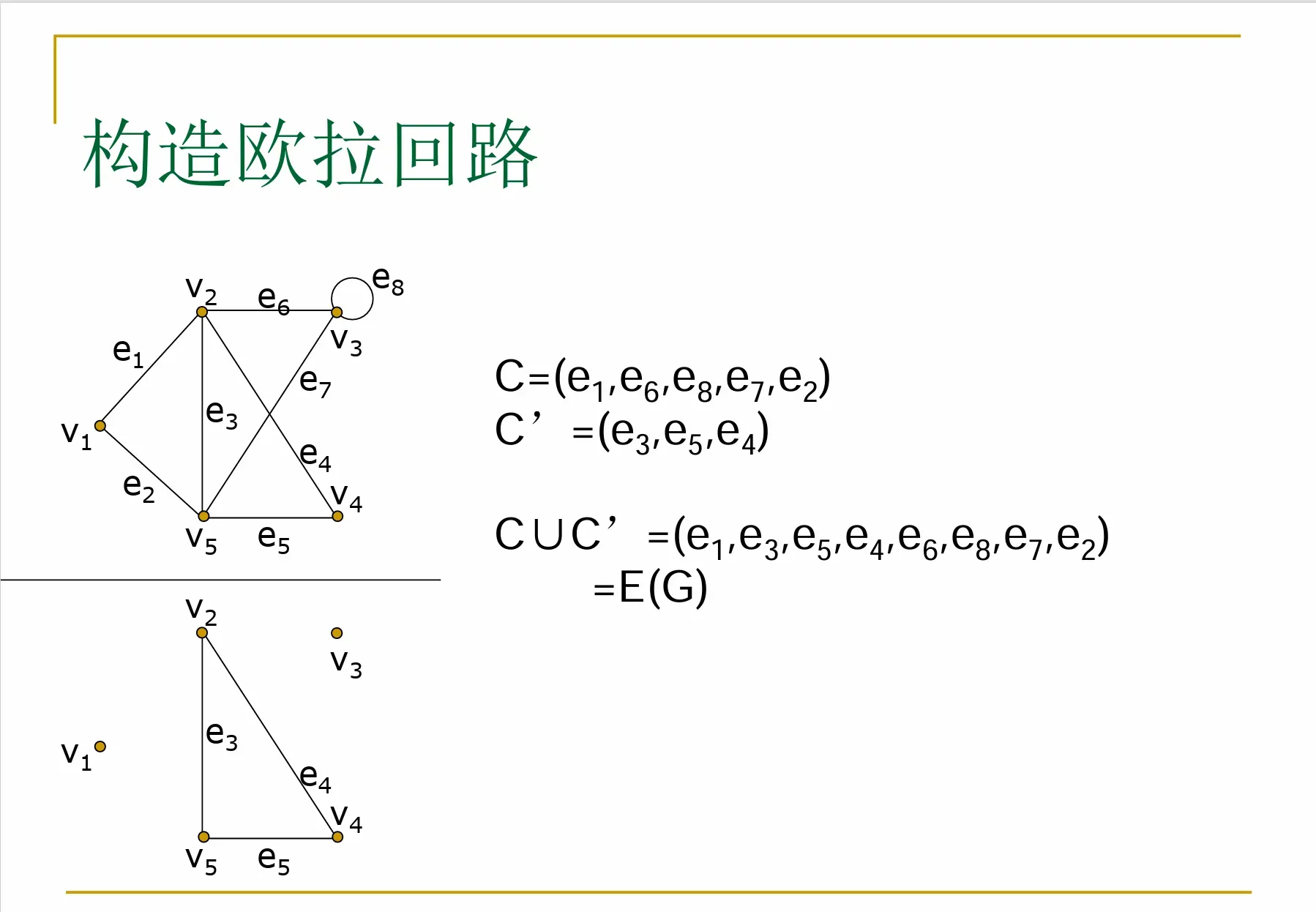
显然，C∪C1仍然是G的一条简单回路，但它包括的边数比C多。 继续以上构造方法，最终有简单回路C’= C∪C1∪…∪Ck ，它包含了G的全部边，即C’是G 的一条欧拉回路

也可以使用数学归纳法

构造欧拉回路:
方法同上证明: 先找一个小回路,再从小回路中能与外界联系的点出发继续找回路.

推论2.3.1: 若无向连通图G中只有2个度为奇的结点,则G存在欧拉道路.
证明：设vi和vj是两个度为奇数的结点. 作G’=G+(vi, vj), 则G’中各点的度都是偶数. 根据欧拉定理G’有欧拉回路, 它含边(vi, vj), 删去该边, 得到一条从vi到vj的简单道路, 它恰好经过了G的所有边, 亦即是一条欧拉道路

推论2.3.2: 若有向连通图G中各结点的正、负度相等, 则G 存在有向欧拉道路
证明类似于定理1

定理2.3.2: 设连通图G=(V,E)有k个度为奇数的结点， 那么E(G)可以划分成k/2条简单道路。

证明：由性质1.1.2，k是偶数。在这k个结点间增添 k/2条边，使每个结点都与其中一条边关联，得到 G’，那么G’中各结点的度都为偶数。 由定理1，G’包含一个欧拉回路C。而新添的 k/2条边在C上都不相邻。所以删去这些边后，我 们就得到由E(G)划分成的k/2条简单道路。

应用

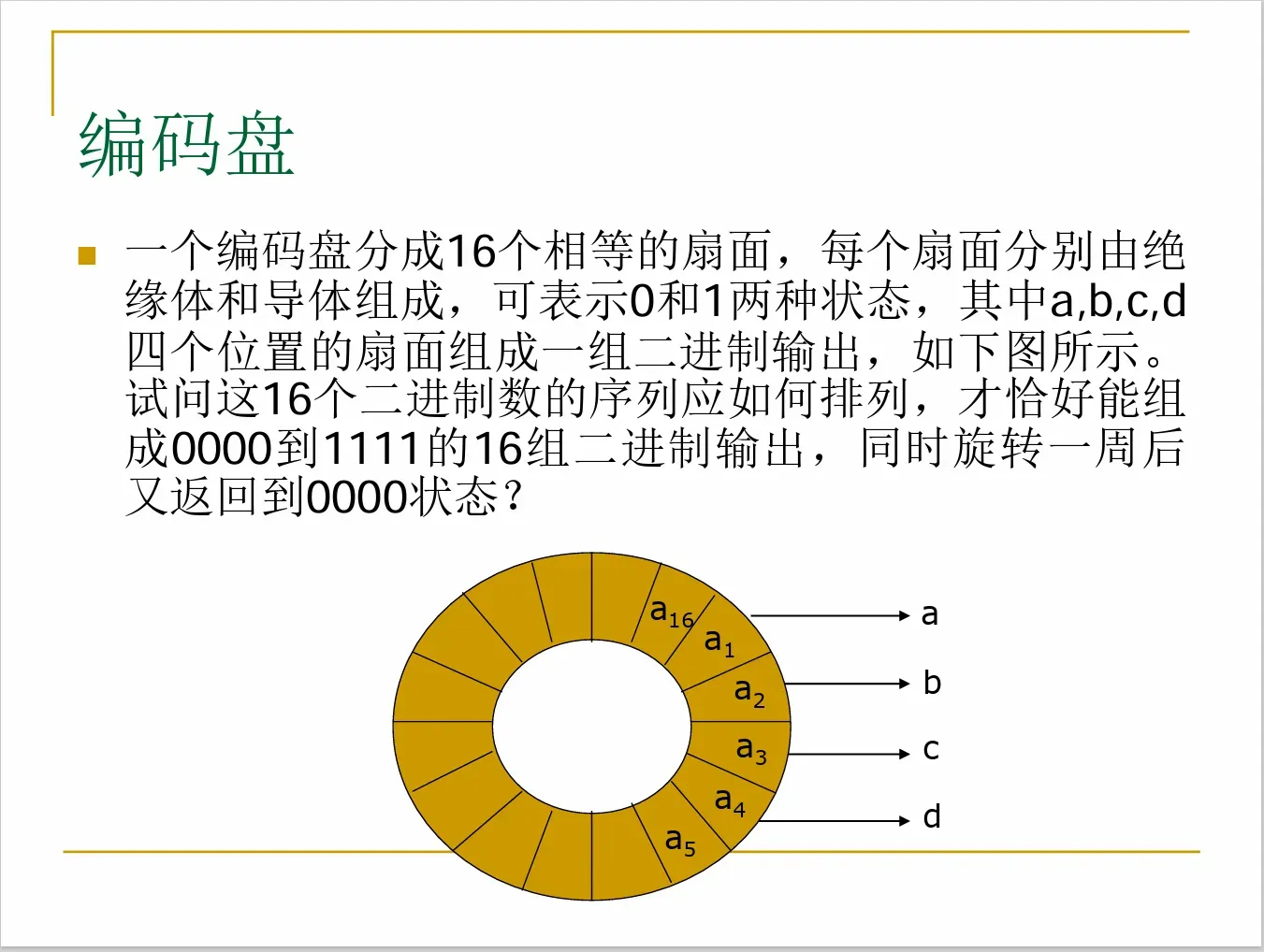
解答：如果从状态(=0或1)逆时针方向旋转一个扇面，那么新的输出是，其 中有三位数字不变。
因此可以用8个结点表示 从000到111这8个二进制数，这样从结点()可以到达结点()或()，其输出分别是()和()，这样可以得到下图。

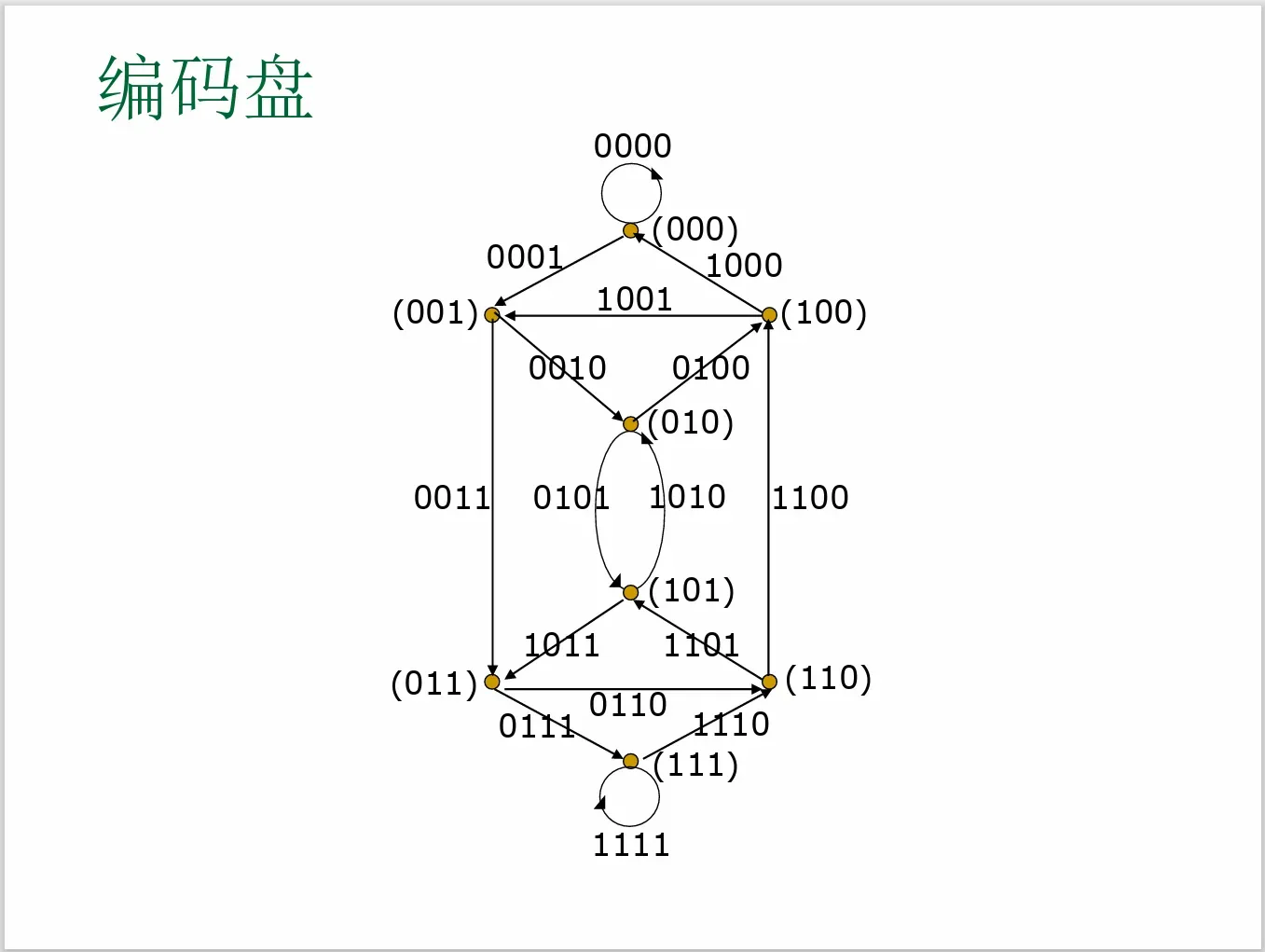
该图是有向连通图，共有16条边，且每结点的正、负度相等。有推论2.3.2，它存在有向欧拉回路。其中任一条都是原问题的解，比如(0000 1010 0110 1111)就是一个方案。 0000, 0001, 0010, 0101, 1010, 0100, 1001, 0011, 0110, 1101, 1011, 0111, 1111, 1110, 1100, 1000.

三、哈密顿道路与回路

定义(哈密顿图)

• 无向图的一条过全部结点的初级回路(道路)称为G 的哈密顿回路(道路),简记为H回路(道路)
• 哈密顿回路是初级回路，因此它与欧拉回路不同。当然在特殊情况下，G的哈密顿回路恰好也是其欧拉回路
• 判定H回路存在性问题一般是针对简单图的(删去重边与自环无影响)

回路-引理

引理*: 设P=(v1, v2, …, vl)是图G中一条极长的初级道路(即v1和vl的邻点都在P上)
而且d(v1)+d(vl)≥l，
则G中一定存在经过结点v1, v2, …, vl的初级回路。
Hint:

上面的推导过程: 对于与v1相连的每一个结点(vp), vl都不能与其前一个结点(vp-1)相邻,共有k个这样的结点,故l要减去k

哈密顿道路与回路-充分性定理1

定理2.4.1: 如果简单图G的任意两不相邻结点vi, vj之间恒有 d(vi)+d(vj)≥n-1 则G中存在哈密顿道路

证明:
先证G是连通图。若G非连通，则至少分为2个连通支H1, H2，其结点数分别为n1, n2。从中各任取 一个结点vi, vj，则 d(vi)≤n1-1， d(vj)≤n2-1。 故d(vi)+d(vj)<n-1. 矛盾

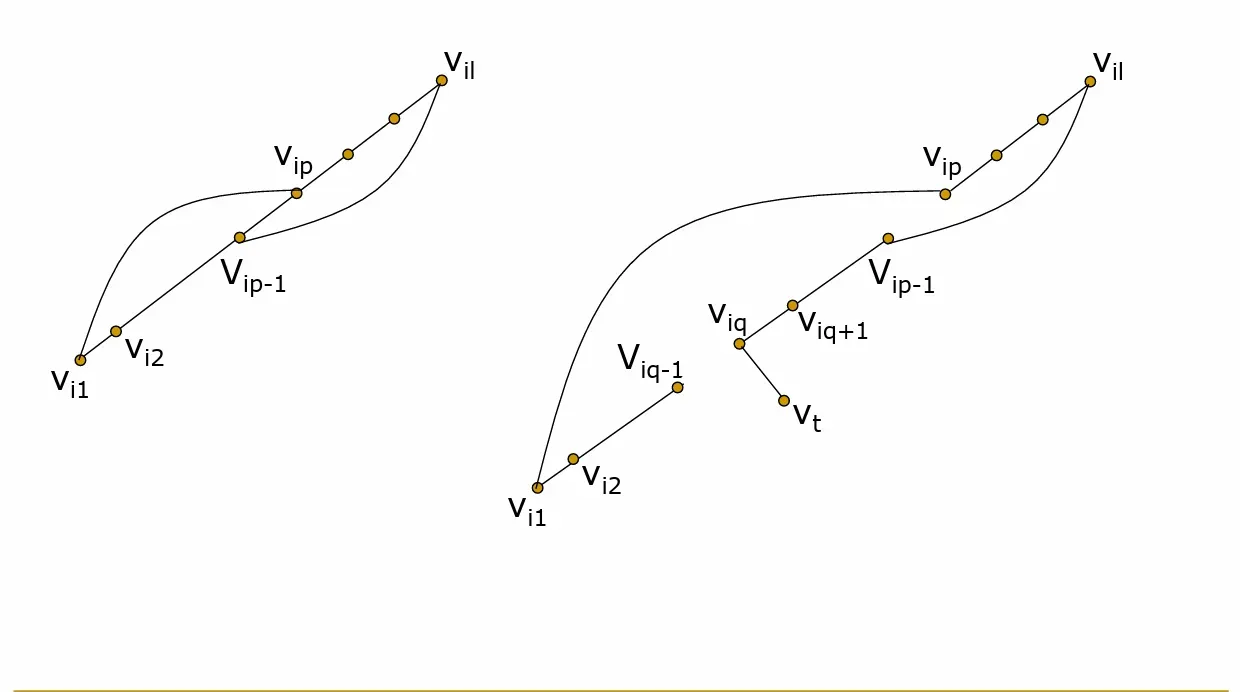
以下证G存在H道路。设P=(vi1, vi2, …, vil)是G中一 条极长的初级道路，即vi1和vil的邻点都在P上。此时，

1. 若l=n, P即为一条H道路
2. 若l<n,则可以证明G中一定存在经过结点vi1, vi2, …, vil的初级回路 C 。(引理*)

由于 连通，所以存在 之外的结点 与 中某点 相邻。删去 ，则 是 中一条比 更长的初级道路。以 的两个端点 和 继续扩充，可得到一条新的极长的初级道路。重复上述过程，因为 是有穷图，所以最终得到的初级道路一定包含了 的全部结点，即是 道路。

推论2.4.1（ORE）
若简单图G（n>=3）的任意两个不相临结点vi和vj之间恒有 d(vi)+d(vj)≥n 则G中存在哈密顿回路
证明：由定理2.4.1，G有H道路。设其两端点是v1和vn，若G不存在H回路，根据 回路-引理 证明，一定有：若d(v1)=k, 则d(vn)≤n-k-1， 那么d(v1)+d(vn)≤n-1

推论2.4.2（DIRAC）
若简单图Ｇ（n>=3）中每个结点的度都大于等于n/2，则G有H 回路
证明：由推论2.4.1可得。

闭合图

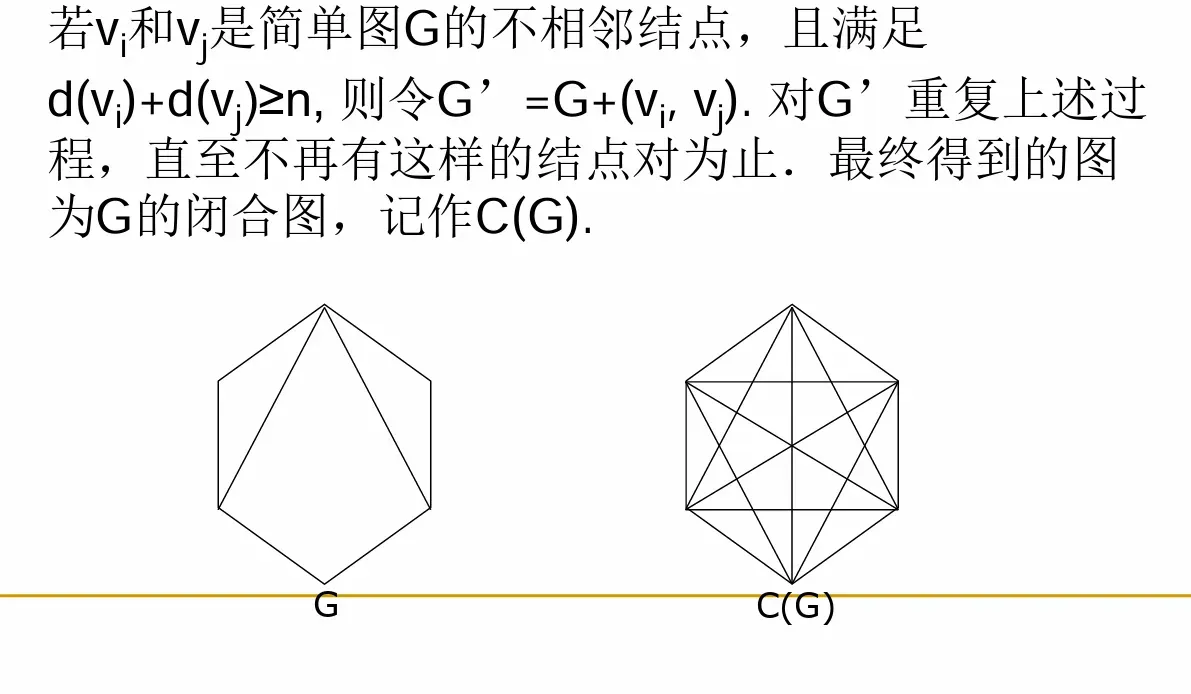
引理2.4.2 设G是简单图, vi,vj是不相邻结点，且满足 d(vi)+d(vj)≥n. 则G存在H回路的充要条件是G+(vi, vj) 有H回路
证明：必要性显然。现证充分性。假定G不存在H回路，则G+(vi,vj)的H回路一定经过边(vi,vj)，删去(vi,vj)， 即G中存在一条以vi,vj为端点的H道路，这时由 回路-引理 知必有 d(vi)+d(vj)<n (否则一定存在H回路), 而这与已知矛盾

哈密顿道路与回路-充分性定理2

定理2.4.2 简单图G存在哈密顿回路的 充要条件 是其闭合图存在哈密顿回路
闭合图的性质：任意两个不相邻结点，度之和>=n
证明：设C(G)=G∪L1, L1={e1, e2, …, et}, 由引理2.4.1和引理2.4.2， G有H回路G+e1有H回路… G∪L1有H回路.
由于C(G)是唯一的，故定理得证。

推论2.4.3 设G(n≥3)是简单图, 若C(G)是完全图Kn, G有H回路 说明:d(vi)+d(vj)=(n-1)+(n-1)=n+(n-2)

例子

举例：设n(≥3)个人中，任两个人合在一起都认识其余n-2个人。证明这n个人可以排成一队，使相邻者都互相认识。
证明：每个人用一个结点表示，相互认识则用边连接相应的结点，于 是得到简单图G。若G中有H道路，则问题得证。 由已知条件，对任意两点vi, vjV(G)，都有d(vi)+d(vj)≥n-2。此时，
(1)若vi和vj相识，即(vi,vj)E(G), 则d(vi)+d(vj)≥n
(2) 若vi和vj不相识，必存在vkV(G)，满足(vi,vk), (vj,vk) E(G)。否则， 设(vi,vk)E(G)，就出现vk, vj合在一起不认识vi，与已知矛盾。因此也有d(vi)+d(vj)≥n-1 综上由 充分性定理1，G中存在H道路

哈密顿道路与回路-必要性定理

必要性定理： 若G是H-图（此处特指H回路），则对于V的每个非空真子集S，均有W(G-S)≤|S|，其中 W(G-S) 是G-S中连通分支数。
证明：设C是G的H-回路，则对于V的每个非空真子集S均有W(C-S)≤|S|.(充分性定理2)
而C-S是G-S的生成子图，故W(G-S)≤W(C-S),因此W(G-S)≤|S|。