机器人运动学(Kinematics)是从几何角度描述和研究机器人的位置、速度和加速度随时间的变化规律的科学,它不涉及机器人本体的物理性质和加在其上的力。这里主要介绍机器人运动学的建模方法及逆运动学的求解方法。
3.0 引言
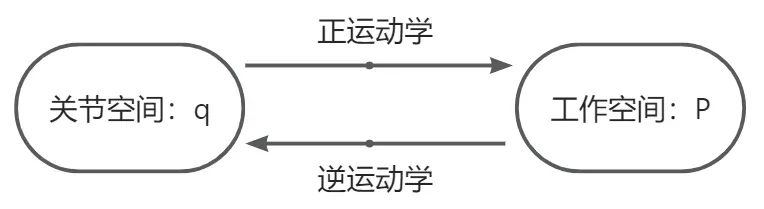
机器人运动学问题主要在机器人的工作空间与关节空间中讨论,包括正运动学(Forward Kinematics)和逆运动学(InverseKinematics)两部分内容。如图 3.1 所示,由机器人关节空间到机器人工作空间的映射称为正运动学,由机器人工作空间到机器人关节空间的映射称为逆运动学。正运动学也被称为运动学建模,而逆运动学也被称为运动学求逆或求逆解。
3.1 运动学建模
机器人运动学建模方法主要包括几何建模法、D-H建模法等。几何建模方法适用于结构简单的机器人,尤其是适合平面机器人。D-H建模方法具有较强的通用性,对于串联机器人、并联机器人都适用。本节重点介绍D-H建模方法。
1955年,Denavit和Hartenberg提出一种基于齐次变换矩阵的低副机构建模方法,该方法为每个连杆固连了一个坐标系,用 4×4 的变换矩阵描述相邻连杆的位姿关系,通过齐次变换建立运动学模型,被称为Denavit-Hartenberg参数模型,简称D-H模型,这种建模方法被称为D-H法。
目前,D-H建模方法主要有两种:标准 D-H 方法(Standard D-H method)和改进的 D-H 方法(Modified D-H method)。这两种方法主要区别在于坐标系建立的位置不同。Denavit和Hartenberg提出的方法被称为标准 D-H 方法。
https://blog.csdn.net/maple_2014/article/details/105612912
3.1.1 标准D-H方法
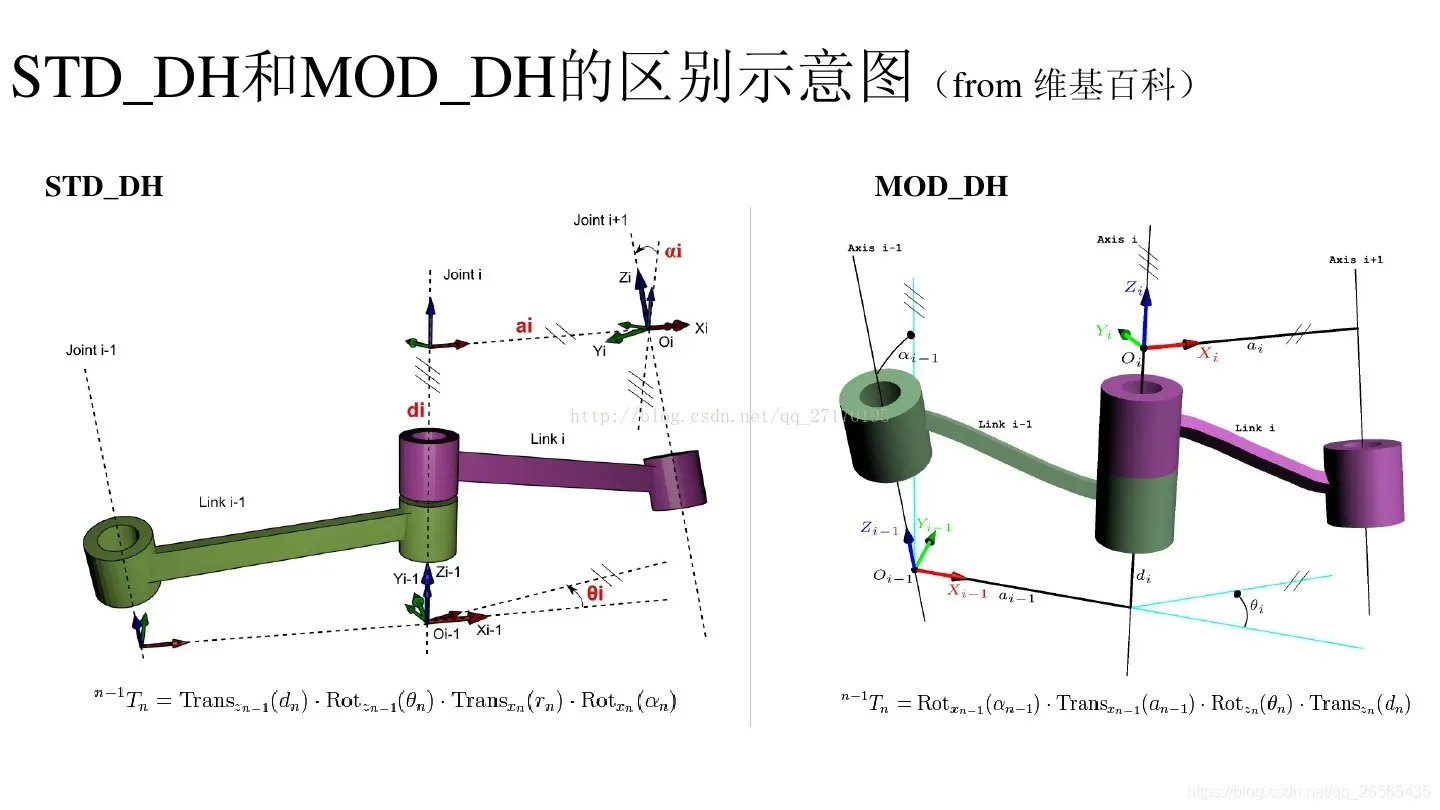
DH表示法一般步骤:首先为每个关节指定参考坐标系,然后确定如何实现任意两个相邻坐标系之间的变换,最后写出机器人的总变换矩阵。如图所示表示了三个顺序关节和两个连杆,每个关节都是可以转动和平移的。第一个关节指定为关节 i-1,第二个关节指定为关节 i,第三个关节指定为关节 i+1。在这些关节前后可能还有其他关节,连杆也是如此表示,连杆 i 位于关节 i 与关节 i+1 之间。
1、SDH建立每个关节参考坐标系步骤:
(1)所有关节,无一例外用 Z 轴表示。如果是关节是旋转的,Z 轴位于按右手定则选装的方向,如果关节是滑动的,Z 轴为沿实现运动的方向。在每一种情况下,关节 i 处的 Z 轴(以及该关节的本地参考坐标系)的下标为 i-1。
(2)坐标系 {i} 的原点设在关节 i 和关节 i+1 的轴线公垂线与关节 i+1 的轴线相交处。
(3)通常关节不一定平行或相交。因此,通常 Z 轴是斜线,但是总有一条距离最短的公垂线,它正交于任意两条斜线。通常在公垂线方向上定义 X 轴。所以如果 ai 表示 Zi−1与 Zi 之间的公垂线,则 Xi 的方向沿 ai。
(4)如果两个关节的 Z 轴平行,选取与前一关节的公垂线共线的一条公垂线,可简化模型;如果两个相邻关节的Z轴是相交的,那么它们之间没有公垂线,可选取两条 Z 轴的叉积方向作为 X 轴,可简化模型。
θ 角表示绕 Z 轴旋转角,d 表示在 Z 轴上两条相邻的公垂线之间的距离,a 表示每一条公垂线的长度,角 α 表示两个相邻的 Z 轴之间的角度。
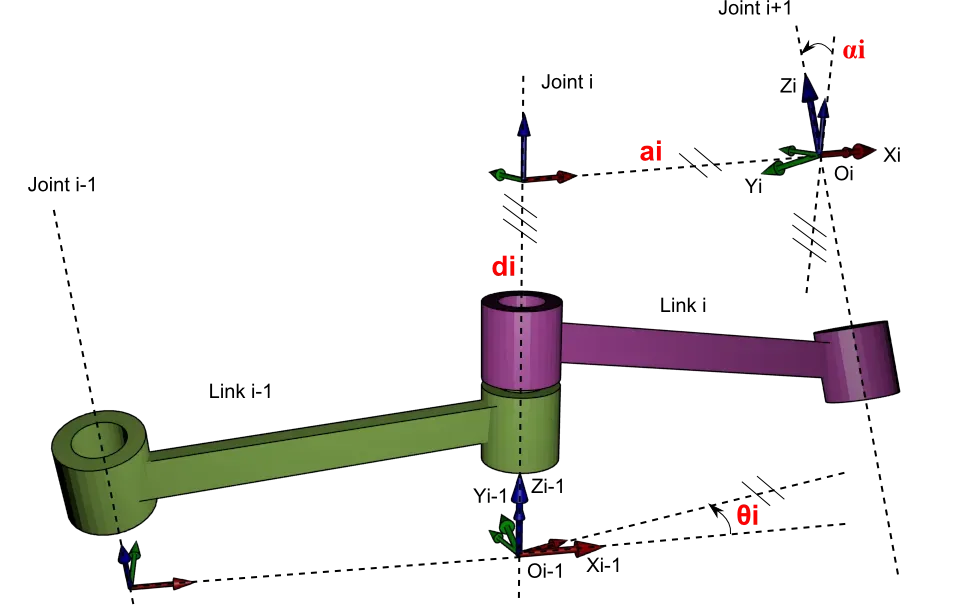
2、SDH建模步骤:
(1)绕 Zi−1轴旋转 θi,使 Xi−1和 Xi 同向;
(2)沿 Zi−1轴平移 di 距离,使 Xi−1 和 Xi 共线;
(3)沿 Xi 轴平移 ai 距离,使 Xi − 1 和 Xi 的原点重合;
(4)将 Zi − 1 轴绕 Xi 旋转 αi,使 Zi−1 轴与 Zi 轴共线。
通过右乘四个运动的四个矩阵就可以得到变换矩阵 :

3.1.2 改进D-H方法
1、MDH建立每个关节参考坐标系步骤:
(1)规定 Zi 轴沿关节轴 i 的指向。
(2)找出关节轴 i 和 i+1之间的公垂线或关节轴 i 和 i+1的交点,以关节轴 i 和 i+1的交点或公垂线与关节轴 i 的交点作为连杆坐标系{i}的原点。
(3)关节轴 i 和 i+1不相交时, Xi 轴与公垂线重合,指向从 i 到 i+1;如果关节轴 i 和 i+1相交,则规定 Xi 垂直于关节轴 i 和 i+1所在平面。
(4)按照右手定则确定 Yi 轴。
ai:沿 Xi 轴,从 Zi 移动到 Zi+1 的距离;
αi:绕 Xi 轴,从 Zi 旋转到 Zi+1 的角度;
di:沿 Zi 轴,从 Xi−1 移动到 Xi 的距离;
θi:沿 Zi 轴,从 Xi−1 旋转到 Xi 的角度;
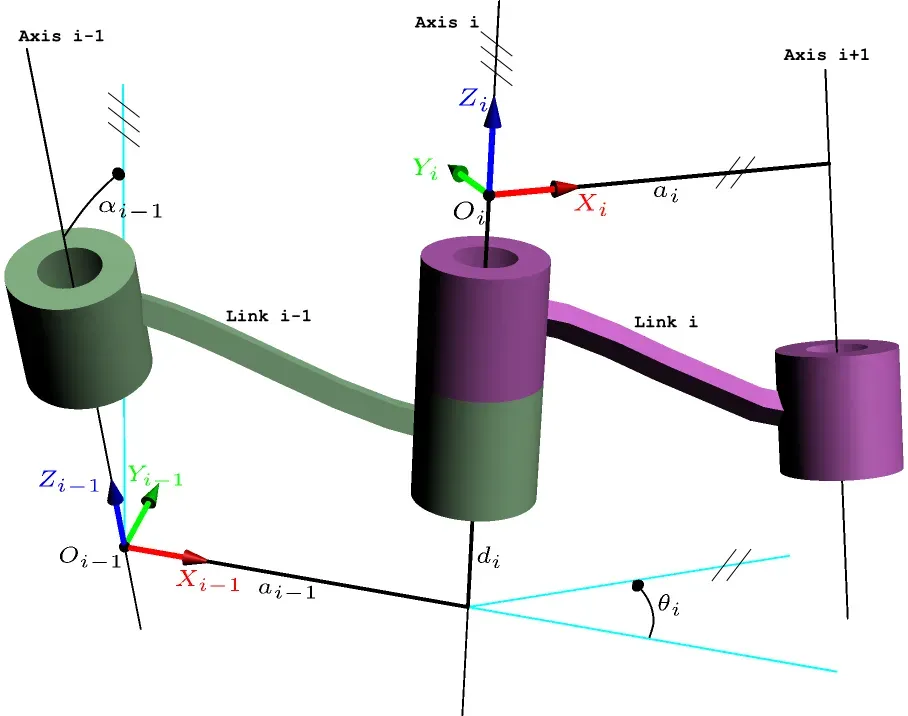
2、MDH建模步骤:
(1)将 Zi − 1 轴绕 Xi-1 旋转 αi-1,使 Zi−1 轴与 Zi 轴同向;
(2)沿 Xi-1 轴平移 ai-1 距离,使 Zi − 1 和 Zi 共线;
(3)绕 Zi 轴旋转 θi,使 Xi−1和 Xi 同向;
(4)沿 Zi 轴平移 di 距离,使 Xi−1 和 Xi 共线。
变换矩阵可以写成:
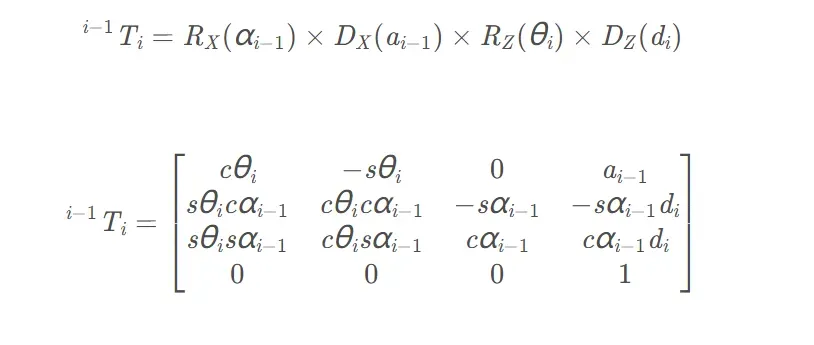
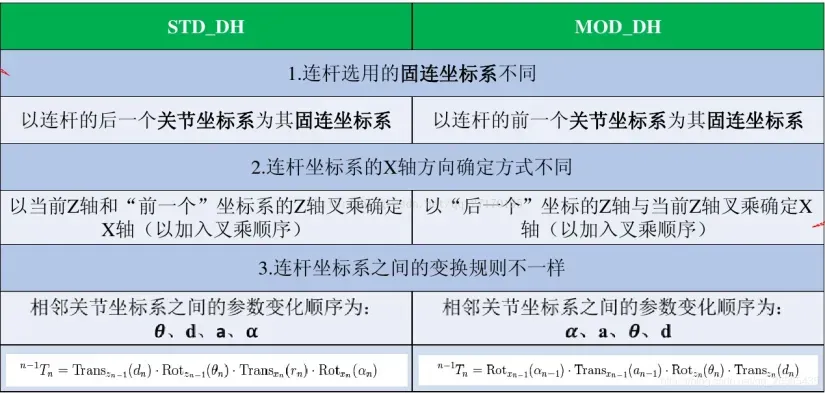
3.1.3 SDH与MDH比较
(1)固连坐标系不同
SDH方法关节 i 上固连的是 { i-1 } 坐标系,即坐标系建在连杆的输出端;MDH关节 i 上固连的是 { i } 坐标系,即坐标系建在连杆的输入端。
(2)坐标系变换顺序不同
SDH方法是 ZX 类变换:先绕着 { i-1 } 坐标系的的 Zi-1 轴旋转和平移,再绕着坐标系 { i } 的 Xi 轴进行旋转和平移;MDH方法是 XZ 类变换:先绕着 { i } 坐标系的的 Xi 轴旋转和平移,再绕着坐标系 { i } 的 Zi 轴进行旋转和平移。
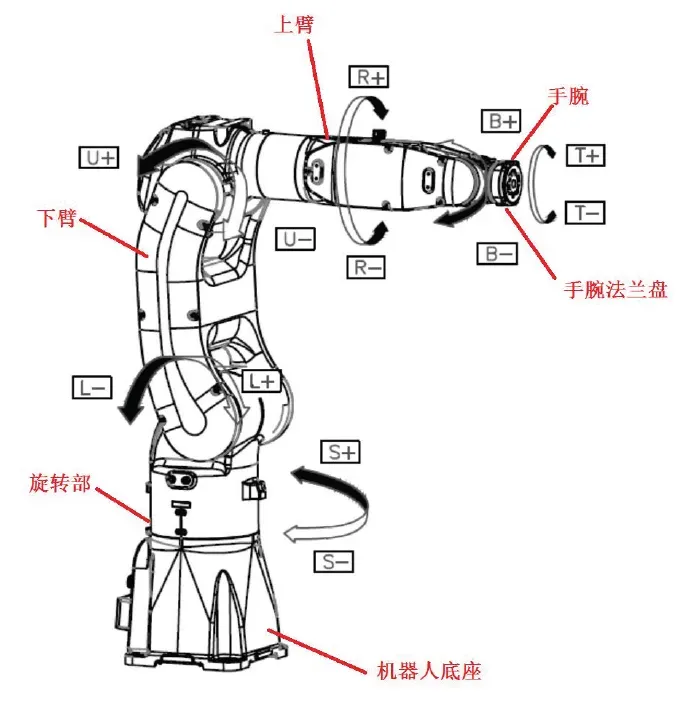
3.1.4 天机TR8 SDH建模

建立坐标系
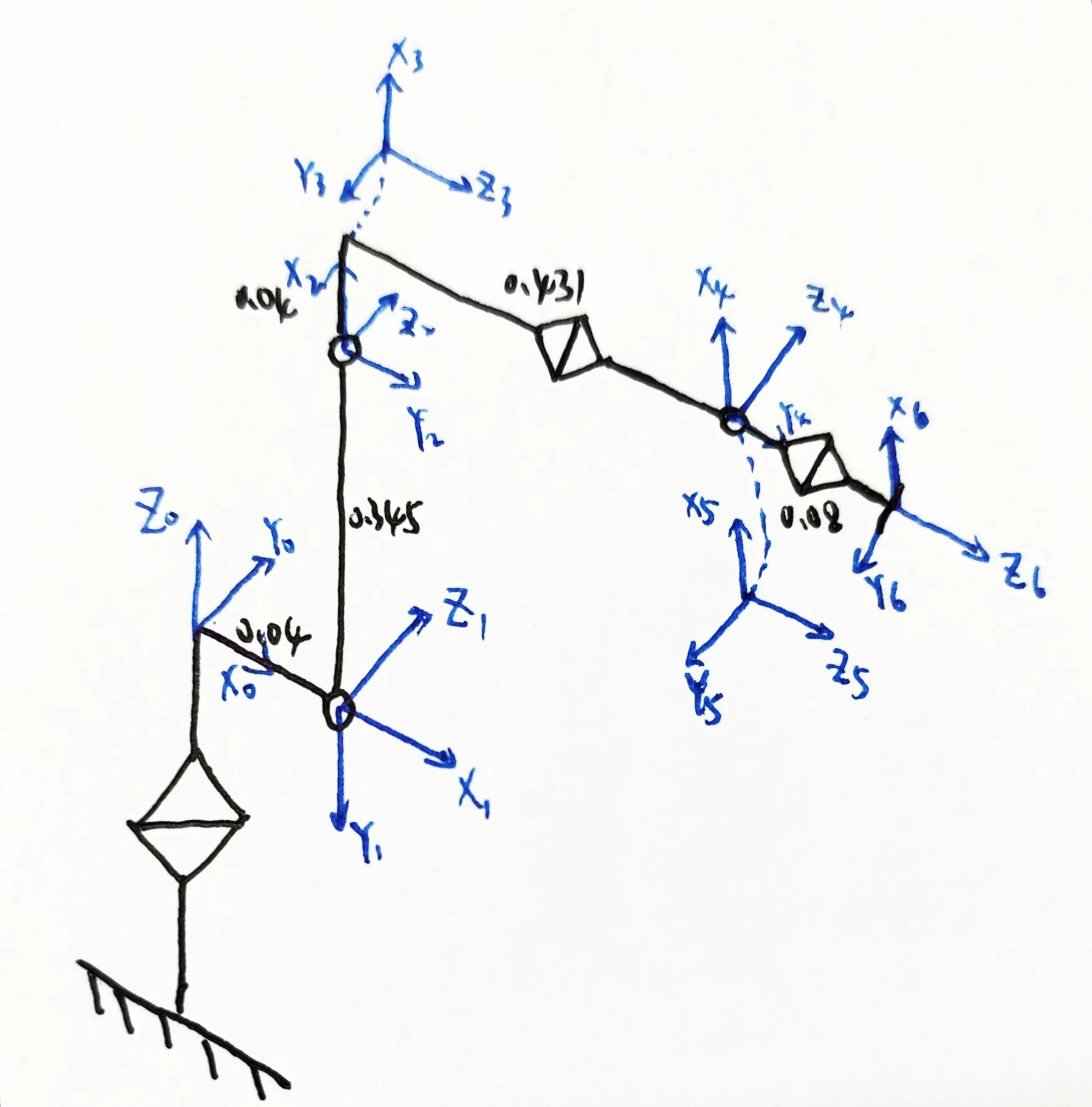
SDH表
| θ | d | a | α | |
|---|---|---|---|---|
| L1 | 0 | 0 | 0.04 | -pi/2 |
| L2 | -pi/2 | 0 | 0.345 | 0 |
| L3 | 0 | 0 | 0.04 | -pi/2 |
| L4 | 0 | 0.431 | 0 | pi/2 |
| L5 | 0 | 0 | 0 | -pi/2 |
| L6 | 0 | 0.08 | 0 | 0 |
关节范围:(单位/deg)
S:-170 ~ 170
L:-65 ~ 145
U:-70 ~ 190
R:-190 ~ 190
B:-135 ~ 135
T:-360 ~ 360
3.1.5 D-H法优势
空间任意两个坐标系的变换关系确实需要6个参数来表示,然而,在建立各个连杆的坐标系时,我们可以拟定一些规则,使得坐标系满足某些约束,从而只需4个参数则可以表示两个坐标系的变换关系。
若坐标轴 xi 与坐标轴 zi−1垂直相交(示例如下图),则只需4个参数(杆件长度 ai,杆件扭角 αi,关节距离 di,关节转角 θi )就可以表示两个坐标系的变换关系。下面的证明来于书籍:Robot Modeling and Control(First Edition),by Mark W. Spong, Seth Hutchinson, and M. Vidyasagar.
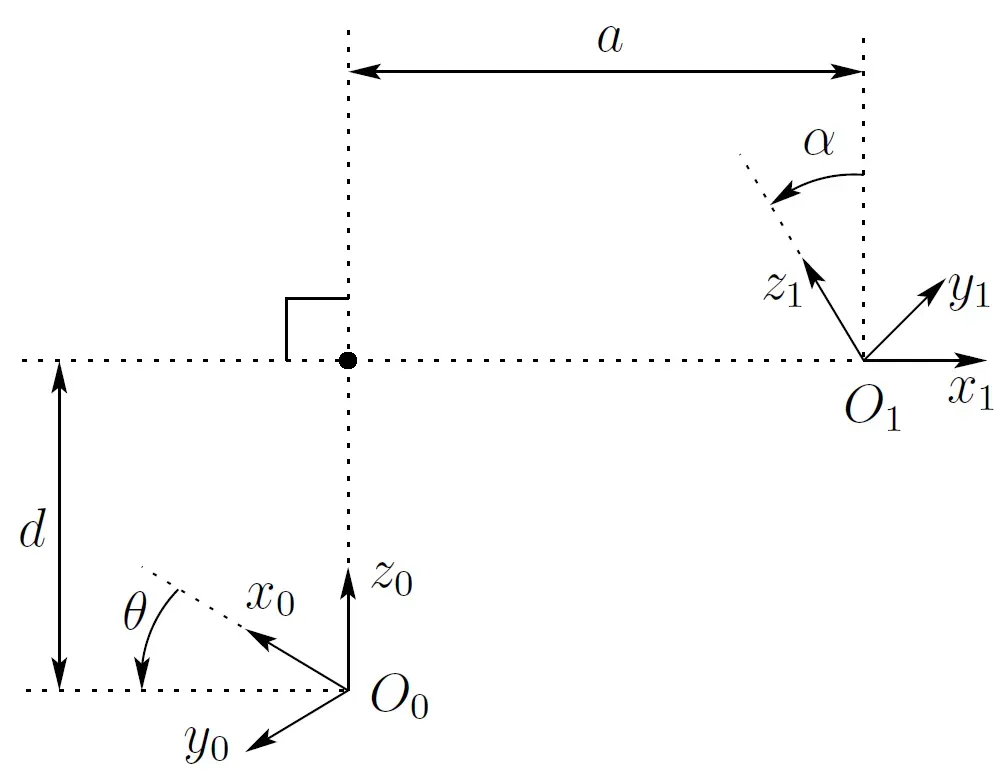
若坐标系与坐标系
垂直相交,则坐标系
到坐标系
的齐次变换矩阵为:
(1)式可以写成:
因为 x1 垂直于 z0,故有:
由于,只要证明存在唯一的杆件扭角 α ,关节转角 θ,使得:
因此,存在唯一的 θ , α 满足:
易得:
根据旋转矩阵的性质,可以推导得到:
可见,坐标系 到坐标系
的旋转变换关系用 θ , α 来表达就足够了。
若 x1与 z0 相交,坐标系 的原点在坐标系
下的坐标(或平移向量)为:
综上,坐标系到坐标系
的齐次变换关系用杆件长度 a,杆件扭角 α,关节距离 d,关节转角 θ 这4个参数就够了。
3.2 正逆运动学
正运动学指,从机器人的关节空间描述计算笛卡尔空间描述的机器人末端执行器的位置和姿态,该问题通常是一个几何问题,给定一组关节角度,计算末端坐标系相对于基坐标系的位置和姿态。
逆运动学指,从笛卡尔空间描述下的机器人末端执行器位置和姿态反算出机器人关节空间应该达到的关节角度组合,是实现机器人控制的一个基本问题。通常因为正运动学方程是非线性的,因此逆运动学问题较为困难,很难得到封闭解,甚至无解。
https://blog.csdn.net/hanmingjunv5/article/details/106555302
https://zhuanlan.zhihu.com/p/450749372
3.2.1 机器人正运动学
机器人正运动学就是给定机器人各关节位置,计算机器人连杆上任意点的位姿。
此过程为:建立机器人运动学方程。
位姿矩阵
机器人位置和姿态可以由一个方阵描述:
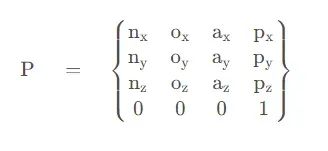
正运动学求解
为 k 关节坐标系在 i 关节坐标系下的描述。
对于确定的机器人结构,每个关节在上一关节的描述是确定的,因此正运动学直接计算即可。
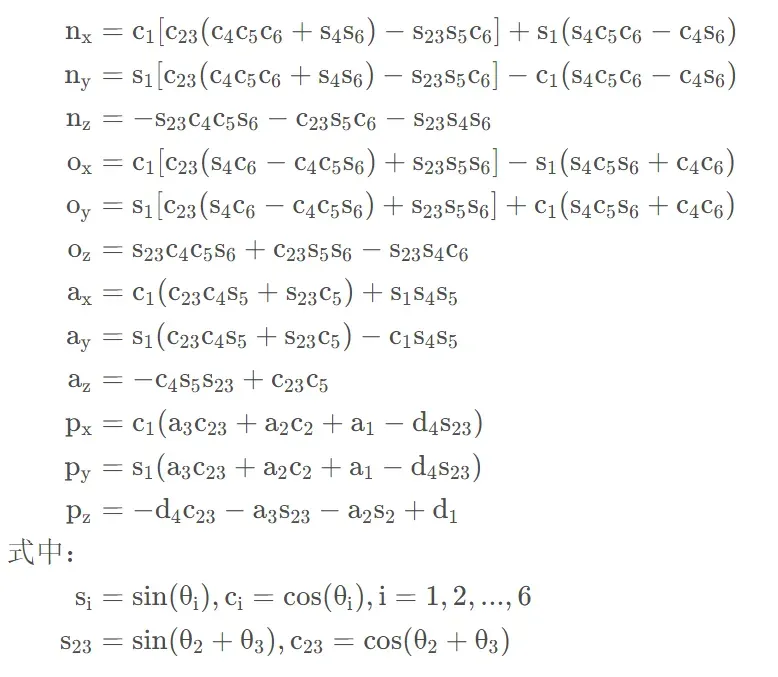
3.2.2 机器人逆运动学
逆运动学求解通常有两大类方法:解析解、数值解。
一、解析解(Analytical Solution)
解析解通常被称为封闭解(Closed Form Solution),就是可以将求解的关节变量表示成解析表达式的形式,是精确解。
特点:运算速度快(达到us级),通用性差,可以分为代数法与几何法进行求解。
串联机械臂有逆运动学解析解的充分条件是满足Pieper准则。即如果机器人满足两个充分条件中的一个,就会得到封闭解,这两个条件是:
- (1)三个相邻关节轴线交于一点;
- (2)三个相邻关节轴线相互平行。
现在的大多数商品化机器人都满足封闭解的两个充分条件之一。如PUMA和STANFORD机器人满足第一条件,而ASEA和MINIMOVER机器人满足第二条件。
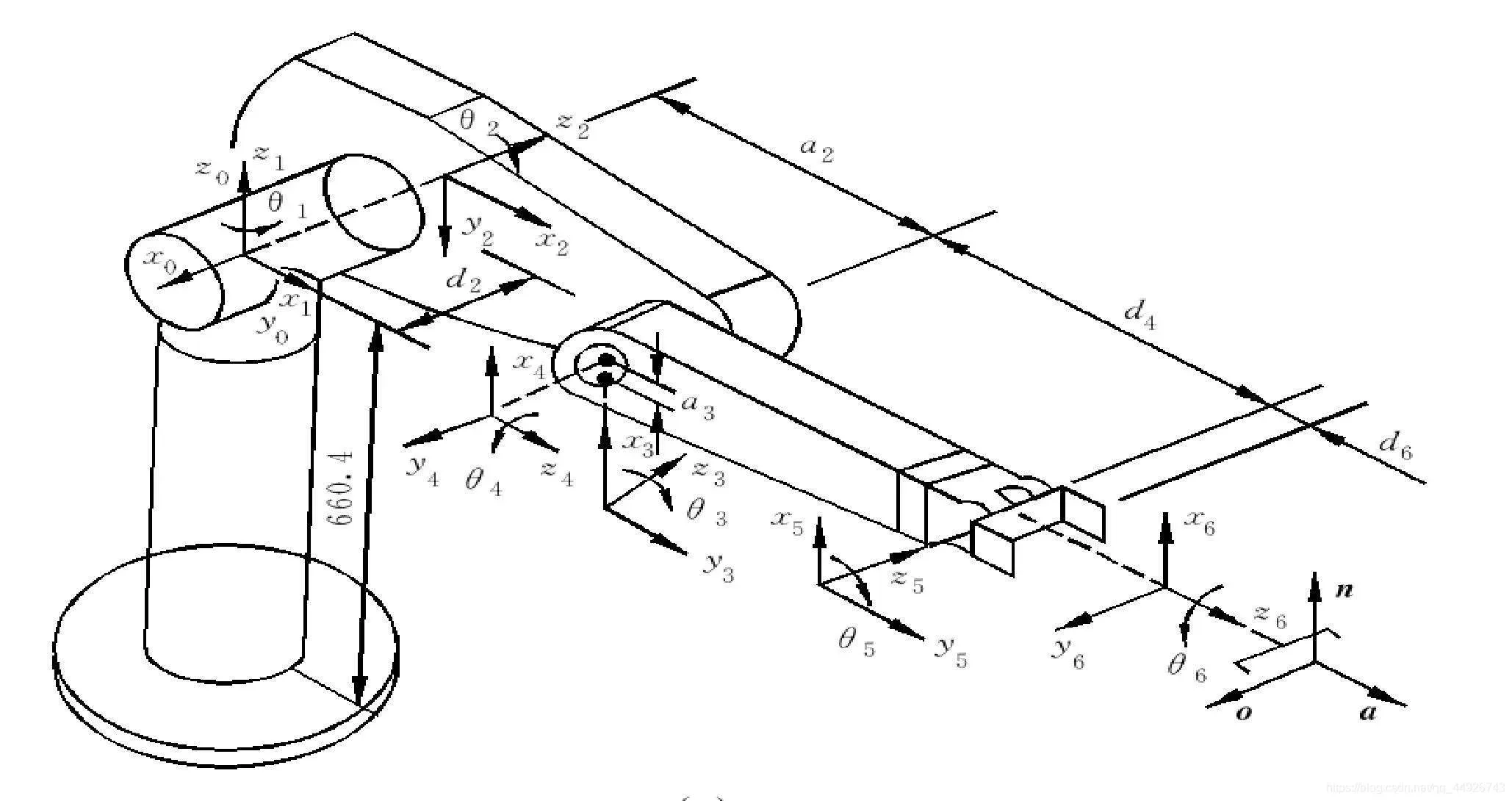
以PUMA560机器人为例,它的最后3个关节轴相交于一点,该点通常被称为腕点。
版权声明:本文为博主作者:压力士原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/weixin_43724057/article/details/129739113
