目的:在传统的向量叉乘计算中,常常遇到叉乘。定义为向量。其这个向量方向满足右手定则。它的模大小,一般被忽略。因此推测一下。
向量叉乘定义:
外积(英语:Cross product)又称向量积(英语:Vector product),是对三维空间中的两个向量的二元运算,用符号:表示。可以定义为:
假设两个向量外积,它的方向为
。其方向由右手定则决定。模长等于这两个向量边的平行四边形的面积。
它的定义也可以写成:
其中为两个向量的夹角
;
分别为两个向量
的模长。
为垂直于
所在平面的法向量,且它满足右手定则。如下图:
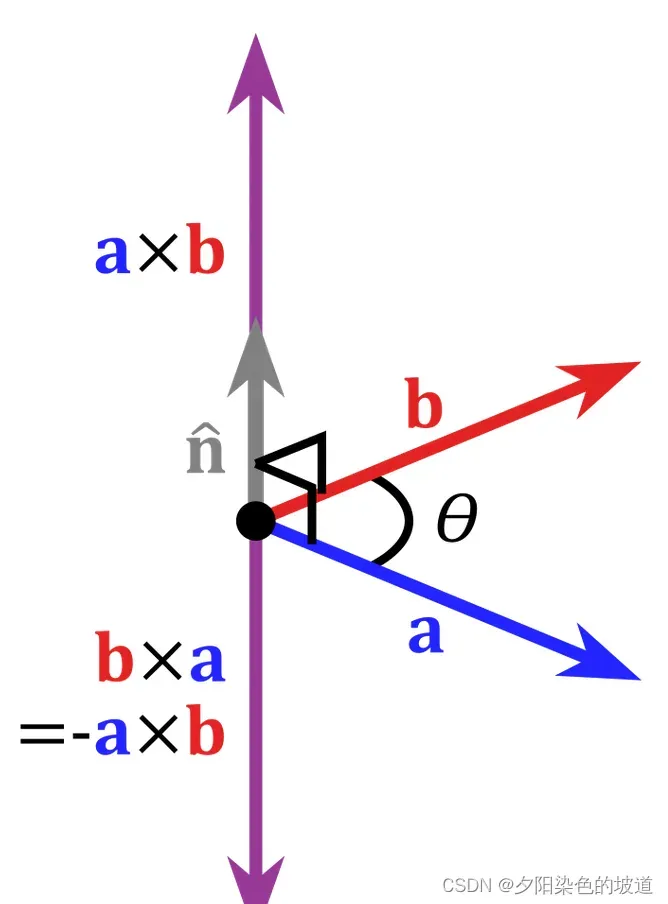
因为基向量两两垂直,且为单位向量。
表示都为
的向量。所以得到:
将代入公式
得到如下:
公式的,在日常用行列式计算表达。使用
的矩阵余子式计算方式。它和代数计算方式相等。
因为它为基向量,在欧式几何中,它的表达为:
因此代入到
得到:
上面是基于基向量的表达,它和上面的公式对应,因此可以得到:
在一些应用,经常向量的表示转化为矩阵的运算。因此(13)公式可以表示矩阵和向量的乘法。
两个向量的叉乘仅仅在三维空间有定义。在二维空间没有定义。
下面介绍向量的行列式和向量组成的平行四边形面积的关系。
假设为二维向量。这样易于解释。因此画图如下:
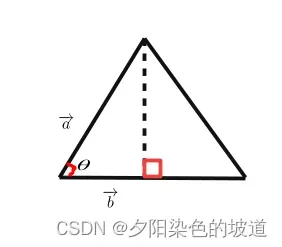
转化一下表达,因为不好计算,需要计算
。
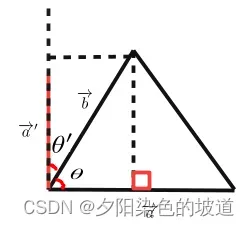
其中.且
,容易得到公式简化,简化上述等式为:
因为是通过
旋转90度得到的,如下图。
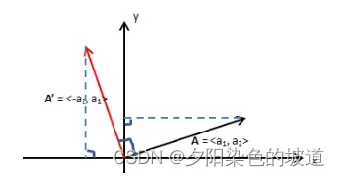
因此假设 得到
因此得到公式:
可以看到行列式是面积的表达。
文章出处登录后可见!
已经登录?立即刷新
