1.引言 

       在之前使用长短期记忆网络构建电力负荷预测模型的基础上，将自注意力机制 (Self-Attention)融入到负荷预测模型中。具体内容是是在LSTM层后面接Self-Attention层，在加入Self-Attention后，可以将负荷数据通过加权求和的方式进行处理，对负荷特征添加注意力权重，来突出负荷的影响因数。结果表明，通过自注意力机制，可以更好的挖掘电力负荷数据的特征以及变化规律信息，提高预测模型的性能。

        环境：python3.8，tensorflow2.5.

2.原理

2.1.自注意力机制

        自注意力机制网上很多推导，这里就不再赘述，需要的可以看博客，这个博客讲的很好。

2.2 模型结构

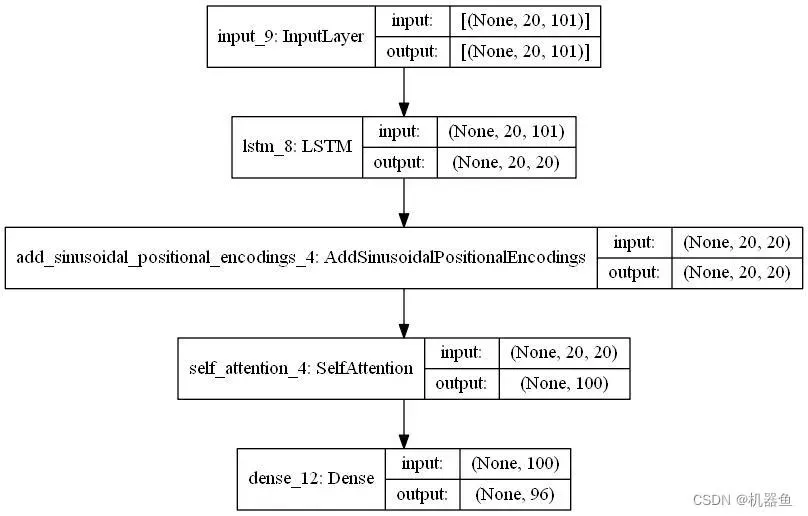
主要包含输入层，LSTM层，位置编码层，自注意力机制层，以及输出层。

3. 实战

3.1 数据结构

        采用2016电工杯负荷预测数据，每15分钟采样一次，一天共96个负荷值与5个气象数据（温度湿度降雨量啥的）。我们采用滚动建模预测，就是利用1到n天的所有值为输入，第n+1天的96个负荷值为输出；然后2到n+1天的所有值为输入，第n+2天的96个负荷值为输出，这样进行滚动序列建模。这个n就是时间步，程序里面设置的是20，所以上面的输入层你看到是Nonex20x101,输出是Nonex96。

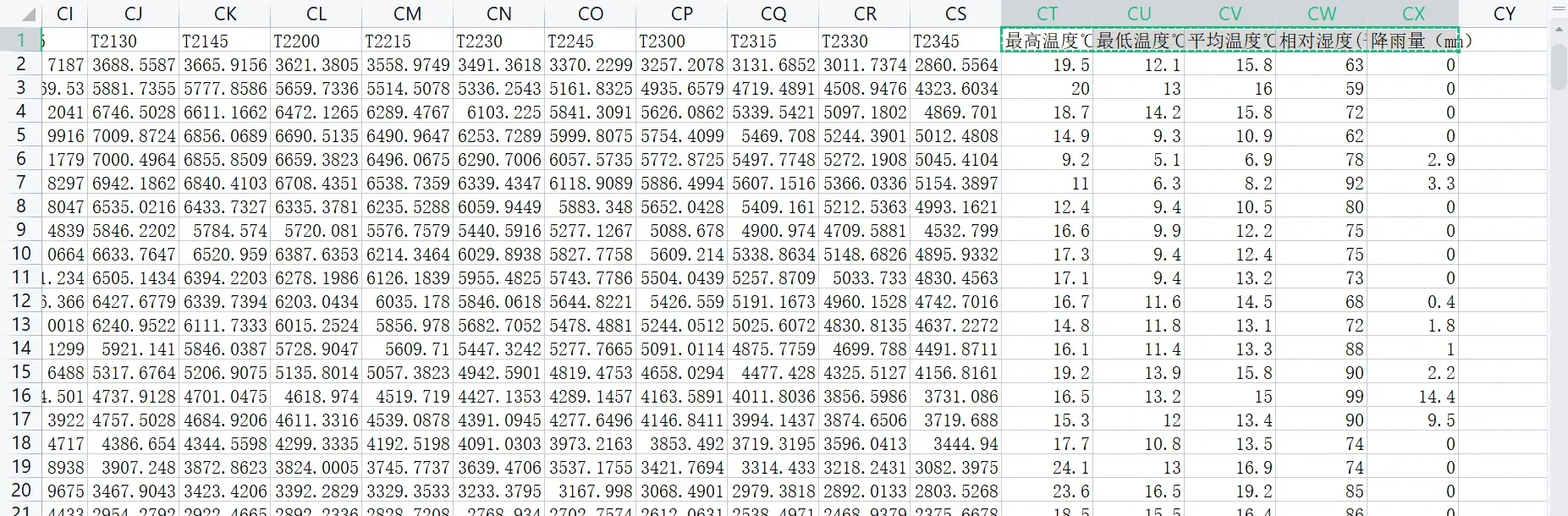
3.2 建模预测

# coding: utf-8
from sklearn.preprocessing import StandardScaler,MinMaxScaler
from sklearn.metrics import r2_score
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input,Dense,LSTM
import tensorflow as tf
from Layers import SelfAttention,AddSinusoidalPositionalEncodings
os.environ["PATH"] += os.pathsep + 'C:/Program Files (x86)/Graphviz2.38/bin/'
from tensorflow.keras.utils import plot_model

# In[]定义一些需要的函数

def build_model(seq,fea,out):
    input_ = Input(shape=(seq,fea))
    x=LSTM(20, return_sequences=True)(input_)    
    pos = AddSinusoidalPositionalEncodings()(x)
    att = SelfAttention(100,100,return_sequence=False, dropout=.0)(pos)
    
    out = Dense(out, activation=None)(att)
    model = Model(inputs=input_, outputs=out)
    return model


def split_data(data, n):
    in_ = []
    out_ = []    
    N = data.shape[0] - n
    for i in range(N):
        in_.append(data[i:i + n,:])
        out_.append(data[i + n,:96])
    in_ = np.array(in_).reshape(len(in_), -1)
    out_ = np.array(out_).reshape(len(out_), -1)
    return in_, out_
def result(real,pred,name):
    # ss_X = MinMaxScaler(feature_range=(-1, 1))
    # real = ss_X.fit_transform(real).reshape(-1,)
    # pred = ss_X.transform(pred).reshape(-1,)
    real=real.reshape(-1,)
    pred=pred.reshape(-1,)
    # mape
    test_mape = np.mean(np.abs((pred - real) / real))
    # rmse
    test_rmse = np.sqrt(np.mean(np.square(pred - real)))
    # mae
    test_mae = np.mean(np.abs(pred - real))
    # R2
    test_r2 = r2_score(real, pred)

    print(name,'的mape:%.4f,rmse:%.4f,mae：%.4f,R2:%.4f'%(test_mape ,test_rmse, test_mae, test_r2))

# In[]
df=pd.read_csv('数据集/data196.csv').fillna(0).iloc[:,1:]
data=df.values
time_steps=20
in_,out_=split_data(data,time_steps)

n=range(in_.shape[0])
#m=int(0.8*in_.shape[0])#前80%训练 后20%测试
m=-2#最后两天测试
train_data = in_[n[0:m],]
test_data = in_[n[m:],]
train_label = out_[n[0:m],]
test_label = out_[n[m:],]

# 归一化
ss_X = StandardScaler().fit(train_data)
ss_Y = StandardScaler().fit(train_label)
# ss_X = MinMaxScaler(feature_range=(0, 1)).fit(train_data)
# ss_Y = MinMaxScaler(feature_range=(0, 1)).fit(train_label)
train_data = ss_X.transform(train_data).reshape(train_data.shape[0], time_steps, -1)
train_label = ss_Y.transform(train_label)

test_data = ss_X.transform(test_data).reshape(test_data.shape[0], time_steps, -1)
test_label = ss_Y.transform(test_label)
# In[]
model=build_model(train_data.shape[-2],train_data.shape[-1],train_label.shape[-1])
#查看网络结构
model.summary()
plot_model(model, show_shapes=True, to_file='result/lstmsa_model.jpg')

train_again=True  #为 False 的时候就直接加载训练好的模型进行测试
#训练模型
if train_again:
    #编译模型
    model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.001), loss='mse')
    #训练模型
    history=model.fit(train_data,train_label,batch_size=64,epochs=100,
                      verbose=1,validation_data=(test_data,test_label))
    # In[8]
    model.save_weights('result/lstmsa_model.h5')
    loss = history.history['loss']
    val_loss = history.history['val_loss']
    plt.plot( loss, label='Train Loss')
    plt.plot( val_loss, label='Test Loss')
    plt.title('Train and Val Loss')
    plt.legend()
    plt.savefig('result/lstmsa_model_loss.jpg')
    plt.show()
else:#加载模型
    model.load_weights('result/lstmsa_model.h5')

# In[]
test_pred = model.predict(test_data)

# 对测试集的预测结果进行反归一化
test_label1 = ss_Y.inverse_transform(test_label)
test_pred1 = ss_Y.inverse_transform(test_pred)
# In[]计算各种指标
result(test_label1,test_pred1,'LSTM-SA')
np.savez('result/lstmsa1.npz',real=test_label1,pred=test_pred1)

test_label=test_label1.reshape(-1,)
test_pred=test_pred1.reshape(-1,)
# plot test_set result
plt.figure()
plt.plot(test_label, c='r', label='real')
plt.plot(test_pred, c='b', label='pred')
plt.legend()
plt.xlabel('样本点')
plt.ylabel('功率')
plt.title('测试集')
plt.show()

 3.2 结果对比

        将其与RNN、LSTM进行对比，结果如下

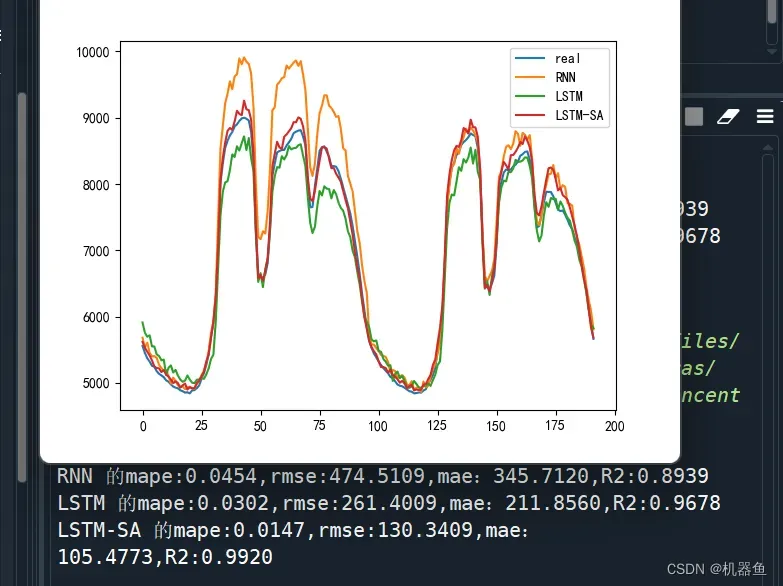
测试集取的是最后两天的，从结果上看，显然提出的方法效果最好 

4.代码

        详细代码见评论区。