多层感知机（MLP）、全连接神经网络（FCNN）、前馈神经网络（FNN）、深度神经网络（DNN）与BP算法详解

本篇文章涉及较多的基础知识，并且篇幅较长，是其它的更为复杂的神经网络的基础，需要重点掌握该神经网络的结构特征、网络的训练方法等内容。

一：概念辨析

兔兔在命名标题时，使用了这么多的名称，主要是因为这些名称，从本质上来讲几乎都是指相同的神经网络，只是其侧重点有所不同，其中也有较为细微的差别。

首先，对于多层感知机（Multilayer perceptron）,其结构基础是单层感知机，或者是逻辑回归。对于这两种基础的结构，它们的特点是：只有两层神经元，输入层有多个输入（神经元），输出一般只有一个神经元，结构如下所示：

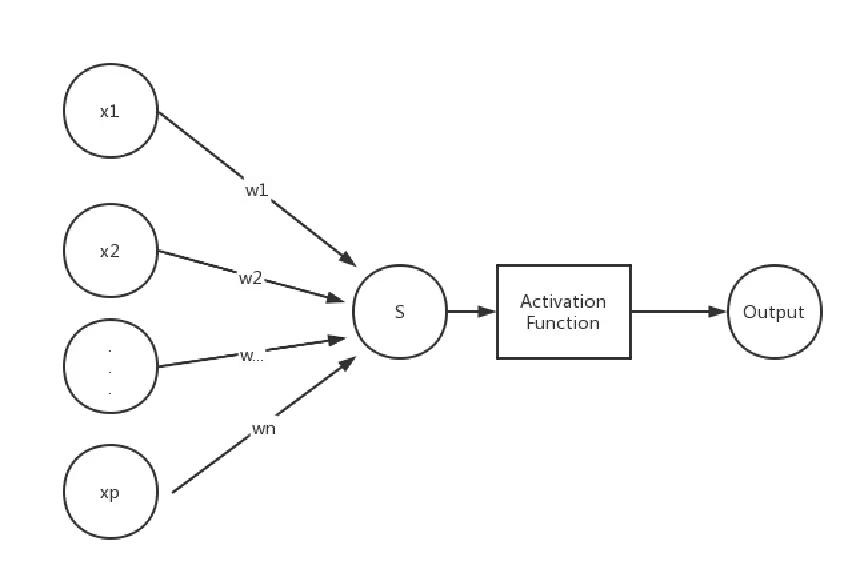
如果在这个结构中多加入若干层这样的神经元，类似于多个单层感知机的叠加，即是多层感知机，只不过此时的激活函数也不一定是sign函数，往往是sigmoid等激活函数，而且输入也不一定仅仅是一个神经元，根据具体问题的需要也可以是多个神经元，结构图如下所示：

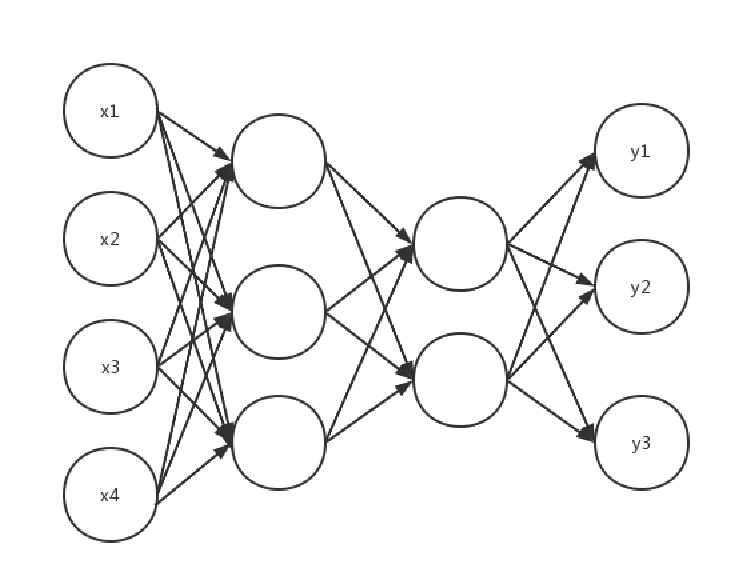
上图所示即是一个含有四层神经元的一个神经网络，最左边的四个神经元为输入层，最右边三个神经元为输出层，中间两层为隐藏层。

其次，如果我们从这个神经网络的结构特征来考虑，我们发现，从第二层神经元开始，每一层的每个神经元都与前一层的所有神经元相连接；从第一层开始，除最后一层，每一层神经元都有后一层所有神经元之间相连接，并且层内神经元互不相连。所以，从这个神经网络是结构来看，可以称作是全连接神经网络（Fully connected neural network,FCNN）。

从数据流动方向来看，从第二层神经元开始，每一层神经元都可以接收前一层的输出，并输出给下一层，即整体上数据从左到右逐层传递，信号从输入层到输出层单向传播。所以，从信号（数据）传递方向上看，可以称作是前馈神经网络（Feedforward neural network,FNN）。

对于一个神经网络，其模型的关键不止是其结构，更重要的是如何训练这个神经网络，如何利用数据集进行 “学习”。对于这样的神经网络，最常用的训练方法就是反向传播（Back propagation,BP）算法。所以利用这样BP算法来训练这样的神经网络，就可以称作BP神经网络。更准确的说，BP神经网络一定是MLP,FCNN,FNN，但如果该神经网络不用BP算法进行训练，就不能叫做BP神经网络了。

对于这种神经网络，虽然名称不同，但是本质上却是相同的。就好比对于一个堤坝，可以只考虑堤坝这个结构，根据堤坝来命名；同时也可以看水流的方向，根据水流特点来命名；堤坝水闸具有调控水流大小的特点，也可以根据这个特点来命名，但实质是类似相同的东西。

至于深度神经网络（Deep neural network,DNN），其名称是与浅层神经网络（Shallow neural network,SNN）相对应。例如逻辑回归、单层感知机等，其结构只有两层神经元，都是浅层神经网络（对于支持向量机（SVM），也有人认为是浅层神经网络一种，但SVM本质上是机器学习的一种方法，不属于神经网络范畴）。而对于前面讲到的神经网络，如果隐藏层比较少，如2~3层，则也可以认为是浅层神经网络的一种。那么如果增加更多的隐藏层，是否就是DNN呢? 对于一般的FCNN/FNN/MLP，它们往往使用sigmoid作为激活函数，但是这个激活函数有一个缺点：随着神经元层数的增加，会出现梯度消失，为了避免梯度消失，可以减少神经元层数，也就是某种意义上的SNN。如果增加更多的神经元的层数，同时避免梯度消失，可以采用ReLU等激活函数，此时在某种意义上来说可以是深度神经网络。DNN与SNN 一样，本质上是一类神经网络的总称，FCNN中隐藏层很多时可以是DNN，卷积神经网络（CNN）、循环神经网络（RNN）等，如果层数很多，也是DNN的一种。

在一般的文章中，或许是考虑与单层感知机等模型的差别，习惯上把含有较少的隐藏层的FCNN也称作是DNN神经网络。在本篇文章中，由于使用了BP算法，并且为了叙述方便，将该神经网络统一称作BP神经网络。

二：BP神经网络生物学原理

即然命名为神经网络，肯定是与生物体的神经网络有着相似之处，就像遗传算法、免疫算法、蚁群算法等，其算法流程往往与其对应的生物学特性有着较为一致的方面，但同时也并不是完全相同。所以学习时重点还是实际的算法流程，其中的生物学原理可以作为兴趣稍微了解一下。

在神经系统中，各个神经元之间相互连接，在神经元之间，神经信号从前一个神经元的轴突传递到下一个神经元胞体的树突端；对于神经元自身，从树突端接收信号后传递到轴突端，再通过轴突传递信号给下一个个神经元树突。并且各个神经元可以向下个神经元传递信号，下一个神经元接受来自前面的所有神经元的信号后可能会兴奋，也可能是抑制，取决于前面神经元的信号是抑制还是兴奋，也取决与这个神经细胞自身。

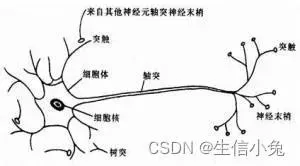
由此可见，神经信号的传递是有方向的并且是单向的，一个神经细胞只能接收前面细胞的信号并可能向下传递信号。在BP神经网络中也是如此，信号（数）只能从前传递到后，每个节点（神经元）接收前面的信号，由激活函数处理后决定是否向下传递信号。

三：BP神经网络结构与信号（数据）传递

（1）训练数据集的特征

对于一个BP神经网络，我们的目的是通过已有的数据对该神经网络进行训练，从而能够利用这个神经网络实现分类、预测、识别等功能。以一个简单的分类问题为例：对于一个含有n组数据、p个指标的数据集X，每组数据都对应一个类y，整个样本一共有m类。我们用一个BP神经网络，对数据集X进行数据挖掘（或者说是神经网络的学习）。训练完成后，对一个未知类别的一组数据，可以将该数据输入到整个神经网络并从输出得到该组数据属于哪一类。由于输入层，每个神经元对应一组数据某一个指标的数值，所以输入层需要p个神经元；对于输出层，每一个神经元都代表一个类，输出时哪一个神经元激活（输出结果为1），则该组数据属于哪一类，所以输出层需要m个神经元。至于中间需要多少隐藏层，每层有多少神经元，是可以在合理的条件下任意选取的。

（2）BP神经网络结构

BP神经网络的结构兔兔在前面已经展示了，兔兔在这里还是以这个含有四层神经元的神经网络为例。把这个神经网络具体展开，实际的结构如下图所示：

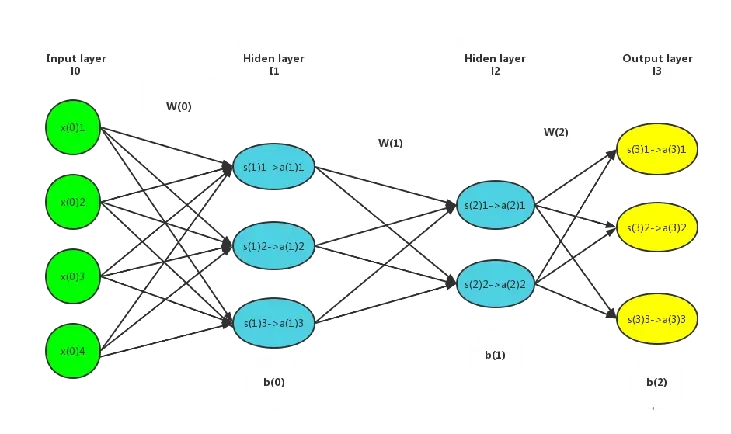
在这个网络中，数据的指标个数为4，我们令输入的一组数据为 $\textbf{x}=(x_{1},x_{2},x_{3},x_{4})^{T}$ ，由于输入数据x在输入层，即这里的第1层 $l_{0}$ ，所以也可以表示成 $\textbf{x}^{(0)}=(x_{1}^{(0)},x_{2}^{(0)},x_{3}^{(0)},x_{4}^{(0)})^{T}$ ;下一层 $l_{1}$ 中的各个s值可以由向量 $\mathbf{s}^{(1)}=(s_{1}^{(1)},s_{2}^{(1)},s^{(1)}_{3})^{T}$ 整体表示，相应的各个a由 $\textbf{a}^{(1)}=(a_{1}^{(1)}, a_{2}^{(1)}, a_{3}^{(1)})^{T}$ 表示（对于向量中的元素，右上角代表该数所在神经元层数，右下角代表在该层神经元是第几个神经元）。最终输出得到的 $\mathbf{a}^{(3)}$ , 也就是 $\textbf{y}=(y_{1},y_{2},y_{3})^{T}$ 。

我们先以 $l_{0}$ 层第1个神经元与 $l_{1}$ 层所有神经元之间信号传递为例。对于 $l_{1}$ 层的第一个神经元，其与上一层 $l_{0}$ 所有神经元相连，设该神经元与这4个神经元的连接权值分别为 $w^{(0)}_{11},w^{(0)}_{12},w^{(0)}_{13},w^{(0)}_{14}$ ，则

$s^{(1)}_{1}=w^{(0)}_{11}x^{(0)}_{1}+w^{(0)}_{12}x^{(0)}_{2}+w^{(0)}_{13}x^{(0)}_{3}+w^{(0)}_{14}x^{(0)}_{4}+b^{(0)}_{1}$

即某一层中某一神经元的数值s等于与它连接的前一层所有神经元输出值对于乘以相应的权值再求和，加上偏置b。所以可以总结为：

$s^{(l+1)}_{m}=w_{m1}^{(l)}a^{(l)}_{1}+w_{m2}^{(l)}a_{2}^{(l)}+...+w_{mn}a^{(l)}_{n}+b^{(l)}_{m}$

其中l表示第l层，m表示第l+1层第m个神经元，n表示第l层神经元总数， $w_{mn}^{(l)}$ 表示第l+1层第m个神经元与第l层第n个神经元之间的权值， $b_{m}^{(l)}$ 表示l+1层第m个神经元的偏置。

为了运算与表示的简便，我们可以把层与层之间的权值写成矩阵形式，即权值矩阵W；偏置写成向量形式，即偏置向量b。权值矩阵的维数为m×n,m为两层神经元右侧的神经元个数，n为左侧神经元个数，矩阵的i行j列表示右侧层第i个神经元与左侧层第j个神经元之间的权值。则上式可以简化成：

$\mathbf{s}^{(l+1)}_{m\times 1}=W^{(l)}_{m\times n}.\mathbf{a}^{(l)}_{n \times 1}+\textbf{b}^{(l)}_{m \times 1}$

除了输入层，在之后的每一层神经元中，都需要将s变成a在输出，这个过程实际上就是激活函数的作用。我们令激活函数为f(x),则：

$a^{(l)}_{n}=f(s^{(l)}_{n})$

如果用向量来整体表示，则：

$\mathbf{a}^{(l)}=f(\textbf{s}^{(l)})=(f(s^{(l)}_{1}),f(s^{(l)}_{2}),...,f(s^{(l)}_{n}))^{T}$

（3）总结

根据上面的内容，我们已经初步了解BP神经网络的结构，知道其中的信号传递过程，兔兔在这里总结如下：

（1）对 $l_{1}$ 层：

$\mathbf{s}^{(1)}=W^{(0)}.\mathbf{x}^{(0)}+\textbf{b}^{(0)} \\\textbf{a}^{(1)}=f(\mathbf{s}^{(1)})$

（2）对 $l_{2}$ 层：

$\mathbf{s}^{(2)}=W^{(1)}.\mathbf{a}^{(1)}+\textbf{b}^{(1)} \\\textbf{a}^{(2)}=f(\mathbf{s}^{(2)})$

（3）按（1）（2）规律逐层传递。最后一层输出的a即为输出结果。

（4）算法实现

import numpy as np
class BP:
   def __init__(self,x,y,node=[4,3,2,3]):
      self.x=x #训练数据
      self.y=y #数据对应的类别
      self.w=[np.random.normal(size=(node[i+1],node[i])) for i in range(len(node)-1)]
      self.b=[np.random.normal(size=(node[i+1],1)) for i in range(len(node)-1)]

初始时权值W与偏置b先进行随机初始，把各层的权值矩阵和偏置向量都保存在一个列表中，便于之后的数据处理。

信号前向传递过程中需要用到激活函数，所以在BP类中可以再定义一个激活函数，兔兔在这里选取常用的sigmoid 函数。

class BP:
    def __init__(self,x,y,node=[4,3,2,3]):
        '''略'''
    def sigmoid(self,x):
        '''激活函数'''
        return 1/(1+np.exp(-x))
    def forward(self,x):
        '''信号前向传递'''
        s0=np.dot(self.w[0],x)+self.b[0]
        a0=self.sigmoid(s0)
        for i in range(1,self.n-1):
            s=np.dot(self.w[i],a0)+self.b[i]
            a=self.sigmoid(s)
            a0=a
        return a0

这里暂时还没有用到数据集，其中x,y可以随便数凑位置，然后测试一下正向传递的效果。

if __name__=='__main__':
   bp=BP(x=1,y=1)
   output=bp.forward(x=np.mat([1,2]).T)
   print(output)

需要注意的是，输入x需要是一个列向量，并且输入向量的维数要与输入层神经元个数相同，否则无法计算，程序报错。

注意：在整个算法实现过程中，需要时刻注意数据类型，注意每次运算过程中是列表、数、矩阵还是序列，在矩阵、向量乘积中注意结果的维度。例如：在矩阵或向量乘积过程中，我们通过数学计算可能会得到一个数，但是np中矩阵乘积得到的是1×1的矩阵，而不是数，如果不及时转换一下数据类型，程序很可能会报错，导致无法进行。

四：BP算法

BP算法是BP神经网络的核心，是神经网络能够学习的根源所在，也是BP神经网络中最难的部分。与之前的逻辑回归等内容相似，我们需要构造损失函数，然后求损失函数对各个参数的偏导数，利用梯度下降等方法不断调整参数，进而达到训练神经网络的目的。只不过在这里，神经元的层数增加，信号是逐层传递的，各个权值、偏置等参数众多，需要涉及部分矩阵求导等知识，所以更为复杂。

（1）损失函数的构造与数据集训练方法

在神经网络中，损失函数的种类是非常多的，兔兔在这里使用均方差损失函数。所谓的损失函数，即表示神经网络的预测值与实际值的差别，差别越大，损失函数数值越大，神经网络预测效果越差。我们通过损失函数，不断调整权值与偏置参数，使得损失函数越来越小，进而能够实现更加准确的预测。

设训练样本X有n组数据，指标为p,则损失函数可以为：

$Loss=\sum_{i=1}^{n}\frac{1}{2}||a_{i}-y_{i}||^{2}$

但是在实际的训练过程中，数据中样本个数往往很多，利用所有的数据来计算，会使得计算速度慢，效果不好。通常情况下可以使用随机梯度下降(SGD)的方法，把数据集n个样本分成样本个数为m的各个batch，每次更新参数使用batch，并且所有数据随机选取。

def BP:
    def __init__(x,y,node=[4,3,2,3],batchlength=20)
        '''略'''
        self.batchlength=batchlength
    def batches(self):
        '''把数据集分成长度为batchlength的各个batch'''
        data=list(zip(self.x,self.y))
        np.random.shuffle(data)
        batches=[data[i:i+self.batchlength]for i in range(0,len(data),self.batchlength)]
        return batches

（2）损失函数对W与b的偏导数求解

兔兔在这里还是以前面的神经网络图（各层神经元数：4，3，2，3）为例。开始时需要画神经网络简图以及正向传递的式子。

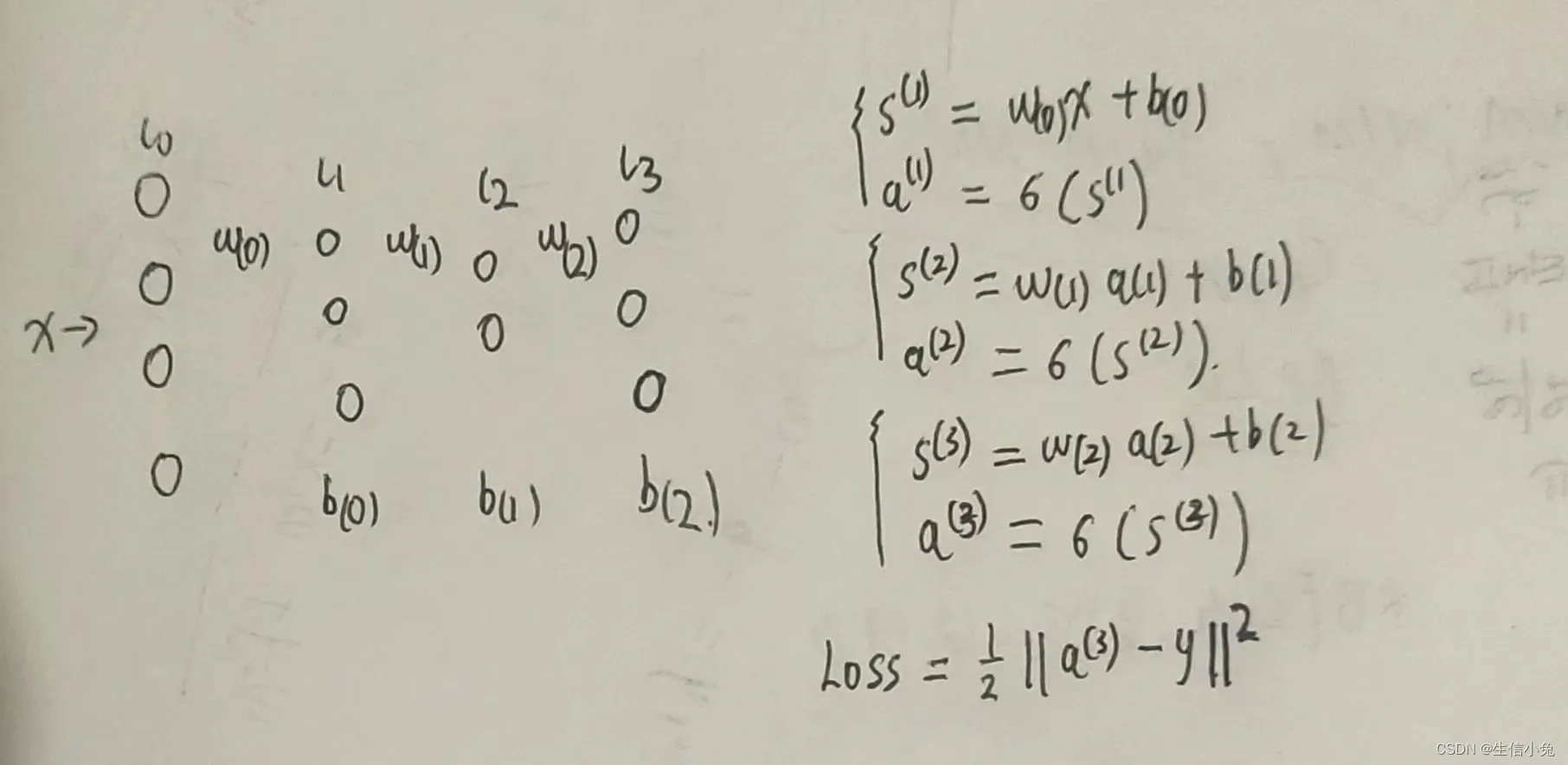
对于求解损失函数对权值与偏置的导数，理论上是可以把损失函数详细展开，求对权值矩阵或偏置向量中各个数的偏导，但是这样计算量过于庞大，且无规律可循。我们所期望的是能够求得Loss对矩阵W与向量b的导数，这样整体计算更加简洁，计算更加简便。

在正向传播过程中，信号是从左向右逐层传递的，我们能够依次得到各层的s与a;在反向传播过程中，则是根据损失函数，从右向左逐层传递，依次得到Loss对W与b的偏导。反向传播过程依赖于链式求导原理。例如，我们求Loss对 $W^{(2)}$ 的导数，即Loss对 $\mathbf{a}^{(3)}$ 的偏导乘 $\mathbf{a}^{(3)}$ 对 $\mathbf{s}^{(3)}$ 的偏导乘 $\textbf{s}^{(3)}$ 对 $W^{(2)}$ 的偏导。只不过这里矩阵的求导与普通的函数求导不同，各个偏导不是简单的依次相乘。

我们在求偏导的过程中，是始终有一条主线的——Loss对各层的s从右向左依次求偏导。在这个神经网络中，我们可以先求 $\frac{\partial Loss}{\partial \textbf{s}^{(3)}}$ ,这样就可以比较方便的求出 $\frac{\partial Loss}{\partial W^{(2)}}, \frac{\partial Loss}{\partial \mathbf{b}^{(2)}}$ ；之后 $\frac{\partial Loss}{\partial \textbf{s}^{(2)}}=\frac{\partial Loss}{\partial \mathbf{s}^{(3)}}.\frac{\partial \textbf{s}^{(3)}}{\partial \mathbf{s}^{(2)}}$ ，由这个式子可以很方便地求出 $\frac{\partial Loss}{W^{(1)}},\frac{\partial Loss}{\partial \textup{b}^{(1)}}$ ；最后 $\frac{\partial Loss}{\partial \textbf{s}^{(1)}}=\frac{\partial Loss}{\partial\textbf{ s}^{(3)}}.\frac{\partial \textbf{s}^{(3)}}{\partial \textbf{s}^{(2)}}.\frac{\partial \textbf{s}^{(2)}}{\partial \textbf{s}^{(1)}}$ ，求出W(0)与b(0)的梯度。

遵循上述规律，我们的问题关键是找到依次求Loss对s的偏导的规律，以及s对W与b的偏导的形式。

（1）Loss对a(3)求导。

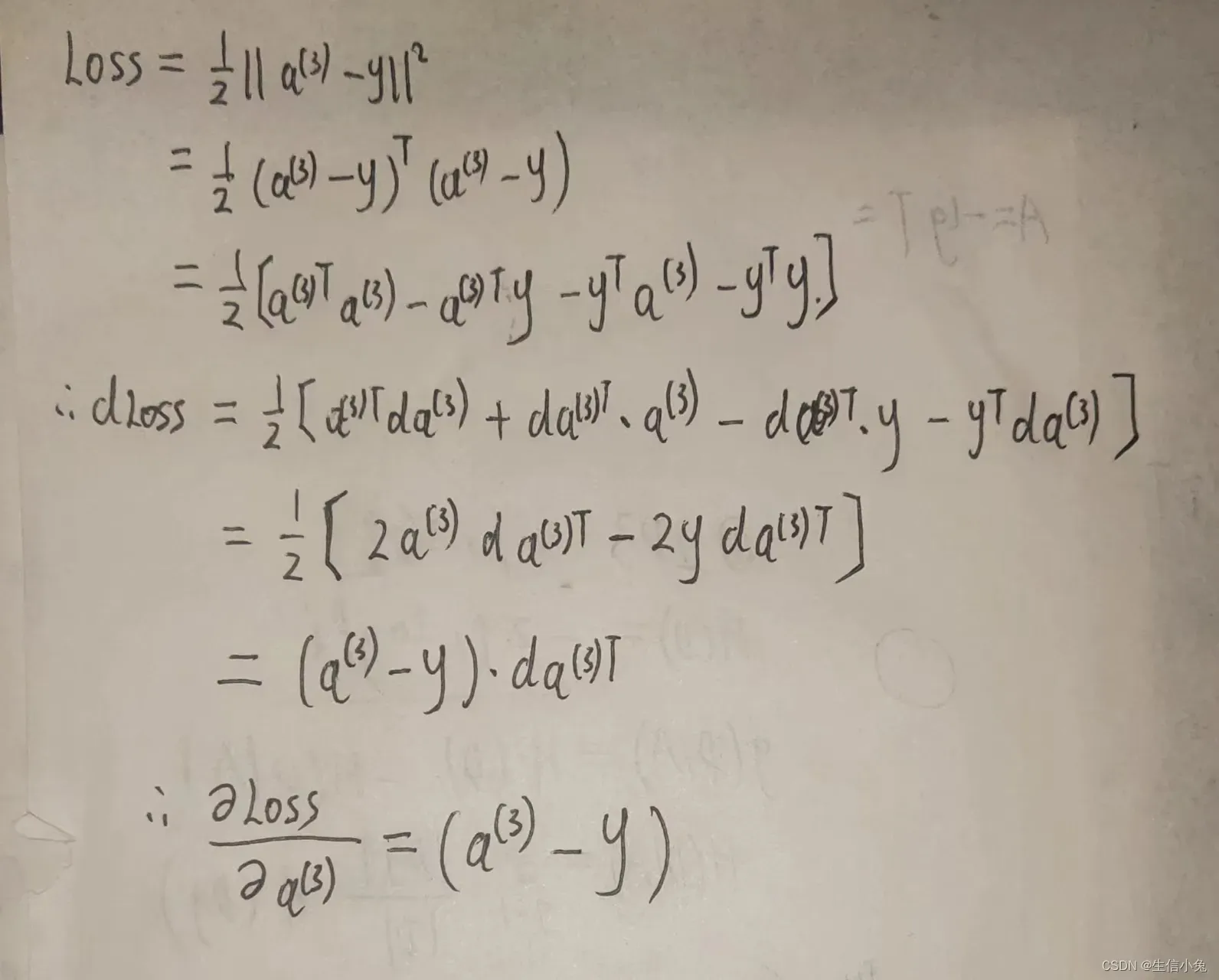
上式的最终的形式与普通的函数求导相同，只不过这里的结果是向量。

（2）a(3)对s(3)导数。

求 $\textbf{a}^{(3)}$ 对 $\mathbf{s}^{(3)}$ 的导数，这里需要注意的是，激活函数作用于向量s中的每一个数（与矩阵论中矩阵函数不同，那里是把函数展开乘幂级数，自变量是矩阵）。所以求这个导数需要先依据定义来尝试求解，发现其中的规律。

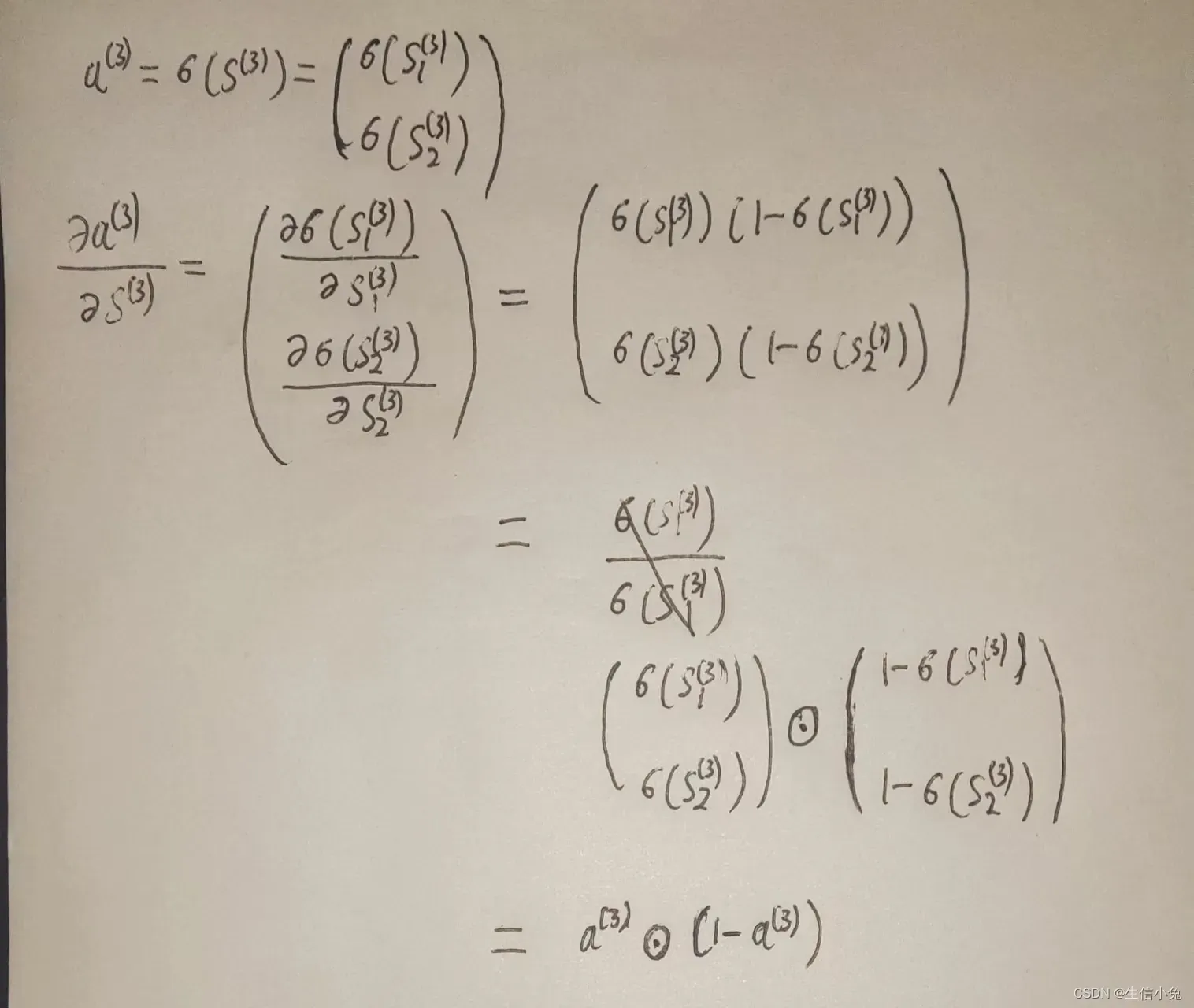
对于一元函数， $\sigma (x)'=\sigma(x).(1-\sigma(x))$ 。在这里，由于sigmoid函数作用于向量中各个元素，求导即是向量内各个元素对自变量向量中各个元素求导。所以在这里最终的形式与普通函数相一致，不过这里的乘积是哈达玛乘积（用符号 $\odot$ 或 $\circ$ 表示），表示向量或矩阵对应位置相乘，1变成了维数与a(3)相同的全1向量。

（3）s(3)对W(2)、b(2)与s(2)的导数

首先，对于s(3)对W(2)、b(2)的偏导，我们在这里需要依据这里的具体情况来推导，总结规律。

我们发现，s(3)对W(2)、b(2)的偏导是有一定的规律的。s(3)=W(2).a(2)+b(2),其对b(2)偏导是与b(2)维数相同的全1向量，类似于普通三元函数f(w,x,b)=wx+b对b求偏导等于1；s(3)对W(2)偏导，结果为 $(1,1,1)^{T}.{a^{(2)}}^{T}$ ，类似于f(w,x,b)对w偏导等于x，不过在这里是向量对矩阵求偏导，需要有矩阵或向量的转置，并且乘以全1向量。对于这种现象，我们还是以一个普通的三元函数f(w,x,b)=wx+b为例，f(w,x,b)对w的偏导可以看成是

$\frac{\partial f(w,x,b)}{\partial f(w,x,b)}.\frac{\partial f(w,x,b)}{\partial w}=1. (\frac{\partial f(w,x,b)}{\partial w})^{T}=1.x^{T}=x$

f(w,x,b)对x的偏导可以看成为：

$\frac {\partial f(w,x,b)}{\partial x}. \frac{ \partial f(w,x,b)}{\partial f(w,x,b)}=(\frac{\partial f(w,x,b)}{\partial x})^{T}.1=w^{T}.1=w$

可以看出普通的函数是矩阵的特殊情况，它所乘数值1并满足交换律，数的转置仍是这个数，所以普通函数偏导的结果如此简洁。而对于矩阵的情况，先计算函数对自己的导数，也就是全1向量或矩阵，维数与该函数维数相同（注意：这里是s(3)为W(2)、a(2)、b(2)的函数的情况，所以乘s(3)对自己的偏导，即全1向量；在链式求导过程中，s(3)作为链的一部分，此时乘的不是全1向量，而是Loss对s(3)的偏导）。之后乘函数对自变量的偏导时，如果自变量在函数内乘积的左侧，这个偏导结果就右乘，否则就是左乘。这个结论在后面的矩阵函数链式求导还会用到。

（4）链式求导

兔兔在这里先举一个具体实例：

$W^{(0)}_{a\times b}.X^{(0)}_{b\times c}=Y^{(1)}_{a\times c} \\ W^{(1)}_{d\times a}.Y^{(1)}_{a\times c}=Y^{(2)}_{d\times c} \\ W^{(2)}_{e\times d}.Y^{(2)}_{d \times c}=Y^{(3)}_{e\times c}$

其中的W、X、Y都是不同维数的矩阵，右下角代表矩阵维数。由最终的Y(3)，可以求出Y(3)分别对W(2)和Y(2)的偏导。

$\frac{\partial Y^{(3)}}{\partial W^{(2)}}=\frac{\partial Y^{(3)}}{\partial Y^{(3)}}.\frac{\partial Y^{(3)}}{\partial W^{(2)}}=(1)_{e\times c}.({Y^{(2)}}^{T})_{c\times d}$

$\frac{\partial Y^{(3)}}{\partial Y^{(2)}}=\frac{\partial Y^{(3)}}{\partial Y^{(2)}}.\frac{\partial Y^{(3)}}{\partial Y^{(3)}}=({W^{(2)}}^{T})_{d\times e}.(1)_{e\times c}$

这些是与（3）中结论一致的。之后我们求Y(3)对W(1)、Y(1)偏导时，根据链式求导法则，Y（3）对W(1)的偏导为Y(3)对Y(2)的偏导乘Y(2)对W(1)的偏导，Y(1)的偏导也是如此，不过，在这里我们还是需要注意这两个偏导相乘时的位置关系。

$\frac{\partial Y^{(3)}}{\partial Y^{(1)}}=\frac{\partial Y^{(2)}}{\partial Y^{(1)}}.\frac{\partial Y^{(3)}}{\partial Y^{(2)}}=({W^{(1)}}^{T})_{a\times d}.({W^{(2)}}^{T})_{d\times e}.(1)_{e\times c}$

$\frac{\partial Y^{(3)}}{\partial W^{(1)}}=\frac{\partial Y^{(3)}}{\partial Y^{(2)}}.\frac{\partial Y^{(2)}}{\partial W^{(1)}}=({W^{(2)}}^{T})_{d\times e}.(1)_{e\times c}.({Y^{(1)}}^{T})_{c\times a}$

如果按照一元函数那样，链式求导后各个偏导从左到右依次相乘，在矩阵求导这里会出现维数不一致而无法相乘的情况。实际的矩阵链式求导过程是：一个函数对某个自变量求偏导，如果该自变量在式子乘积的左侧，则偏导右乘函数上一层的偏导值，反之左乘。上面的例子便很好地体现这一规律。

根据上面的这些规律，我们就可以得出损失函数对各层之间是W与b的偏导值了。

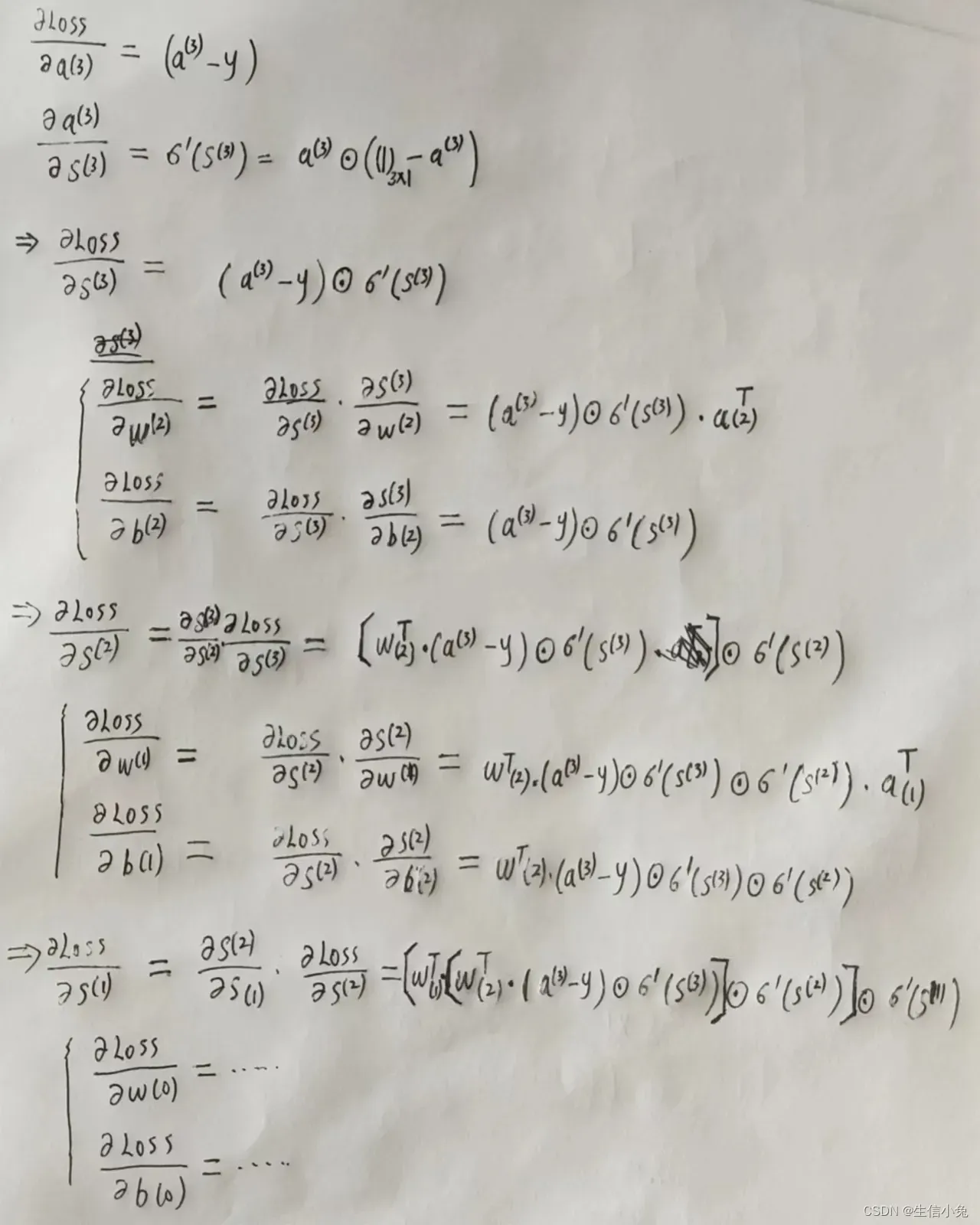
（4）总结

根据以上推导，我们最终可以得出反向传播的递推公式：

$\frac{\partial Loss}{\partial \mathbf{s}^{(l)}}=\frac{\partial \textbf{s}^{l+1}}{\partial \textbf{s}^{(l)}}.\frac{\partial Loss}{\partial \textbf{s}^{(l+1)}}=[{W^{(l)}}^{T}....{W^{(n-1)}}^{T} [(\mathbf{a}^{(n)}-y) \odot \sigma'(\textbf{s}^{(n)})]...\odot \sigma(\textbf{s}^{(l+1)}) ]\odot \sigma'(\textbf{s}^{(l)})$

$\frac{\partial Loss}{\partial W^{(l)}}=\frac{\partial Loss}{\partial \mathbf{s}^{(l+1)}}.\frac{\partial \textbf{s}^{(l+1)}}{\partial W^{(l)}}=\frac{\partial Loss}{\partial \textbf{s}^{(l+1)}}.{\mathbf{a}^{(l)}}^{T}$

$\frac{\partial Loss}{\partial \mathbf{b}^{(l)}}=\frac{\partial Loss}{\partial \mathbf{s}^{(l+1)}}$

由这三个公式，就可以从后往前依次求各个参数的梯度了。

（3）梯度下降法与参数更新

求得所有参数的梯度后，可以采用梯度下降等算法来优化参数。在这里兔兔最为普通的梯度下降方法，则参数更新递推公式为：

$W^{(l)}(t+1)=W^{(l)}(t)-\alpha .\frac{\partial Loss}{\partial W^{(l)}(t) }$

$\mathbf{b}^{(l)}(t+1)=\textbf{b}^{(l)}(t)-\alpha \frac{\partial Loss}{\partial \mathbf{b}^{(l)} (t)}$

其中t表示第t次时的参数值。α为学习率，通常学习率越小，学习速度越慢，但可能效果会好一些；学习率大，虽然参数更新速度比较快，但效果很可能会不好，甚至无法收敛到最优解。

我们发现，在更新参数过程中，其中的偏导部分的求解需要用到各层W，b，a，s数值。所以，在每次学习过程中，我们都先要利用样本数据进行一次正向传递，得到a与s的数值，利用这些数值在反向传播更新W与b。

在前面的四（1）中，我们提到了随机梯度下降，实际应用时，是每一个batch更新一次参数，即对batch中每一组数据都进行正向传递与反向传播，得到参数的梯度，最终所有的梯度求和，除以batch中样本个数得到一个较为平均的梯度，然后再更新参数W、b。

（4）算法实现

import numpy as np
class BP:
    def __init__(self,x,y,node=[4,3,2,3],batchlength=20,alpha=0.1,circle=100):
        '''略'''
        self.alpha=alpha #学习率
        self.circle=circle #学习次数
    '''略'''
    def dsigmoid(self,x):
        '''激活函数sigmoid导数'''
        return np.multiply(self.sigmoid(x),1-self.sigmoid(x))
    def train(self):
        '''训练神经网络的主程序'''
        for i in range(self.circle):
            print('the {} epoch'.format(i))
            for batch in self.batches():
                self.backprob(batch=batch) #更新参数
    def backprop(self,batch):
        '''正向传播与反向传播更新参数'''
        d_w=[np.zeros(shape=self.w[j].shape) for j in range(self.n-1)]
        d_b=[np.zeros(shape=self.b[j].shape) for j in range(self.n-1)] #导数和
        for x,y in batch:
           x=np.mat(x).T #转成列向量
           y=np.mat(y).T
           A=[x]
           S=[] #储存正向传递的a,s值
           s0=np.dot(self.w[0],x)+self.b[0]
           a0=self.sigmoid(s0)
           A.append(a0);S.append(s0)
           for i in range(1,self.n-1):
              '''正向传递'''
              s=np.dot(self.w[i],a0)+self.b[i]
              a=self.sigmoid(s)
              s0=s
              a0=a
              A.append(a0)
              S.append(s0)
           dw=[np.zeros(shape=self.w[j].shape) for j in range(self.n-1)]
           db=[np.zeros(shape=self.b[j].shape) for j in range(self.n-1)] #初始各个参数梯度为0
           db[-1]=np.multiply((A[-1]-y),self.dsigmoid(S[-1]))
           dw[-1]=np.dot(db[-1],A[-2].T)
           d_w[-1]+=dw[-1];d_b[-1]+=db[-1]
           for i in range(2,self.n-1):
              '''反向传播'''
              db[-i]=np.multiply(np.dot(self.w[-i+1].T,db[-i+1]),self.dsigmoid(S[-i]))
              dw[-i]=np.dot(db[-i],A[-i-1].T)
              d_w[-i]+=dw[-i]
              d_b[-i]+=db[-i]
        for i in range(self.n-1):
           self.w[i]-=self.alpha* d_w[i]/self.batchlength
           self.b[i]-=self.alpha* d_b[i]/self.batchlength

需要注意的是，一般的数据集中每组数据往往都是array或行向量的形式，计算时需要先转换成列向量再进行计算。

五：实际案例与算法实现

兔兔在这里以 dry bean dataset数据集为例，该数据含有13611组数据，数据含有16个指标，7个类别。则神经网络的输入层与输出层神经元个数设为16、7。先对数据集的数据作初步处理，使之能够输入该模型中。

import numpy as np
import pandas as pd
class BP:
   def __init__(self,x,y,node=[16,3,3,7],batchlength=100,alpha=0.01,circle=100):
      self.x=x #训练数据
      self.y=y #数据对应的类别
      self.w=[np.random.normal(size=(node[i+1],node[i])) for i in range(len(node)-1)]
      self.b=[np.random.normal(size=(node[i+1],1)) for i in range(len(node)-1)]
      self.n=len(node) #n为神经元层数
      self.batchlength=batchlength
      self.alpha=alpha
      self.circle=circle
   def sigmoid(self,x):
      '''激活函数'''
      return 1/(1+np.exp(-x))
   def dsigmoid(self,x):
      '''激活函数sigmoid导数'''
      return np.multiply(self.sigmoid(x),1-self.sigmoid(x))
   def forward(self,x):
      '''信号前向传递'''
      s0=np.dot(self.w[0],x)+self.b[0]
      a0=self.sigmoid(s0)
      for i in range(1,self.n-1):
         s=np.dot(self.w[i],a0)+self.b[i]
         a=self.sigmoid(s)
         a0=a
      return a0
   def batches(self):
      '''把数据集分成长度为batchlength的各个batch'''
      data=list(zip(self.x,self.y))
      np.random.shuffle(data)
      batches=[data[i:i+self.batchlength]for i in range(0,len(data),self.batchlength)]
      return batches
   def train(self):
      '''训练神经网络主程序'''
      for i in range(self.circle):
         print('the {} epoch'.format(i))
         for batch in self.batches():
            self.backprop(batch=batch)
   def backprop(self,batch):
      '''正向传播与反向传播更新参数'''
      d_w=[np.zeros(shape=self.w[j].shape) for j in range(self.n-1)]
      d_b=[np.zeros(shape=self.b[j].shape) for j in range(self.n-1)] #导数和
      for x,y in batch:
         x=np.mat(x).T #转成列向量
         y=np.mat(y).T
         A=[x]
         S=[] #储存正向传递的a,s值
         s0=np.dot(self.w[0],x)+self.b[0]
         a0=self.sigmoid(s0)
         A.append(a0);S.append(s0)
         for i in range(1,self.n-1):
            '''正向传递'''
            s=np.dot(self.w[i],a0)+self.b[i]
            a=self.sigmoid(s)
            s0=s
            a0=a
            A.append(a0)
            S.append(s0)
         dw=[np.zeros(shape=self.w[j].shape) for j in range(self.n-1)]
         db=[np.zeros(shape=self.b[j].shape) for j in range(self.n-1)] #初始各个参数梯度为0
         db[-1]=np.multiply((A[-1]-y),self.dsigmoid(S[-1]))
         dw[-1]=np.dot(db[-1],A[-2].T)
         d_w[-1]+=dw[-1];d_b[-1]+=db[-1]
         for i in range(2,self.n-1):
            '''反向传播'''
            db[-i]=np.multiply(np.dot(self.w[-i+1].T,db[-i+1]),self.dsigmoid(S[-i]))
            dw[-i]=np.dot(db[-i],A[-i-1].T)
            d_w[-i]+=dw[-i]
            d_b[-i]+=db[-i]
      for i in range(self.n-1):
         self.w[i]-=self.alpha*d_w[i]/self.batchlength
         self.b[i]-=self.alpha*d_b[i]/self.batchlength
   def predict(self,x):
      '''预测未知类别数据的类别'''
      a=self.forward(x)
      return a
if __name__=='__main__':
   df=pd.DataFrame(pd.read_csv('Dry_Bean_Dataset.csv'))
   x=np.array(df.loc[0:13610,'Area':'ShapeFactor4'])
   y=[]
   for i in df['Class']:
      if i =='SEKER':
         y.append(np.array([1,0,0,0,0,0,0]))
      elif i=='BARBUNYA':
         y.append(np.array([0,1,0,0,0,0,0]))
      elif i=='BOMBAY':
         y.append(np.array([0,0,1,0,0,0,0]))
      elif i=='CALI':
         y.append(np.array([0,0,0,1,0,0,0]))
      elif i=='HOROZ':
         y.append(np.array([0,0,0,0,1,0,0]))
      elif i=='SIRA':
         y.append(np.array([0,0,0,0,0,1,0]))
      else:
         y.append(np.array([0,0,0,0,0,0,1]))
   bp=BP(x=x,y=y).train()

一般情况下，我们把数据集分成训练集与测试集，在使用训练集模型训练完成后，再使用测试集，看模型准确率是否较高，然后条件学习率、学习次数等各种参数，提高模型的准确率与学习速度。

除了分类问题，这个神经网络也是可以进行函数的拟合与预测等。在这个神经网络中，由于输出的值域为（0，1），所以可以用它拟合一下值域（0，1）的一元函数或多元函数等。如使用一群在函数曲线f(x)=(1+cosx)/2的数据点，输入到输入层与输出层神经元个数都为1的神经网络中进行训练，可以测试训练过程中预测曲线与实际的曲线差别，效果大致如下。

六：总结

BP神经网络作为一种最为基础的深度学习算法，虽然在一些问题中有较好的效果，但是其问题也十分明显。首先，它的运算量很大，对计算机硬件要求较高；其次，很多情况下，它的效果也不是很好，学习时间较长，需要很多的数据去训练，预测准确率不高，与支持向量机等机器学习方法相比效果也差很多，这也是为什么在很长一段时间神经网络几乎没有太大的发展。BP神经网络虽然有诸多的不足，却是其它更加复杂、效果更优的神经网络的基础，例如在卷积神经网络（CNN）中，该神经网络以全连接层的身影出现，在循环、递归神经网络（RNN）、长短期记忆网络（LSTM）等神经网络中，也都体现着BP神经网络的基本思想。

补充内容：

（1）该神经网络的算法实现方法很多，例如逐层传递的过程，可以将b,w先用zip函数处理，再使用循环逐个从zip中取出使用，代码行数会减少许多。

（2）激活函数在神经网络中有着重要意义。与生物的神经元相类比，它对应着该神经细胞是否兴奋，是否能够向下一个神经元发出信号；从计算的角度，如果没有sigmoid将数值限制在0~1之间，逐层传递时不断累加，最终的数值会非常的大。

（3）在分类问题中，隐藏层可以使用sigmoid函数，但是在最后一层使用softmax激活函数，本文为了讲解方便，激活函数只使用了sigmoid。

（4）在本文矩阵求导的过程中，需要注意函数对一个自变量的导数的维数与该自变量的维数是一致的，如果推导过程中发现有维数不一致的情况，则推导错误。

（5）本文所使用的数据集数据较多，采用随机梯度下降算法，可以每次随机从样本中选取个数为batchlength的数据进行学习，并且注意计算过程中指数函数的溢出问题。

文章出处登录后可见！

已经登录？立即刷新

多层感知机（MLP）、全连接神经网络（FCNN）、前馈神经网络（FNN）、深度神经网络（DNN）与BP算法详解

一：概念辨析

二：BP神经网络生物学原理

三：BP神经网络结构与信号（数据）传递

（1）训练数据集的特征

（2）BP神经网络结构

（3）总结

（4）算法实现

四：BP算法

（1）损失函数的构造与数据集训练方法

（2）损失函数对W与b的偏导数求解

（3）梯度下降法与参数更新

（4）算法实现

五：实际案例与算法实现

六：总结

相关推荐