前言
1)说起卡尔曼滤波,必有状态空间模型,两个离不开。
2)从卡尔曼滤波名字就可以看出来,其更倾向于滤波。即对系统噪声和测量噪声进行过滤优化,得出更优的结果。如果系统噪声比较强,那么最终结果就会倾向于测量结果,而当测量噪声强时,最终结果就倾向于系统状态方程描述的结果。
3)卡尔曼滤波是个迭代计算过程,不断重复这两步,预测和校正(更新)。校正就是用测量结果和状态方程结果不断计算卡尔曼增益K。K越大越详细测量结果,K越小越相信状态方程描述的结果。
4)卡尔曼滤波必须先知道系统状态方程,只有对系统较为熟悉才能写出。所以不知道系统时,采用最小二乘法,而不是卡尔曼滤波。如果状态方程写错了,卡尔曼滤波效果也许并不好。
1.状态空间模型
状态空间模型 (State Space Model),包括两个方程模型:
一是状态方程模型,反映动态系统在输入变量作用下在某时刻所转移到的状态;
二是输出或测量方程模型,它将系统在某时刻的输出和系统的状态及输入变量联系起来。
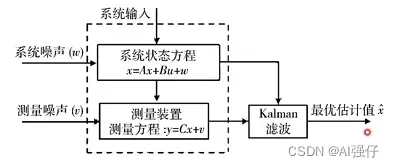
状态空间模型求解算法的核心是Kalman滤波。
2.卡尔曼滤波
卡尔曼滤波的目的:由于人的主观认识(数学模型的建立而产生的理论状态值)和测量(传感器等测量值)都不准确,引入卡尔曼滤波,综合两者的误差,得到最优的对于真实值的预测。
以前有一种状态估计方法称为维纳滤波,它在第二次世界大战期间得到了应用。其缺点在于:①必须使用全部的历史观测数据,存储量和计算量都很大;②当获得新的观测数据时,没有合适的递推算法;③很难用于非平稳过程的滤波问题。为克服上述缺点,在20世纪60年代初,美国数学家R.E.卡尔曼(R.E.Kalman)等人发展了一种递推滤波方法,即现称的卡尔曼滤波。
斯坦利·施密特(Stanley Schmidt)首次实现了卡尔曼滤波器。卡尔曼在NASA埃姆斯研究中心访问时,发现他的方法对于解决阿波罗计划的轨道预测很有用,后来阿波罗飞船的导航电脑使用了这种滤波器。 关于这种滤波器的论文由Swerling (1958), Kalman (1960)与 Kalman and Bucy (1961)发表。
Kalman滤波算法的本质就是利用两个正态分布的融合仍是正态分布这一特性进行迭代而已。比如两个秤去测量一个苹果的重量,每个秤的测量存在误差,是正态分布。两个秤就是两个正态分布。那么我们将两个秤的结果通过某种算法合并就能得到更真实的苹果重量,而不是相信其中一个秤。

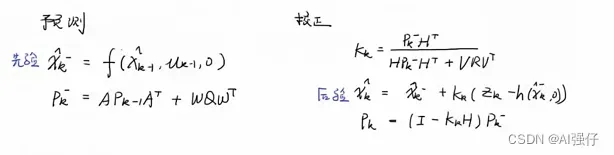
卡尔曼滤波核心公式如下:

不考虑u及B时,简写为:

公式推导参见,【【卡尔曼滤波器】1_递归算法_Recursive Processing-哔哩哔哩】 https://b23.tv/XOOAYUK.
3.扩展卡尔曼滤波(EKF)
当状态方程和测量方程非线性方程时,就考虑扩展卡尔曼滤波。
对于非线性滤波,至今未得到完善的解法,通常的处理方法是利用线性化技巧将非线性滤波问题转化为一个近似的线性滤波问题,套用线性滤波理论得到求解原非线性滤波问题的次优滤波算法,其中最常用的线性化方法是泰勒级数展开,得到的滤波方法即为扩展卡尔曼滤波。对于二阶EKF,其滤波性能远比一阶的要好,但是二阶以上的效果提升就不明显了,所以一般就是用一阶、二阶,但是二阶计算量比较大,一般都用一阶的。
4.状态空间模型与ARMAX
1)每一个有外部变量的自回归移动平均系统(ARMAX)或可用有理传递函数表示的系统都可以转换成用状态空间表示的系统,从而能用卡尔曼滤波进行计算。但是只有简单的状态空间模型可以以ARIMA形式精确表示。
2)与ARIMA相比,状态空间模型使您可以对更复杂的流程进行建模,具有可解释的结构并轻松处理数据不规则性;但是为此,您需要付出的代价是增加模型的复杂性,更难进行校准。
5.Kalman与最小二乘法
最小二乘(Least Square)是优化方法中的一种特殊情况,而卡尔曼滤波又是最小二乘法的一种特殊情况。 古典最小二乘中,假设了每一次测量的权重相同,但事实上这样并不合理,后来演化为加权最小二乘法,至此最小二乘估计所做的都是批处理(Batch),这样比较占内存,不符合动态系统状态估计的需要,即每一次更新输入时,都要从新计算之前所有的记录值。而后,提出递推最小二乘法,模型就不用每次都重新计算了。与递归最小二乘相似,卡尔曼滤波加入了系统内部变化的考虑。即利用process model对系统在下一时刻的状态进行预测。
当对于系统不够了解时,使用最小二乘法比较合适,而对于系统了解比较多时,可以采用Kalman滤波。改变量测噪声、系统噪声都会对Kalman滤波的效果产生影响,而不会对最小二乘滤波产生影响,而改变最小二乘的阶数会对其产生影响.
6.Kalman与HMM
HMM 模型适用于隐变量是离散的值的时候,对于连续隐变量的 HMM,常用卡尔曼滤波(Kalman Filtering)描述线性高斯模型的状态变量,使用粒子滤波(Particle Filter)来表述非高斯非线性的状态变量。
《Advanced Digital Signal Processing and Noise Reduction 4th Edition》中的描述:

7.代码
可以参考开源git:http://github.com/rlabbe/filterpy
import numpy as np
import matplotlib.pyplot as plt
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
np.random.seed(2)
def demo():
dt = 0.1
F = np.array([[1, dt], [0, 1]])
Q = 1e-2 * np.array([[1 / 4 * dt ** 4, 1 / 2 * dt ** 3], [1 / 2 * dt ** 3, dt ** 2]])
R = 2.
itr = 100
real_state = []
x = np.array([10, 5]).reshape(2, 1)
for i in range(itr):
real_state.append(x[0, 0])
x = np.dot(F, x) + np.random.multivariate_normal(mean=(0, 0), cov=Q).reshape(2, 1)
measurements = [x + np.random.normal(0, R) for x in real_state]
# initialization
P = np.array([[10, 5], [5, 10]])
x = np.random.multivariate_normal(mean=(10, 5), cov=P).reshape(2, 1)
# filter
kf = KalmanFilter(dim_x=2, dim_z=1) # dim_x:隐状态大小,dim_z:量测大小
# 定义参数
kf.x = x # 初始状态[位置,速度]
kf.F = F # 状态转移矩阵
kf.H = np.array([[1., 0.]]) # 量测矩阵
kf.P = P # 初始状态协方差
kf.R = R # 量测噪声
kf.Q = Q_discrete_white_noise(dim=2, dt=dt, var=1e-2) # 过程(系统)噪声
filter_result = list()
filter_result.append(x)
for i in range(1, itr):
z = measurements[i]
kf.predict()
kf.update(z)
filter_result.append(kf.x)
filter_result = np.squeeze(np.array(filter_result))
return measurements, real_state, filter_result
8.参考
1)部分公式来源于:【【卡尔曼滤波器】1_递归算法_Recursive Processing-哔哩哔哩】 https://b23.tv/XOOAYUK.
2)卡尔曼滤波(kalman)相关理论以及与HMM、最小二乘法关系https://blog.51cto.com/u_13206712/5839786
3)《Advanced Digital Signal Processing and Noise Reduction 4th Edition》
文章出处登录后可见!
