相空间重构
1 特征描述
相空间重构的基本思想为:系统中任意变量的变化过程由与之相互作用的分量共同决定,其发展过程也隐含着其他变量的变化规律,故可从变量的变化过程中构建和恢复整个系统的变化规律。针对序列,通过坐标延迟重构法,可以将序列映射到一个
维的相空间中,重构后的轨迹矩阵如下。
上式中,为时间延迟参数;
为嵌入维数,每一行可视为相空间中的一个相点的坐标;重构的相空间轨迹由
个相点组成。
的大小取决于
和
,
。
相空间重构的核心问题在于如何选择合适的时间延迟参数和嵌入维数
。
太小会使相点分布过于密集,太大则过于分散;
过大会增大计算量,过小则难以显示隐藏特征。
一般嵌入维数可根据具体课题选定,例如使用二维轨迹图来提取特征进行研究,则直接选择
为
。而时间延迟参数
可以使用自相关函数进行计算,当自相关函数值达到第一次极小值或近似为零时,此时的
比较合适。若有多个信号序列,为简化计算,可取所有序列的合适
值的平均值作为设定的时间延迟参数
。定义自相关函数如下。
其中,为时间序列的均值。
2 数据来源
提供一串信号的数据:
这组数据存在三个频率分量,分别为100Hz,200Hz和300Hz, 用MATLAB生成。
# 定义三个频率分量的参数
t = 0:0.0001:2/100;
freq1 = 100; # 第一个频率分量的频率(Hz)
freq2 = 200; # 第二个频率分量的频率(Hz)
freq3 = 300; # 第三个频率分量的频率(Hz)
# 生成三个频率分量的正弦波信号
signal1 = sin(2 * pi * freq1 * t);
signal2 = sin(2 * pi * freq2 * t);
signal3 = sin(2 * pi * freq3 * t);
# 将三个频率分量的信号相加
result = signal1 + signal2 + signal3;
3 函数的Python代码
3.1 Python库要求
import numpy as np
3.2 PhaseSpaceReconstruction(inputS, dd, tt)相空间重构函数
其中,inputS为输入的信号序列,dd为嵌入维度,tt为延迟参数。当tt为-1时,相空间重构函数会按照自相关函数计算合适的延迟参数,若tt为任意正整数,则相空间重构函数会根据用户输入的延迟参数进行相空间重构。函数的返回值matrixX为numpy类型的轨迹矩阵,每一行是一个相空间中的相点。
def PhaseSpaceReconstruction(inputS, dd, tt):
data = []
for i in inputS:
data.append(float(i))
length = len(data)
xave = np.mean(data)
Cup, Cdown, Clast = 0x3f3f3f3f, 1, 0
besttau = 0
# 计算合适的tau
if tt == -1:
for tau in range(1, length):
Clast = (Cup / Cdown)
Cup, Cdown = 0, 0
for i in range(0, length - tau):
Cup = Cup + (data[i] - xave) * (data[i + tau] - xave)
Cdown = Cdown + (data[i] - xave) * (data[i] - xave)
if (Cup / Cdown) > Clast:
besttau = tau - 1
break
else:
besttau = tt
P = length - besttau * (dd - 1)
maxdata, mindata = max(data), min(data)
# 归一化
for i in range(0, length):
data[i] = (data[i] - mindata) / (maxdata - mindata)
matrixX = np.zeros((P, dd))
for i in range(0, P):
for j in range(0, dd):
matrixX[i, j] = data[i + besttau * j]
return matrixX
3.3 相空间重构函数PhaseSpaceReconstruction(inputS, dd, tt)验证
dd = 2
inputS = input().split()
matrixX = PhaseSpaceReconstruction(inputS, dd, 10)
for i in range(0, matrixX.shape[1]):
for j in matrixX[:,i]:
print("{} ".format(j), end='')
print()
print()
4 函数的C++代码
4.1 C++库要求
#include<iostream>
#include<fstream>
#include<vector>
#include<algorithm>
4.2 void PhaseSpaceReconstruction(vector<double> sequenceX, vector<vector<double>> &matrixX, int d, int tau)相空间重构函数
其中,sequenceX为输入的信号序列,d为嵌入维度,tau为延迟参数。当tau为-1时,相空间重构函数会按照自相关函数计算合适的延迟参数,若tau为任意正整数,则相空间重构函数会根据用户输入的延迟参数进行相空间重构。matrixX为vector<vector<double>>类型的轨迹矩阵,每一行是一个相空间中的相点。
void PhaseSpaceReconstruction(vector<double> sequenceX, vector<vector<double>> &matrixX, int d, int tau) {
int length = sequenceX.size();
if (tau == -1) {
auto besttau = [length](vector<double> sequenceX) -> int {
double xsum = 0., xave = 0.;
double Cup = double(0x3f3f3f3f), Cdown = 1., Clast = 0.;
for (auto i : sequenceX) xsum += i;
xave = xsum / double(length);
for (size_t tau = 1; tau < length; tau++) {
Clast = Cup / Cdown;
Cup = 0., Cdown = 0.;
for (size_t i = 0; i < (length - tau); i++) {
Cup = Cup + (sequenceX[i] - xave) * (sequenceX[i + tau] - xave);
Cdown = Cdown + (sequenceX[i] - xave) * (sequenceX[i] - xave);
}
if ((Cup / Cdown) > Clast) {
return (tau - 1);
}
}
return -1;
};
tau = besttau(sequenceX);
}
int P = length - tau * (d - 1);
double maxX = *max_element(sequenceX.begin(), sequenceX.end());
double minX = *min_element(sequenceX.begin(), sequenceX.end());
for (auto & i : sequenceX) i = (i - minX) / (maxX - minX);
vector<double> vtemp;
for (size_t i = 0; i < P; i++) {
for (size_t j = 0; j < d; j++) {
vtemp.emplace_back(sequenceX[i + tau * j]);
}
matrixX.emplace_back(vtemp);
vtemp.clear();
}
return;
}
4.3 相空间重构函数void PhaseSpaceReconstruction(vector<double> sequenceX, vector<vector<double>> &matrixX, int d, int tau)验证
int main() {
vector<double> sequenceX; //N个
vector<vector<double>> matrixX; //P行d列
int NN, dd, tt;
NN = 201; //数据个数
dd = 2; //嵌入维数
tt = 10; //时间延迟参数
double temp;
fstream fs;
//从文件读
fs.open("PhaseSpaceReconstructionINPUTDATA.txt", ios::in);
if (!fs.is_open()) {
cout << "no txt file" << endl;
return -1;
}
while (fs >> temp) {
sequenceX.emplace_back(temp);
}
fs.close();
PhaseSpaceReconstruction(sequenceX, matrixX, dd, tt);
//输出至文件
fs.open("PhaseSpaceReconstructionOUTPUTDATA.txt", ios::out);
for (size_t i = 0; i < dd; i++) {
for (auto j : matrixX) fs << j[i] << " ";
fs << endl << endl;
}
fs.close();
return 0;
}
5 函数的MATLAB代码
5.1 PhaseSpaceReconstruction相空间重构函数
其中,result为输入的信号序列,d为嵌入维度,tau为延迟参数。当tau为-1时,相空间重构函数会按照自相关函数计算合适的延迟参数,若tau为任意正整数,则相空间重构函数会根据用户输入的延迟参数进行相空间重构。函数的返回值matrixX为相空间重构的轨迹矩阵,每一行是一个相空间中的相点。
function matrixX = PhaseSpaceReconstruction(result, d, tau)
% 相空间重构
%
% matrixX为输出相点矩阵
% result为信号序列
% d为嵌入维数
% tau为时间延迟参数
% tau为-1时由程序计算合适的tau
Cup = 1061109567;
Cdown = 1;
Clast = 0;
len = length(result);
xave = mean(result);
if tau == -1
for tau = 1 : (len - 1)
Clast = Cup / Cdown;
Cup = 0;
Cdown = 0;
for i = 1 : (len - tau)
Cup = Cup + (result(i) - xave) * (result(i + tau) - xave);
Cdown = Cdown + (result(i) - xave) * (result(i) - xave);
end
if (Cup / Cdown) > Clast
tau = tau - 1;
break
end
end
end
maxR = max(result);
minR = min(result);
resultONE = (result - minR) / (maxR - minR);
P = len - tau * (d - 1);
matrixX = zeros(P, d);
for i = 1 : P
for j = 1 : d
matrixX(i, j) = resultONE(i + tau * (j - 1));
end
end
end
5.2 相空间重构函数PhaseSpaceReconstruction验证
result = \\* 输入样本数据 *\\;
matrixX = PhaseSpaceReconstruction(result, 2, 10);
plot(matrixX(:, 1), matrixX(:, 2))
6 结果
6.1 Python绘制的相空间重构图像
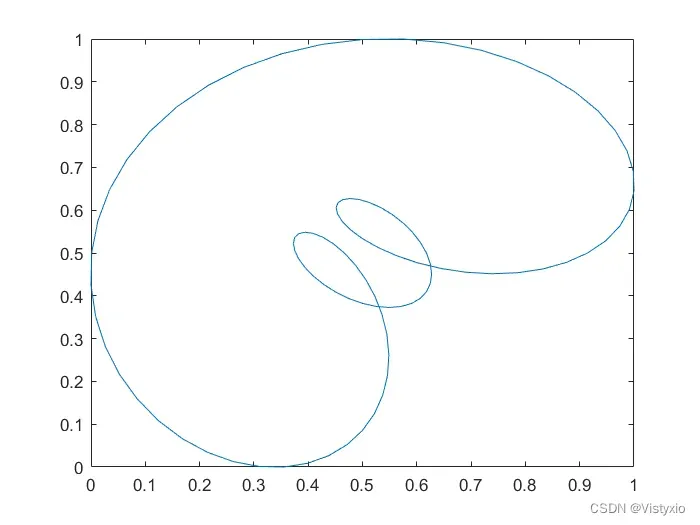
6.2 C++绘制的相空间重构图像
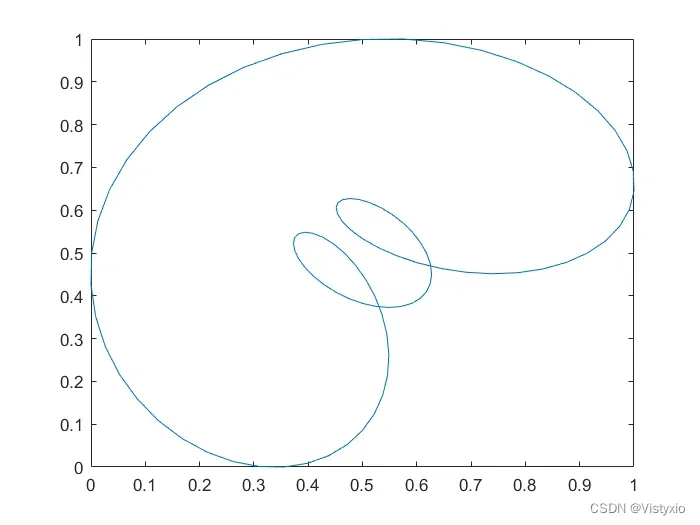
6.3 MATLAB绘制的相空间重构图像
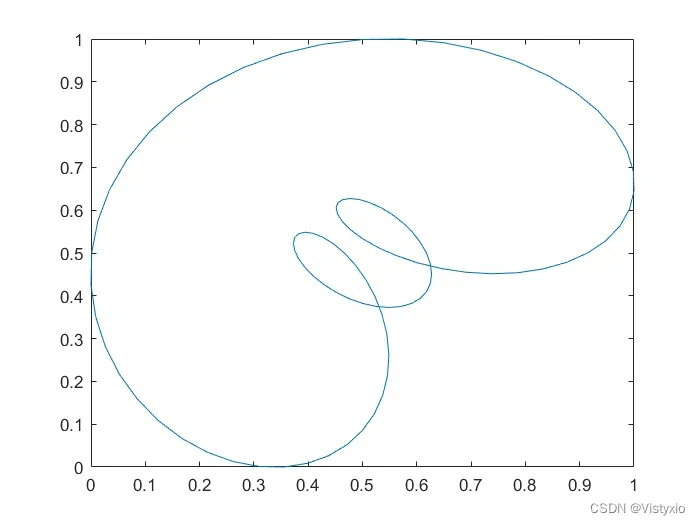
版权声明:本文为博主作者:Vistyxio原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/weixin_45715390/article/details/136527188
