注:本文是小编学习实战心得分享,欢迎交流讨论!话不多说,直接附上代码和图示说明。
目录
一、分段示例
1.导入必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn2.读取数据,查看数据基本信息
可以看到,该数据文件大小为731*7,具体信息如图所示,并发现没有缺失值
df=pd.read_csv('C:/Users/27812/Desktop/2-day.csv')
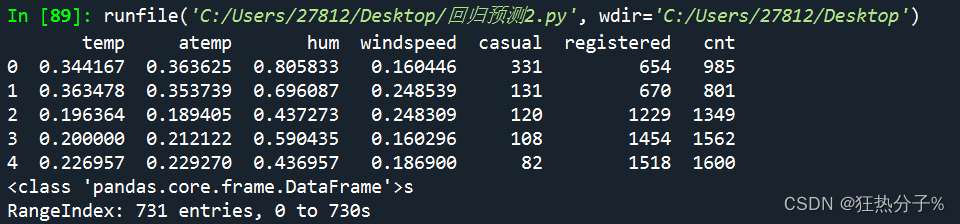
print(df.head(5))
print(df.info())#查看后发现没有缺失值
print(df.nunique())#除了前两列,其余每列都有重复值
print(df.describe())#查看数据的描述性信息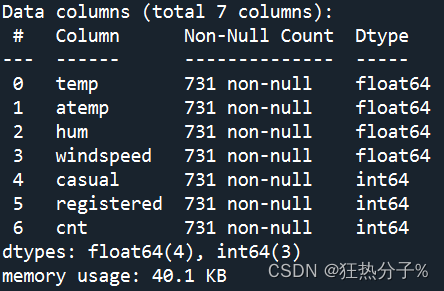
3.简单查看有无重复值
print(df[all_colums].nunique())
#提取重复值
print(df[df.duplicated()])#结果发现无重复值4.对列名进行分类,便于后面的操作,其中最后一列为预测标签数据
x_colums=['temp','atemp','hum','windspeed','casual','registered']
y_colums=['cnt']
all_colums=['temp','atemp','hum','windspeed','casual','registered','cnt']5.对数据进行初步可视化
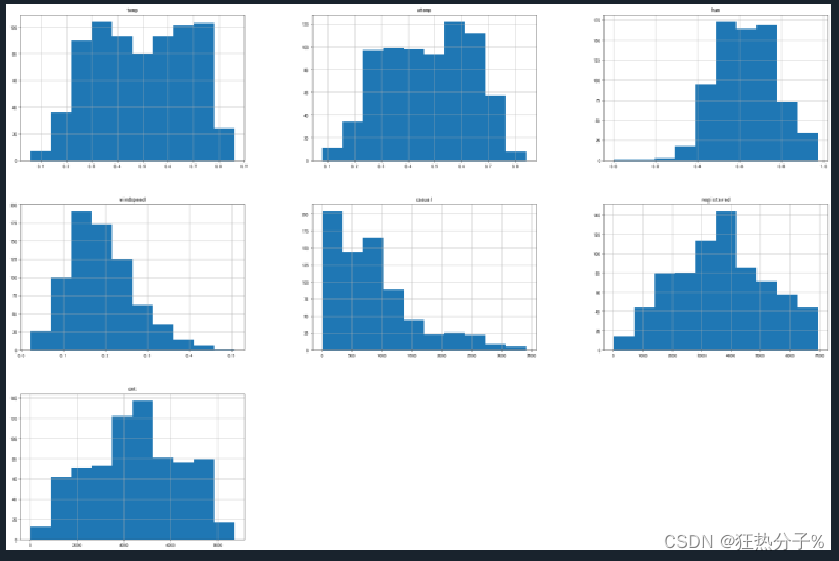
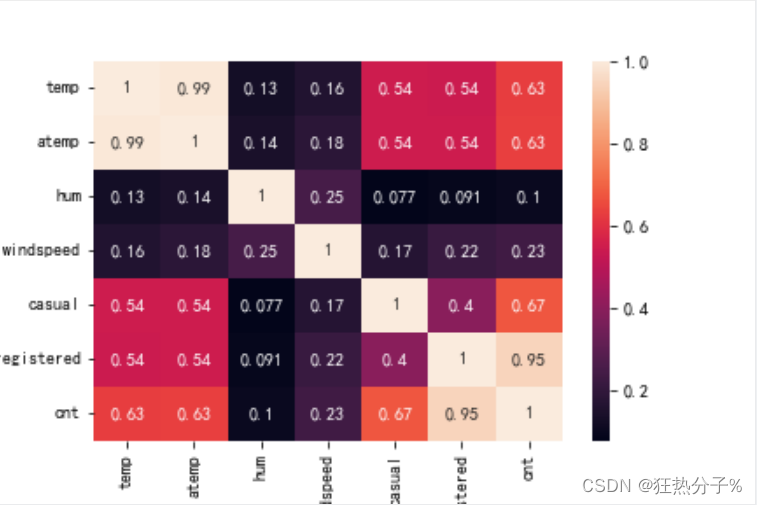
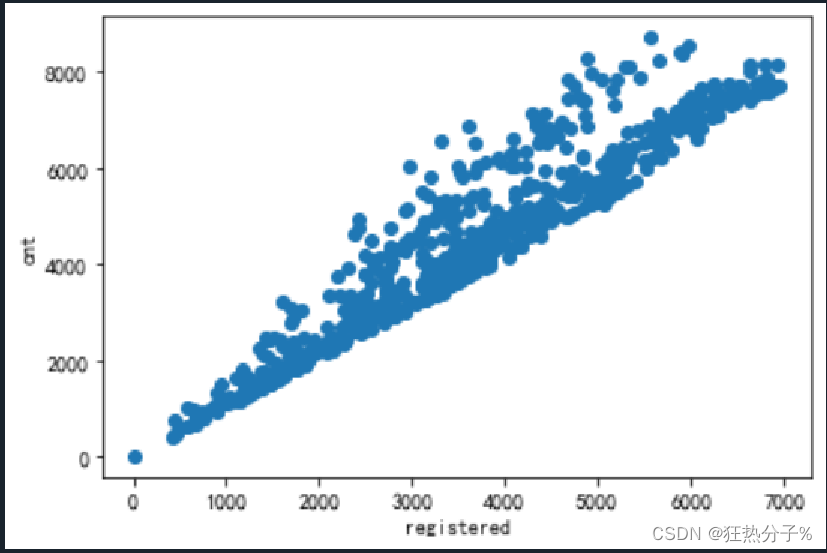
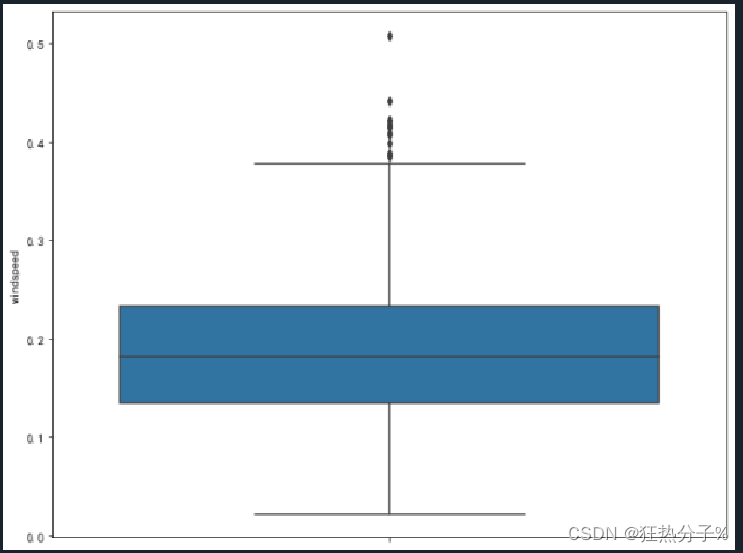
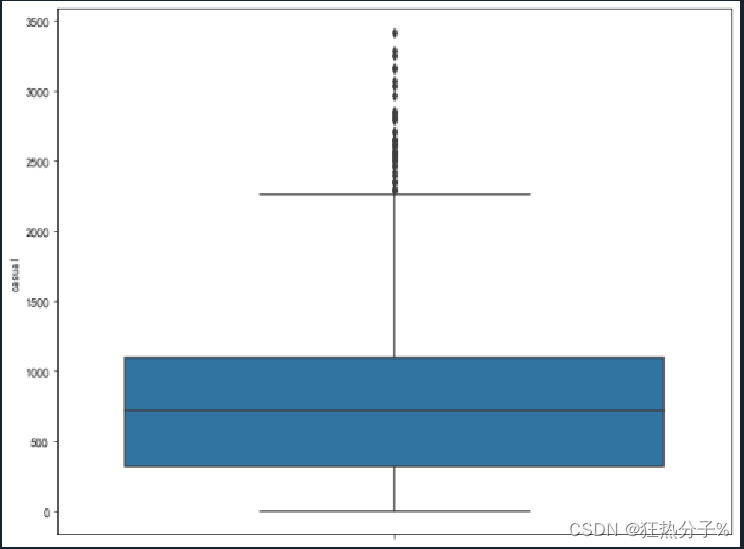
分别绘制直方图、散点图以及特征之间的相关表示图,对数据的分布以及特征之间的关系有了初步的了解或判断;同时检测异常值,并通过箱线图可视化。(展示部分图片)
#数据初步可视化
#绘制直方图
def hist(df):
df.hist(figsize=(30,20))
plt.show()
plt.savefig('a.png')
hist(df[all_colums])
#绘制散点图
def scatter(df):
for i in all_colums[:6]:
plt.scatter(df[i],df['cnt'])
plt.xlabel(i)
plt.ylabel('cnt')
plt.show()
scatter(df)
#相关系数查看特征与特征,特征与响应的线性关系
def corr_view():
data_corr=df.corr()
data_corr=data_corr.abs()
sns.heatmap(data_corr,annot=True)
plt.savefig('b.png')
corr_view()
#异常值可视化
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
for i in all_colums:
f,ax=plt.subplots(figsize=(10,8))
sns.boxplot(y=i,data=df,ax=ax)
plt.show()
plt.savefig('c.png', dpi=500)
#经发现,'hum','windspeed','casual'这三列中有异常值 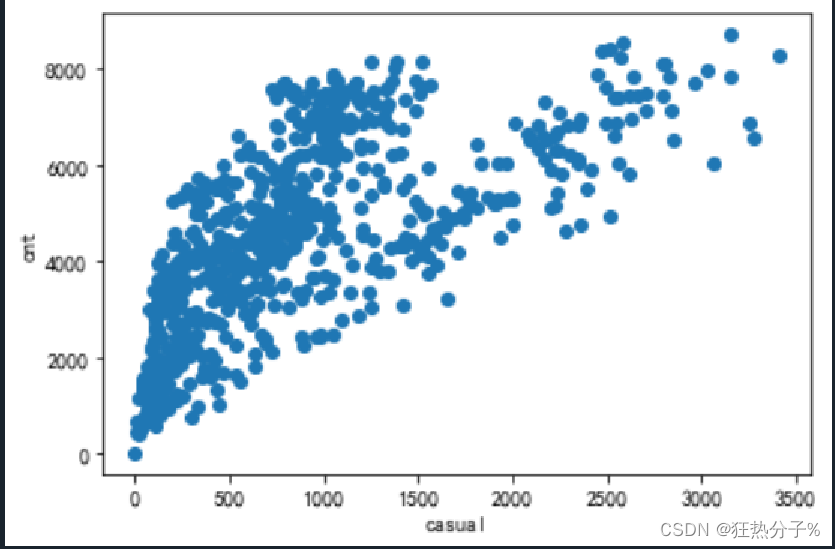
6.清除异常值
#异常值处理
# 通过Z-Score方法判断异常值,阙值设置为正负2
# 复制一个用来存储Z-score得分的数据框,常用于原始对象和复制对象同时进行操作的场景
df_zscore = df.copy()
for col in all_colums:
df_col = df[col]
z_score = (df_col - df_col.mean()) / df_col.std() # 计算每列的Z-score得分
df_zscore[col] = z_score.abs() > 2 # 判断Z-score得分绝对值是否大于2,大于2即为异常值
print(df_zscore)#显示为True的表示为异常值
# 剔除异常值所在的行
print(df[df_zscore['hum'] == False])
print(df[df_zscore['windspeed'] == False])
print(df[df_zscore['casual'] == False])#最终得到679x7的数列7.将清洗完毕的数据,放进一个文件中
注意:新产生的这个文件,不能在打开的同时运行代码,否则因为占用文件而报错
#将清洗后的数据写入新的文件,命名为new_df
new_df=df[df_zscore['casual'] == False]
new_df.to_csv('new_df.csv')8.特征选择
#特征选择
#这里选择基于Filter(过滤法)中的卡方检验
from sklearn.feature_selection import chi2, SelectKBest
feutures=['temp','atemp','hum','windspeed','casual','registered']
X, y = new_df[feutures],new_df['cnt']
chi2_model = SelectKBest(chi2, k=3)
# 以下方法返回选择后的特征矩阵
chi2_model.fit_transform(X, y)
for i in range(X.shape[1]):
print((chi2_model.scores_[i], chi2_model.pvalues_[i]))
#可以发现,'casual','registered'这两个特征与目标'cnt'关系密切
final_df=new_df.loc[:,['casual','registered','cnt']]
final_df.to_csv('final_df.csv')
#再将最终有效数据放入新文件final_df中
9.数据归一化
基于距离计算的算法模型,需要将数据归一化,便于模型的运算
#归一化;归一化通常有两种:最值归一化和均值方差归一化,这里采用均值方差归一化
from sklearn import preprocessing
from sklearn.preprocessing import StandardScaler
scaler=preprocessing.StandardScaler().fit(final_df)
final_df_scaler=scaler.transform(final_df)
print(final_df_scaler)
print(final_df_scaler.shape)
#(679, 3)10.进行训练集与测试集划分
#对新文件训练集与测试集划分
from sklearn.model_selection import train_test_split
#random_state:设置随机种子,保证每次运行生成相同的随机数
train_set,test_set = train_test_split(final_df_scaler, test_size=0.2, random_state=42)
x_train=train_set[:,0:2]
y_train=train_set[:,2]
x_test=test_set[:,0:2]
y_test=test_set[:,2]
print(x_train.shape)
print(y_test.shape)
print(y_train.dtype)11.线性回归模型训练
#进行模型训练
#1.线性回归
from sklearn import linear_model
#from sklearn import model_selection
from sklearn.linear_model import LinearRegression
def test_LinearRegression():
linearRegression = linear_model.LinearRegression()
#进行训练
linearRegression.fit(x_train, y_train)
#通过LinearRegression的coef_属性获得权重向量,intercept_获得b的值
print("权重向量:%s, b的值为:%.2f" % (linearRegression.coef_, linearRegression.intercept_))
#计算出损失函数的值
print("损失函数的值: %.2f" % np.mean((linearRegression.predict(x_test) - y_test) ** 2))
#计算预测性能得分
print("预测性能得分: %.2f" % linearRegression.score(x_test, y_test))
test_LinearRegression()
#权重向量:[0.26697613 0.85123791], b的值为:-0.00
#损失函数的值: 0.00
#预测性能得分: 1.0012.使用支持向量机(SVM)进行回归预测
注意:需将原数据类型float转化成整数类型int,否则会报错
#2.使用非线性支持向量机(SVM)进行回归预测
from sklearn.svm import SVC
from sklearn import metrics
svm_model=SVC()#SVM分类器
svm_model.fit(x_train.astype("int"),y_train.astype("int"))#注:需要将数据类型转化为int型
prediction=svm_model.predict(x_test.astype("int"))
print('准确率为:',metrics.accuracy_score(prediction, y_test.astype("int")))
#准确率为: 0.9191176470588235二、完整代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn
df=pd.read_csv('C:/Users/27812/Desktop/2-day.csv')
print(df.head(5))
print(df.info())#查看后发现没有缺失值ss
print(df.nunique())#除了前两列,其余每列都有重复值
print(df.describe())#查看数据的描述性信息
x_colums=['temp','atemp','hum','windspeed','casual','registered']
y_colums=['cnt']
all_colums=['temp','atemp','hum','windspeed','casual','registered','cnt']
print(df[all_colums].nunique())
#提取重复值
print(df[df.duplicated()])#无重复值
'''
#这步,若前面发现数值有缺失值,可用这个代码进一步查看缺失值情况
print(df[category_colums].isnull().sum())
print(df[numeric_colums].isnull().sum())
#对缺失值进行标注为-1
df[numeric_colums]=df[numeric_colums].fillna(-1)
df[category_colums]=df[category_colums].fillna(-1)
'''
#数据初步可视化
#绘制直方图
def hist(df):
df.hist(figsize=(30,20))
plt.show()
plt.savefig('a.png')
hist(df[all_colums])
#绘制散点图
def scatter(df):
for i in all_colums[:6]:
plt.scatter(df[i],df['cnt'])
plt.xlabel(i)
plt.ylabel('cnt')
plt.show()
scatter(df)
#相关系数查看特征与特征,特征与响应的线性关系
def corr_view():
data_corr=df.corr()
data_corr=data_corr.abs()
sns.heatmap(data_corr,annot=True)
plt.savefig('b.png')
corr_view()
#异常值可视化
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
for i in all_colums:
f,ax=plt.subplots(figsize=(10,8))
sns.boxplot(y=i,data=df,ax=ax)
plt.show()
plt.savefig('c.png', dpi=500)
#经发现,'hum','windspeed','casual'这三列中有异常值
#异常值处理
# 通过Z-Score方法判断异常值,阙值设置为正负2
# 复制一个用来存储Z-score得分的数据框,常用于原始对象和复制对象同时进行操作的场景
df_zscore = df.copy()
for col in all_colums:
df_col = df[col]
z_score = (df_col - df_col.mean()) / df_col.std() # 计算每列的Z-score得分
df_zscore[col] = z_score.abs() > 2 # 判断Z-score得分绝对值是否大于2,大于2即为异常值
print(df_zscore)#显示为True的表示为异常值
# 剔除异常值所在的行
print(df[df_zscore['hum'] == False])
print(df[df_zscore['windspeed'] == False])
print(df[df_zscore['casual'] == False])#最终得到679x7的数列
#将清洗后的数据写入新的文件,命名为new_df
new_df=df[df_zscore['casual'] == False]
new_df.to_csv('new_df.csv')
#特征选择
#这里选择基于Filter(过滤法)中的卡方检验
from sklearn.feature_selection import chi2, SelectKBest
feutures=['temp','atemp','hum','windspeed','casual','registered']
X, y = new_df[feutures],new_df['cnt']
chi2_model = SelectKBest(chi2, k=3)
# 以下方法返回选择后的特征矩阵
chi2_model.fit_transform(X, y)
for i in range(X.shape[1]):
print((chi2_model.scores_[i], chi2_model.pvalues_[i]))
#可以发现,'casual','registered'这两个特征与目标'cnt'关系密切
final_df=new_df.loc[:,['casual','registered','cnt']]
final_df.to_csv('final_df.csv')
#再将最终有效数据放入新文件final_df中
#归一化;归一化通常有两种:最值归一化和均值方差归一化,这里采用均值方差归一化
from sklearn import preprocessing
from sklearn.preprocessing import StandardScaler
scaler=preprocessing.StandardScaler().fit(final_df)
final_df_scaler=scaler.transform(final_df)
print(final_df_scaler)
print(final_df_scaler.shape)
#(679, 3)
#对新文件训练集与测试集划分
from sklearn.model_selection import train_test_split
#random_state:设置随机种子,保证每次运行生成相同的随机数
train_set,test_set = train_test_split(final_df_scaler, test_size=0.2, random_state=42)
x_train=train_set[:,0:2]
y_train=train_set[:,2]
x_test=test_set[:,0:2]
y_test=test_set[:,2]
print(x_train.shape)
print(y_test.shape)
print(y_train.dtype)
#进行模型训练
#1.线性回归
from sklearn import linear_model
#from sklearn import model_selection
from sklearn.linear_model import LinearRegression
def test_LinearRegression():
linearRegression = linear_model.LinearRegression()
#进行训练
linearRegression.fit(x_train, y_train)
#通过LinearRegression的coef_属性获得权重向量,intercept_获得b的值
print("权重向量:%s, b的值为:%.2f" % (linearRegression.coef_, linearRegression.intercept_))
#计算出损失函数的值
print("损失函数的值: %.2f" % np.mean((linearRegression.predict(x_test) - y_test) ** 2))
#计算预测性能得分
print("预测性能得分: %.2f" % linearRegression.score(x_test, y_test))
test_LinearRegression()
#权重向量:[0.26697613 0.85123791], b的值为:-0.00
#损失函数的值: 0.00
#预测性能得分: 1.00
#2.使用非线性支持向量机(SVM)进行回归预测
from sklearn.svm import SVC
from sklearn import metrics
svm_model=SVC()#SVM分类器
svm_model.fit(x_train.astype("int"),y_train.astype("int"))#注:需要将数据类型转化为int型
prediction=svm_model.predict(x_test.astype("int"))
print('准确率为:',metrics.accuracy_score(prediction, y_test.astype("int")))
#准确率为: 0.9191176470588235文章出处登录后可见!
已经登录?立即刷新
