文章目录
1. DWA(Dynamic window approach)
动态窗口法(DWA)主要是在速度空间中采样多组速度,并模拟机器人在这些速度下一定时间内的轨迹。在得到多组轨迹以后,对这些轨迹进行评价,选取最优轨迹所对应的速度来驱动机器人运动。
1.1 机器人运动模型
动态窗口法将移动机器人的位置控制转换为速度控制。在利用速度模式对机器人运动轨迹进行预测时,首先需要对机器人的运动模型进行分析[1]。移动机器人采用的是两轮差速模型,分别代表机器人在世界坐标系下的平移速度与角速度,反映了机器人的运动轨迹。在机器人的编码器采样周期
内,位移较小,机器人作匀速直线运动,则机器人运动模型为:
式中
———t时刻机器人在世界坐标下的位姿。
1.2 速度采样
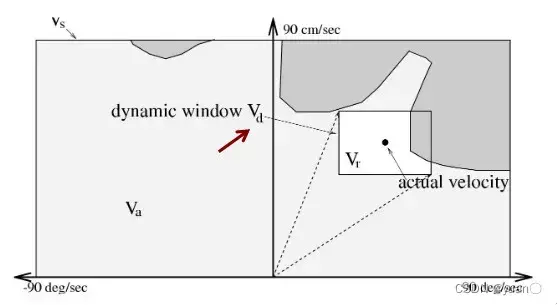
动态窗口法将避障问题描述为速度空间中带约束的优化问题,其中约束主要包括差速机器人的非完整约束、环境障碍物的约束以及机器人结构的动力学约束。DWA算法的速度矢量空间示意图如图1-1所示,横坐标为机器人角速度,纵坐标为机器人线速度
,其中
、
为机器人最大、最小线速度,
、
为机器人最大、最小角速度;整个区域为
,所有白色区域
为机器人安全区域,
为考虑电机扭矩在控制周期内限制的机器人可达速度范围,
为上述3个集合的交集最终确定的动态窗口。
根据机器人的速度限制,定义Vs为机器人线速度与角速度的集合,即动态窗口算法搜索求解的最大范围,满足:
式中
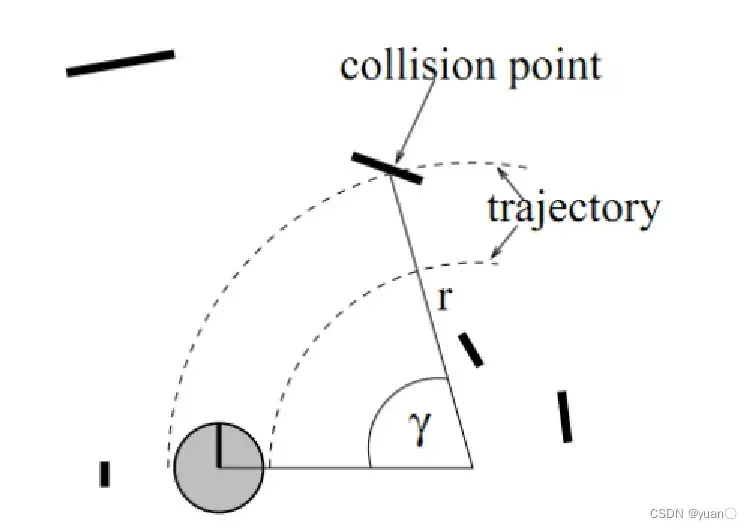
整个机器人的运动轨迹,可以细分为若干个直线或圆弧运动,为保证机器人安全区域,在最大减速度条件下,当前速度应能在撞击障碍物之前减速为0,则定义机器人碰撞可行区域的线速度与角速度集合
文章出处登录后可见!
已经登录?立即刷新
