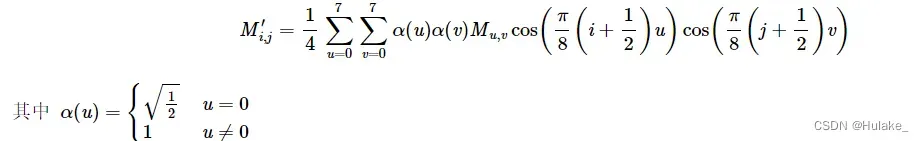想查看其他题的真题及题解的同学可以前往查看:CCF-CSP真题附题解大全
| 试题编号: | 202212-3 |
| 试题名称: | JPEG 解码 |
| 时间限制: | 1.0s |
| 内存限制: | 512.0MB |
| 问题描述: |
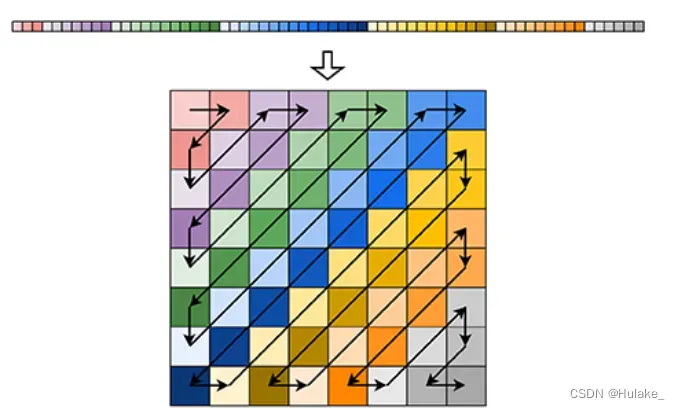
问题背景四年一度的世界杯即将画上尾声。在本次的世界杯比赛中,视频助理裁判(Video Assistant Referee, VAR)的应用可谓是大放异彩。VAR 使用视频回放技术帮助主裁判作出正确判罚决定。西西艾弗岛足球联赛的赛场上也引入了一套 VAR 设备。作为技术供应商的技术主管小C,需要存储和编码 VAR 产生的图像数据。小 C 分析比较发现,JPEG 编码算法可以达到较好的压缩效果,并且质量损失是可以接受的。因此,小 C 决定使用 JPEG 编码算法来存储和传输图像数据。JPEG 是一种常用的图片有损压缩算法,它的压缩率高,但是压缩后的图片质量下降较多。JPEG 图片的压缩率一般在 10:1 到 20:1 之间,一般用于存储照片等图片质量要求不高的场景。 为了简化问题,我们以灰度图片为例,介绍 JPEG 编码算法的过程。一张灰度图片,可以被视为由多个像素点组成。每个像素点对应一个 0 到 255 之间的数值,用于表示像素点的亮度。JPEG 编码算法将图片分割为 8×8 的小块,每个小块被称作一个最小编码单元。对每个小块进行如下的计算:
最后,将得到的各个小块的扫描数据采用哈夫曼编码进行压缩,并置于必要的数据结构中,就能得到一张 JPEG 图片了。 问题描述在本题中,你需要实现一个能够解码 JPEG 图片的一个最小编码单元的程序。解码的步骤与上述编码的步骤相反,具体的步骤是:
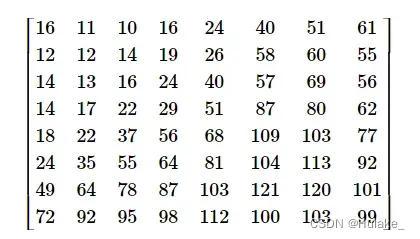
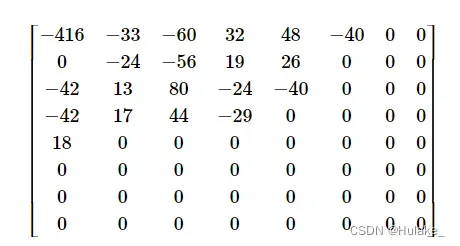
输入格式从标准输入读入数据。 输入的前 8 行,每行有空格分隔 8 个正整数,是量化矩阵。 接下来的 1 行是 1 个正整数 n,表示扫描数据的个数。 接下来的 1 行是 1 个数字 T,取值为 0、1 或 2,表示要进行的任务。 接下来的 1 行,有空格分隔的 n 个整数,是扫描数据。 输出格式输出到标准输出中。 输出共 8 行,每行有 8 个空格分隔的整数,表示一个图像矩阵。 当 T 取 0 时,输出填充(步骤 3)后的图像矩阵;当 T 取 1 时,输出量化(步骤 4)后的图像矩阵;当 T 取 2 时,输出最终的解码结果。 样例输入16 11 10 16 24 40 51 61 样例输出62 65 57 60 72 63 60 82 样例说明
子任务对于 20% 的数据,有 T=0; 对于 40% 的数据,有 T=0 或 1; 对于 100% 的数据,有 T∈{0,1,2},且 n∈[0,64],并且量化矩阵中的各个元素 qi,j 满足 0<qi,j<256,扫描序列中的各个元素 mi 满足 −256<mi<256。 提示在 C/C++ 语言中,可以通过包含 在 Python 语言中,可以通过 在 Java 语言中,可以使用 |
真题来源:JPEG 解码
感兴趣的同学可以如此编码进去进行练习提交
python题解:
c++满分题解:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 8;
int n, T;
int a[N][N], M[N][N], M1[N][N];
double M2[N][N];
int q[64];
double trans(double i, double j)
{
double res = 0;
for (int u = 0; u <= 7; u ++ )
for (int v = 0; v <= 7; v ++ )
if (u == 0 && v == 0)
res += (double)M1[u][v] * cos(0) * cos(0) / 2.0;
else if (u == 0)
res += (double)M1[u][v] * sqrt(0.5) * cos(acos(-1) * (i + 0.5) * double(u) / 8.0) * cos(acos(-1) * (j + 0.5) * v / 8.0);
else if (v == 0)
res += (double)M1[u][v] * sqrt(0.5) * cos(acos(-1) * (i + 0.5) * double(u) / 8.0) * cos(acos(-1) * (j + 0.5) * v / 8.0);
else
res += (double)M1[u][v] * cos(acos(-1) * (i + 0.5) * double(u) / 8) * cos(acos(-1) * (j + 0.5) * double(v) / 8.0);
return (double)res / 4.0;
}
int main()
{
for (int i = 0; i < 8; i ++ )
for (int j = 0; j < 8; j ++ )
cin >> a[i][j];
cin >> n >> T;
for (int i = 0; i < n; i ++ )
cin >> q[i];
// T1.
int k = 0;
for (int i = 0; i < 8; i ++ )
if (i % 2 == 0)
{
for (int j = 0; j <= i; j ++ )
M[i - j][j] = q[k ++ ];
}
else
for (int j = 0; j <= i; j ++ )
M[j][i - j] = q[k ++ ];
for (int i = 8; i < 15; i ++ )
if (i % 2 == 0)
for (int j = i - 7; j <= 7; j ++ )
M[i - j][j] = q[k ++ ];
else
for (int j = i - 7; j <= 7; j ++ )
M[j][i - j] = q[k ++ ];
// T2.
for (int i = 0; i < 8; i ++ )
for (int j = 0; j < 8; j ++ )
M1[i][j] = M[i][j] * a[i][j];
// T3.
for (int i = 0; i < 8; i ++ )
for (int j = 0; j < 8; j ++ )
{
M2[i][j] = round(trans(i, j) + 128);
if (M2[i][j] > 255) M2[i][j] = 255;
if (M2[i][j] < 0) M2[i][j] = 0;
}
// 输出
if (T == 0)
for (int i = 0; i < 8; i ++ )
{
for (int j = 0; j < 8; j ++ )
cout << M[i][j] << " ";
cout << endl;
}
if (T == 1)
for (int i = 0; i < 8; i ++ )
{
for (int j = 0; j < 8; j ++ )
cout << M1[i][j] << " ";
cout << endl;
}
if (T == 2)
for (int i = 0; i < 8; i ++ )
{
for (int j = 0; j < 8; j ++ )
cout << M2[i][j] << " ";
cout << endl;
}
return 0;
}
运行结果: 
借鉴: ShowerSong
文章出处登录后可见!