T 3.1
考虑文法
(a) 建立句子 和
的分析树。
见下面两题。
(b) 为 (a) 的两个句子构造最左推导。
最左推导的分析树(包括推导过程中的分析树):
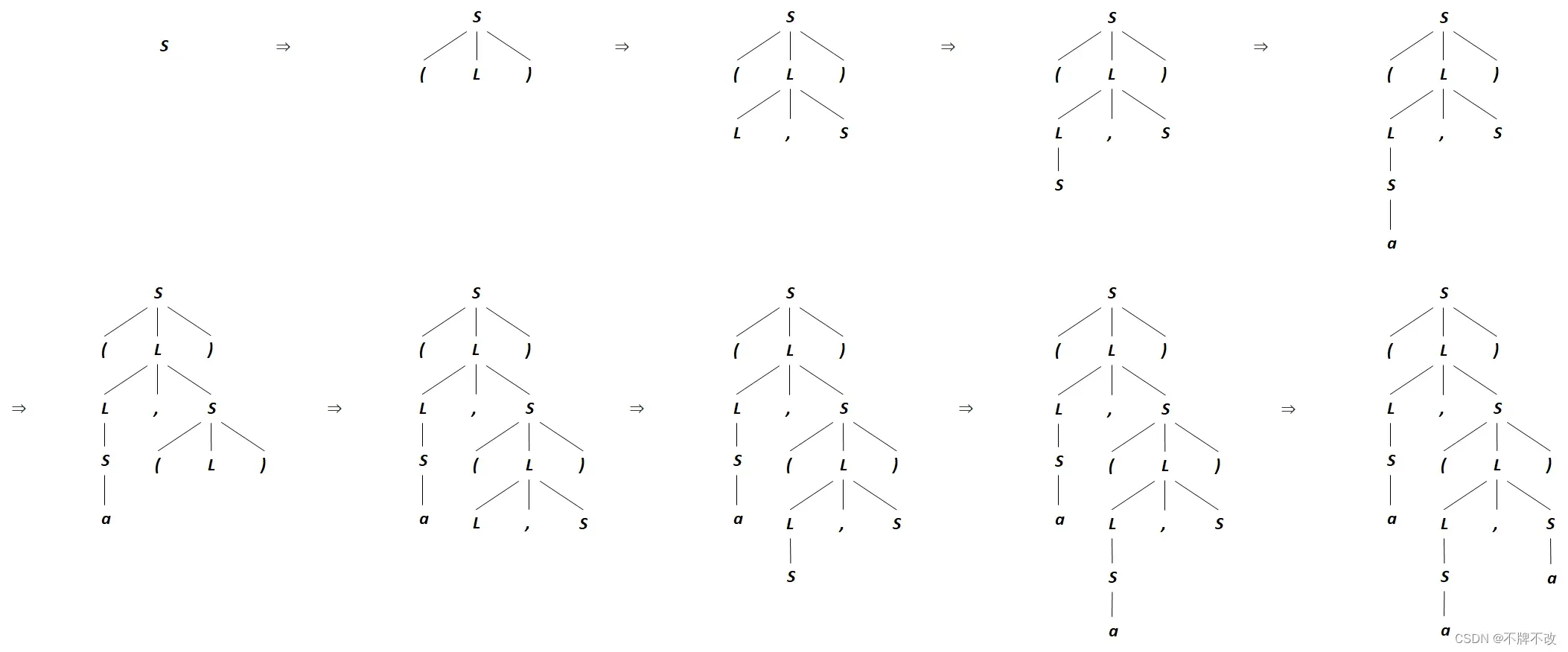
最左推导的分析树:
(c) 为 (a) 的两个句子构造最右推导。
最右推导的分析树(包括推导过程中的分析树):
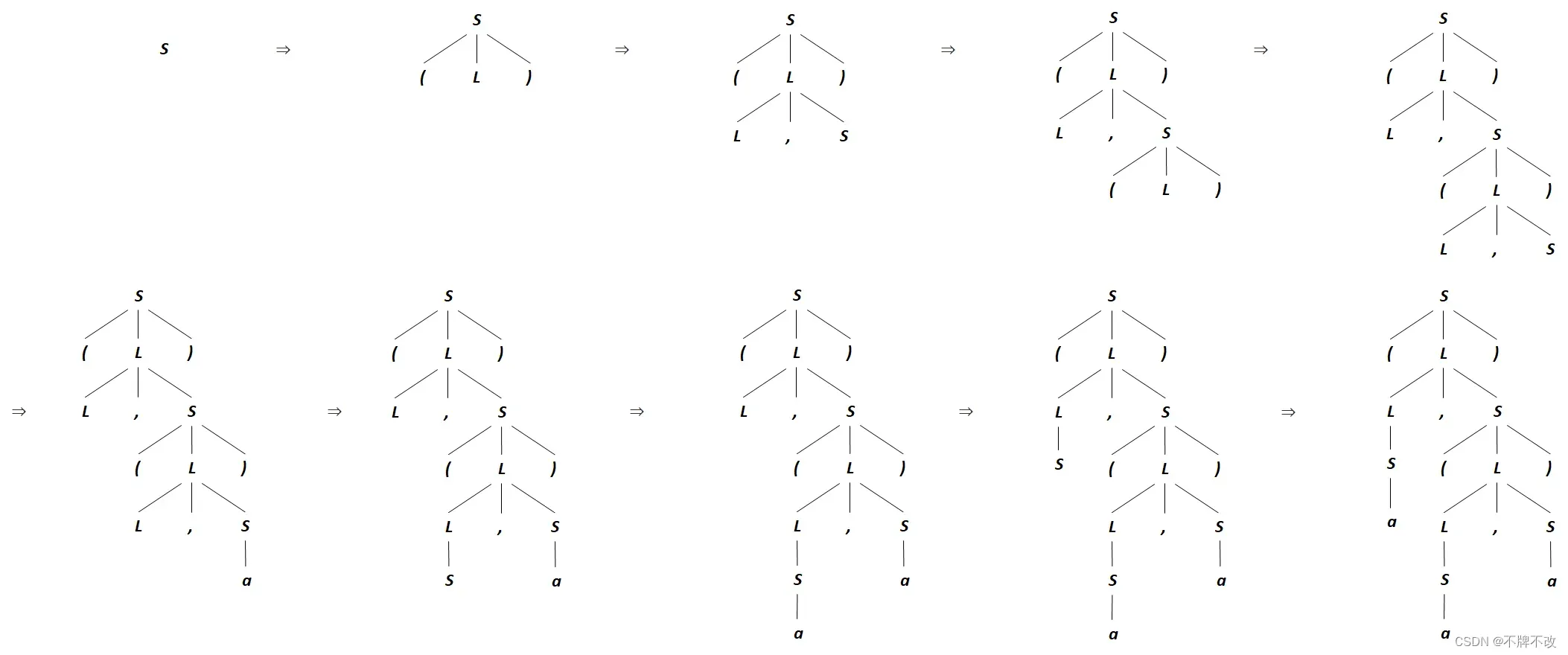
最右推导:
(d) 这个文法产生的语言是什么?
该文法产生的语言是括号匹配的串,串中的各项用“,”隔开,项可以是括号匹配的子串或 a。
T 3.2
考虑文法
(a) 为句子 构造两个不同的最左推导,以此说明该文法是二义的。
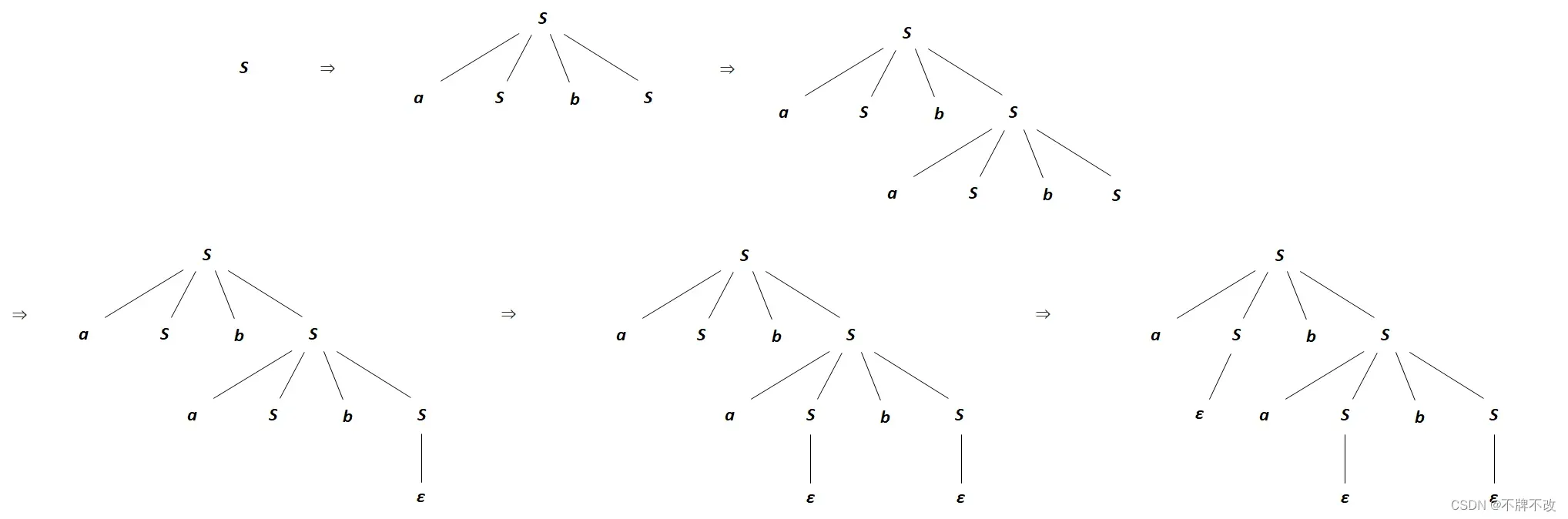
第一种最左推导的分析树(包括推导过程中的分析树):
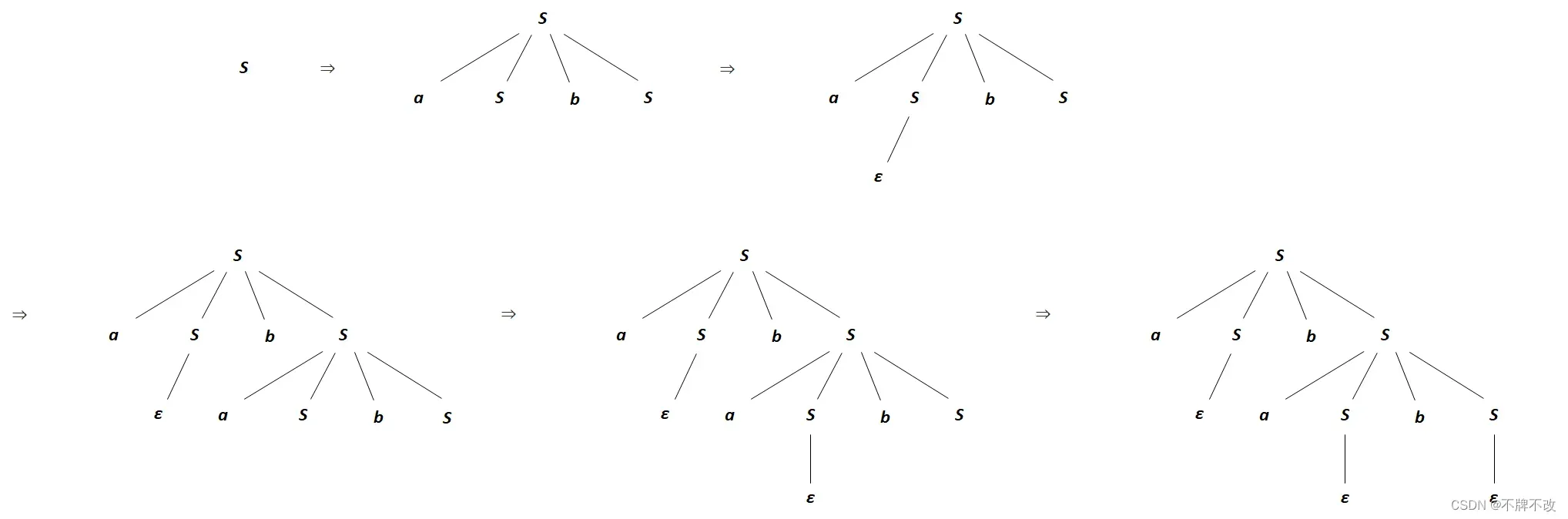
第二种最左推导的分析树(包括推导过程中的分析树):
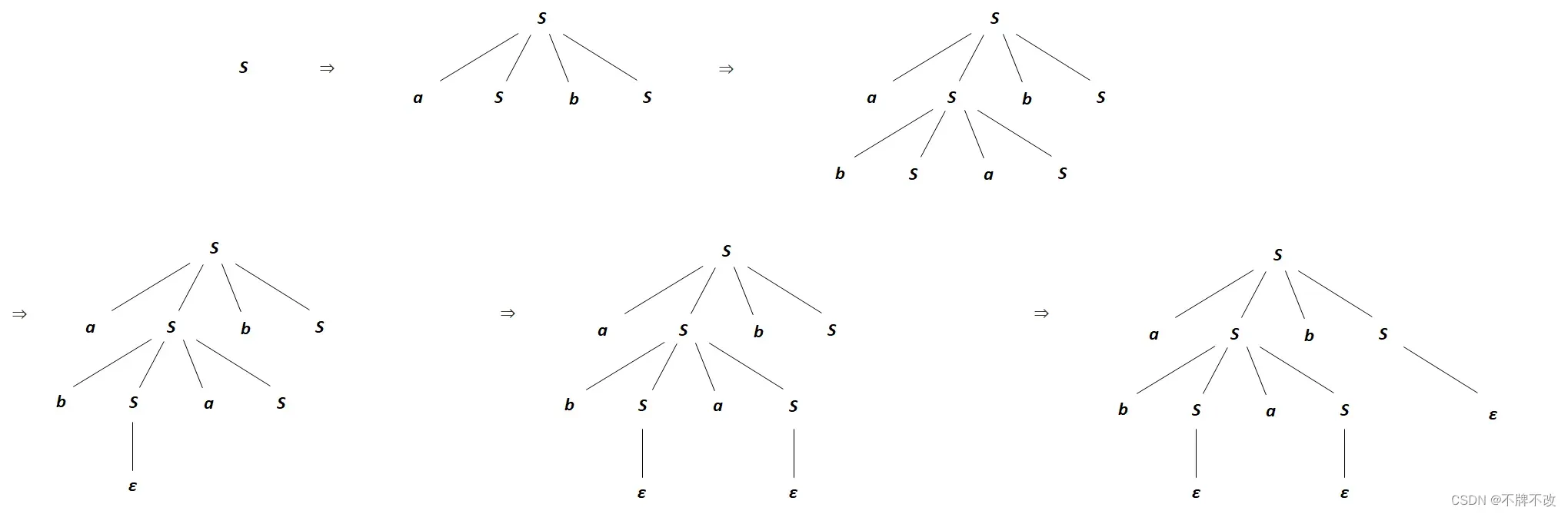
一个文法,如果存在某个句子有不止一棵分析树与之对应,那么称这个文法是二义的;故,该文法是是二义的。
(b) 为 构造对应的最右推导。
两种最右推导的分析树(包括推导过程中的分析树)如下:
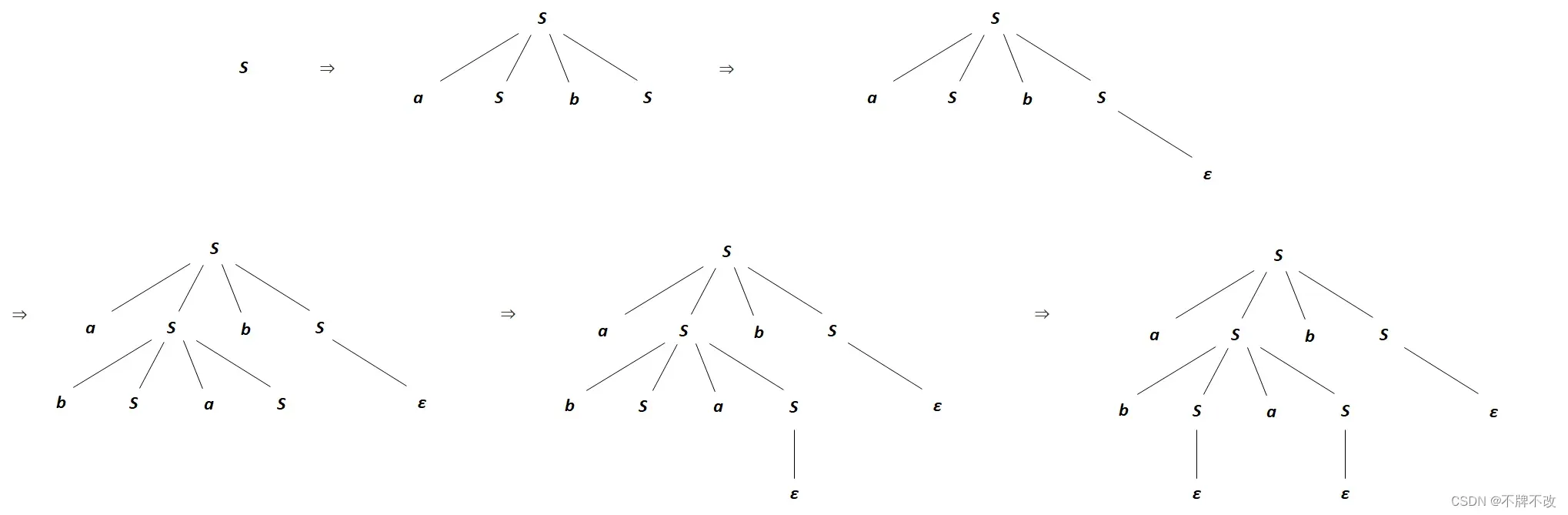
(c) 为 构造对应的分析树。
见上面四幅图。
(d) 这个文法产生的语言是什么?
通过最左推导的方式和产生式 可以得到前缀为若干个
的任意长度的串;
通过最左推导的方式和产生式 可以得到前缀为若干个
的任意长度的串;
题目给的产生式为 、
和
,由
可以推导出空串,可以说明可以产生
和
,因此由任意长度的前缀
和前缀
的子串可以构成
和
任意交错的串;
又因为每个产生式中 和
的个数都相同,故产生
和
数目相等且任意长度的串。
T 3.3
下面的二义文法描述命题演算公式,为它写一个等价的非二义性文法。
通过引入非终结符消除二义性:
T 3.4
文法
产生字母表 上所有不含
的正规式。注意,第一条竖线加了引号,它是正规式的或运算符号,而不是文法产生式右部各选择之间的分隔符,另外
在这里是一个普通的终结符。该文法是二义的。
(a) 证明该文法产生字母表 上的所有正规式。
证明:
(1) 该文法产生的串是字母表 上的正规式:
和
产生
和
,而
和
是
上的符号,因此是正规式。若
,
产生正规式
和
则:
产生正规式
产生正规式
产生正规式
产生正规式
(2) 字母表 上的所有正规式都可由此文法产生:
字母表 上的任一正规式(其中
,
为正规式)必为以下形式之一:
,可由
产生
,可由
产生
,可由
产生
,可由
产生
,可由
产生
,可由
产生
因而,该文法产生字母表 上的所有正规式
(b) 为该文法写一个等价的非二义文法。它给予算符 、连接和
的优先级和结合性同 2.2 节中定义的一致。
该文法没有体现运算符 、
、
和连接的优先级,因而是二义的。例如:
通过引入非终结符消除二义性:
消除二义性后:
(c) 按上面两个文法构造句子 的分析树。
存在二义性:
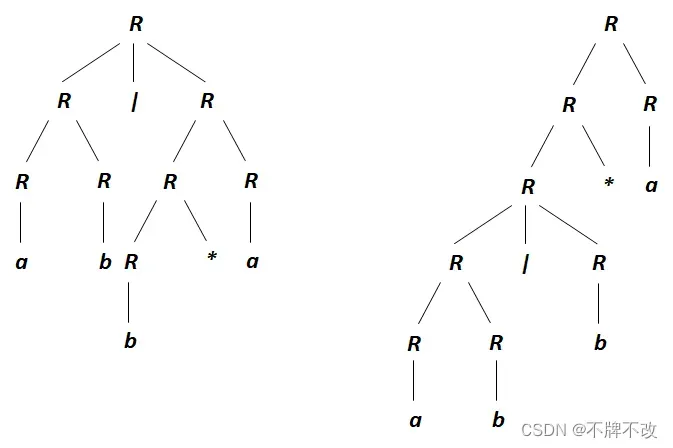
不存在二义性:
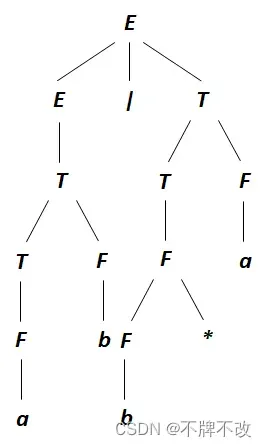
T 3.5
条件语句文法
试图消除悬空 的二义性,请证明该文法仍然是二义的。
由于不能保证
和
的配对,因而存在二义性。
句型 存在两个不同的最左推导。
期望的是:
if expr then
if expr then
matched_stmt
else
if expr then
matched_stmt
else
stmt
一种和期望不一样的推导:
stmt
=> matched_stmt
=> if expr then matched_stmt else stmt
=> if expr then if expr then matched_stmt else stmt else stmt
=> if expr then if expr then matched_stmt else if expr then stmt else stmt
=> if expr then if expr then matched_stmt else if expr then matched_stmt else stmt
if expr then
if expr then
matched_stmt
else
if expr then
matched_stmt
else
stmt
另一种推导:
stmt
=> if expr then stmt
=> if expr then matched_stmt
=> if expr then if expr then matched_stmt else stmt
=> if expr then if expr then matched_stmt else matched_stmt
=> if expr then if expr then matched_stmt else if expr then matched_stmt else stmt
if expr then
if expr then
matched_stmt
else
if expr then
matched_stmt
else
stmt
T 3.8
(a) 消除习题 3.1 文法的左递归。
(b) 为 (a) 的文法构造预测分析器。
| 非终结符 | 输入符号 | ||||
| ( | ) | a | , | $ | |
| S | S→(L) | S→a | |||
| L | L→SL’ | L→SL’ | |||
| L’ | L’→ε | L→,SL’ | L’→ε | ||
T 3.10
构造下面文法的 LL(1) 分析表。
先确定非终结符的 和
集:
| 非终结符 | 输入符号 | ||||
| int | real | id | , | $ | |
| D | D→TL | D→TL | |||
| T | T→int | T→real | |||
| L | L→idR | ||||
| R | R→,idR | R→ε | |||
T 3.11
构造下面文法的 LL(1) 分析表。
| 非终结符 | 输入符号 | ||
| a | b | $ | |
| S | S→aBS S→ε | S→bAS S→ε | S→ε |
| A | A→a | A→bAA | |
| B | B→aBB | B→b | |
T 3.12
下面的文法是否为 LL(1) 文法,说明理由。
上面文法不是 LL(1) 文法。
LL(1) 文法:对于产生式 满足:
①
② 若 ,那么
而本题中,,
,不满足条件 ①,故,上面文法不是 LL(1) 文法。
T 3.18
为习题3.3的文法构造SLR分析表
扩展文法:


| action | goto | ||||||||
| and | or | not | true | false | ( | ) | $ | S | |
| 0 | s2 | s3 | s4 | s5 | 1 | ||||
| 1 | s6 | s7 | acc | ||||||
| 2 | s2 | s3 | s4 | s5 | 8 | ||||
| 3 | r4 | r4 | r4 | r4 | |||||
| 4 | r5 | r5 | r5 | r5 | |||||
| 5 | s2 | s3 | s4 | s5 | 9 | ||||
| 6 | s2 | s3 | s4 | s5 | 10 | ||||
| 7 | s2 | s3 | s4 | s5 | 11 | ||||
| 8 | s6/r3 | s7/r3 | r3 | r3 | |||||
| 9 | s6 | s7 | r12 | ||||||
| 10 | s6/r1 | s7/r1 | r1 | r1 | |||||
| 11 | s6/r2 | s7/r2 | r2 | r2 | |||||
| 12 | r6 | r6 | r6 | r6 | |||||
T 3.29
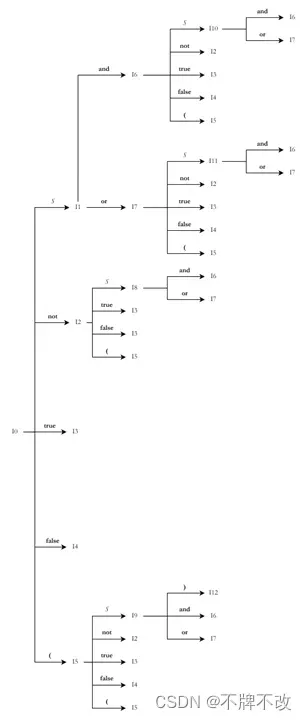
(a) 为下面文法构造规范LR(1)分析表,画出像图3.20这样的状态转换图就可以。
详述构建的过程:
① 拓展文法:
② 由于后面不会存在任何字符,所以其
集中只有$元素,因此产生式(0)的搜索符为$

③ 对于项目 $
,可以将产生式(1)代入,因为项目右部
后面为空串,所以新项目的搜索符为$,故得到新项目
$
;类似地,将产生式(2)代入,得到新项目
$

④ 对于项目 $,可以将产生式(3)和(4)代入,因为项目右部
后面为
,所以新项目的搜索符为
,而不是$,故得到新项目
和

⑤ 对于项目$,可以将产生式(5)代入,因为项目右部
后面为空串,所以新项目的搜索符为$,故得到新项目
$

⑥ 项目和
不会产生新的项目
⑦ 对于项目 $,可以将产生式(3)和(4)代入,注意此时产生的新项目应该继承项目
$的搜索符$,因此两个新项目为
$和
$

⑧ 不妨将第一个分量相同的项目对应的搜索符集合合并一下

生成其他状态的道理类似,只展示结果。

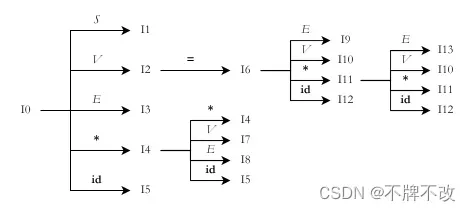
(b) 上述状态转换图有同心项目集吗?若有,合并同心项目集后是否会出现动作冲突?
其中和
、
和
、
和
、
和
分别为同心项目集。
同心项目集的合并(又得到LALR自动机的过程)不会引入新的移进-归约冲突,可能会引入新的归约-归约冲突;又因为规范LR(1)自动机已经解决了移进-归约冲突的问题,所以只需要验证是否存在归约-归约冲突即可。显然合并后不存在归约-归约冲突,综上,不存在动作冲突。
文章出处登录后可见!
