(To Learn More) ML Lecture 1: Regression – Case Study（下）

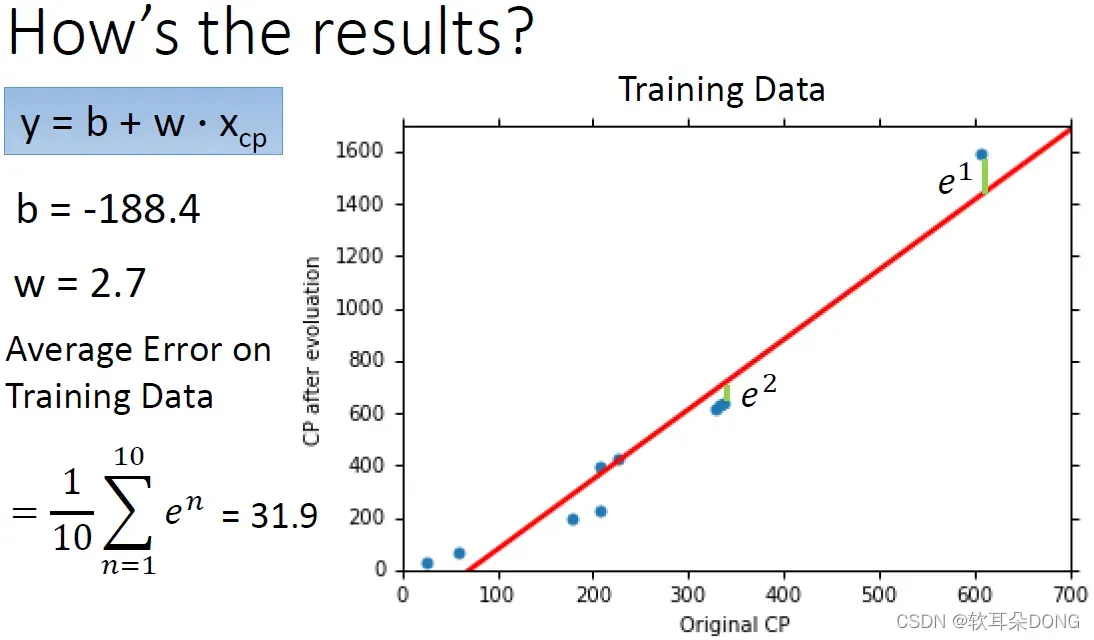
linear regression的函式根据training data找出来最好的b和w分别是b=-188.4和w=2.7。如果你把这一个，把它的b跟w值画到图上的话，它长的是这个样子，这一条红色的线。那你可以计算一下，你会发现说这一条红色的线，没有办法完全正确的评定所有的宝可梦的进化后的CP值。如果你想要知道说他做的有多不好的话，或者是多好的话，你可以看一下，你可以计算一下你的error。你的error就是计算一下每一个蓝色的点跟这个红色的点之间的距离，第一个蓝色的点跟这个红色的线的距离是，第二个蓝色的点跟红色的线的距离是，以此类推，所以有到。那平均的training data的error，就是summation到除以10：，这边算出来是31.9。

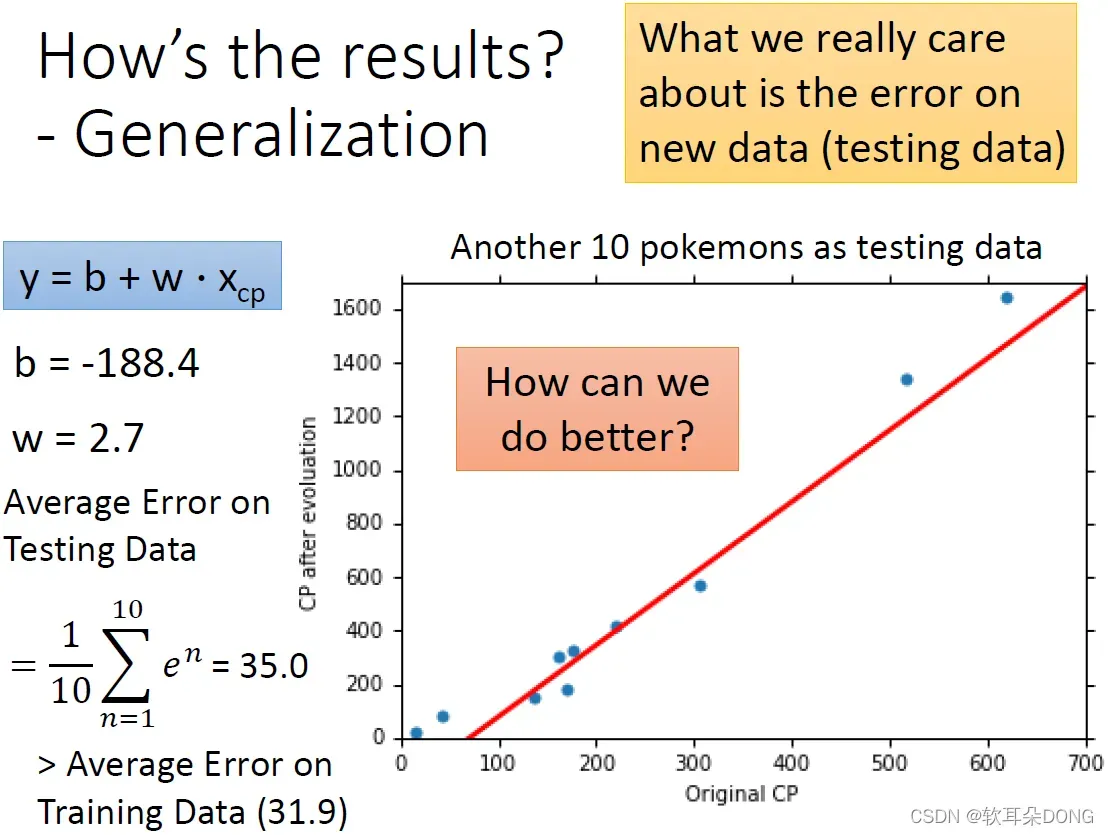
但是这个并不是我们真正关心的，因为你真正关心的是，generalization的case，也就是说，假设你今天抓到一只新的宝可梦以后，如果使用你现在的model去预测的话，那做出来你估测的误差到底有多少？所以真正关心的是，那些你没有看过的新的data，这边我们叫做testing data，它的误差是多少？所以这边又抓了另外10只宝可梦，当作testing data，这10只宝可梦跟之前拿来做训练的10只，不是同样的10只。其实这新抓的10只跟刚才看到的10只的分布，其实是还蛮像的，它们就是这个图上的10个点。那你会发现说，我们刚才在训练资料上找出来这条红色的线，其实也可以大致上预测，在我们没有看过的宝可梦上，它的进化后的CP值。如果你想要量化它的错误的话，那就计算一下它的错误，它错误算出来是35.0，这个值是比我们刚才在training data上看到的error还要稍微大一点，因为可以想想看我们最好的function是在training data上找到的，所以在training data上面算出来的error，本来就应该比testing data上面算出来的error还要稍微大一点。那有没有办法做得更好呢？如果你想要做得更好的话，接下来你要做的事情就是，重新去设计你的model，如果你观察一下data你会发现说，在原进化前的CP值特别大的地方，还有进化前的CP值特别小的地方，预测是比较不准的。那你可以想想看说，任天堂在做这个游戏的时候，它背后一定是有某一支程序，去根据某一些hidden的factor，比如说，根据原来的CP值和其他的一些数值generate进化以后的数值，所以到底它的function长甚么样子？从这个结果看来，那个function可能不是这样子一条直线，它可能是稍微更复杂一点。所以我们需要有一个更复杂的model。

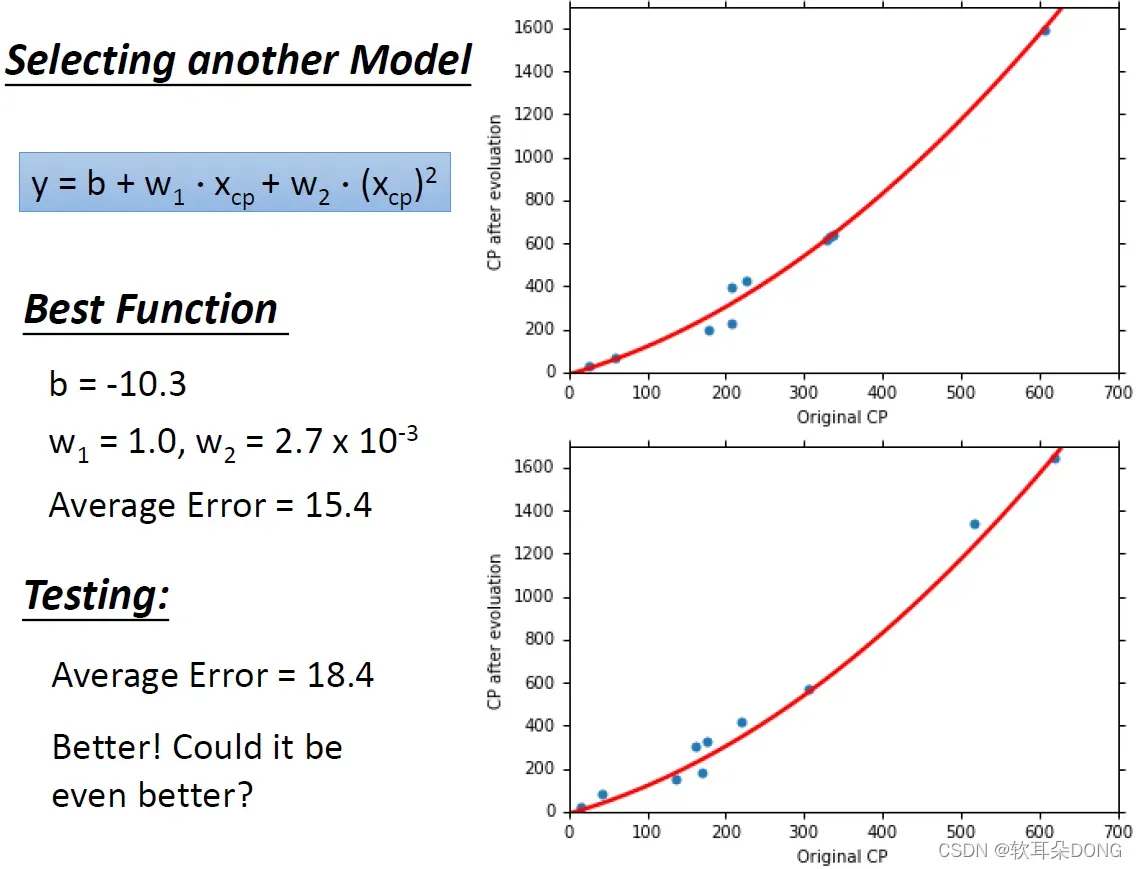
举例来说，我们这边可能需要引入二次式。我们今天可能需要引入这一项，我们重新设计了一个model，这个model它写成，我们加了后面这一项，如果我们有了这个新的function，你可以用我们刚才讲得一模一样的方式，去define一个function的好坏，然后用gradient descent，找出一个在你的function set里面最好的function。根据training data找出来的最好的function是，，。

如果我们把这个最好的function画在图上的话，你就会发现说，现在我们有了这条新的曲线，我们有了这个新的model，它的预测在training data上面看起来是更准一点，在training data上面你得到的average error现在是15.4。但我们真正关心的是testing data，那我们就把同样的model再apply到testing data上，我们在testing data上apply同样这条红色的线，然后去计算它的average error，那我们现在得到的是18.4。在刚才如果我们没有考虑的时候，算出来的average error是30左右，现在有考虑平方项得到的是18.4。

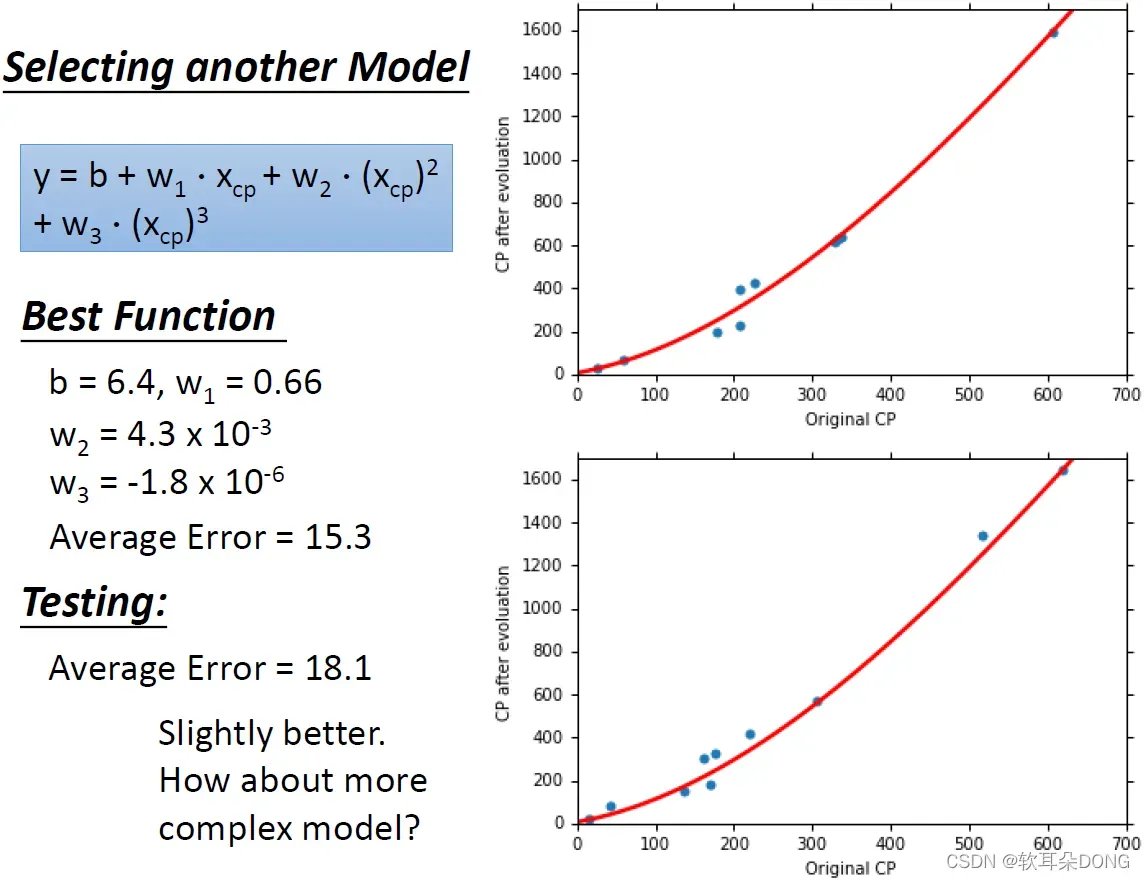
那有没有可能做得更好呢？比如说我们可以考虑一个更复杂的model，我们引入不只是，我们引入，所以我们现在的model长的是这个样子。你就用一模一样的方法，你就可以根据你的training data，找到在这一个function set里面，在这个model里面最好的一个function。那找出来是这样：，，，，所以你发现其实是它的值比较小，它可能是没有太大的影响，作出来的线其实跟刚才看到的二次的线是没有太大的差别的，那做出来看起来像是这个样子，那这个时候average error算出来是15.3。如果你看testing data的话，testing data算出来的average error是18.1，跟刚刚二次的，有考虑的结果比起来是稍微好一点点，刚才前一页是18.3，有考虑三次项后是18.1，是稍微好一点点。

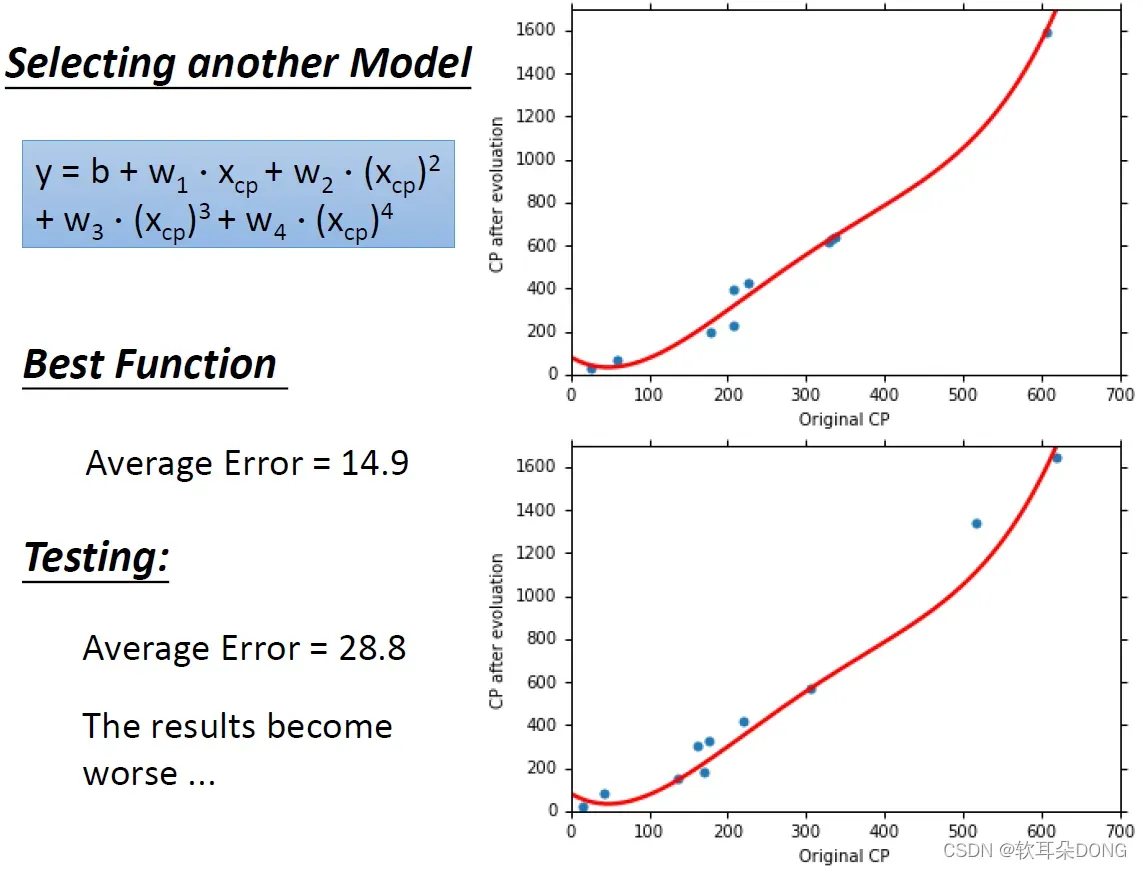
那有没有可能是更复杂的model呢？或许在宝可梦的那个程序背后，它产生进化后的CP值用的是一个更复杂的一个function，或许它不只考虑了三次，或者它不只考虑了，或许它考虑的是四次方也说不定，那你就用同样的方法，再把这些参数：、、、和都找出来，那你得到的function长这个样子。你发现它在training data上它显然可以做得更好，在input的CP值比较小的这些宝可梦，这些显然是一些绿毛虫之类的东西，它在这边是predict更准的。所以现在的average error是14.9，刚才三次的是15.3，刚才三次的是在training data上是15.3，现在四次的时候在training data上是14.9。但是我们真正关心的是testing，我们真正关心的是如果没有看过的宝可梦，我们能够多精确的预测它进化后的CP值。我们发现说，如果我们看没有看过的宝可梦的话，我们得到的average error是多少呢？我们得到的average error其实是28.8，前一页做出来已经是18.3了，就我们用三次的时候，在testing data上面做出来已经是18.3了，但是我们换了一个更复杂的model以后，做出来是28.8，结果竟然变得更糟了！我们换了一个更复杂的model，在training data上给我们比较好的结果，但在testing data上，看起来结果是更糟的。

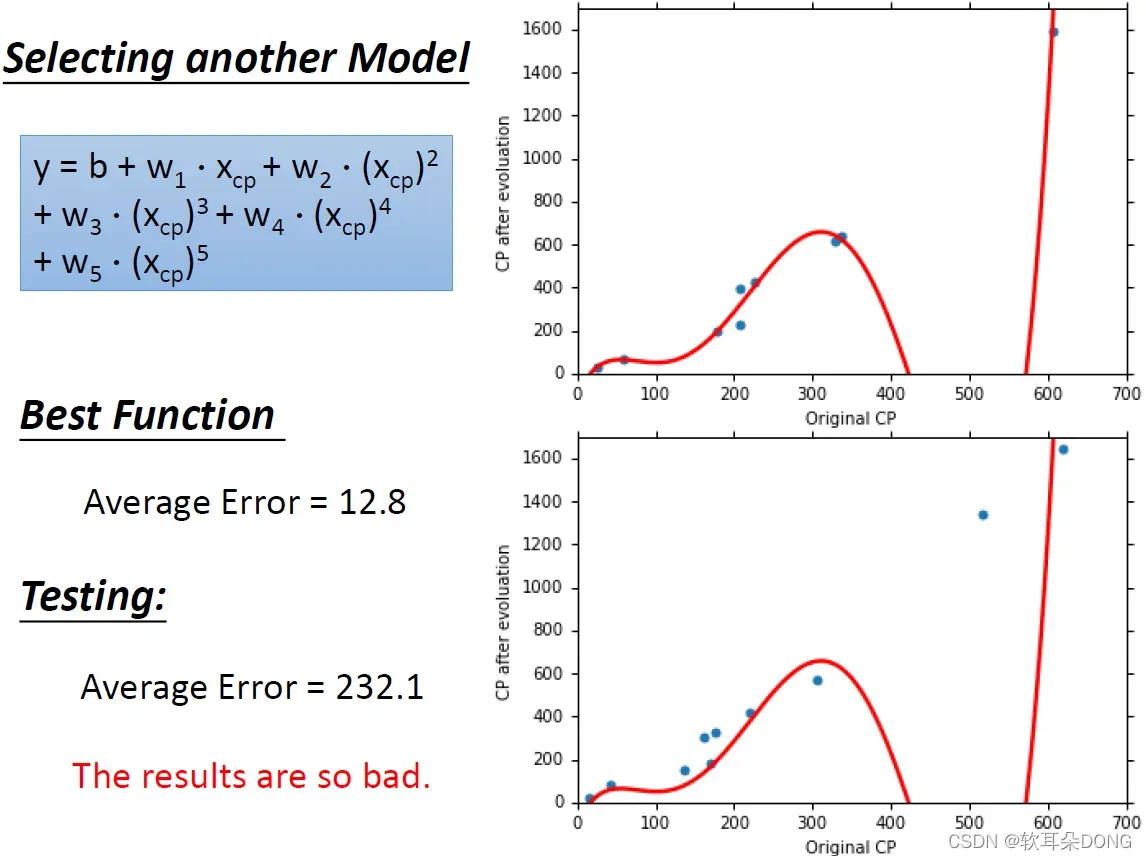
那如果换再更复杂的model会怎样呢？有没有可能是五次式，有没有可能它背后的程序是如此的复杂，它考虑了原来的CP值的一次、两次、三次、四次到五次。那这个时候，我们把最好的function找出来，你会发现它最好的function在training data上长得像是这样子，这个是一个合理的结果吗？你会发现说，在原来的CP值是500左右，500左右可能就是伊布之类的东西。在原来的CP值是500左右的宝可梦，根据你现在的model预测出来，它的CP值竟然是负的。但是在training data上面，我们可以算出来的error是12.8，比我们刚才用四次式，得到的结果又再更好一些。那在testing的结果上是怎样呢？如果我们把这个我们找出来的function，apply到新的宝可梦上面，你会发现结果怎么烂掉了啊，至少这一只大概是伊布吧，这只伊布，它预测出来进化后的CP值，是非常的不准，照理说有1000多，但是你的model却给它一个负的预测值，所以算出来的average error非常大，有200多，所以当我们换了一个更复杂的model，考虑到五次的时候，结果又更加糟糕了。

所以到目前为止，我们试了五个不同的model。那这五个model，如果你把他们分别的在training data上面的average error都画出来的话，你会得到这样子的一张图（右上）。从高到低，也就是说，如果你考虑一个最简单的model，这个时候error是比较高的；model稍微复杂一点，error稍微下降；然后model越复杂，在这个training data上的error就会越来越小。那为甚么会这样呢？这件事情倒是非常的直觉，非常容易解释。假设黄色的这个圈圈，我们故意用一样的颜色，黄色这个圈圈代表这一个式子，有考虑三次的式子所形成的function space。那四次的式子所形成的function space，就是这个绿色的圈圈。它是包含黄色的圈圈的。这个事情很合理，因为你只要把设为0，是四次的这个式子就可以变成三次的式子，所以三次的式子都包含在这个四次的式子里面，黄色的圈圈都包含在绿色的圈圈里面。那如果我们今天考虑更复杂的五次的式子的话，它又可以包含所有四次的式子。

所以今天如果你有一个越复杂的model，它包含了越多的function的话，那理论上你就可以找出一个function，它可以让你的error rate越来越低。你的function如果越复杂，你的candidate如果越多，你当然可以找到一个function，让你的error rate越来越低。当然这边的前提就是，你的gradient descent要能够真正帮你找出best function的前提下，你的function越复杂，可以让你的error rate在training data上越低。

但是在testing data上面，看起来的结果是不一样的。在training data上，你会发现说，model越来越复杂你的error越来越低，但是在testing data上，在到第三个式子为止，你的error是有下降的，但是到第四个和第五个的function的时候，error就暴增。然后把它的图试着画在左边这边。蓝色的是training data上对不同function的error，橙色的是testing data上对不同function的error。你会发现说，今天在五次的时候，在testing上是爆炸的，它就突破天际没办法画在这张图上。那所以我们今天得到一个观察，虽然说越复杂的model可以在training data上面给我们越好的结果，但这件事情也没有甚么，因为越复杂的model并不一定能够在testing data上给我们越好的结果。

这件事情就叫做，就复杂的model在training data上有好的结果，但在testing data上不一定有好的结果。比如当我们用第四个和第五个式子的时候，我们就发生overfitting的情形。那为甚么会有overfitting这个情形呢？为甚么更复杂的model它在training上面得到比较好的结果，在testing上面不一定得到比较好的结果呢？这个我们日后再解释。所以model不是越复杂越好，我们必须选一个刚刚好，没有非常复杂也没有很复杂的model，你要选一个最适合的model。比如说在这个case里面，当我们选一个三次式的时候，可以给我们最低的error。所以如果今天可以选的话，我们就应该选择三次的式子来作为我们的model，来作为我们的function set。

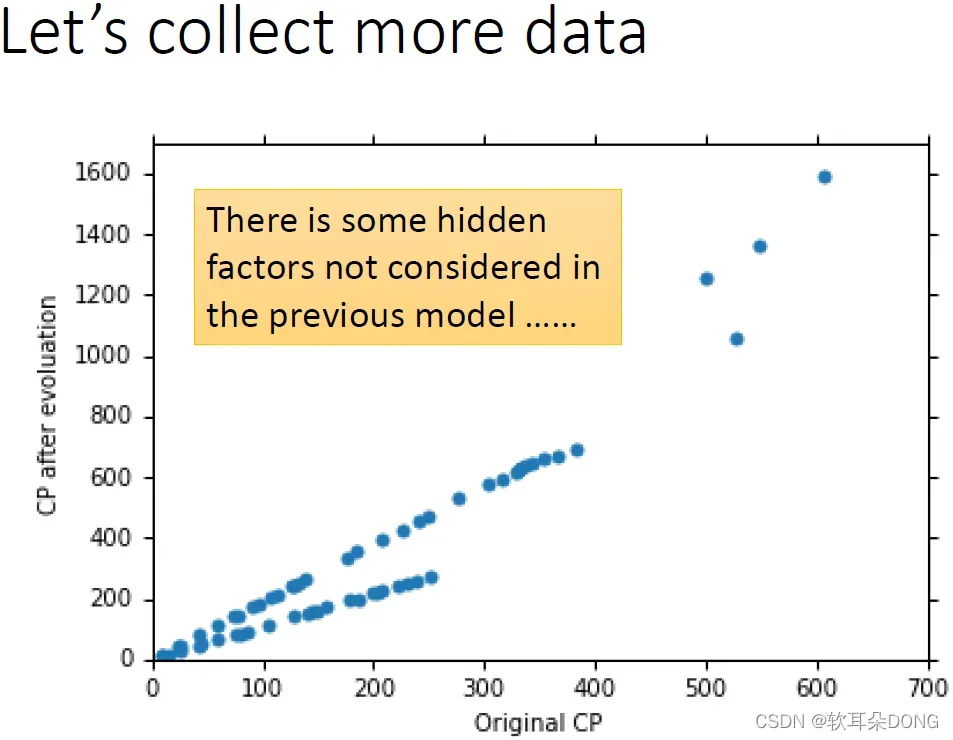
你以为这样就结束了吗？其实还没有，刚才只收集了10只宝可梦，其实太少了，当我们收集到60只宝可梦的时候，你会发现说刚才都是白忙一场。当我们收集60只宝可梦，你把它的原来的CP值和进化后的CP值，画在这个图上，你会发现说他们中间有一个非常奇妙的关系。它显然不是甚么一次二次三次一百次式，显然都不是，中间有另外一个力量，这个力量不是CP值它在影响着进化后的数值，到底是甚么呢？

其实非常的直觉，就是宝可梦的物种。这边我们把不同的物种用不同的颜色来表示，蓝色是波波，波波进化后是比比鸟，比比鸟进化是大比鸟。这个黄色的点是独角虫，独角虫进化后是铁壳蛹，铁壳蛹进化后是大针蜂。然后绿色的是绿毛虫，绿毛虫进化是铁甲蛹，铁甲蛹进化是巴大蝴。红色的是伊布，伊布可以进化成雷精灵、火精灵或水精灵等等。你可能说怎么都只有这些路边就可以见到的，因为抓乘龙快龙是很麻烦的，所以就只有这些而已。所以刚才只考虑CP值这件事，只考虑进化前的CP值显然是不对的。因为这个进化后的CP值受到物种的影响其实是很大的。

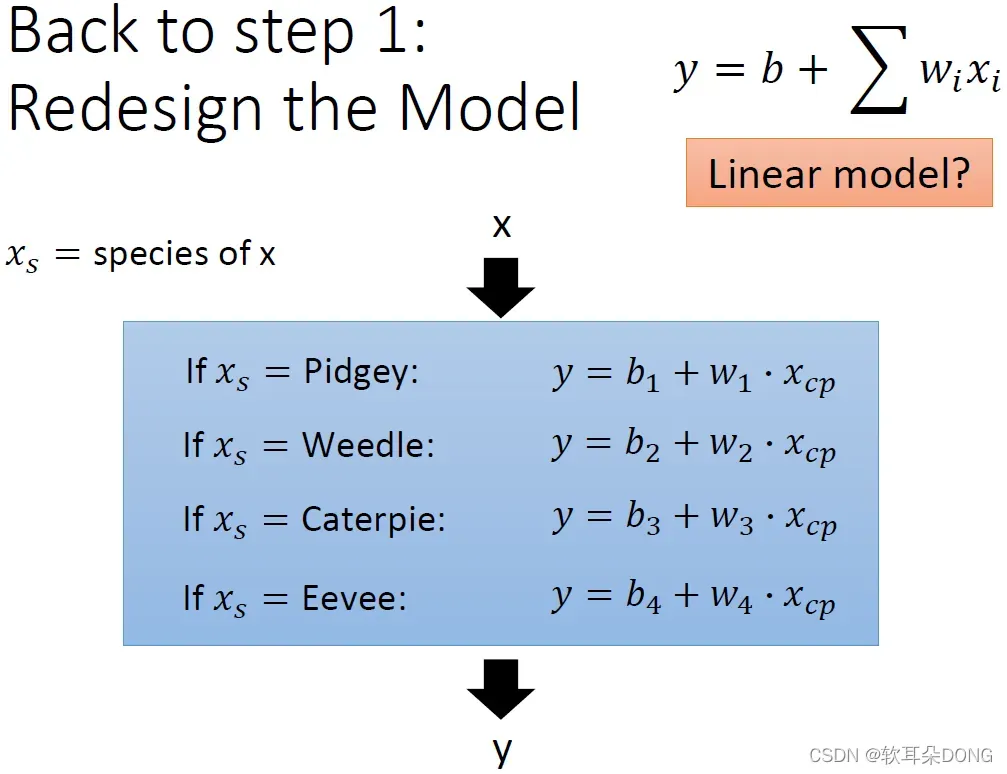
所以我们在设计model的时候，刚才那个model设计的是不好的，刚才那个model就好像是：你想要海底捞针，从function set里面捞出一个最好的model，那其实里面model通通都不好，所以针根本就不在海里。所以这边就重新设计一下function set，我们的function set，input x跟output y，这个input宝可梦和output进化后的CP值有甚么关系呢？它的关系是这样：如果今天输入的宝可梦x，它的物种是属于波波的话，这个代表说这个input x的物种，那他的输出。那如果它是独角虫的话，。如果它是绿毛虫的话，就是。如果它是伊布的话，就用另外一个式子。也就是不同的物种，我们就看它是哪一个物种，我们就代不同的linear function，然后得到不同的y作为最终的输出。你可能会问一个问题说，你把if放到整个function里面，这样你不就不是一个linear model了吗？这个function里面有if你搞得定吗？你可以用微分来做吗？你可以用刚才的gradient descent来算参数对loss function微分吗？其实是可以的。这个式子你可以把它改写成一个linear function。

写起来就是这样，这个有一点复杂但没有关系。我们先来观察一下δ这个function，如果你有修过信号的处理，我想应该知道δ这个function是指甚么？今天这个δ这个function的意思是说，的意思就是说：假如我们今天输入的这只宝可梦是波波的话，这个δ function它的output就是1。反之如果是其他种类的宝可梦的话，它δ function的output就是0。所以我们可以把刚才那个有if的式子，写成像这边这个样子：。

你可能会想说这个跟刚刚那个式子哪里一样了呢？你想想看，假如我们今天输入的那一只宝可梦是波波的话，假如等于波波（Pidgey）的话，意味着这两个function（）会是1，这两个δ function如果input是波波的话就是1，其他δ function就是0。那乘上0的项就当作没看到，其实就变成，所以对其他种类的宝可梦来说也是一样。所以当我们设计这个function的时候，我们就可以做到我们刚才在前一页design的那一个有if的function。那事实上这一个function，它就是一个linear function，怎么说呢？前面这个到就是我们的参数，而后面这一项δ或者是δ乘以就是feature，所以这个东西它也是linear model。

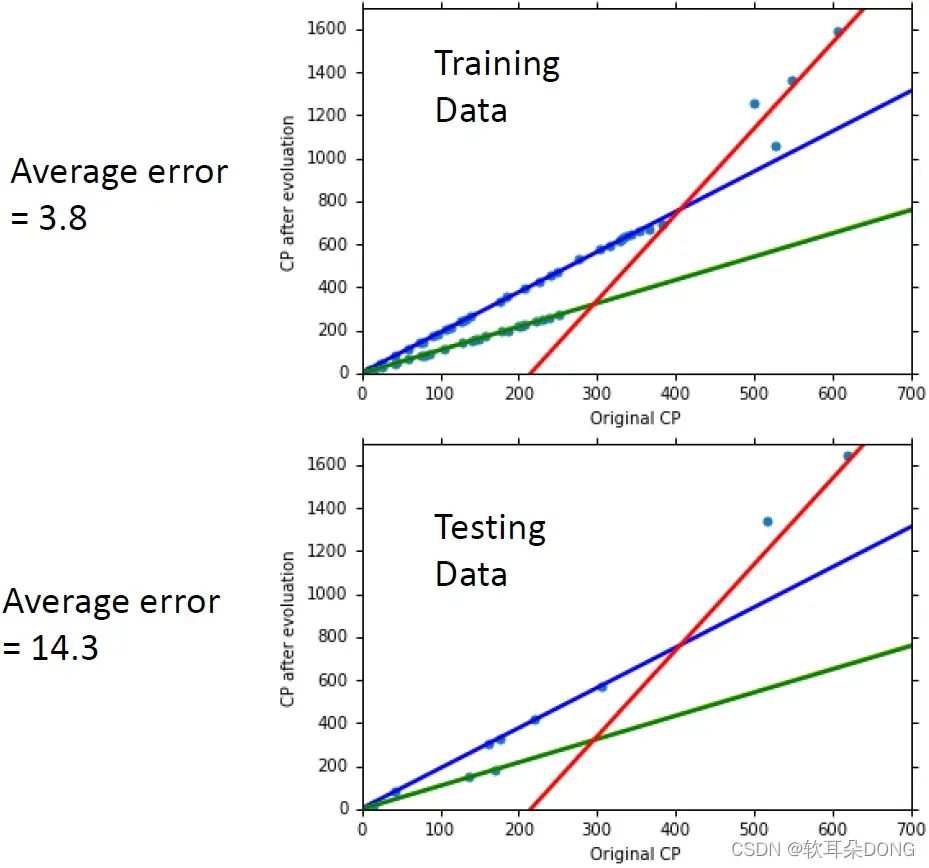
那有了这些以后，我们做出来的结果怎么样呢？这个是在training data上的结果，在training data上面，我们知道不同种类的宝可梦，它用的参数就不一样。所以不同种类的宝可梦，它的线是不一样的，它的model的那条line是不一样的。蓝色这条线是波波的线，绿色这条线是绿毛虫的线，黄色独角虫的线跟绿毛虫的线其实是重迭的，红色这条线是伊布的线。所以就发现说，当我们分不同种类的宝可梦来考虑的时候，我们的model在training data上面可以得到更低的error。你发现说现在这几条线，是把training data fit得更好，是把training data解释得更好，如果我们这么做有考虑到宝可梦的种类的时候，我们得到的average error是3.8在training data上。但我们真正在意的是，它能不能够预测新看到的宝可梦，也就是testing data上面的结果。那在testing data上面，它的结果是这个样子，一样是这三条线，发现说它也把在testing data上面的那些宝可梦fit得很好，然后它的average error是14.3，这比我们刚才可以做好的18点多还要更好。但是如果你再观察这个图的话，感觉应该是还有一些东西是没有做好的，我仔细想想看，我觉得伊布这边应该就没救了，因为我认为伊布会有很不一样的CP值是因为进化成不同种类的精灵，所以如果你没有考虑这个factor的话，应该就没救了。但是我觉得这边有一些还没有fit很好的地方，有一些值还是略高或略低于这条直线，所以这个地方搞不好还是有办法解释的。当然有一个可能是，这些略高略低于我们现在找出来这个蓝色绿色线的这个model的变化，这个difference其实来自于random的数值，就是每次那个宝可梦的程序产生进化后的CP值的时候，它其实有加一个random的参数。

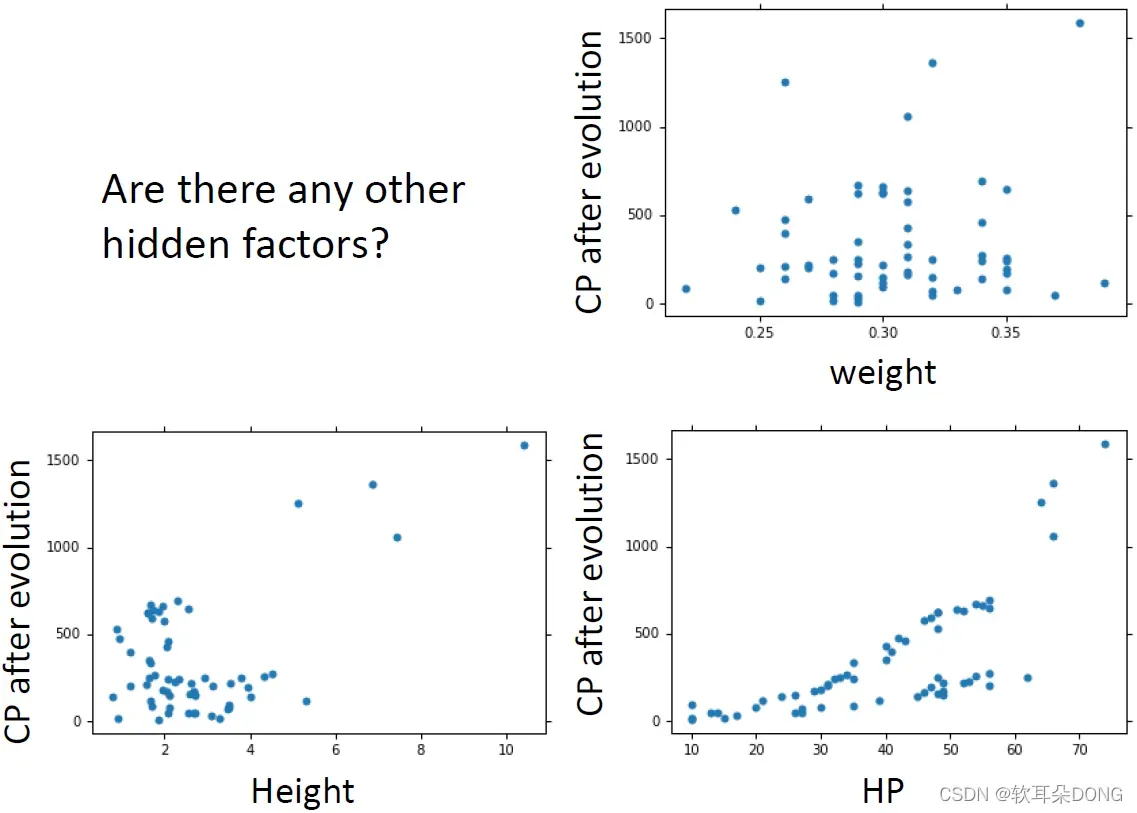
但也有可能是其实不是random的参数，它还有其他的东西在影响着宝可梦进化后的CP值。有什么其他可能的参数呢？会不会进化后的CP值是跟weight有关系的？会不会进化后的CP值是跟它的高度（Height）有关系的？会不会进化后的CP值是跟它的HP有关系的？其实我们不知道，我又不是大木博士我怎么会知道这些事情。如果你有domain knowledge的话，你就可能可以知道说，你应该把甚么样的东西，加到你的model里面去。

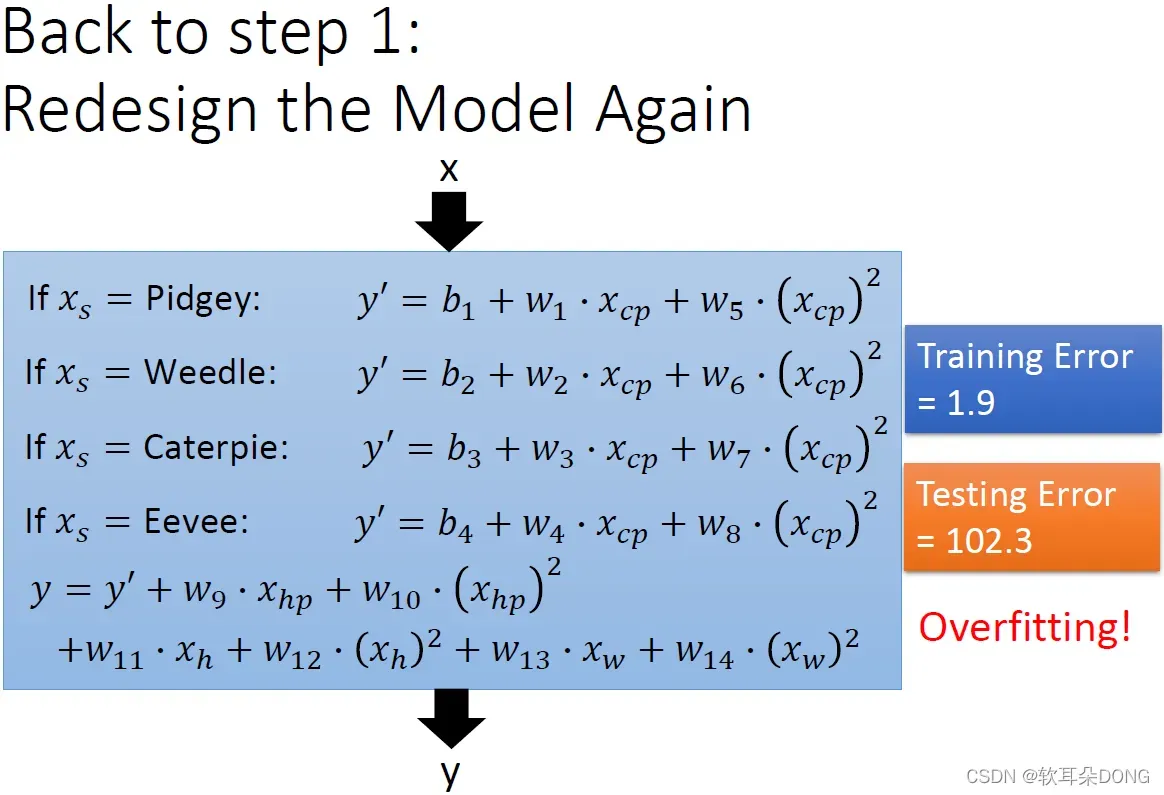
但是我又没有domain knowledge，那怎么办呢？没关系，有一招就是把你所有想到的东西，通通塞进去，我们来弄一个最复杂的function，然后看看会怎样？这个function我写成这样：如果它是波波（Pidgey）的话，它的CP值我们就先计算一个y’，这个y’不是最后这个y，这个y’还要做别的处理才能够变成y。我们就说，如果这个是波波的话，那，我们就是不只要考虑CP值，也要考虑CP值的平方。如果是绿毛虫，用另外一个式子。如果是独角虫，用另外一个式子。如果是伊布，用另外一个式子。

最后我们再把y’做其他的处理，我们把y’，再加上它的生命值（）乘上，再加上生命值的平方（）乘上，再加上高度（）乘上，再加上高度的平方（）乘上，再加上它的weight（）乘上，再加上weight平方（）乘上，这些东西合起来，才是最后output的y：。所以这整个式子里面，其实也没有很多个参数，就是14+4=18，跟你们作业比起来，几百个参数比起来，其实也不是一个太复杂的model。

那我们现在有个这么复杂的function，在training data上我们得到的error，期望应该就是非常的低。我们果然得到一个非常低的error，这个function你可以把它写成线性的式子，就跟刚才一样，这边我就不解释了。那这么一个复杂的function，理论上我们可以得到非常低的training error。training error算出来是1.9，那你可以期待你在testing set上，也算出很低的testing error吗？倒是不见得，这么复杂的model，很有可能会overfitting，你很有可能在testing data上得到很糟的数字。我们今天得到的数值很糟是102.3这样子，结果坏掉了，怎么办呢？如果你是大木博士的话，你就可以删掉一些你觉得没有用的input，然后就得到一个简单的model，避免overfitting的情形。但是我不是大木博士，所以我有用别的方法来处理这个问题。

这招叫做regularization（正则化）。regularization要做的事情是，我们重新定义了step 2的时候，我们对一个function是好还是坏的定义。我们重新redefine我们的loss function，把一些knowledge放进去，让我们可以找到比较好的function。什么意思呢？假设我们的model in general写成这样：，我们原来的loss function，它只考虑了error这件事，原来的loss function只考虑了prediction的结果减掉正确答案的平方，只考虑了prediction的error。

那regularization它就是加上一项额外的term，这一项额外的term是，是一个常数，这个是等一下我们要手调一下看要设多少，那就是把这个model里面所有的都算一下平方以后加起来。那这个合起来（）才是我们的loss function。前面这一项我们刚才解释过，所以我相信你是可以理解的，error越小就代表当然是越好的function。但是，为甚么我们期待一个参数的值越小，参数的值越接近0的function呢？这件事情你就比较难想象，为甚么我们期待一个参数值接近0的function呢？

当我们加上这一项（）的时候，我们就是预期说我们要找到的那个function，它的那个参数越小越好。你知道参数值比较接近0的function它是比较平滑的，所谓的比较平滑的意思是，当今天的输入有变化的时候，output对输入的变化是比较不敏感的。为甚么参数小就可以达到这个效果呢？你可以想想看，假设这个（）是我们的model，现在input有一个变化，比如说：我们对某一个加上，这时候对输出会有什么变化呢？这时候输出的变化就是乘上，你的输入变化，输出就是乘上，你会发现说如果今天你的越小越接近0的话，它的变化就越小。如果越接近0的话，输出对输入就越不sensitive（敏感）。所以今天越接近0，我们的function就是一个越平滑的function。

现在的问题就是，为甚么我们喜欢比较平滑的function？这可以有不同的解释，你可以这样想，如果我们今天有一个比较平滑的function的话，因为平滑的function对输入是比较不敏感的，所以今天如果我们的输入被一些噪声所干扰的话，如果今天噪声干扰的我们的输入，在我们测试的时候，那一个比较平滑的function，它会受到比较少的影响，而给我们一个比较好的结果。

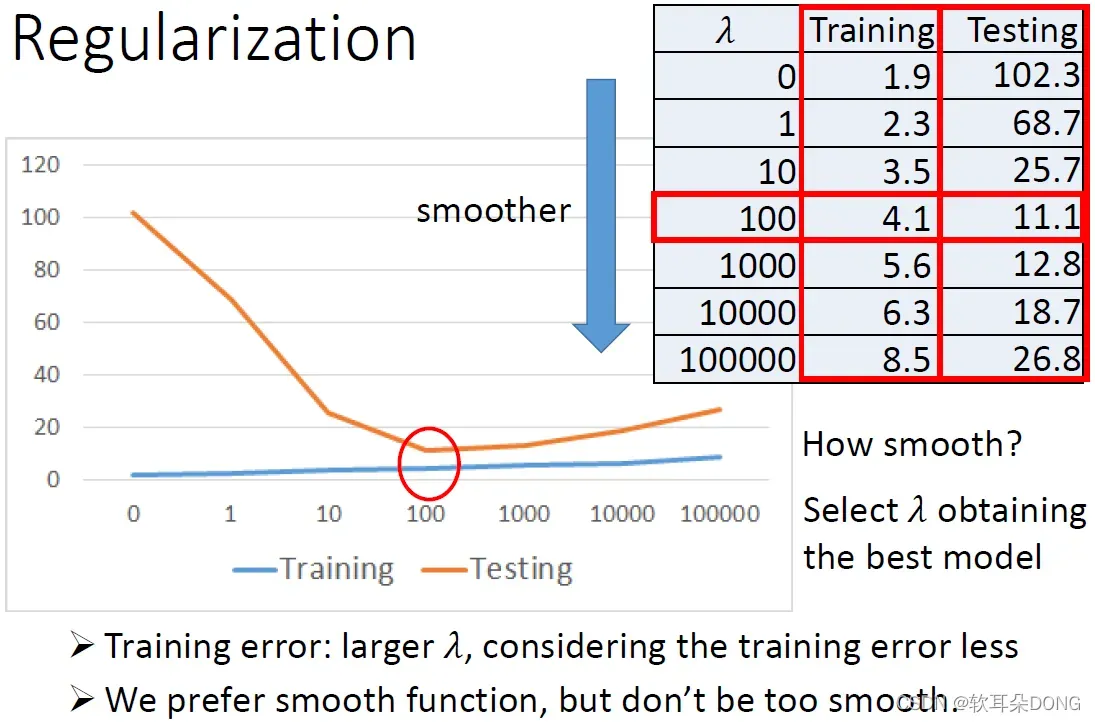
接下来我们就要来看看说，如果我们加入了regularization的项，对我们最终的结果会有甚么样的影响？这个是实验的结果。我们就把λ从0、1、10一直调到100000，我们现在loss有两项，一项是考虑error，一项是考虑多smooth，λ值越大代表考虑smooth的那个regularization那一项它的影响力越大，所以当λ值越大的时候，我们找到的function就越平滑。如果我们看看在training data上的error的话，我们会发现说，如果function越平滑，我们在training data上得到的error其实是越大的。但是这件事情是非常合理的，因为当λ越大的时候，我们就越倾向于考虑w本来的值，我们就倾向考虑w的值而减少考虑我们的error。所以今天如果λ越大的时候，我们考虑error就愈少，所以我们本来在training data上得到的error就越大。但是有趣的是，虽然在training data上得到的error越大，但是在testing data上面得到的error可能是会比较小。比如说我们看这边的例子，原来λ=0，就是没有regularization的时候error是102.3，λ=1就变成68，到λ=10就变成25，到λ=100就变成11.1，但是λ太大的时候，到1000的时候，error又变大变成12.8，一直到26.8。

那这个结果是合理，我们比较喜欢比较平滑的function，比较平滑的function它对noise比较不sensitive，所以当我们增加λ的时候，你的performance是越来越好，但是我们又不喜欢太平滑的function，因为最平滑的function是甚么？最平滑的function就是一条水平线啊，一条水平线是最平滑的function。如果你的function是一条水平线的话，那它啥事都干不成，所以如果今天function太平滑的话，你反而会在testing set上又得到糟糕的结果。所以现在的问题就是，我们希望我们的model多smooth呢？我们希望我们今天找到的function有多平滑呢？这件事情就变成你需要调λ来解决这件事情，你必须要调整λ来决定你的function的平滑程度。比如说你可能调整一下参数以后发现说，今天training都随着λ增加而增加，testing随着λ先减少后增加。在这个地方有一个转折点，是可以让我们的testing error最小，你就选λ=100来得到你的model。

这边还有一个有趣的事实，很多同学其实都知道regularization，你有没有发现，这边（）我没有把b加进去。事实上很多人可能不知道这件事，在做regularization的时候，其实是不需要考虑bias这一项的。首先，如果你自己做实验的话你会发现，不考虑bias，performance会比较好。再来为甚么不考虑bias呢？因为我们今天预期的是，我们要找一个比较平滑的function。你调整bias的这个b的大小，跟一个function的平滑的程度是没有关系的。调整bias值的大小时你只是把function上下移动而已，对function的平滑程度是没有关系的。所以有趣的是，这很多人都不知道，你是不用考虑bias的。总之，搞了半天以后，我最后可以做到，我们的testing error是11.1。

那在我们请助教公告作业之前，我们就说一下今天的conclusion。首先感谢大家来参加我对宝可梦研究的发表会，那我今天得到的结论就是：宝可梦进化后的CP值，跟他进化前的CP值，还有它是哪个物种，是非常有关系的。知道这两件事情几乎可以决定进化后的CP值。但是我认为，可能应该还有其他的factors，我们刚刚看到说我们加上其他甚么高度啊，体重啊，HP以后，是有比较好的，如果我们加入regularization的话。不过我data有点少，所以我没有那么confidence就是了。

然后再来呢就是，我们今天讲了gradient descent的作法，就是告诉大家怎么做，那我们以后会讲它的原理还有技巧。

我们今天讲了overfitting和regularization，介绍一下表象上的现象，未来会讲更多它背后的理论。再来最后我们有一个很重要的问题，首先我觉得我这个结果应该还满正确的，因为你知道网络上有很多的CP的预测器，那些CP的预测器你在输入的时候，你只要输入你的宝可梦的物种和它现在的CP值，它就可以告诉你进化以后的CP值。所以我认为你要预测进化以后的CP值，应该是要知道原来的CP值和它的物种，就可以知道大部分。不过我看那些预测器预测出来的误差，都是给你一个range，它都没有办法给你一个更准确的预测。如果考虑更多的factor更多的input，比如说HP甚么啊，或许可以预测的更准就是了。

但最后的问题就是，我们在testing data上面，在我们testing的10只宝可梦上，我们得到的average error最后是11.1。如果我把它做成一个系统，放到网络上给大家使用的话，你觉得如果我们看过没有看到的data，那我们得到的error会预期高过11.1还是低于11.1，还是理论上期望值应该是一样的。你知道我的training data是里面只有四种，里面都没有甚么乘龙卡比之类的，我们就假设使用者只能够输入那四种，它不会输入乘龙卡比这样。在这个情况下，你觉得如果我们今天把这个系统放到线上，给大家使用的话，我们今天得到的error rate值，会比我今天在testing set上看到的高还是低还是一样？我们之后会解释，我们今天其实用了testing set来选model，就我们今天得到的结果其实是，如果我们真的把系统放在线上的话，预期应该会得到比我们今天看到的11.1还要更高的error rate，这个时候我们需要validation（验证）观念来解决这个问题，这个我们就下一堂课再讲。