【读论文】Learning the Kernel Matrix with Semi-Definite Programming.（2002）
用半定编程学习核矩阵

Gert R. G. Lanckriet，Nello Cristianini，Peter L. Bartlett，Laurent El Ghaoui，Michael I. Jordan

Conference: Machine Learning, Proceedings of the Nineteenth International Conference (ICML 2002), University of New South Wales, Sydney, Australia, July 8-12, 2002

概括

Kernel-based learning algorithms work by embedding the data into a Euclidean space, and then searching for linear relations among the embedded data points. The embedding is performed implicitly, by specifying the inner products between each pair of points in the embedding space.

This information is contained in the so-called kernel matrix, a symmetric and positive semidefifinite matrix that encodes the relative positions of all points. Specifying this matrix amounts to specifying the geometry of the embedding space and inducing a notion of similarity in the input space—classical model selection problems in machine learning.

In this paper we show how the kernel matrix can be learned from data via semidefifinite programming (SDP) techniques. When applied to a kernelmatrix associated with both training and test data this gives a powerful transductive algorithm—using the labeled part of the data one can learn an embedding also for the unlabeled part.

The similarity between test points is inferred from training points and their labels. Importantly, these learning problems are convex, so we obtain a method for learning both the model class and the function without local minima. Furthermore, this approach leads directly to a convex method for learning the 2-norm soft margin parameter in support vector machines, solving an important open problem.

基于内核的学习算法通过将数据嵌入欧几里得空间，然后搜索嵌入数据点之间的线性关系来工作。嵌入是通过指定嵌入空间中每对点之间的内积来隐式执行的。这些信息包含在所谓的核矩阵中，这是一个对称的半正定矩阵，对所有点的相对位置进行编码。指定这个矩阵相当于指定嵌入空间的几何形状，在输入空间中引入相似度的概念。

这些信息包含在所谓的核矩阵中，这是一个对称的半正定矩阵，对所有点的相对位置进行编码。制定这个证明相当于知道了嵌入空间的集合形状，并在入口和出口空间中引入了相似性的概念。机器学习中的经典模型选择问题。

在本文中，外面展示了如何通过半定规划（SDP）技术从数据中学习核矩阵。当应用于与训练和测试数据相关联的核矩阵时，着提供了一种强大的转换算法。使用数据的标记部分，人们也可以为未标记部分学习嵌入。

测试点之间的相似性是从没有训练点及其标签推断出来的。重要的是，这些学习问题是凸的，因此外面获得了一种既可以学习模型类又可以学习没有局部最小值的函数的方法。此外，这种方法直接导致了一种用于学习支持向量机中的2范数软边距参数的凸方法，从而解决了一个重要的开放问题。

关键词

kernel methods, learning kernels, transduction, model selection, support vector machines, convex optimization, semidefifinite programming

核方法、学习核、转导、模型选择、支持向量机、凸优化、半定规划

综上所述

In this paper we have presented a new method for learning a kernel matrix from data. Our approach makes use of semidefifinite programming (SDP) ideas. It is motivated by the fact that every symmetric, positive semidefifinite matrix can be viewed as a kernel matrix (corresponding to a certain embedding of a fifinite set of data), and the fact that SDP deals with the optimization of convex cost functions over the convex cone of positive semidefifinite matrices (or convex subsets of this cone). Thus convex optimization and machine learning concerns merge to provide a powerful methodology for learning the kernel matrix with SDP.

We have focused on the transductive setting, where the labeled data are used to learn an
embedding, which is then applied to the unlabeled part of the data. Based on a new generalization
bound for transduction, we have shown how to impose convex constraints that effffectively control
the capacity of the search space of possible kernels and yield an effiffifficient learning procedure that can be implemented by SDP.

Furthermore, this approach leads to a convex method to learn the 2-norm soft margin parameter in support vector machines, solving an important open problem.

Promising empirical results are reported on standard benchmark datasets; these results show that
the new approach provides a principled way to combine multiple kernels to yield a classififier that is comparable with the best inpidual classififier, and can perform better than any inpidual kernel.

Performance is also comparable with a classififier in which the kernel hyperparameter is tuned with cross-validation; our approach achieves the effffect of this tuning without cross-validation.

We have also shown how optimizing a linear combination of kernel matrices provides a novel method for fusing heterogeneous data sources. In this case, the empirical results show a signifificant improvement of the classifification performance for the optimal combination of kernels when compared to inpidual kernels.

There are several challenges that need to be met in future research on SDP-based learning algo rithms. First, it is clearly of interest to explore other convex quality measures for a kernel matrix, which may be appropriate for other learning algorithms. For example, in the setting of Gaussian processes, the relative entropy between the zero-mean Gaussian process prior P with covariance kernel K and the corresponding Gaussian process approximation Q to the true intractable posterior process depends on K as

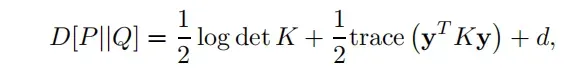
where the constant d is independent of K。One can verify that D[P||Q] is convex with respect to R = K−1 (see, e.g., Vandenberghe et al., 1998)。Minimizing this measure with respect to R, and thus K, is motivated from PAC-Bayesian generalization error bounds for Gaussian processes (see, e.g., Seeger, 2002) and can be achieved by solving a so-called maximum-determinant problem (Vandenberghe et al., 1998)—an even more general framework that contains semidefifinite programming as a special case.

Second, the investigation of other parameterizations of the kernel matrix is an important topic for further study. While the linear combination of kernels that we have studied here is likely to be useful in many practical problems—capturing a notion of combining Gram matrix “experts”—it is also worth considering other parameterizations as well.

Any such parameterizations have to respect the constraint that the quality measure for the kernel matrix is convex with respect to the parameters of the proposed parameterization. One class of examples arises via the positive defifinite matrix completion problem (Vandenberghe et al., 1998). Here we are given a symmetric kernel matrix K that has some entries which are fifixed.

The remaining entries—the parameters in this case—are to be chosen such that the resulting matrix is positive defifinite, while simultaneously a certain cost function is optimized, e.g., trace(SK) + log det K−1, where S is a given matrix。This specifific case reduces to solving a maximum-determinant problem which is convex in the unknown entries of K, the parameters of the proposed parameterization.

A third important area for future research consists in fifinding faster implementations of semidef inite programming. As in the case of quadratic programming (Platt, 1999), it seems likely that special purpose methods can be developed to exploit the exchangeable nature of the learning problem in classifification and result in more effiffifficient algorithms.

Finally, by providing a general approach for combining heterogeneous data sources in the setting of kernel-based statistical learning algorithms, this line of research suggests an important role for kernel matrices as general building blocks of statistical models.

Much as in the case of fifinite dimensional suffiffifficient statistics, kernel matrices generally involve a signifificant reduction of the data and represent the only aspects of the data that are used by subsequent algorithms.

Moreover,given the panoply of methods that are available to accommodate not only the vectorial and matrix data that are familiar in classical statistical analysis, but also more exotic data types such as strings, trees and graphs, kernel matrices have an appealing universality.

It is natural to envision libraries of kernel matrices in fifields such as bioinformatics, computational vision, and information retrieval, in which multiple data sources abound. Such libraries would summarize the statistically-relevant features of primary data, and encapsulate domain specifific knowledge. Tools such as the semidefifinite programming methods that we have presented here can be used to bring these multiple data sources together in novel ways to make predictions and decisions.

在本文中，我们提出了一种从数据中学习核矩阵的新方法。我们的方法利用了半定规划 (SDP) 思想。它的动机是每个对称的半正定矩阵都可以被视为一个核矩阵（对应于有限数据集的某种嵌入），以及 SDP 处理凸成本函数在凸正半定矩阵的锥体（或该锥体的凸子集）。因此，凸优化和机器学习关注点合并，为使用 SDP 学习内核矩阵提供了强大的方法。

我们专注于转导设置，其中标记数据用于学习嵌入，然后将其应用于数据的未标记部分。基于一个新的转导泛化界，我们展示了如何施加凸约束，有效控制可能内核的搜索空间的容量，并产生一个可以由 SDP 实现的有效学习过程。

此外，这种方法导致了一种凸方法来学习支持向量机中的 2 范数软边距参数，从而解决了一个重要的开放问题。

在标准基准数据集上报告了有希望的经验结果；这些结果表明，新方法提供了一种原则性的方法，可以将多个内核组合起来，以产生与最好的单个分类器相媲美的分类器，并且优于任何单个内核的性能更好。

性能也可与使用交叉验证来调整内核超参数的分类器相媲美；我们的方法在没有交叉验证的情况下实现了这种调整的效果。

我们还展示了优化内核矩阵的线性组合如何提供一种融合异构数据源的新方法。在这种情况下，经验结果表明，与单个核相比，核的最佳组合的分类性能显着提高。

在基于 SDP 的学习算法的未来研究中需要解决几个挑战。首先，探索核矩阵的其他凸质量度量显然是有意义的，这可能适用于其他学习算法。例如，在高斯的设置中过程中，具有协方差核 K 的零均值高斯过程先验 P 和对应的高斯过程近似 Q 对真正的棘手后验过程的相对熵取决于 K 为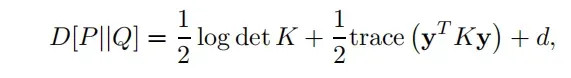

其中常数 d 与 K 无关。可以验证 D[P||Q] 相对于 R = K‑1是凸的（例如，参见 Vandenberghe 等人，1998 年）。最小化这个关于 R 的度量，因此 K 是由高斯过程的 PAC‑贝叶斯泛化误差界限激发的（参见，例如，Seeger，2002），并且可以通过解决所谓的最大行列式问题来实现（Van denberghe et al., 1998)。一个更通用的框架，其中包含作为特例的半定规划。

其次，核矩阵的其他参数化的研究是进一步研究的重要课题。虽然我们在这里研究的内核的线性组合可能在许多实际问题中很有用。捕获组合 Gram 矩阵“专家”的概念。 但也值得考虑其他参数化。

任何这样的参数化都必须尊重核矩阵的质量度量相对于所提出的参数化的参数是凸的这一约束。一类例子是通过正定矩阵完成问题（Vandenberghe et al., 1998）产生的。在这里，我们给出了一个对称核矩阵 K，它有一些固定的条目。

剩下的条目在这种情况下是参数将被选择为使得结果矩阵是正宗的，同时优化某个成本函数，例如，trace(SK) + log det K‑1 ，其中 S 是给定的矩阵.这种特殊情况简化为解决最大行列式问题，该问题在 K 的未知条目中是凸的，K 是建议参数化的参数。

未来研究的第三个重要领域是寻找更快的半定义编程实现。与二次规划 (Platt, 1999) 的情况一样，似乎可以开发特殊用途的方法来利用分类中学习问题的可交换性并产生更有效的算法。

最后，通过提供一种在基于核的统计学习算法设置中组合异构数据源的通用方法，该研究方向证明了核矩阵作为统计模型的通用构建块的重要作用。

与有限维度中足够统计的情况一样，核矩阵通常会显着减少数据，并代表后续算法使用的数据的唯一方面。

此外，核矩阵具有吸引人的通用性，考虑到各种方法不仅可以容纳来自经典统计分析的熟悉的向量和矩阵数据，还可以容纳更奇特的数据类型，例如字符串、树和图。

在生物信息学、计算视觉和信息检索等多个数据源比比皆是的领域中，自然地设想了内核矩阵库。这样的库将总结原始数据的统计相关特征并封装特定领域的知识。我们在这里介绍的半定编程方法等工具可用于以新颖的方式组合这些多个数据源，以进行预测和决策。

[1] Lanckriet G R G , Cristianini N , Bartlett P L , et al. Learning the Kernel Matrix with Semi-Definite Programming[C]// Machine Learning, Proceedings of the Nineteenth International Conference (ICML 2002), University of New South Wales, Sydney, Australia, July 8-12, 2002. 2002.