1. AI技术聚合首页
  2. 技术文章

机器学习——猫狗识别（入门案例）

心中带点小风骚 • • 技术文章 • 阅读 330

案例研究：下载猫和狗的图片并对其进行分类。对数据、训练集和测试集进行分类。
训练集和测试集都按约定命名，猫记为1，狗记为0。
处理流程：数据处理，把数据处理为64X64大小的格式，参数初始化分被初试化 各层权重 W 和 偏置 b，（一般情况下W进行随机赋值，b赋值为1），前向传播，确定激活函数（浅层选择tanh函数，深层选择ReLu），交叉熵损失，反向传播（梯度下降），更新参数，构建神经网络，训练进行测试，进行优化（后面还会更新的）。
包装参考：

import os
from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
import skimage.io as io

数据处理：

机器学习——猫狗识别（入门案例）

def clean(path, save_path, w=64,h=64):
    """

    :param path: 读取图片的路径
    :param save_path: 存放图片的路径
    :param w: 图片宽度
    :param h: 图片高度
    :return:
    """

    if not os.path.exists(save_path):
        os.mkdir(save_path)
    file_names = os.listdir(path) # 获取路径下所有文件的名字

    for file_name in file_names:
        bl_dir = os.path.isdir(path + "/" + file_name)
        if bl_dir:
            lower_directory = path + "/" + str(file_name)
            save_ds = save_path + "/" + str(file_name)
            if not os.path.exists(save_ds):
                os.mkdir(save_ds)
            lower_directory_names = os.listdir(lower_directory)
        else:
            lower_directory = path
            lower_directory_names = file_names

        for lower_directory_name in lower_directory_names:

            # # print(save_name)
            bl_save_dir = os.path.isdir(lower_directory + "/" + lower_directory_name)
            photo_path = lower_directory + "/" + lower_directory_name
            save_name = lower_directory + "/" + lower_directory_name

            try:
                pic = Image.open(photo_path)
                pic = pic.resize((w, h))

                pic.save(save_name)

                print("成功")
            except:
                print("fail")

参数初始化

def initialize_parameters(layer_dims):
    """
	W权重进行随机，b初始化为1
    :param layer_dims: 网络层神经元个数
    :return: 储存参数的字典
    """
    np.random.seed(5)

    parameters = {}

    L = len(layer_dims)

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.1
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))

    return parameters

前向传播

def relu(Z):
    """
	深度网络选择Relu
    :param Z: 激活函数输入 神经元线性输出
    :return: A 激活函数输出，神经元非线性输出
    """
    A = np.maximum(0, Z)

    return A


def sidmoid(Z):

    """
	浅层网络 sidmoid
    :param Z: 激活函数输入 神经元线性输出
    :return: A 激活函数输出，神经元非线性输出
    """
    A = 1 / (1 + np.exp(-Z))

    return A
# 前向传播
def single_layer_forward(A_prev, W, b, activation):
    """

    :param A_prev: 该网络的输入，上层网络的输出
    :param W: 该层网络的权重
    :param b: 该层网络的偏置参数
    :param activation: 激活函数
    :return: A 该网络的输出层
           cache: 储存所有的中间变量 A_prev W b Z
    """

    Z = np.dot(W, A_prev) + b
    if activation == "sigmoid":
        A = sidmoid(Z)
    elif activation == "relu":
        A = relu(Z)
    cache = (A_prev, W, b, Z)

    return A , cache
    def forward_propagation(X, parameters):
    """

    :param X: 神经网络的输入
    :param parameters:  该层网络的权重数据
    :return:  A 该层网络的输出  cache 储存该层网络所有的中间变量
    """

    caches = []
    A = X
    L = len(parameters)   # 因为有wb两个，所以需要除以2
    L = int(L/2)
    for l in range(1, L):
        A_prev = A
        A, cache = single_layer_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], "relu")

        caches.append(cache)

    Al, cache = single_layer_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], "sigmoid")
    caches.append(cache)

    return Al, caches

交叉熵损失

def compute_cost(AL, Y):
    """

    :param AL:神经网络输出层输出
    :param Y: 神经网络真是标签
    :return: 交叉熵损失
    """
    m = AL.shape[1]
    cross_entropy = -(Y * np.log(AL) + (1 - Y) * np.log(1 - AL))
    cost = 1.0 / m * np.sum(cross_entropy)

    return cost

反向传播

def relu_backward(dA, Z):
    """

    :param dA: A 的梯度
    :param z: 神经网络的输出
    :return: dZ Z的梯度
    """

    dZ = np.array(dA, copy=True)
    dZ[Z <= 0] = 0

    return dZ

def sigmoid_backward(dA, Z):
    """

    :param dA:A 的梯度
    :param Z: 神经网络的输出
    :return: dZ Z的梯度
    """
    s = 1/ (1 + np.exp(-Z))
    dZ = dA * s * (1-s)
    return dZ

def single_layer_backward(dA, cache, activation):
    """
    :param dA:A 的梯度
    :param cache: 储存所有中间变量 A_prev W b Z
    :param activation: 选择的激活函数
    :return: dA_prev 上一层A_prev 的梯度 dW 参数W的梯度 db 参数b梯度
    """
    A_prev, W, b, Z = cache
    if activation == "relu":
        dZ = relu_backward(dA, Z)
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, Z)

    m = dA.shape[1]
    dW  = 1/m*np.dot(dZ, A_prev.T)
    db = 1 / m * np.sum(dZ, axis=1, keepdims=True)
    dA_prev = np.dot(W.T, dZ)
    return dA_prev, dW, db

def backward_propagarion(AL, Y, caches):
    """

    :param AL: 神经网络输出的层数
    :param cache:  储存所有中间变量 A_prev W b Z
    :param Y：真实标签
    :return: grads 所有参数梯度
    """
    gards = {}
    L = len(caches)
    m = AL.shape[1]

    dAL = -(np.pide(Y, AL) - np.pide(1 - Y , 1 - AL))
    current_cache = caches[L-1]
    gards["dA" + str(L-1)],gards["dW" + str(L-1)], gards["db" + str(L-1)] = single_layer_backward(dAL, current_cache, activation="sigmoid")

    for l in reversed(range(L-1)):
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = single_layer_backward(gards["dA" + str(l + 1)], current_cache, activation="relu")
        gards["dA" + str(l)] = dA_prev_temp
        gards["dW" + str(l)] = dW_temp
        gards["db" + str(l)] = db_temp

    return gards

更新参数


def update_parameters(parameters, grads, learning=0.1):
    """

    :param parameters: 网络参数
    :param grads: 神经网络参数梯度
    :param learning: 学习速率
    :return: 网络参数
    """

    L = len(parameters)
    L = int(L/2)
    for l in range(L):
        parameters["W" +str(l+1)] -= learning * grads["dW" + str(l)]
        parameters["b" +str(l+1)] -= learning * grads["db" + str(l)]

    return parameters

建立模型

def nn_model(X, Y, layers_dims, num_iterations=300, learning_rate=0.01,):
    """

    :param X:神经网络输入
    :param Y: 样本标签
    :param layers_dims:神经网络各层神经元个数，包括输入层和输出层
    :param learning_rate: 学习速率
    :param num_iterations: 学习率
    :return:  训练完成后的网络模型
    """

    np.random.seed(1)
    costs = []

    parameters = initialize_parameters(layers_dims)

    for i in range(num_iterations):
        AL, caches = forward_propagation(X, parameters)
        cost = compute_cost(AL, Y)
        grads = backward_propagarion(AL, Y, caches)

        parameters = update_parameters(parameters, grads, learning_rate)

        if (i+1) % 100 == 0:
            print("Cost after iteration %i : %f" % (i+1, cost))
            costs.append(cost)

    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('loop humber')
    plt.title("learning" + str(learning_rate))
    plt.show()
    plt.close()

    return parameters

作出预测

def predit(X, parameter):
    """

    :param X:神经网络输入
    :param parameter: 训练完成后的网络参数
    :return: 预测样本标签
    """

    AL, caches = forward_propagation(X, parameter)
    Y_pred = np.zeros((1, X.shape[1]))
    Y_pred[AL > 0.5] = 1

    return Y_pred

if __name__ == "__main__":
    layers_dims = [64*64*3, 200, 100, 10, 1]
    X_train, Y_train, X_test, Y_test = normalization()
    parameters = nn_model(X_train, Y_train, layers_dims, num_iterations=2000, learning_rate=0.01)
    # print(parameters)


    Y_test_pred = predit(X_test, parameters)
    print(Y_test_pred)
    print("*" * 50)
    print(Y_test)
    acc_test = np.mean(Y_test_pred == Y_test)
    print("测试数据的精确度为：%f " % (acc_test))

运行结果：网络结构（输入层 隐藏层（1） 输出层）迭代1000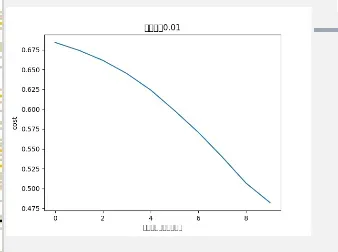
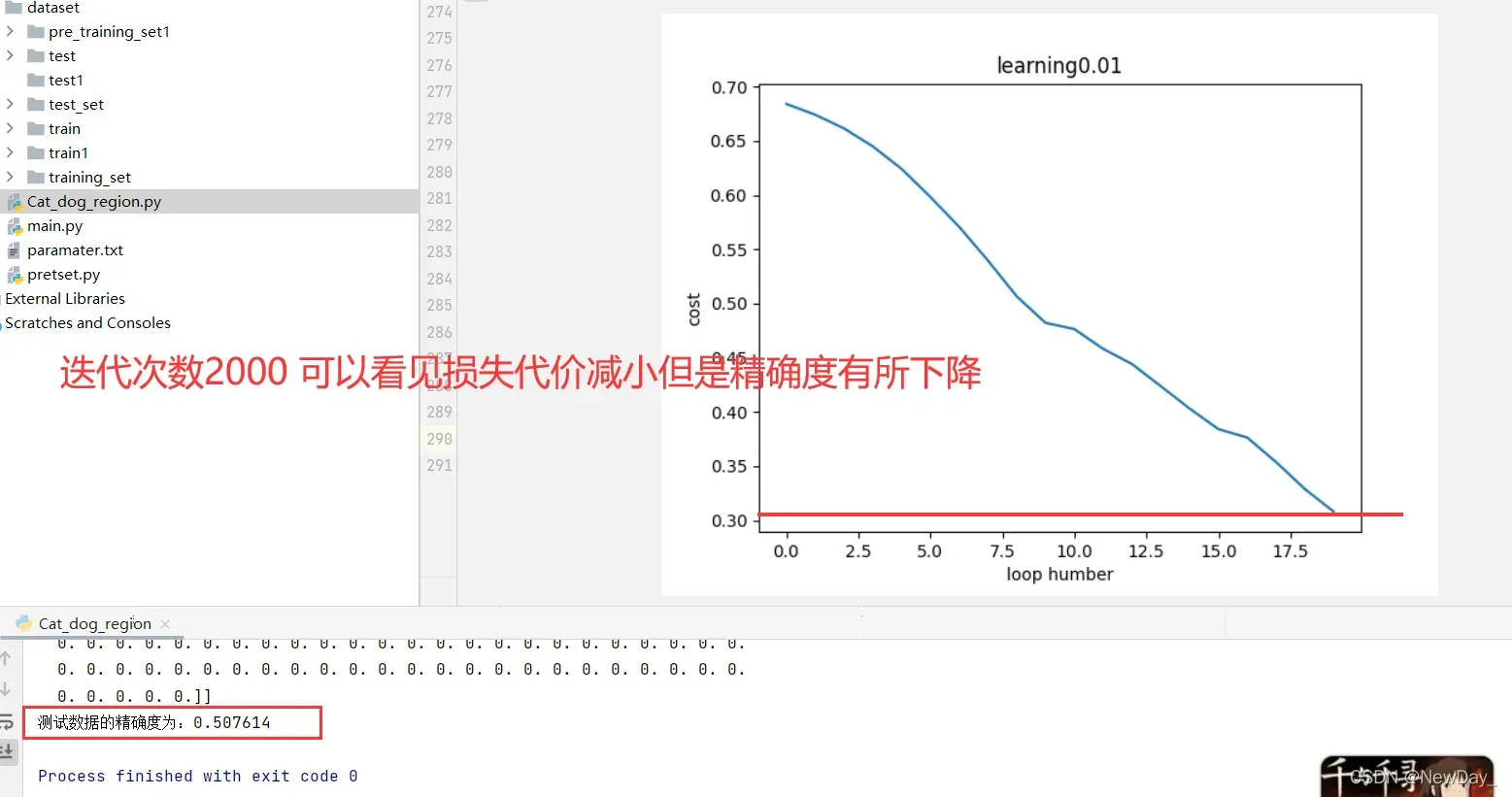
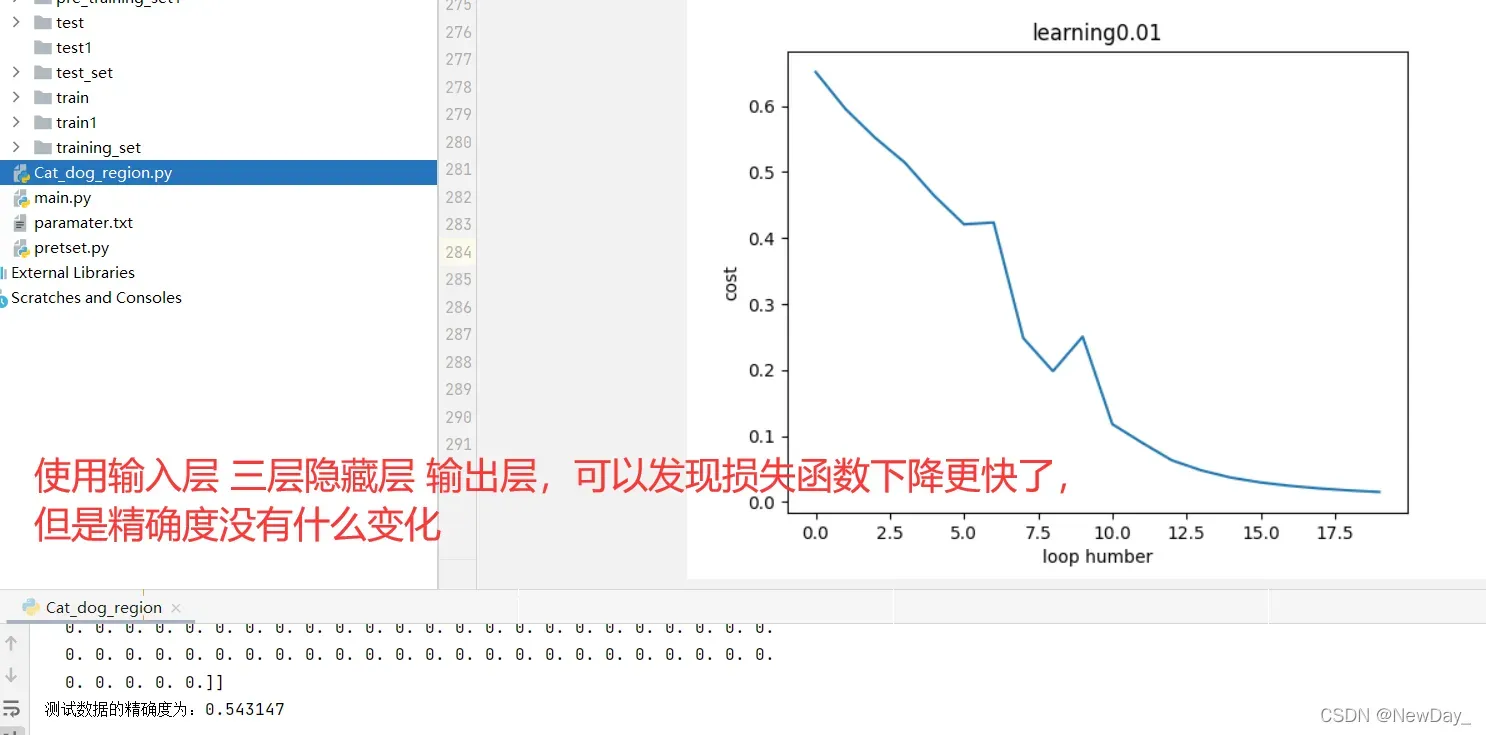
机器学习——猫狗识别（入门案例）

机器学习——猫狗识别（入门案例）
机器学习——猫狗识别（入门案例）
机器学习——猫狗识别（入门案例）
参考书目：深度学习入门（基于pytorch和TensorFlow的理论与实现）

文章出处登录后可见！

已经登录？立即刷新

共计人评分，平均分

到目前为止还没有投票！成为第一位评论此文章。

赞 (0)
心中带点小风骚的头像心中带点小风骚普通用户
0
上一篇 2022年3月16日
下一篇 2022年3月17日

相关推荐