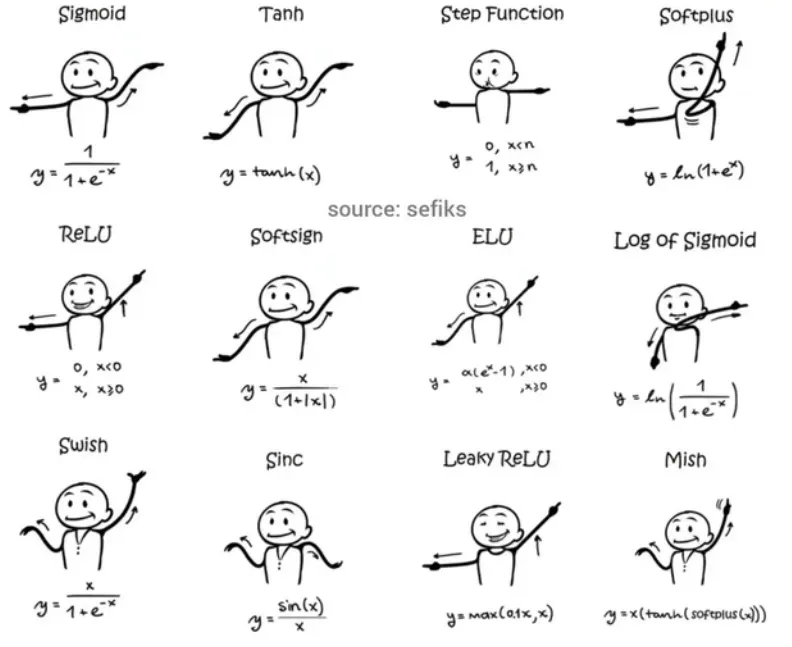
基本概念

单层求导

f为激活函数
激活函数与Pytorch

作用

激活函数对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用，它们将非线性特性引入到我们的网络中。

如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机（Perceptron）。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。

如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

Me：增加非线性运算，增强拟合能力

梯度饱和

梯度饱和常常是和激活函数相关的，比如sigmod和tanh就属于典型容易进入梯度饱和区的函数，即自变量进入某个区间后，梯度变化会非常小，表现在图上就是函数曲线进入某些区域后，越来越趋近一条直线，梯度变化很小，梯度饱和会导致训练过程中梯度变化缓慢，从而造成模型训练缓慢。

以0为中心

因为输出不以0为中心的激活函数，比如sigmoid函数，其输出都为正，意味着在梯度下降时对某权重1到权重n的导数要么全为正，要么全为负。这会导致梯度下降呈z字型，增加了迭代次数，降低了收敛速度

Sigmoid

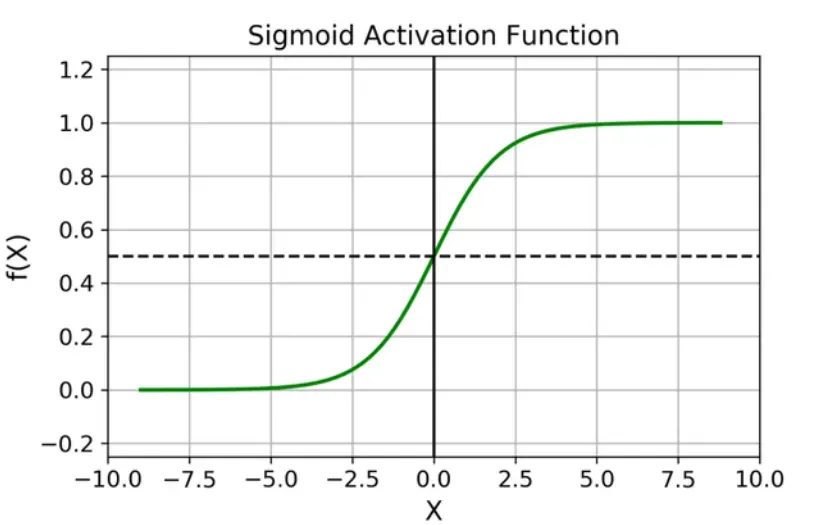
缺点：
容易梯度饱和后梯度消失；
函数输出不是以 0 为中心的，这会降低权重更新的效率；
Sigmoid 函数执行指数运算，计算机运行得较慢。

Tanh/双曲正切

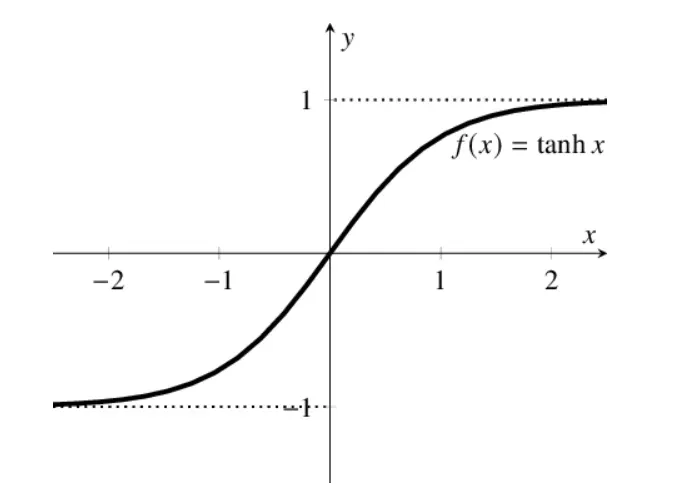
在一般的二元分类问题中，tanh 函数用于隐藏层，而 sigmoid 函数用于输出层，但这并不是固定的，需要根据特定问题进行调整。

ReLU/整流线性单元

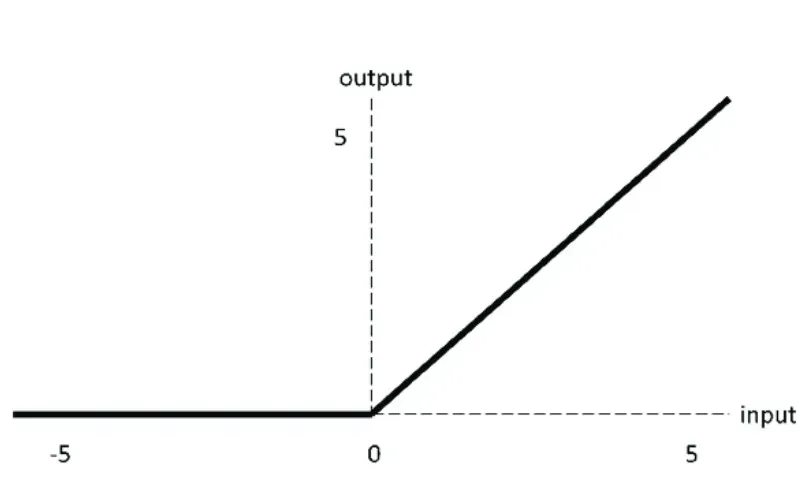
缺点：
Dead ReLU 问题。当输入为负时，ReLU 完全失效，在正向传播过程中，这不是问题。有些区域很敏感，有些则不敏感。但是在反向传播过程中，如果输入负数，则梯度将完全为零，sigmoid 函数和 tanh 函数也具有相同的问题；
ReLU 函数不是以 0 为中心的函数。

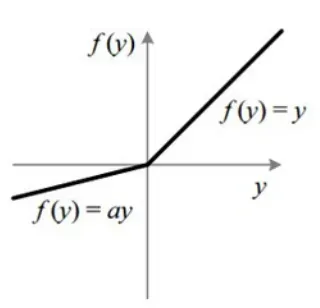
Leaky ReLU/LReLU/渗透整流线性单元

ELU

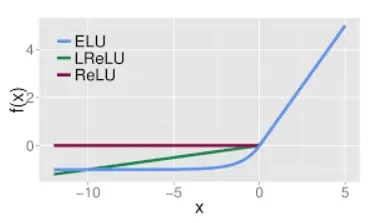
与 Leaky ReLU 类似，尽管理论上比 ReLU 要好，但目前在实践中没有充分的证据表明 ELU 总是比 ReLU 好。

Parametric ReLU/PReLU/参数化整流线性单元

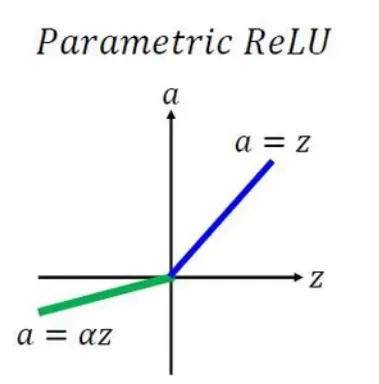
优点：
在负值域，PReLU 的斜率较小，这也可以避免 Dead ReLU 问题。
与 ELU 相比，PReLU 在负值域是线性运算。尽管斜率很小，但不会趋于 0。

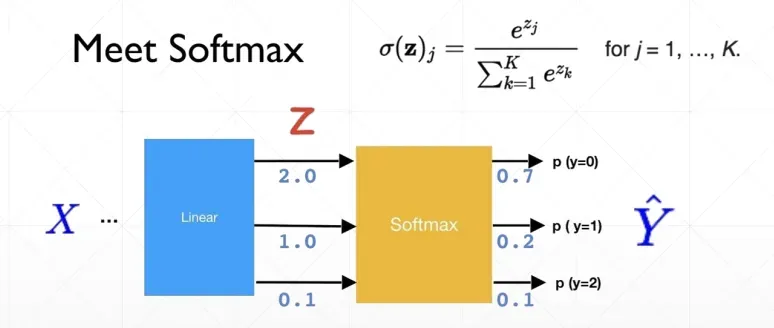
Softmax

大的相对更大，小的相对更小，但不改变相对的大小关系，一般对分类任务的输出进行处理

缺点：
在零点不可微；
负输入的梯度为零，这意味着对于该区域的激活，权重不会在反向传播期间更新，因此会产生永不激活的死亡神经元。

Swish

激活函数与Pytorch
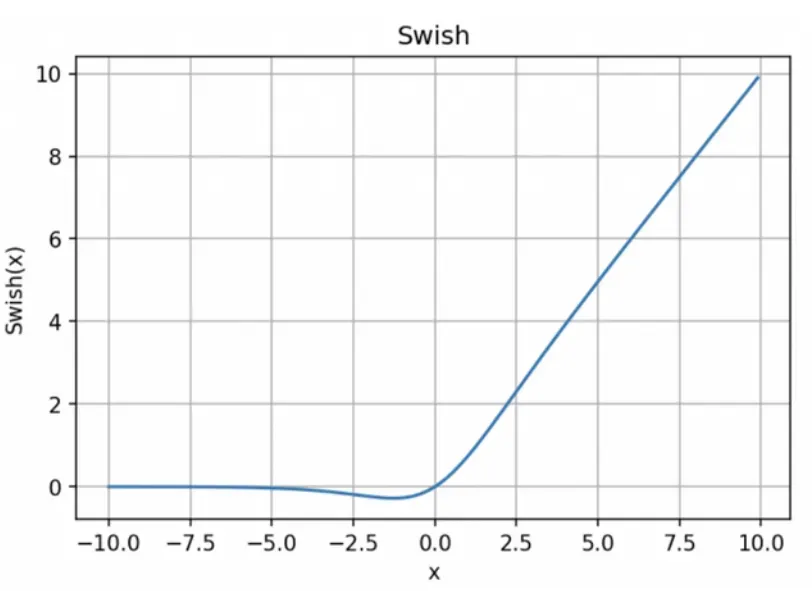
优点：
「无界性」有助于防止慢速训练期间，梯度逐渐接近 0 并导致饱和；（同时，有界性也是有优势的，因为有界激活函数可以具有很强的正则化，并且较大的负输入问题也能解决）；
导数恒 > 0；平滑度在优化和泛化中起了重要作用。

Maxout

https://www.bilibili.com/video/BV1bD4y1d7Zz?spm_id_from=333.337.search-card.all.click

maxout单元进一步扩展了整流线性（ReLU）单元。maxout单元将z划分为每组具有k个值的组，而不是使用作用于每个元素的函数g (z)。每个maxout单元则输出每组中的最大元素。
激活函数与Pytorch
i是组号索引，j是组内号索引。

例如，我们要得到一个3输入2输出的结构：

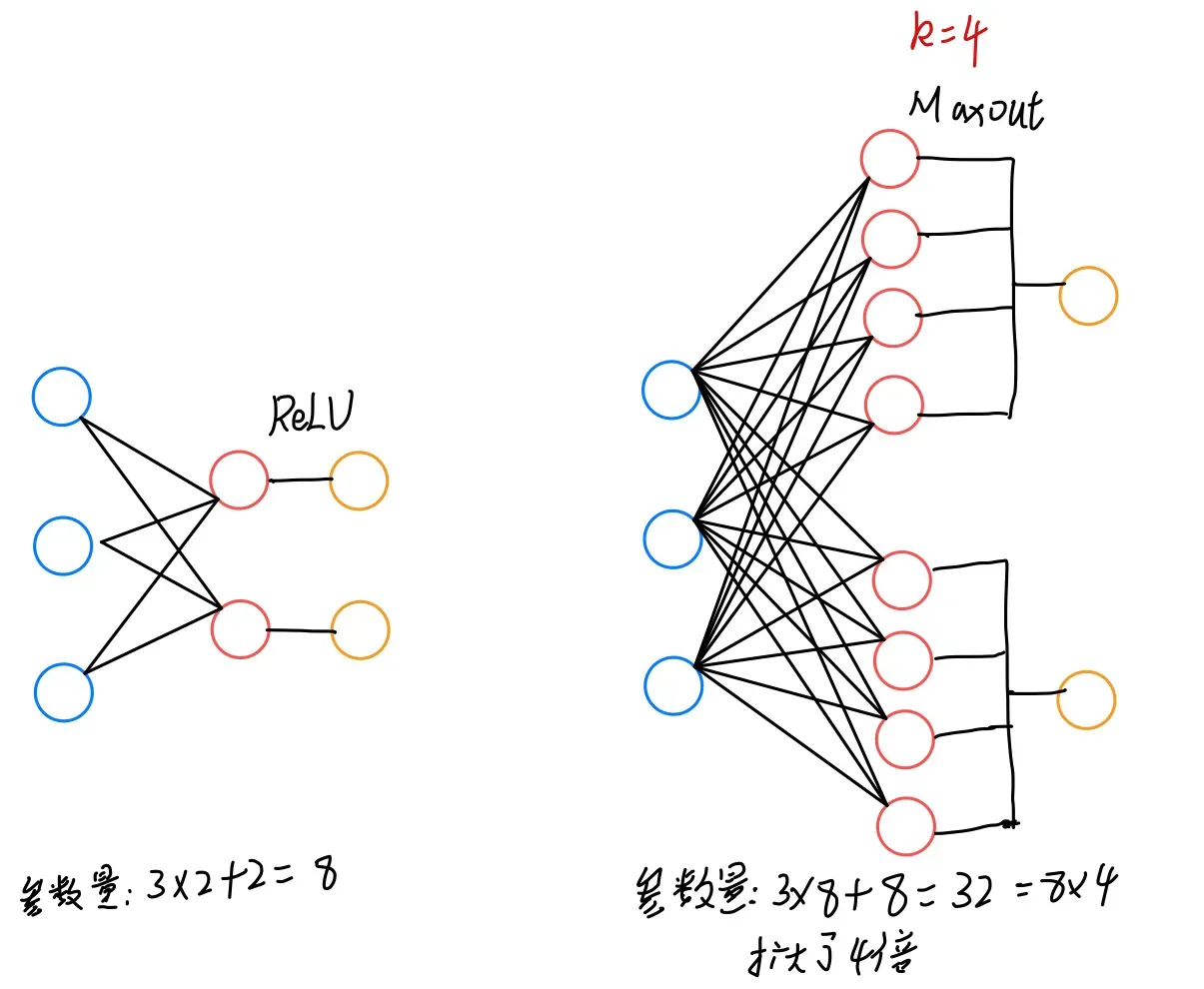
maxout单元可以学习具有多达k段的分段线性的凸函数。maxout单元因此可以视为学习激活函数本身，而不仅仅是单元之间的关系。使用足够大的k，maxout单元可以以任意的精确度来近似任何凸函数。

特别地，具有两块的maxout层可以学习实现和传统层相同的输入x的函数，这些传统层可以使用整流线性激活函数、绝对值整流、渗漏整流线性单元或参数化整流线性单元，或者可以学习实现与这些都不同的函数。Me：ReLU，绝对值整流，LReLU，PReLU是2分段函数，所有k=2就可以拟合到

maxout层的参数化当然也将与这些层不同，所以即使是maxout学习去实现和其他种类的层相同的x的函数这种情况下，学习的机理也是不一样的。

代码

import torch
from torch import nn
from torch.nn import functional as F

inputs = torch.randn(2, 4)

print(F.sigmoid(inputs))

print(F.tanh(inputs))

print(F.relu(inputs))

print(F.leaky_relu(inputs, negative_slope=0.01))

print(F.elu(inputs, alpha=1.0))

# num_parameters 可学习的参数a的个数，只有两个合法的取值：1（默认）2 the number of channels
m = nn.PReLU(num_parameters=1)
print(m(inputs))

print(F.softmax(inputs, dim=1))

# swish
print(inputs * F.sigmoid(inputs))
a=1.0))

# num_parameters 可学习的参数a的个数，只有两个合法的取值：1（默认）2 the number of channels
m = nn.PReLU(num_parameters=1)
print(m(inputs))

print(F.softmax(inputs, dim=1))

# swish
print(inputs * F.sigmoid(inputs))

文章出处登录后可见！

已经登录？立即刷新

激活函数与Pytorch