本文提出直接学习一种插值方法，该方法由多尺度DNN建模，用于从极坐标系中的可用系数预测笛卡尔坐标系中的二维傅里叶系数。实验表明，与现有的基于DNN的解相比，所提出的基于DNN的傅立叶插值方法不仅具有最先进的性能，而且计算效率更高。
拟议方法中不涉及投影或反投影。在性能评估方面，将所提出的方法与FBP、TV方法以及两种深层CT重建方法：LEARN方法和LEARN-PD方法进行了比较。实验表明，该方法的性能明显优于这些方法，同时需要更少的训练时间。
二维离散傅立叶域中的插值问题，即从极坐标上的可用测量值估计笛卡尔坐标上的所有二维傅立叶系数，确实是一个具有挑战性的问题。它不能简单地用经典的数值插值格式来解决，例如线性插值。主要原因是图像的二维傅立叶系数高度不规则，这与经典插值方法所作的局部平滑假设相矛盾（本文探讨的主要问题）。因此，直接调用经典插值方案将导致非常错误的结果，并产生明显的伪影。在稀疏视图CT的情况下，可用测量沿有限的角度稀疏，结果可能更糟。Zhang和Froment提出了用图像的全变差（TV,2005）正则化来解决这种插值问题。虽然CT重建中引入的许多其他正则化技术（引文13、15、16、19、9、11、6，应该是只基于迭代获得正则项的方法），也可用于在离散傅立叶域中正则化插值，但这些正则化策略基于一些预定义的图像先验，这在实践中并不总是成立的（正则项的典型缺陷）。近年来，基于DNN的深度学习已成为CT图像重建的有力工具。通过处理通过某种方法重建的图像中的伪影，早期的工作使用DNN作为强大的去噪器来去除结果中的伪影（引文8 12 18 20均是基于DL的图像后处理方法）。最近，基于DNN的先验优化展开成为一种更优选的方法；（引文1、3、10、17、7、4、5主要使用‘DL+迭代’对正则项进行学习)这些方法采用迭代正则化方法，用参数可学习的DNN代替正则化相关模块。注意，在每次迭代中，这些方法需要执行投影和反投影操作，即Radon变换（1）和it伴随算子。由于这些操作的计算代价很高，在网络中包含多个这样的操作不仅使计算非常耗时，而且还增加了网络训练的复杂性（通过‘DL+迭代’学习正则对高噪作拉动的方法的典型缺陷）。
本文方法思想：
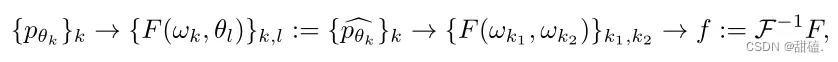
θ表示扫描范围[0，]，
表示在
位置上的投影数据。
上述过程中的关键步骤是以稀疏视图下的估计一个完备的
(图注：①表示扫描角为
、
个采样点下的正弦图，即稀疏视角CT的正弦图；
② 表示对①作一维傅里叶变换后的结果；
③ 表示对图像(但图中看起来是将②极坐标化的样子)作二维傅里叶变换；
④ 表示对③进行插值后的结果；(此处插值方法还未完全确定)
⑤ 表示重建结果。)
本文方法内容：
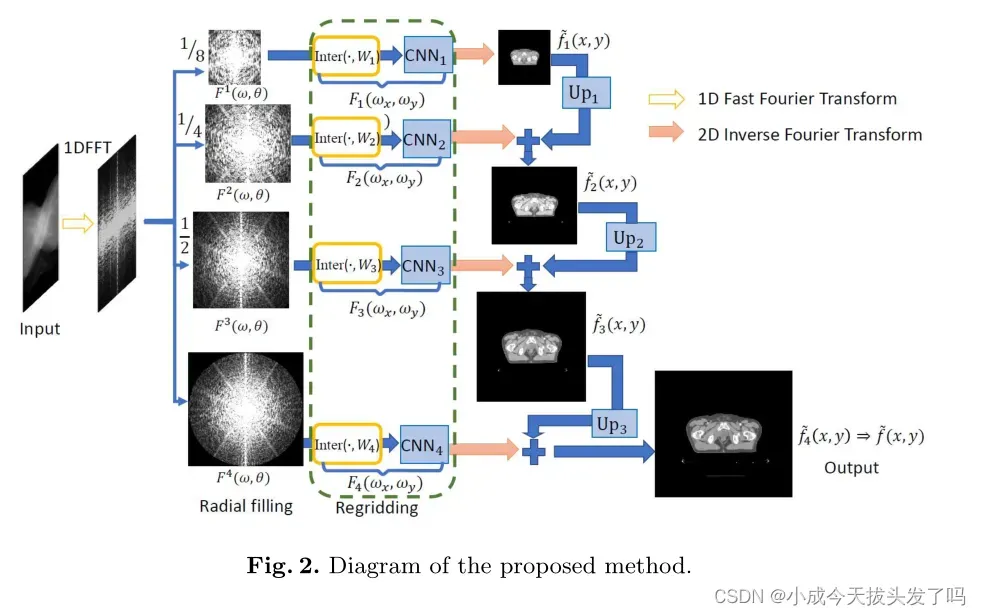
本文提出了一种可学习的离散傅立叶域网格重置方法，该方法排除了网络中的前向/后向投影。其基本思想是使用具有自适应权重的邻域加权和来插值缺失的傅立叶系数。具体而言，对于笛卡尔网格上的频率，缺失系数是通过其K个最近邻居的加权平均值
在极坐标网格上预测的：
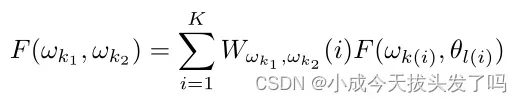
其中是可学习的权重，可适应不同的频率。这种插值方案以多尺度方式实现。对于极坐标中密集邻接的低频段，取一个较小的K使得少部分邻接被用于插值。对于极坐标中稀疏邻接的高频段，取一个较大的K使得更多邻接用于插值。(原文描述：For low frequencies with dense neighbors in polar coordinates, few neighbors are used for interpolation with smaller K. For high frequencies with sparse neighbors in polar coordinates, more neighbors are used for interpolation with larger K.)
插值完成后，在笛卡尔网格上对所有傅立叶系数进行初始估计。然后，引入可学习的CNN来修正插值过程中可能出现的预测误差。由于从低频到高频的过程预测精度下降，我们提出了一种基于多尺度CNN的校正方案。简单地说，我们在极坐标网格上构造了S组傅里叶系数，其范围从低频增加到高频，表示为。然后，在离散傅立叶域内进行插值和基于CNN的校正后，图像可以通过离散傅里叶逆变换在不同分辨率上被重建。并非是直接在分辨率为s的步骤中使用预测结果来估计图像f，而是在上采样之后通过将当前的估计结果与分辨率为s-1的结果进行融合。(翻译水平有限，此处应该有问题)。总之，对于每个分辨率s，图像f的结果预测（由
表示）可以表示为：
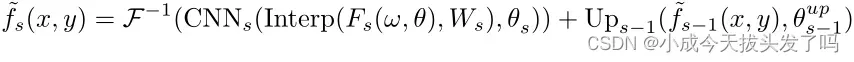
其中，表示具有可学习权重
的校正网络，Interp表示具有可学习权重
的插值算子，
表示s尺度下的输入，
表示s尺度下的输出，
表示具有可学习参数
的从低分辨率图像到高分辨率图像的上采样层。重建的图像
被定义为最高分辨率
中的估计。在实现中，我们将S设置为4，并且
。示意图见图2。设
表示具有j个训练样本的训练集，其中每个(p^j,f^j)表示一对正弦图和真实图像。通过最小化以下损失函数来训练网络:
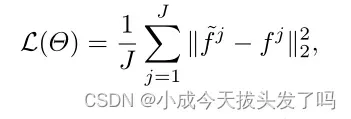
其中，Θ：表示NN的整个参数集。
文章MICCAI_2021_CT_Interp.pdf (cpb-us-w2.wpmucdn.com)
转自知乎的傅里叶分析掐死教程傅里叶分析之掐死教程（完整版）更新于2014.06.06 – 知乎 (zhihu.com)
https://zhuanlan.zhihu.com/p/19763358
转自知乎的从线性空间角度学习傅里叶分析
我理解的傅里叶变换 – 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/23739221
文章出处登录后可见！
