基本优化方法
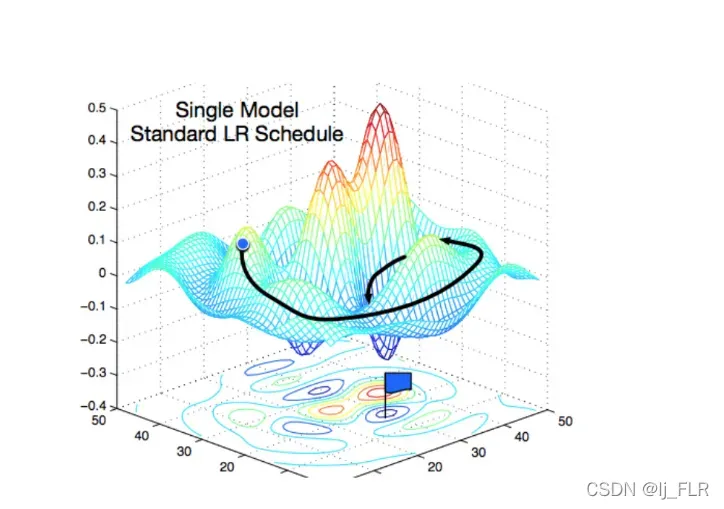
这个图可以直观的看到找到最优解的路线
梯度下降
具有显式解决方案的模型非常简单,但是我们将来要解决的几乎所有问题都没有显式解决方案。
当模型没有显示解决方案时会发生什么?
让我们谈谈梯度下降:
- 梯度下降是通过沿逆梯度方向不断更新参数来解决的
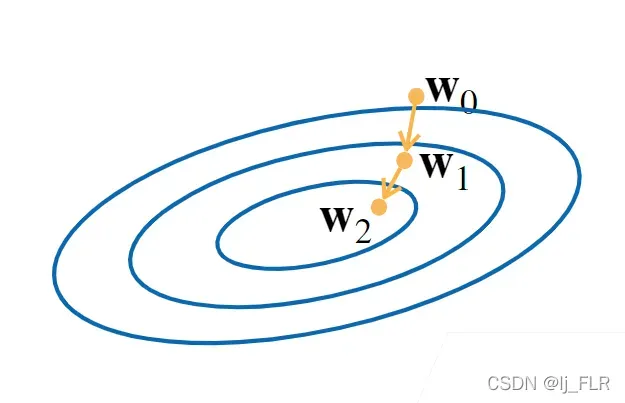
- 挑选一个参数的随机初始值w0
- 重复迭代参数t=1,2,3(在接下来的时刻里不断更新w0,来接近我们的最优解)
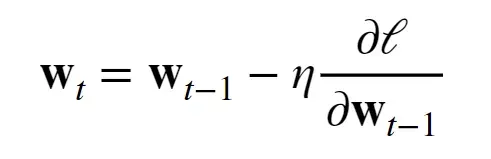
(上图为更新法则,意思是:上一个时刻 减去 学习率(标量)*损失函数关于t-1时刻的梯度) - 沿着梯度方向会增加损失函数值
- 学习率:步长的超参数
然后选择既不太小也不太大的学习率:
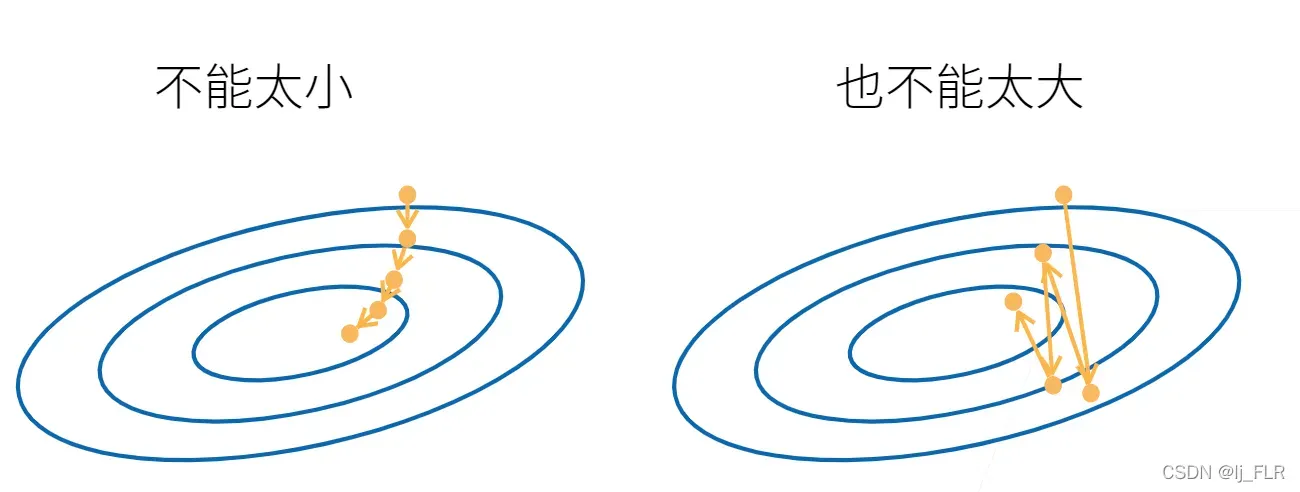
如果太大,就相当于一直在震荡,而不是跌落。
小批量随机梯度下降
小批量随机梯度下降是深度学习的默认解算法
我们经常使用的方法不是梯度下降,而是小批量的随机梯度下降,因为每次计算梯度都需要导出整个损失函数,相当于对梯度计算整个样本一次。 (计算梯度的复杂度与样本数成线性关系)

同样,批量大小不能太大或太小:
- 每次计算量太小,无法并行使用计算资源
- 太大,内存消耗增加,计算浪费(如果所有样本都相同)
文章出处登录后可见!
已经登录?立即刷新
